Adaptive Consensus of Non-Strict Feedback Switched Multi-Agent Systems With Input Saturations

Zhanjie Li and Jun Zhao,

Abstract—This paper considers the leader-following consensus for a class of nonlinear switched multi-agent systems (MASs)with non-strict feedback forms and input saturations under unknown switching mechanisms.First,in virtue of Gaussian error functions,the saturation nonlinearities are represented by asymmetric saturation models.Second,neural networks are utilized to approximate some unknown packaged functions,and the structural property of Gaussian basis functions is introduced to handle the non-strict feedback terms.Third,by using the backstepping process,a common Lyapunov function is constructed for all the subsystems of the followers.At last,we propose an adaptive consensus protocol,under which the tracking error under arbitrary switching converges to a small neighborhood of the origin.The effectiveness of the proposed protocol is illustrated by a simulation example.

I.INTRODUCTION

IN recent years,the topic on the leader-following consensus control of multi-agent systems (MASs)has captured considerable attention [1]–[5].In [6],the leader-following consensus problem was addressed for networked MASs with limited communication resources and unknown-but-bounded noise.In [7],by introducing an auxiliary parameter for each agent,a distributed dynamic event-triggered strategy and a distributed adaptive consensus protocol were proposed to solve the event-triggered consensus of general linear MASs.Leader-following consensus involves many natural phenomena and has wide practical applications,such as the migration of birds and formation control for mobile robots.In the existing results,a large amount of effort has been put into the consensus problem of linear or nonlinear MASs with matching conditions [8]–[10].

When the agents involve mismatching nonlinear uncertainties,however,the approaches mentioned above cannot be used to achieve consensus of MASs.To this end,adaptive neural/fuzzy strategies have been proposed by using the approximation capability to unknown functions [11]–[15].With the usage of the backstepping method,the neural networks (NNs)based results concerning the consensus control have been well reported for the strict feedback uncertain MASs,see,for example,[16]–[18].But,for MASs with non-strict feedback forms,the above approaches are inapplicable.The challenge lies in the well-known algebraic loop issue,which will break the backstepping process.Thus,we need new control schemes to handle the non-strict feedback terms.In [19]–[21],by utilizing the structural property of the Gaussian basis function,the consensus tracking problems were studied for nonlinear MASs subjected to non-strict feedback terms.However,the results [16]–[21]are obtained just for MASs whose followers are modeled by single dynamics.The multiple dynamics behaviors are very common in engineering applications,such as the continuously stirred tank reactor system [22] and the two inverted pendulums system [23].Thus,it is important to propose a proper consensus protocol for more general MASs with multiple dynamics.

Switched systems provide a more general framework to describe the multiple dynamics behavior of processes[24]–[29].Switched systems have an important feature that they do not essentially inherit the behavior of their subsystems[30]–[32].For example,some switching laws can destabilize a switched system with all stable subsystems [33]–[35].Thus,when the switching mechanisms are unknown,we should deal with all possible switching mechanisms to achieve the consensus of MASs,which implies a common Lyapunov function (CLF)for all subsystems of the agents.In [36],[37],a CLF was constructed to achieve the consensus tracking of switched MASs with strict and pure-strict feedback forms,respectively.It is stressed that the leader-followering consensus of MASs with non-strict feedback forms is not fully taken into account.This is mainly due to the fact that in the iterative design process,each agent is associated with not only its spilled variables but also state variables of its neighbours.These undesired extra states make it difficult to proceed to the iterative process.On the other hand,input saturation is inevitable in many real life dynamical plants due to the physical limitation of the actuator [38]–[42].However,due to the interactions among unknown switching mechanisms,nonstrict feedback terms and input saturations,the adaptive leader-follower consensus for switched MASs with non-strict feedback terms and input saturation has not been clearly studied.

In this paper,we will focus on the consensus tracking control for a class of nonlinear switched MASs with non-strict feedback forms and input saturation under unknown switching mechanisms.The main work is summarized as follows.1)This paper makes the first attempt to the adaptive leaderfollowing consensus for the uncertain switched MASs with non-strict feedback terms and input saturations.The studied MASs have a more general structure and can reduce to some special case of non-switched MASs or switched MASs with strict-feedback terms.2)The nonlinear terms of the followers are unknown and have the non-strict feedback forms.In virtue of the NNs approximation and the structural feature of Gaussian basis functions,the unknown nonlinear terms are compensated and the algebraic loop problem caused by undesired extra states is solved.3)All the subsystems of each follower are allowed to have switched dynamics.We construct a CLF for all the associated subsystems,which allows the switching mechanisms to be arbitrary and unknown.Besides,the saturation nonlinearities are represented by asymmetric saturation models.An appropriate consensus protocol is proposed to ensure the tracking performance in presence of input saturation.

The used notation of this paper is standard.Denote byRnand Rn×mthe realn-vector space andn×m-matrix space,respectively.For a scalarx1,|x1| is its absolute value.For a vectorx,is the Euclidean norm withxTbeing its transpose.Let λmin(A)be the minimum singular value of a matrixA.diag(b1,...,bn) denotes ann×ndiagonal matrix whose element (i,i) isbi.s ign(·)denotes the sign function.

II.PROBLEM STATEMENT AND PRELIMINARIES

A.Problem Statement

Consider a nonlinear MAS which consists ofNfollowers and one leader.The leader output is a desired reference signalye,and the dynamics of thej-th follower are given by

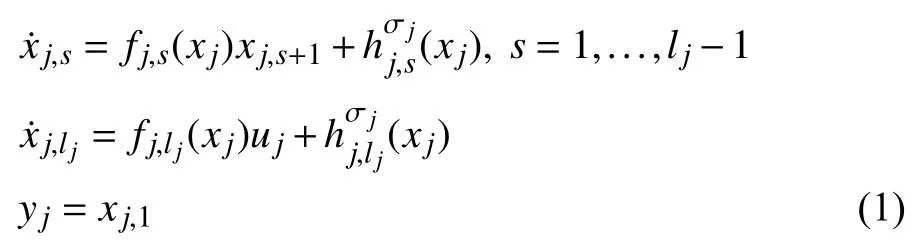
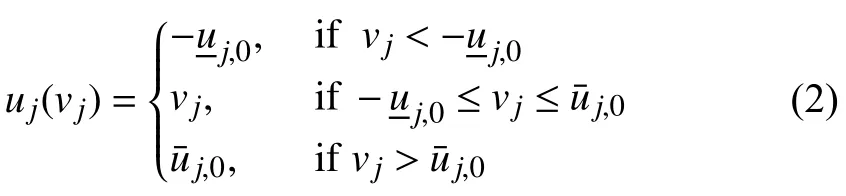
Remark 1:The MAS (1)is a switched system in which each follower switches among different dynamics.WhenM0={1},the uncertain nonlinear termof the MAS (1)reduces to that of non-switched MASs considered in [20],[21],[39].In addition,compared with the switched MASs in [36],[37]where the nonlinear functions are in the strict and pure-strict feedback forms,respectively,the MAS (1)contains the nonstrict feedback termwhich is associated with the whole state variables.Thus,the MAS (1)has a more general structure.

The objective of this paper is to explore an adaptive protocol for each follower in (1)such that for the desired leader signalyeand a small constant >0,the consensus tracking errorej=yj−yesatisfies limt→∞|ej(t)|≤ϱ,j=1,2,...,N,that is,e=(e1,e2,...,eN)Tconverges to a small neighbourhood near the origin.

Before deriving a solution to this consensus objective,some necessary preliminaries and assumptions are presented,and some useful lemmas are introduced.

B.Communication Graph

A directed graphG=(V,E,A)is introduced to express the information transfer between agents.In an MAS,V={V1,V2,...,VN}denotes the set of agents (or nodes),E⊆V×Vdenotes the set of directed edges andA=[ai,j]∈RN×Nis the adjacency matrix.EdgeEj,i=(Vj,Vi)∈Emeans the information flow from agentjto agenti.In matrixA,ai,j>0 indicates the weight of this edge,otherwise,ai,j=0.In our context,we do not consider the self-loop,thus,ai,i=0.Denote byL=D−Athe Laplacian matrix,in whichD=diag{d1,...,dN}∈RN×Nis the in-degree matrix with.The neighbor setNi={Vj|(Vj,Vi)∈E} contains all neighbors of the agenti.A graph has a directed spanning tree if there is a node named root,which has a directed path to the rest of nodes.The augmented graphofGis used when considering the leader,whereis the node set involving the leader,anddenotes the edge set of.The leader adjacency matrix is defined byB=diag{b1,...,bN},wherebi>0 if followerican get information flow from the leader,otherwise,bi=0.

Assumption 1:If the leader is considered as the root,the graphhas a directed spanning tree.

Denote the neighbourhood synchronization error as

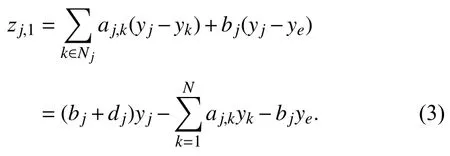
Under Assumption 1,[43] has indicated thatL+Bis nonsingular.Then,we have the following lemma.

Lemma 1 [43]:Denotez=(z1,1,z2,1,...,zN,1)T.Then,the overall consensus tracking errore=(e1,e2,...,eN)Tsatisfies

For the consensus design of MASs,Assumption 1 is standard and commonly used,see for example [21],[39],[43].Using Lemma 1,our control objective can be boiled down to designing the adaptive consensus protocol to make the neighbourhood synchronisation errorz=(z1,1,z2,1,...,zN,1)Tbounded and small.

C.Saturation Nonlinearity

In this context,we adopt a new model,rather than saturation model (2),to describe the saturation nonlinearity.This is mainly due to the fact that in (2),there exist the sharp corners for the relationship betweenvj(t)anduj(t) whenvj=andvj=.The new smooth model is given as in [41]

The function erf(·)is called the Gaussian error function and is smooth.In Fig.1,by taking=3,=4 andv1(t)=10sin(t),we show the evolutions of the saturation models (2)and (5)of the first follower.

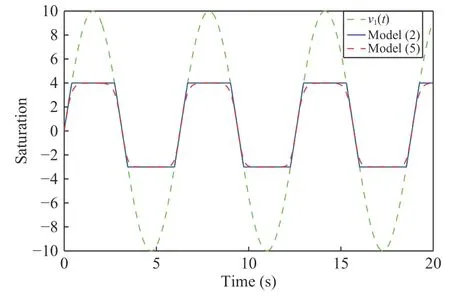
Fig.1.Saturation models (2)and (5).

For thej-th follower,we define the function ∆j(·)as

wheregjis some positive constant.Using the function ∆j(vj),we can rewrite the saturation model (5)as follows:

To design a desired consensus protocol,the following assumption is required.

Assumption 2:There are constants ∆j,0>0,>0 and>0 such that ∆j≤∆j,0,.

Remark 2:From (5),each follower has its own saturation level,and the different lower and upper bounds of each saturation level can be adjusted by alternating the valuesand,respectively.If,(5)is a symmetric saturation actuator,otherwise,(5)is an asymmetric one.In Assumption 2,the boundedness of the disturbances is required,which is reasonable.In a real application,the actual control input cannot be infinite,thus,Assumption 2 is practical in reality.Some similar restrictions can be found in[41],[42].

D.Neural Networks

In practice,a control system often involves some nonlinear uncertainties.To design an effective control strategy,we will adopt the radial basis function (RBF)NNs to model the uncertainties.As shown in [12],ifh(χ)is a continuous function defined on a compact set Σχ⊂Rn,then for a pregiven accuracy level τ>0,there is an RBF NN ϖTΨ(χ)such that

where |ε(χ)|≤τ is the approximation error,ϖ=(ϖ1,ϖ2,...,ϖl)T∈Rlis the weight vector withlbeing the neuron number,and Ψ(χ)=(ψ1(χ),ψ2(χ),...,ψl(χ))∈Rlis the basis function vector with ψi(χ)being selected as the Gaussian function

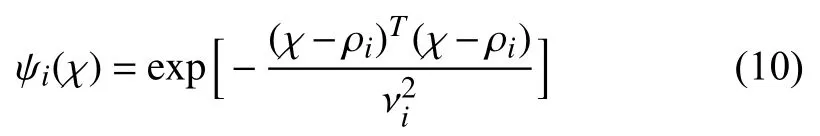
where ρi=(ρ1,ρ2,...,ρn)Tis the center of the receptive field and νiindicates the width of ψi(χ).

In what follows,some lemmas and an assumption are introduced.

Lemma 2 [19]:It is assumed thatis the basis function vector of an RBF NN andis the input vector.For any integersq≥p≥1,the following inequality holds

Lemma 3 [14]:For all (a,b)∈R2,constants ε >0 andp>1,q>1 satisfyingp+q=pq,it holds

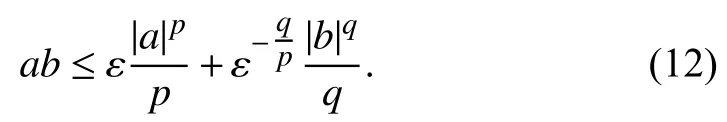
Lemma 4 [13]:Consider a system=−γϑ+s(t).If γ is a positive constant ands(t)is a positive function,then,for all ϑ(t0)≥0,it holds ϑ(t)≥0,∀t≥t0.

Assumption 3:The signalye(t)and its derivatives up toare continuous and bounded withL=max{l1,l2,...,lN}.It is assumed that there is a positive constanty0such that,forj=1,2,...,L.

Lemma 2 shows the property of the Gaussian basis functions of RBF NNs and is useful to apply backstepping for the system with non-strict feedback forms.Young’s inequality in Lemma 3 is used to handle some important inequalities.Lemma 4 is applied to guarantee that all adaptive signals are positive.

III.MAIN RESULT

In this section,we will design the adaptive consensus tracking protocol and construct a CLF for the MAS (1).Then,an analysis procedure will be presented to give the main result.

A.Design of Consensus Protocol

In this subsection,the backstepping method is used to design the desired protocol.The design process involvesljsteps for thej-th follower,and at each step we will use the NNs to approximate the uncertain functions.

For thej-th follower,we introduce a new set of coordinateszj,s,s=1,2,...,lj.The coordinatezj,1is defined in (3)and

We now present the design process.

Step 1:By the definition ofzj,1in (3)and along thei-th subsystem of thej-th follower,one can deduce from (1)that

Choose the Lyapunov function candidate as

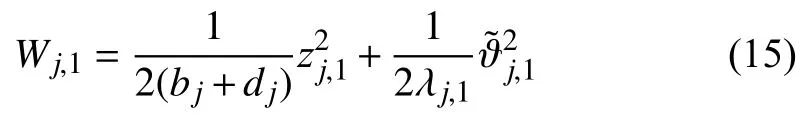
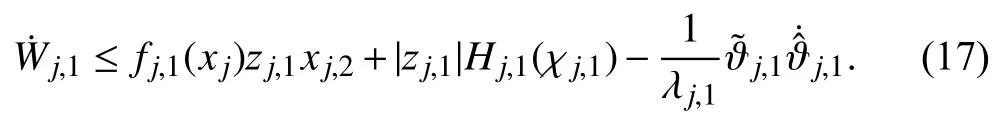
Since the functionHj,1(χj,1)is related to the unknown functionsand,we cannot directly useHj,1(χj,1)to design the desired virtual protocol.To this end,an RBF NN is utilized to approximateHj,1(χj,1)on a compactsuch that for any given τj,1>0,

where εj,1(χj,1)denotes the approximation error satisfying|εj,1(χj,1)|≤τj,1.Applying (18)and Lemmas 2–3,one has

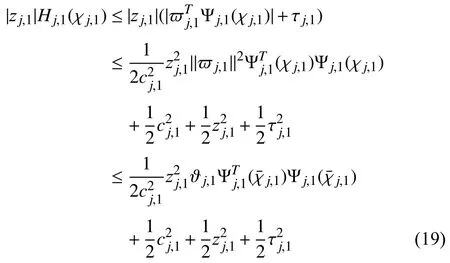
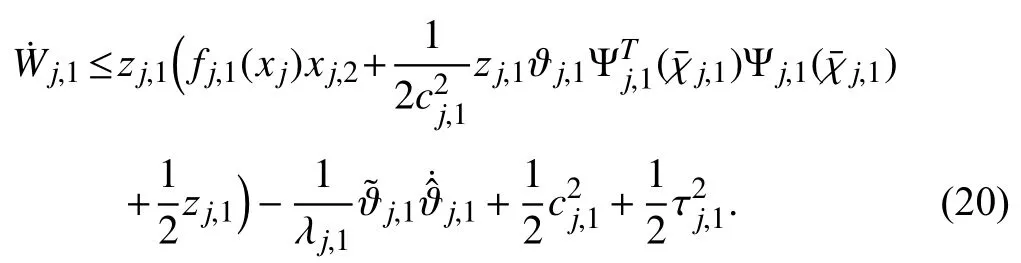
Next,we construct the desired virtual protocoland the adaptive lawas

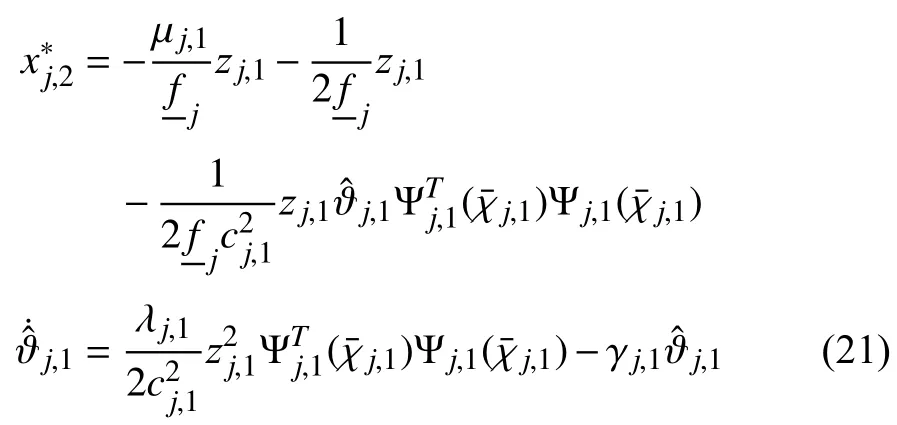
where the constants µj,1,λj,1and γj,1are positive design parameters.By (20)and (21)one deduces that

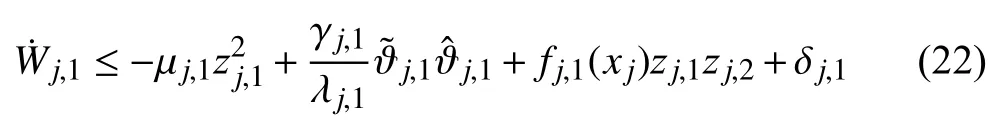
Step s(2≤s≤lj−1):Denote for convenience=0.Suppose that at the first (s−1)-th step,we have designed a set of desired stabilizing functions,m=2,...,s,which are dependent onwithand,the adaptive laws,and a Lyapunov function candidateWj,s−1,such that

where δj,s−1is a constant.In what follows,we will prove that a similar inequality in the form of (23)holds at the stepsfor the following Lyapunov function candidate

By (1)and (13),along thei-th subsystem of thej-th follower,one has

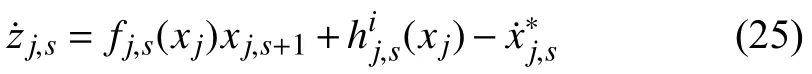
where

In view of (23),the derivative ofWj,salong thei-th subsystem satisfies

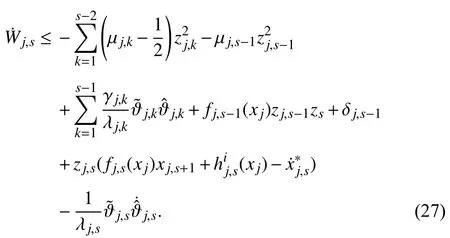
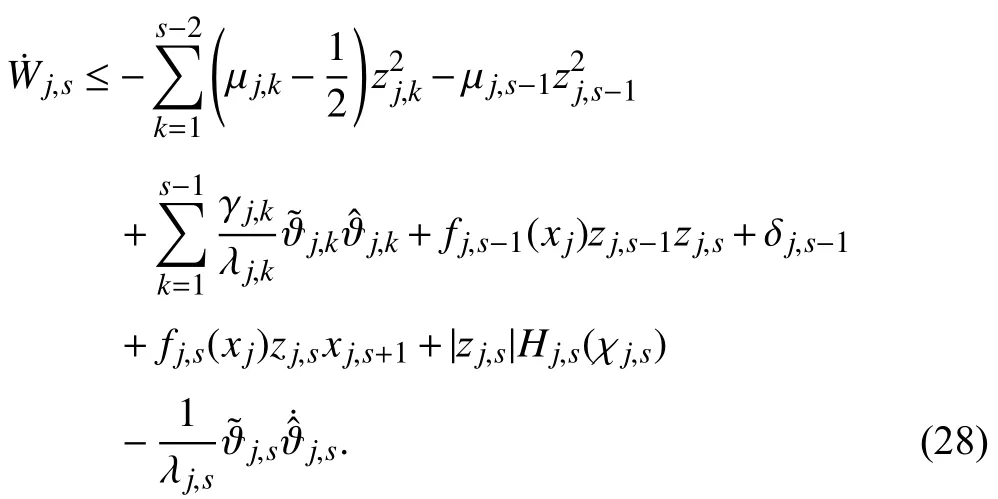
Since the functionHj,s(χj,s)is related to the unknown functionsand,an RBF NN is utilized to approximateHj,s(χj,s) on a compactsuch that for any given τj,s>0,

where εj,s(χj,s)denotes the approximation error satisfying|εj,s(χj,s)|≤τj,s.Applying (29)and Lemmas 2–3,one has

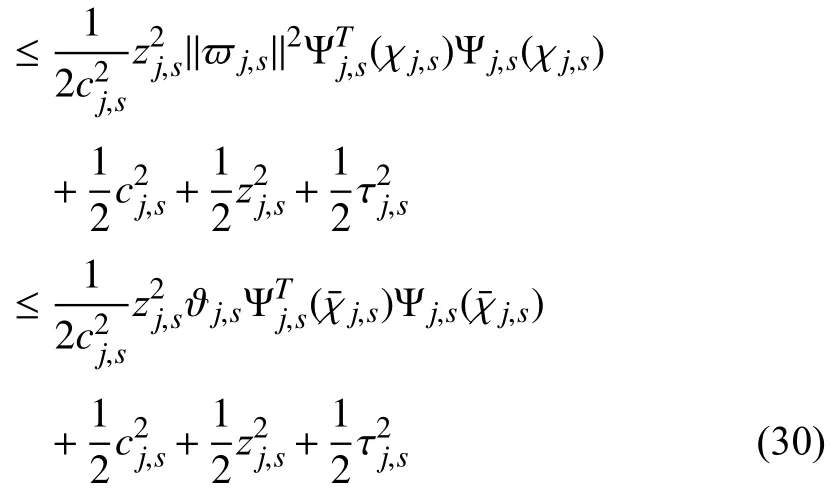
where the constants µj,s,λj,sand γj,sare positive design parameters.Using (28),(30)and (31),one arrives at

Steplj:At the finial step,we consider the Lyapunov function candidate as

By (1)and (13),along thei-th subsystem,one has

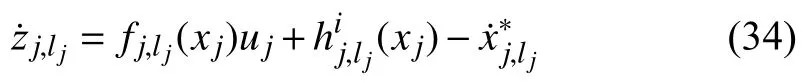
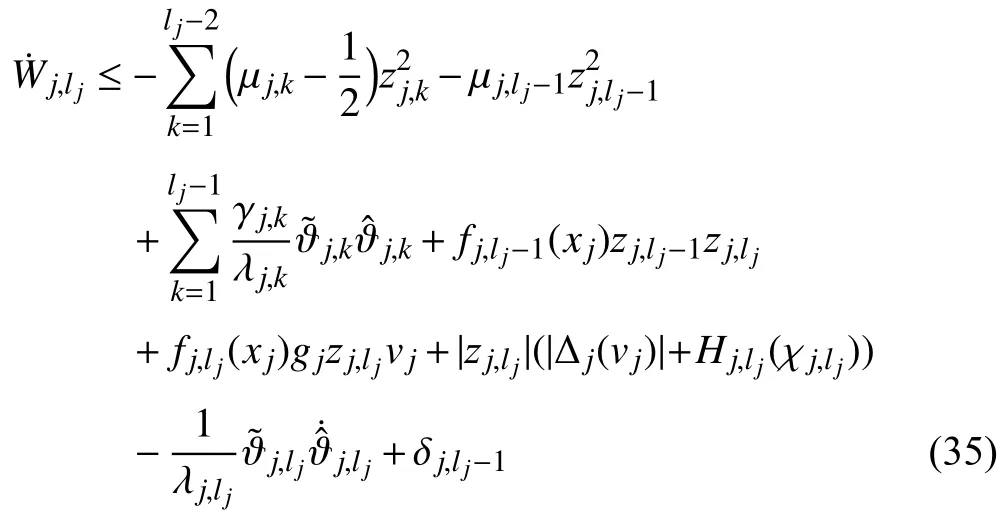
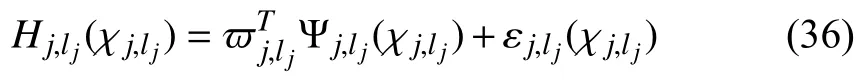
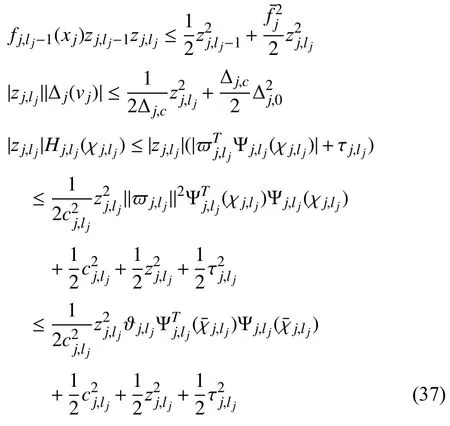
where ∆j,c>0,>0 are design parameters.We construct the actual protocolvjand the adaptive law as

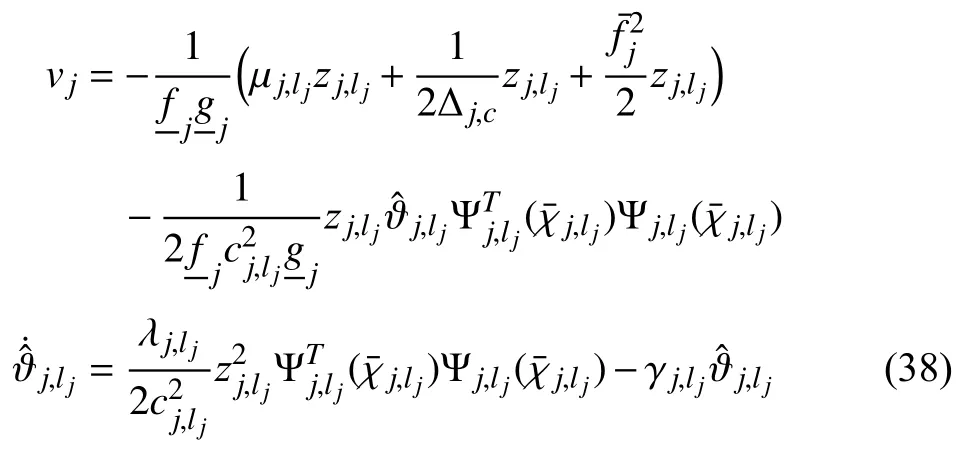
Substituting (37)–(39)into (35)produces

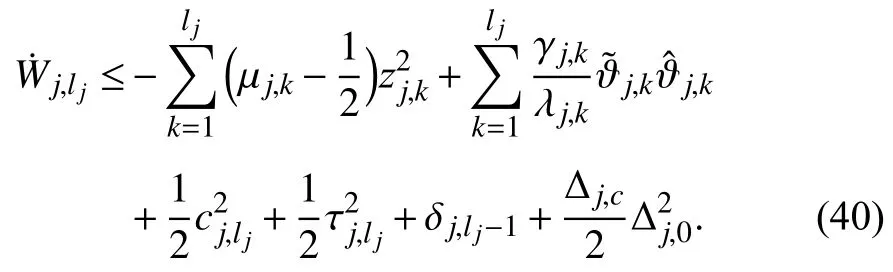
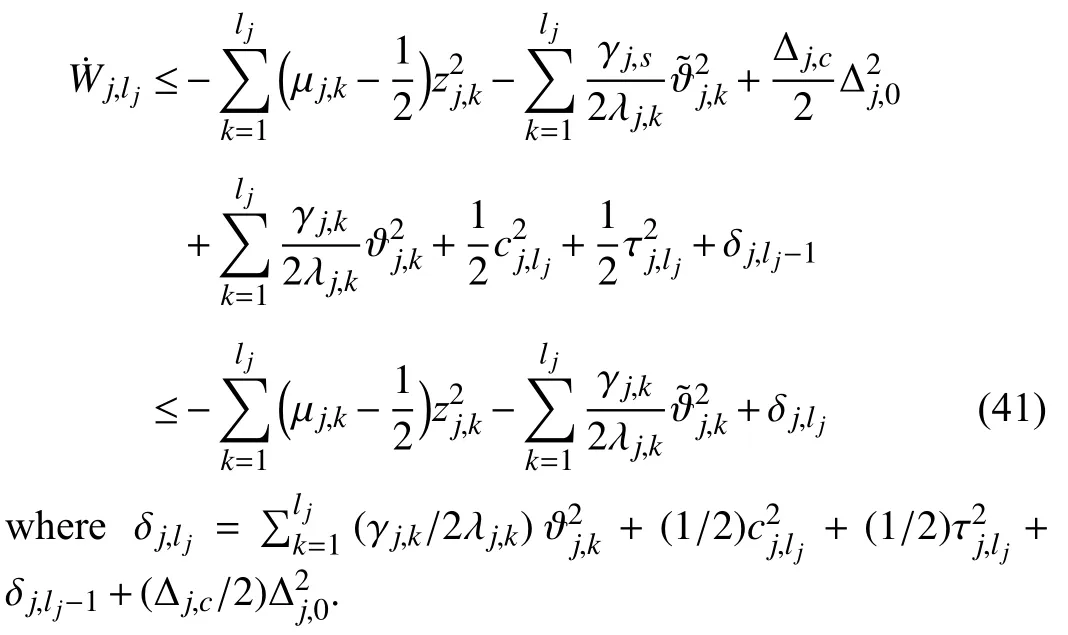
B.Consensus Analysis

In this subsection,we present the main result.

Theorem 1:Consider the switched MAS (1)under Assumptions 1–3,and design the consensus protocol (38),related to the virtual protocols and the adaptive laws (21)and(31),with the designed parameters µj,s>1/2,cj,s>0,∆j,c>0,cj,s>0,τj,s>0 and γj,s>0,j=1,...,N,s=1,...,lj.Let δ=andwith=µj,k−1/2.Then,for the bounded initial conditions,all the closed-loop signals under arbitrary switching are bounded,and the consensus tracking error tends to a small neighbourhood near the origin and satisfies,j=1,2,...,N.

Proof:Choose a common Lyapunov function of the MAS(1)asW=.From (41),it follows that

According to the definitions of δ and µ,we can rewrite (42)as

By (43),we derive that

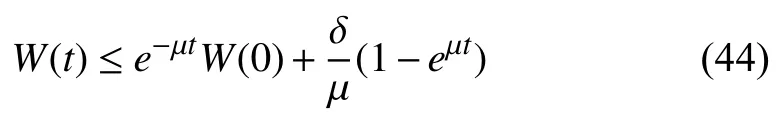
whereW(t)stands forW(z1(t),...,zN(t),.From(44)and the definition ofW,it can be obtained that all the closed-loop signals are bounded under arbitrary switching.In addition,using (44),we can also achieve that

Hence,the following relationship holds

Recalling Lemma 1,we arrive at

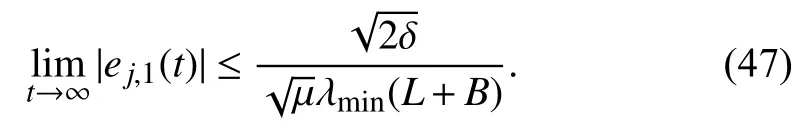
For any constant ϱ>0,we can choose appropriate design parameters such that,which implies that the consensus tracking errors |ej,1(t)| can be made small enough. ■

Remark 3:For the switched MAS (1),how to construct a CLF candidate is rather difficult due to the interaction among switching subsystems,non-strict feedback terms and input saturation.In the iterative design process,at steps,thej-th agent is associated with not only its spilled variablesbut also state variablesxkof its neighbours.The extra undesired variables often destroy the solvability of virtual controllers.To this end,the structural feature of Gaussian basis functions is utilized to eliminate the effect of these undesired variables.

Remark 4:According to the definitions of µ and δ,the satisfactory leader-following consensus performance can be achieved by decreasingcj,s,τj,s,∆j,cand increasing µj,s,γj,s.But,in such a way,a high gain of the designed protocol will be caused.Thus,in practice,the trade-off between desired performance and the protocol gain can be used to guide the choice of design parameters.

IV.AN ILLUSTRATIvE EXAMpLE

In this section,we give an example to illustrate the effectiveness of the designed protocol.

Example 1:Consider a switched MAS composed of three followers and one leader.Fig.2 shows the communication graph,and the dynamics of each follower are described by

wherej=1,2,3,σj:[0,∞)→M0={1,2}.The functionshj,s(xj)=1,j,s=1,2,3.The nonlinear termsand,i∈1,2,have the following form=0.1xj,2xj,3,.The leader output is selected asye=sin(t).The saturation lower and upper bounds are=50,=70,=800,=800,=1200,=1500.

Following the process of Section III,the consensus protocol and the adaptive laws are designed as

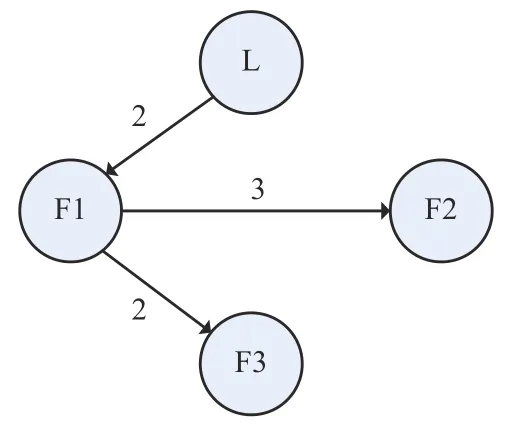
Fig.2.Communication graph between leader and agents.

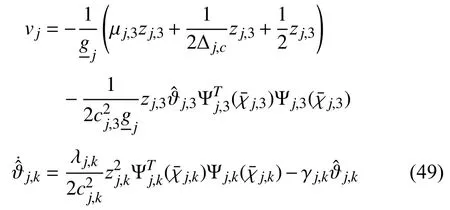
wherej=1,2,3,k=1,2,3,z1,1=2(y1−ye),z2,1=3(y2−y1),z3,1=2(y3−y1),zj,2=xj,2−,zj,3=xj,3−withandbeing defined by (21)and (31),,and forj=2,3,,where.

The parameters are selected as µ1,1=4,µ1,2=15,µ1,3=30,c1,k=0.5,λ1,k=5,γ1,k=3,k=1,2,3,µ2,1=4,µ2,2=10,µ2,3=25,c2,k=0.5,λ2,k=6,γ2,k=3,k=1,2,3,µ3,1=6,µ3,2=20,µ3,3=30,c3,k=0.5,λ3,k=6,γ3,k=4,k=1,2,3,=1,∆j,c=1,j=1,2,3.=30,=50,=100,=200.The initial states are taken as(x1,1(0),x1,2(0),x1,3(0))=(0,0.2,0.1),(x2,1(0),x2,2(0),x2,3(0))=(0.3,−0.1,0.1),(x3,1(0),x3,2(0),x3,3(0))=(−0.2,0,0),and,i=1,2,3,j=2,3.In the sequel,we take the RBF NNs including 16 neurons,and their centers evenly space in [–3,3] and their widths are equal to 5.

Figs.3–7 show the simulation results.Fig.3 depicts switching signals σ1(t),σ2(t)and σ3(t).Fig.4 shows the consensus errors of the followers and the leader.Figs.5–7 demonstrates the responses of the statesxi,j,i,j=1,2,3 and the adaptive laws=1,2,3.From Figs.4–7,it follows that all the closed-loop system signals are bounded under the chosen switching signals,and from Fig.4,it can be clearly seen that all outputs of the followers track that of leader successfully.Besides,in this example,the real errors satisfy|ej(t)|≤0.02,j=1,2,3.The simulation time ist=1.26 s.

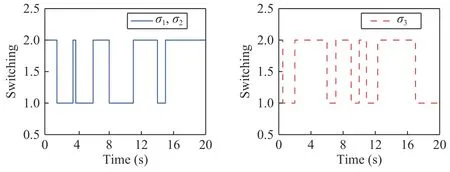
Fig.3.The evolution of switching laws σ1,σ2,σ3.

Example 2:We consider three groups of single-link robot manipulators subjected to nonlinear disturbances.Each system is modeled as=−(1/2)mjljgsin(qj)+uj,where the physical meanings and the values of the system parameters can be founded in [44].Due to the potential changes of system dynamics,we introduce the switching disturbances.By takingxj,1=qjandxj,2=,j=1,2,3,the system model can be rewritten as

Fig.4.The consensus errors between the three followers and the leader.

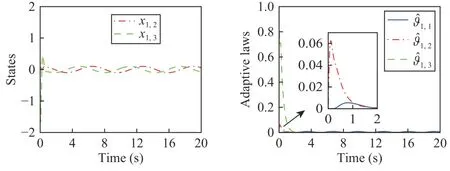
Fig.5.The states and adaptive laws of the follower 1.

Fig.6.The states and adaptive laws of the follower 2.

Fig.7.The states and adaptive laws of the follower 3.

wherej=1,2,3,σj:[0,∞)→M0={1,2},and,,i∈M0,denote the switching disturbances.The communication graph and the switching laws are chosen as in Figs.2 and 3,respectively.The adaptive consensus protocol is designed as in Section III.

Fig.8.The consensus errors in Example 2.

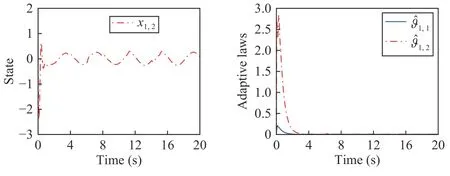
Fig.9.The state and adaptive laws of the follower 1 in Example 2.

Fig.10.The state and adaptive laws of the follower 2 in Example 2.

Fig.11.The states and adaptive laws of the follower 3 in Example 2.

V.CONCLUSIONS

In this paper,an adaptive consensus protocol has been proposed for a class of nonlinear switched MASs with nonstrict feedback forms and input saturations.By utilizing the Gaussian error functions and NNs approximation,the unknown nonlinear terms are compensated,and by constructing a CLF for all the followers,we make the tracking error convergent under arbitrary switching.An interesting problem worthy of further investigation is to extend the developed control strategy to the output feedback design based on an observer.Recent results on cyber deception attacks have been achieved,see e.g.[45]–[47],thus,a problem is whether some results can be obtained for non-strict feedback switched MASs with input saturation under deception attacks.