Static Force-Based Modeling and Parameter Estimation for a Deformable Link Composed of Passive Spherical Joints With Preload Forces

Gaofeng Li,Dezhen Song,Lei Sun,Shan Xu,Hongpeng Wang,and Jingtai Liu

Abstract—To balance the contradiction between higher flexibility and heavier load bearing capacity,we present a novel deformable manipulator which is composed of active rigid joints and deformable links.The deformable link is composed of passive spherical joints with preload forces between socket-ball surfaces.To estimate the load bearing capacity of a deformable link,we present a static force-based model of spherical joint with preload force and analyze the static force propagation in the deformable link.This yields an important result that the load bearing capacity of a spherical joint only depends on its radius,preload force,and static friction coefficient.We further develop a parameter estimation method to estimate the product of preload force and static friction coefficient.The experimental results validate our model.80.4% of percentage errors on the maximum payload mass prediction are below 15%.

I.INTRODUCTION

HOME service robots work in unstructured environments with humans at approximity.Hence a low-cost,dexterous,and intrinsically safe manipulator is necessary.

Traditionally,the links of manipulator are designed to be stiff to avoid kinematic error [1],[2].However,stiff links result in fixed workspace and make it difficult to adapt to various tasks in home service.Moreover,rigid manipulators may cause safety issues by collisions.

Continuum manipulators or soft manipulators,such as the octopus-like arms [3]–[5],the elephant trunks [6]–[8],and the concentric tube robots [9]–[11],offer a number of potential advantages over rigid-link manipulators in safe interaction,as well as adapting to uncertain and complex environments.However,most of continuum manipulators have shortages in strength to manipulate relatively heavy objects.

Here we present a novel low-cost deformable manipulator,which is composed of 4 active rigid joints and 2 deformable links (See Fig.1).The first deformable link connects robot shoulder and elbow.The second deformable link connects robot elbow and wrist.There are 2 active rigid joints in the shoulder and 1 active rigid joint each on the elbow and wrist.The deformable link is a series of passive spherical joints connected with each other,with preload forces between socket-ball surfaces.When external torque is smaller than a threshold,each component of the deformable link is held together due to friction.On the other hand,the spherical joint starts to slip when external torque exceeds the limit.One example of such material is the adjustable elastic cooling tube used in numerical lathe.It is very low-cost and easy to obtain.Besides,the deformable links are compliant with impedance.Therefore,it is intrinsically safe and does not cause serious damage to people and environments.

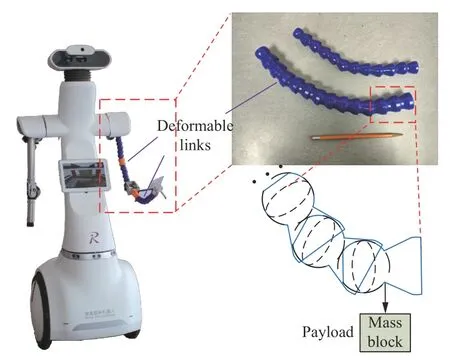
Fig.1.The deformable manipulator deployed on a home service robot and its deformable links.The deformable links are composed of passive spherical joints with preload forces between socket-ball surfaces.One important problem is to estimate the load bearing capacity of the deformable link.

As reported in our previous work [12]–[14],the major benefit of the deformable manipulator is that its workspace can be adjusted by bending its deformable links according to different tasks.Thus,the deformable manipulator can reach more parts of the task spaces with fewer joints.For example,suppose there are two task spaces in front of the robot,one is horizontal and the other is vertical.The working space of rigid-link manipulator is fixed.In contrast,the working space of deformable manipulator can be adjusted by bending its deformable links.Compared with the traditional manipulator,the deformable one can have more intersections with task spaces.At the same time,it can bear heavier payload than the soft manipulator by choosing a proper preload force.

In previous work,the kinematic-free control problem of deformable manipulators is studied [13],[14].It is important to analyze the static force between the deformable links:1)It is necessary to estimate the load bearing capacity of the deformable link in different configurations.2)It fundamentally facilitates automatic bending operation.To achieve the extended workspace,it is desired to control the active rigid joints to overcome friction forces in these spherical joints and bend the deformable links as needed.In both cases,the accurate frictional moment prediction is necessary.

Though a lot of models that consider clearance or lubrication in spherical joints have been proposed,the spherical joint with a preload force between socket-ball surfaces has not been studied.The goal of existing models is to eliminate the impacts of friction,which can seriously degrade the performance of a multi-body system.However,the friction caused by preload force has a positive contribution to load bearing capacity.Just because of the preload force,each component of the deformable link is locked together and can bear heavier payload.Therefore it is important to model the spherical joint with preload force and analyze the frictional moments in these joints.

Our contributions are summarized as follows.

1)We introduce a novel deformable link for deformable manipulators to balance the contradiction between higher flexibility and heavier load bearing capacity.The deformable link is a series of passive spherical joints connected with each other,with preload forces between socket-ball surfaces.

2)We present a static force-based model of spherical joints with preload forces and analyze the static force propagation in the deformable link.This yields an important result that the load bearing capacity of a spherical joint only depends on its radius,preload force and static friction coefficient.The preload force and static friction coefficient are always shown in the form of their product.

3)We propose a low-cost parameter estimation method to estimate the product of preload force and static friction coefficient.

II.RELATED WORk

Our work relates to continuum manipulators.Compared with rigid-link manipulators,continuum flexible manipulators are capable of adapting to uncertain and complex environments.The robot with octopus-like arms can swim like a real octopus underwater [3]–[5].The elephant trunks inspired by elephant are particularly useful for working in obstacle-filled environments [6]–[8].The concentric tube robots have found successful application in minimally invasive surgery [9]–[11].The tendon-driven robots work well in the constrained environments [15],[16].These manipulators have realized high flexibility.However,their lacks of strength make it difficult for them to manipulate heavy payloads.

There is still little related work in considering the load bearing capacity of continuum manipulators.Chenget al.[17] design a cable-driven tunable-stiffness soft manipulator using jamming of granular media.They gain the payload from 8 0 g to 740 g.Jianget al.[18] introduce a manipulator with honeycomb pneumatic network (HPN)structure that can exhibit a load of 2.8 N at a 63 cm distance.However,these manipulators are generally bulky in comparison to their strength.Sturges and Laowattana [19] design a central tendon locking spine which consists of a set of cylindrical beads strung on a flexible cable.By pulling and relaxing the cable tension,the stiffness of the spine is controllable.However,the load bearing capacity of such design is not analyzed.Furthermore,enlargement of this mechanism to realize an application in home service is difficult.Rohet al.[20],[21] propose a wire-reduction mechanism to amplify the load bearing capacity of a flexible surgical instrument.However,the design of the wire-reduction mechanism is complex and the high cost of this mechanism makes it difficult to be applied in home service.

Another group of related work is the spherical joint.A lot of models are proposed for spherical joints with clearance or lubrication to eliminate impacts of friction.In [22],the nonlinear stiffness of spherical joints with small clearance is investigated based on the Winkler model and geometric constraints.An improved dynamic model by utilizing the decoupled natural orthogonal complement (DeNOC)matrices is presented in [23] for a multi-body system with spherical joints.Floreset al.[24] present a contact force model to access the influence of spherical clearance joints.Faraz and Payandeh[25] present two approximate models for both revolute joints and spherical socket-ball joints to analyze the frictional moment in these joints.Uguz and Oka [26] model the effects of mechanical load to predict the fatigue life of a ball joint.

Though there are many existing works on spherical joints,the preload force between socket-ball surfaces has never been considered.In the above models,the contact between socket and ball is point contact or Hertz contact [27].The friction can seriously degrade the performance of a multi-body system.Therefore,the goal of these models is to eliminate the impacts of friction by considering clearance or lubrication between socket-ball surfaces.However,the socket and ball are attached tightly in our case,due to the existence of preload force.The external payload causes the change of stress distribution instead of contact area.In the following sections,we will analyze the quantitative relation between the load bearing capacity and the preload force.

III.PROBLEM STATEMENT

A.Performance Metric for Load Bearing Capacity

The intuitive metric for the load bearing capacity is the weight of payload it can hold without causing slip.However,the payload weight that a spherical joint can hold is closely related to the position and direction it is applied on.In this work,we choose the load moment as an index for the load bearing capacity.To facilitate our analysis,we give the following definitions:

Definition 1:The Tolerated Moment Set of a spherical jointis a set of load moments that cause no slip of the spherical joint.We choose the maximum value in the Tolerated Moment Set as theload bearing capacity of the spherical joint.

This definition gives the metric for a single spherical joint.To evaluate the load bearing capacity of a deformable link,the second definition is given:

Definition 2:The Tolerated Moment Set of a deformable linkis a set of load moments that are applied on the tip component of this link and cause no slip of any spherical joints in this link.We choose the maximum value in the Tolerated Moment Set as theload bearing capacity of the deformable link.

To realize comparison among manipulators with various shapes and scales,we need to calculate the load moment relative to the base frame.

When the acting point is fixed and all parts of the link are constrained in a horizontal plane,the payload mass is a more intuitive index for the load bearing capacity.We will explain this further in Section V.

B.Assumptions and Notations

Consider a deformable link composed of spherical joints with preload forces between socket-ball surfaces.Our goal is to analyze the positive contribution of friction to the load bearing capacity.To simply the problem,we make the following assumptions:

Assumption 1:The gravity of each component in the deformable link is negligible.

This assumption is reasonable because the material of the deformable link is light weight1The material is polyoxymethylene..Compared with the external payload,the self-weight of this link is negligible.

Assumption 2:Two adjacent components of the deformable link are connected by a spherical joint with the preload force between socket-ball surfaces.The contact area between socket-ball surfaces can be approximated as a sphere.

Assumption 3:The preload force between socket-ball surfaces can be approximated by an isotropic distribution.Under the external force,the radial stress between socket-ball surfaces has an elliptical distribution (See Fig.2).

Fig.2.The preload force between socket-ball surfaces is isotropic with magnitude δ0.Under the external force,the stress distribution between socketball surfaces is composed of two half-ellipsoids.The two half-ellipsoids share a pair of equal semi-axes with δ0.The third semi-axes,which rotate θ to ,are δ0+δmax and δ0−δmax,respectively.

This assumption is a variant of the classical Hertz contact.In the classical Hertz contact,the external payload cause an elliptical distribution at the contact area.In our case,the stress distribution is the superposition of a spherical isotropic distribution (caused by the preload force)and an elliptical distribution (caused by the external payload).

Assumption 4:The geometry deformation of each component is negligible under the external force.

Let us define the following notations.

{i} The frame {i},which is attached to thei-th component of a deformable link.

SS=is the kinematic chain of the deformable link.∈S E(3)is the transformation matrix between two adjacent components.

FiThe external force exerted on thei-th component by the (i+1)-th component.

ff=∥Fi∥.The magnitude of the external force.

QiQi=[qx,qy,qz]T.The acting point ofFi.

NiThe external moment exerted on thei-th component by the (i+1)-th component.

NimaxThe load bearing capacity of thei-th spherical joint.

NmaxThe load bearing capacity of the deformable link.

RThe radius of the spherical joint.

θ The angle where the maximum radial stress occurs.

δ0The magnitude of the preload force between socketball surface.

δmaxThe maximum increment of the radial stress due to the external force.

µsThe static friction coefficient.

dNiThe normal force on an infinitesimal areaiPof thei-th spherical joint.

fNfN=.The magnitude of the normal force on an infinitesimal area.

fTfT=.The magnitude of the tangential force on an infinitesimal area.

µ µ=fT/fN.The ratio of tangential and normal force.

C.Problem Definition

Our problem can be given as follows:

Problem:Given a deformable link composed ofM−1 sphe{rical joints wi} th the preload force δ0,the kinematic chainS=,the external forceM−1FM−1and its acting pointM−1QM−1on the tip component,estimate the frictional moment,iNi,on each spherical joint,and predict the load bearing capacity,∥Nmax∥,of the deformable link.

IV.STATIC FORCE MODELING

In this part,the kinematic expression of the deformable link is derived first.Then we analyze the static force propagation between the deformable links.Based on the static force-based model of the spherical joint with the preload force,we can predict the load bearing capacity of a spherical joint and a deformable link.We further develop a parameter estimation method to estimate the product of the preload force and the static friction coefficient.

A.Kinematic Expression of the Deformable Link

The deformable link is a series of passive spherical joints connected with each other.The kinematic chain of a deformable link is parameterized byS=.

B.Static Force Propagation

In this paper,the prefixed superscript indicates in which frame a vector is defined.Suppose the forceiFiand the momentiNiexerted on thei-th component by the (i+1)-th component are known.We first analyze how the force and the moment are propagated from thei-th component to the (i−1)-th component.Denoteandas the normal and the tangential forces,respectively,exerted on thei-th component by the (i−1)-th component at pointiP(as shown in Fig.3).According to the force-moment balance relationship,we have

where“ ×”is the cross product of two vectors.

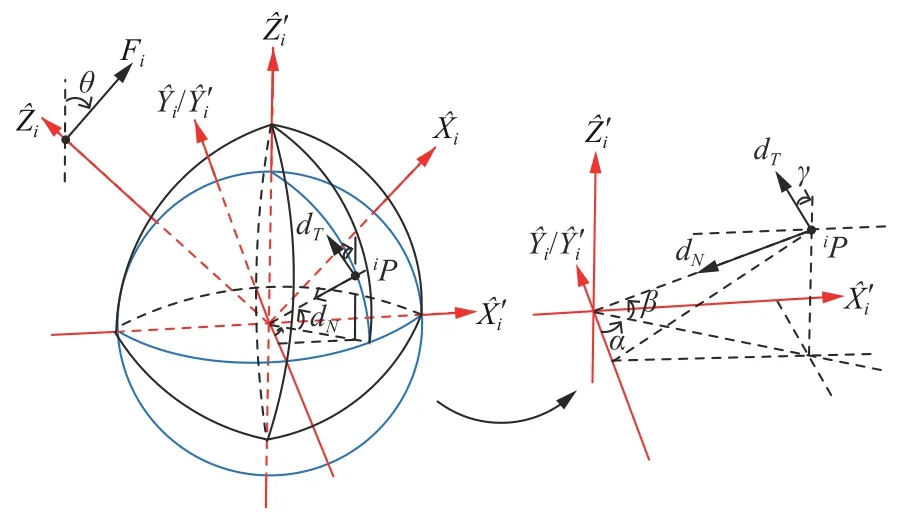
Fig.3.The infinitesimal amount of the normal and the tangential forces exerted on the i -th spherical joint by the (i+1)-th component.The resulting force and the moment are obtained by the integration over the socket-ball surfaces.

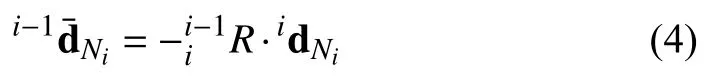
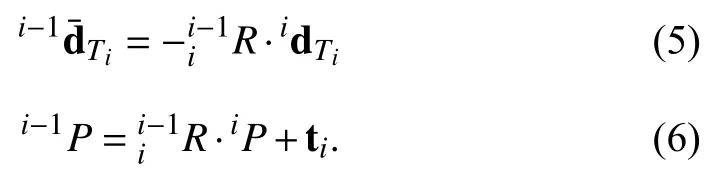
The force and the moment exerted on the (i−1)-th component by thei-th component are obtained by accumulatingandover all pointsiP.Therefore,we have

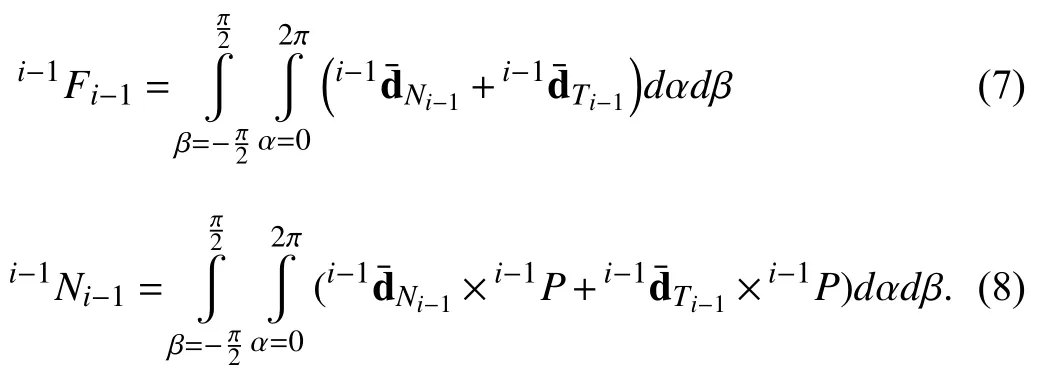
Substituting (2)–(6)into (7)and (8),we can obtain

Therefore we can calculateiNiiteratively whenM−1FM−1andM−1QM−1are given.In the following analysis,we us eiNi(M−1NM−1)to represent the frictional moment on each spherical joint caused byM−1NM−1.

C.Static Force-Based Modeling of Spherical Joint With Preload Force

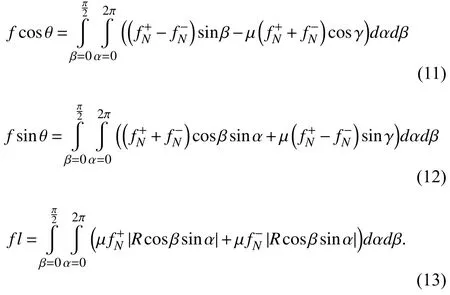
Now let us consider a single spherical joint with the preload force between socket-ball surfaces.Without loss of generality,we assume a representative case that the acting point of the external force isiQ=[0,0,l]Tand the external force isiFi=[f,0,0]T.ForiFiwith any direction and acting point,we can build a new frame,whereis the direction ofiFiandis vertical and intersects withiFi(as shown in Fig.4).Thus it can easily be transferred to the representative case by pre-multiplying a transformation matrix.In the following discussion,we only consider the representative case.

Lemma 1:The load bearing capacity of a spherical joint,∥Nimax∥,depends only on its radiusR,preload force δ0,and static friction coefficient µs.Furthermore,∥Nimax∥ is given by

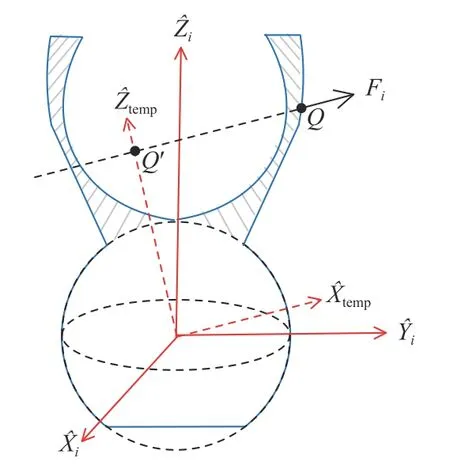
Fig.4.For iFi with any direction and acting point,it can easily be transferred to a representative case that i Fi=[f,0,0]T and i Q=[0,0,l]T.

Proof:To facilitate analysis,we build a new frame(as shown in Fig.3).

Consider the forces acting on an infinitesimal area (Fig.3).According toAssumption 3,the normal force between socketball surfaces is given by

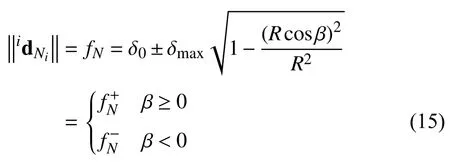
where δmaxis the maximum increment of the radial stress,=δ0+δmaxsinβ,=δ0−δmaxsinβ.

The magnitude of tangential force is given by

where µ is the ratio of the tangential force and the normal force.The direction of tangential force is orthogonal to bothand the normal force.

By integrating over the contact area,equilibrium equations of forces along,and moment aroundcan be written as (11)–(13),where

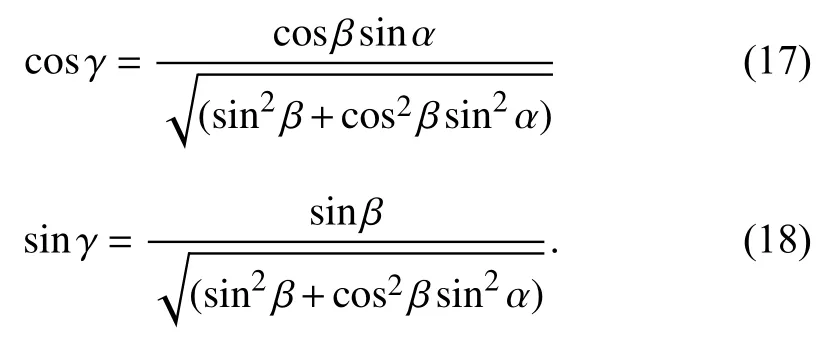
By substituting (17)and (18)into (11)–(13),and computing the integrations,(11)–(13)can be written as

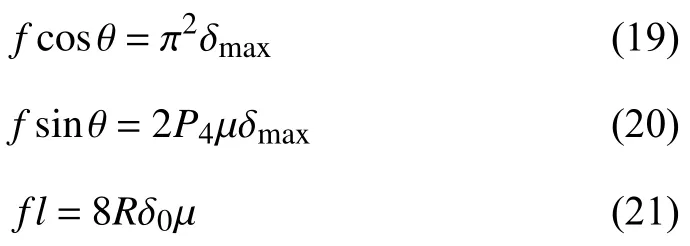
whereP4==5.4397.

Equations (19)–(21)can be solved and we have

When µ>µs,the spherical joint starts to slip.Hence,the load bearing capacity of a spherical joint is obtained whenµ=µs

wherefsandlsare the force and the acting distance,respectively,when µ=µs. ■

Corollary 1:The Tolerated Moment Set of a deformable link is given by

whereRi,δ0i,µsiare the radius,preload force and static friction coefficient,respectively,of thei-th spherical joint.

Corollary 2:The load bearing capacity of a deformable link is given by

Based on Definition 2 and Lemma 1,Corollary 1 and Corollary 2 are straightforward.

Remark 1:According to (25),the load bearing capacity of each joint can be calculated.When the external payload is applied to the distal component,the force and moment is transmitted iteratively from the distal component to the proximal component,according to (9)and (10).Thus,we can predict the load bearing capacity of the deformable link in various configurations.Moreover,we can predict which spherical joint would start to slip firstly.

Remark 2:To realize comparison between different links with different numbers of spherical joints,we need to calculate the load moment relative to the base frame,.

D.Parameter Estimation

In the model described by (22)–(24),µ,θ,δ0,and δmaxare unobservable.fandlare controllable.µ and δ0cannot be calculated separately.However,µ and δ0are always shown in the form of their product,µδ0.Therefore,we can estimate the product of µ and δ0instead of themselves.According to (22),we have

Suppose µsis constant for a specific material.fsis the magnitude of external force when µ=µsat distancels.Equation (21)can be written as

By collecting experimental data,j=1,2,...,we can get a data-fitted curve

Then,we have

V.EXpERIMENTS

In order to validate our model developed in Section IV,a set of experiments are performed for two deformable links composed of spherical joints in different sizes.The material of deformable links is polyoxymethylene.They can be used as the adjustable elastic cooling tube in the numerical lathe.The first deformable link is composed of 8 spherical joints with a smaller radius.The second one is composed of 10 spherical joints with a larger radius.More details about the geometry sizes are shown in Fig.5 and Table I.

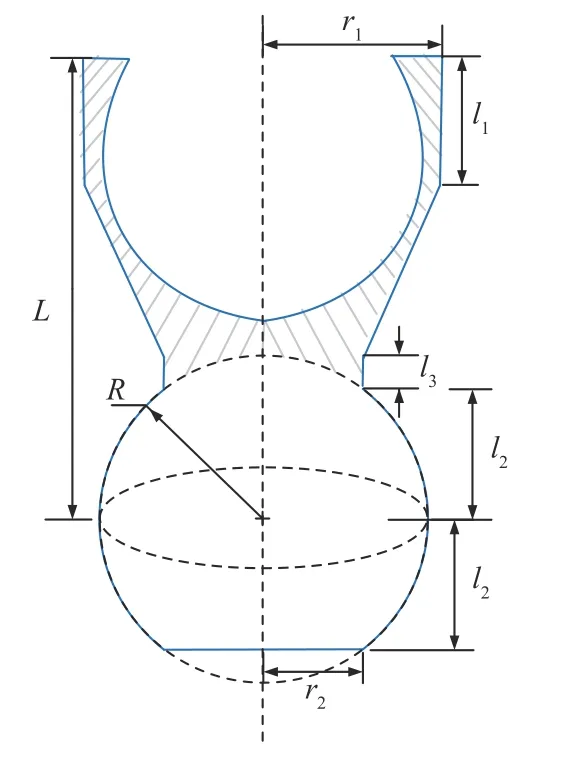
Fig.5.The geometry size of one component of the deformable link.

TABLE I THE GEOMETRY SIzES OF THE TwO DEFORMABLE LINkS

A photo of the experiment setup is shown in Fig.6(a).The base component of the deformable link is fixed on a vise clamp,with payload at the tip component.A 640×480 pixel resolution RGB-D camera (RealSense F200,Intel,USA)is placed on the top of the deformable link to measure its kinematic parameters.A screenshot of the measurement process is shown in Fig.6(b).The blue points are backprojected from each pixel of the depth image taken by the RGB-D camera.The color points are generated according to the current kinematic parameters of the deformable link.

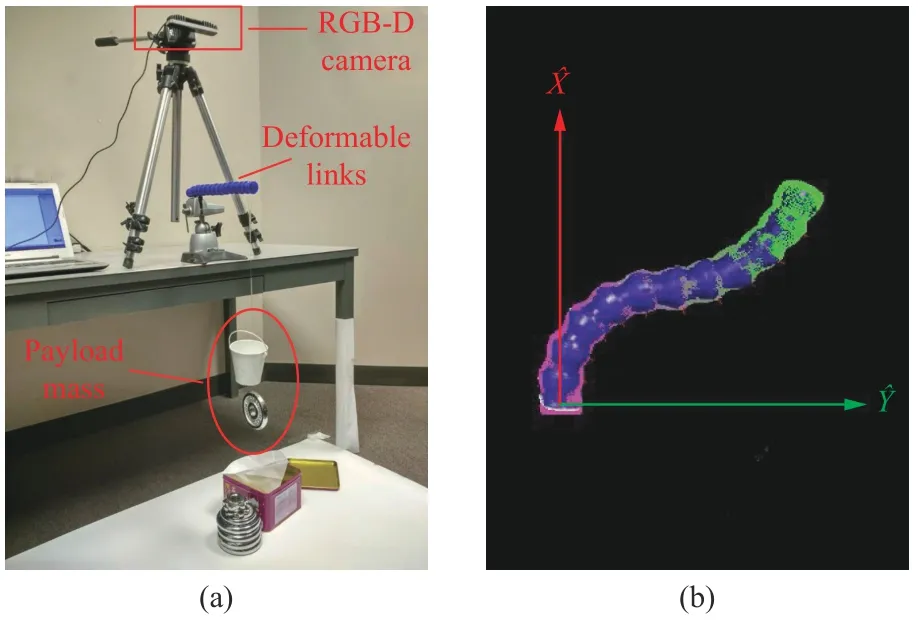
Fig.6.(a)A photo of the experiment setup.The base component of the deformable link is fixed on a vise clamp.An RGB-D camera (RealSense,F200)is placed on the top of the deformable link to measure its kinematic parameters.(b)A screenshot of the measurement process.

Instead of using an expensive force sensor to measurefs,we propose a low-cost experiment scheme by using the weight of payload.The payload is exerted on the tip component by a fishing line.In the following experiments,the deformable links are constrained in a horizontal plane and the acting point is fixed.Consequently,the maximum payload mass is a more intuitive index for the load bearing capacity and easier to measure.By adding/removing rice grains to/from the cup,which is a part of the payload,we can adjust the mass of the payload accurately.

A.Estimation of

In this group of experiments,we first estimate the product of µ and δ0,,for each joint.

We place the spherical joint horizontally.As a result,the-axis of spherical joint is horizontal.The payload is applied at different distanceslsby a fishing line.Then we increase the payload mass gradually until the spherical joint starts to slip.Then we get the maximum payload massms.Equation (30)can be written as

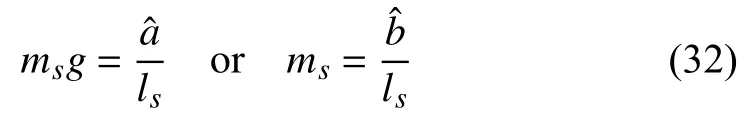
wheregis the gravity and.

For the first spherical joint of the first deformable link,we collect 8 pairs of experimental data,j=1,2,...,8,which are shown in Table II.The experimental data and the data-fitted curve are shown in Fig.7.The residuals of the data-fitted curve are shown in Fig.8.Numerical value of parameter=0.1615 is obtained and its 99% confidence bounds is shown in Fig.7.The sum of squares due to errors(SSEs),R-square,and root mean squared errors (RMSEs)of the data-fitted curve are 0.1112,0.9937,0.1261,respectively.The SSEs,R-square,and RMSEs confirm the correctness of our model.Then we can obtain the estimation of

whereg=9.8 N/kg.

By following the same way,we can estimate,i=1,2,...,8for each spherical joint in the first deformable link.

For the second deformable link,we collect 10 pairs of experimental data,j=1,2,...,10,which are shown in Table III.The experimental data and the data-fitted curve are shown in Fig.9.The residuals of the data-fitted curve are shown in Fig.10.Numerical value of parameter=0.2627 is obtained and its 99% confidence bounds is shown in Fig.9.The SSEs,R-square,and RMSEs of the data-fitted curve are 0.1432,0.9963,0.1261,respectively.The SSEs,R-square,and RMSEs confirm the correctness of our model.Then we can obtain the estimation of,j=1,2,...,8 FOR PARAMETER ESTIMATION OF SpHERICAL JOINTS IN LINk1

TABLE II THE 8 PAIRS OF EXpERIMENTAL DATA

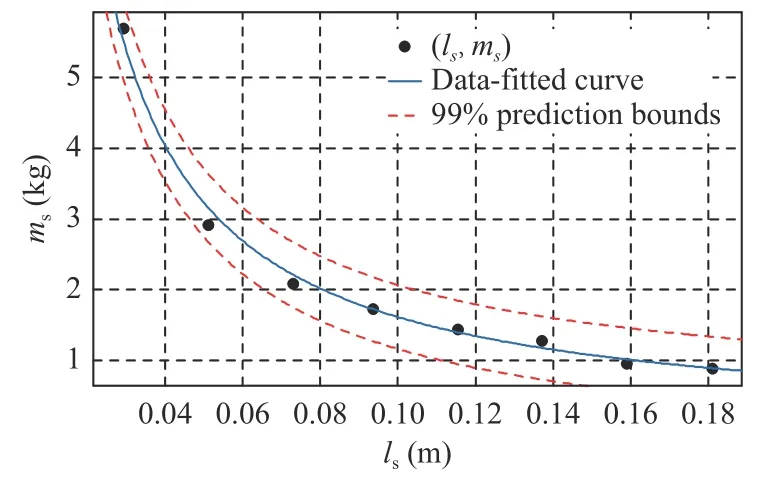
Fig.7.Data-fitted curve for spherical joints in Link1.

Fig.8.The residuals of the data-fitted curve for spherical joints in Link1.

In the same way,we can estimate,i=1,2,...,10 for each spherical joint in the second deformable link.

B.Maximum Payload Mass Prediction

The model prediction of the maximum payload mass is obtained bymmax=Nmax/(l′g),wherel′=l2+l3is the horizontal distance of the acting point on the tip component.To validate our model,we set the two deformable links in various configurations and measure their maximum payload masses in each configuration.The payload is applied to the last component of the deformable link by a fishing line.To improve the accuracy of kinematic measurement by the camera,the deformable links are constrained in a horizontal plane.

The first deformable link is set to 21 different configurations.The second deformable link is set to 25 different configurations.These configurations represent a uniform sampling in the configuration space of the deformable link.

TABLE III THE 10 PAIRS OF EXpERIMENTAL DATA

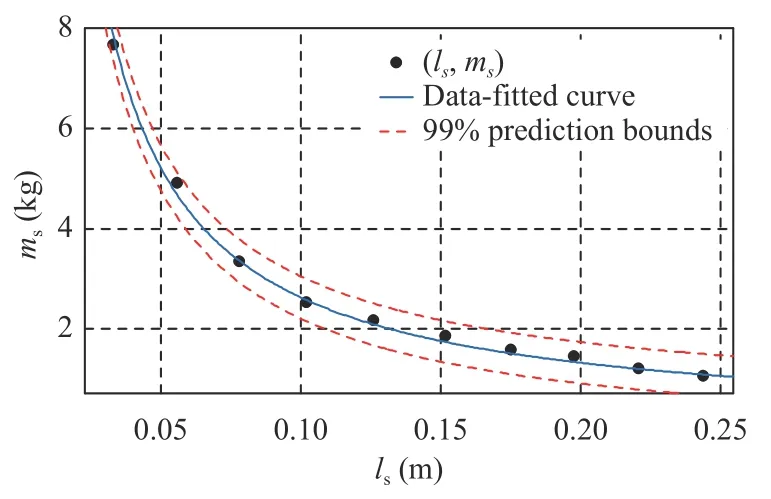
Fig.9.Data-fitted curve for spherical joints in Link2.

Fig.10.The residuals of the data-fitted curve for spherical joints in Link2.

For the first deformable link,the maximum payload masses by the measurement and the model prediction are shown in Fig.11(a).The error statistics are shown in Table IV.As we can see,85.7% of the absolute error values are below 0.15 kg.The mean and standard deviation of percentage errors are 9.53% and 6.73%,respectively.

For the second deformable link,the maximum payload masses by the measurement and the model prediction are shown in Fig.11(b).As shown in Table IV,76.0% of absolute error values are below 0.2 kg.The mean and standard deviation of percentage errors are 12.5% and 10.5%,respectively.The top 5 maximum absolute error values are 0.53 kg,0.51 kg,0.44 kg,0.41 kg,0.34 kg,which are outliers (the sixth highest error is less than 0.25 kg).These outliers can be attributed to two aspects.The first one is that the socket-ball surface is not a perfect sphere,the static friction coefficient changes with temperature,humidity in environment,and so on.The other one is that the accuracy of weightometer is limited.Some errors come from measurements.

Fig.11.The comparison of the maximum payload masses between the measured payload and the model prediction.(a)Comparison for Link1.(b)Comparison for Link2.

TABLE IV THE PERCENTAGE ERROR STATISTICS FOR TwO DEFORMABLE LINkS

The percentage error statistics for the data of the both deformable links are shown in the fourth column of Table IV.The histogram of the total 46 percentage errors is shown in Fig.12.As we can see,80.4% of percentage errors are below 15%.The experiment results demonstrate that our model can achieve a reasonably accurate prediction for the maximum payload mass of a deformable link.Thus our model is validated by the experiment results.

C.Load Bearing Capacity Comparison

In the previous experiments,we choose the maximum load moment on the tip component as the index for load bearing capacity.However,to obtain comparison between manipulators with different scales,we need to calculate the load moment relative to the base frame.We calculate the average values of maximum load moments relative to the base frame in various configurations.As shown in Table V,the average values for the two deformable links are 1.77 N×m and 2.79 N×m,respectively.To our knowledge,only the honeycomb pneumatic network (HPN)structure shown in [18]has considered both flexibility and the load bearing capacity.The HPN structure can bear a load of 2.8 N at a 63 cm distance,namely,the load moment relative to the base frame is 1.76 N×m.The load bearing capacity of our first deformable link with a smaller spherical joint is almost equal to HPN.But the load bearing capacity of our second deformable link with a bigger spherical joint is higher than HPN.This indicates that our deformable link can bear a heavier payload by choosing a proper preload force and radius while loosing little flexibility.Besides,our manipulator can have a smaller size than HPN.

Fig.12.The histogram of the total 46 percentage errors.

TABLE V THE LOAD BEARING CApACITY COMpARISON

VI.CONCLUSION

In this paper,we presented a static force-based model of spherical joints with preload forces and analyzed the static force propagation in the deformable link.This yielded an important result that the load bearing capacity of a spherical joint only depends on its radius,preload force and static friction coefficient.We further developed a parameter estimation method to estimateas a whole.The experiment results validated our model.As we can see,80.4%of percentage errors on the maximum payload mass prediction were below 15%.The comparison with HPN indicated that our manipulator can achieve a higher load bearing capacity with a smaller size.

In the future,the dynamic model of the deformable link will be investigated.The control method to bend the deformable link automatically according to the requirements of different tasks will be developed.