集合复合型结构与集合类属性质的双重分析效能验证——以威伯恩《六首音乐小品》第二乐章为例

唐荣

美国著名音乐理论家阿伦·福特在先后完成于1964年的《音乐集合复合型理论》、1973年的《无调性音乐结构》与1988年的《音级集合类属与现代和声种类的来源》等论文与专著中运用数学集合论的原理，系统而全面地阐释了音级集合理论，对无调性音乐作品音高结构及其关系的分析提供了一种具有普遍意义的理论模式(1)Allen Forte, “A Theory of set Complexes for Music”, Journal of Music Theory，8(1964)，pp.136-183；Allen Forte, The Structure of Atonal Music, New Haven and London:Yale University Press,1973；Allen Forte, “Pitch-Class Set Genera and the Origin of Modern Harmonic Species”. Journal of Music Theory，32(1988)，pp.187-270。国内相关的译著及译介、研究文献可参见：阿伦·福特著、罗忠镕译，《无调性音乐的结构》，上海：上海音乐出版社2009年；王中余：《集合复合型理论的实质、应用与效能》，《音乐艺术》2009年第2期；王中余：《集合类属理论的要点、应用与效能》，《音乐研究》2008年第6期。。事实证明音级集合理论无论对于无调性音乐作品，还是对于调性音乐作品的分析都是行之有效的。

音级集合理论中的集合复合型理论对于无调性音乐作品深层结构的揭示具有重要的意义，“为音级集合的各种关系提供了一种详尽的模式，并为任何无调性音乐作品的分析与阐述建立了一种结构框架”(2)阿伦·福特著、罗忠镕译：《无调性音乐的结构》，上海：上海音乐出版社2009年，第111页。。而集合类属理论则是在集合复合型及其结构框架的基础上，对其基本结构的性质进行进一步的界定、对集合的和声种类的归属及和声风格特性进行归纳与概括。换言之，两种方法都是立足于对无调性音乐作品深层结构的揭示，相对而言，集合类属理论则是在集合复合型理论基础上的发展、延续，但类属更加精确、有效(3)集合复合型理论与集合类属理论的相关概念、释义及计算方法可参见：Allen Forte，“A Theory of set Complexes for Music”, Journal of Music Theory，8(1964)，pp.136-183；Allen Forte：“Pitch-Class Set Genera and the Origin of Modern Harmonic Species”.Journal of Music Theory，32(1988)，pp.187-270.及注中的相关论著。。

基于此，本文提出几个需要进一步思考与关注的问题：在自由无调性音乐作品中，作品音高参数的深层结构关系如何分析？集合复合型是如何联系各个段落并揭示作品的背景结构？再进一步，能否将集合的和声种类进行归属，进而阐释整体的和声风格特性及结构特征？“集合复合型结构”与“集合类属理论”这两种分析结果的准确性、客观性及分析效能如何？文章围绕着上述问题，以威伯恩《六首音乐小品》第二乐章为例，首先对作品中集合复合型结构的揭示，在此基础上，运用集合类属理论的方法为集合分析的结果提供多重分析效能的验证，并探索回答上述问题。

为弦乐四重奏而作的《六首音乐小品》(Op.9)，是威伯恩创作于1913年的一部自由无调性的音乐作品，也是其第一创作阶段(1899—1914)“微型结构”形式的经典之作。作品六个乐章的长度依次为十、八、九、八、十三与九小节，由于各乐章都太过于短小，以至于“感觉不到有任何曲式存在”(4)武田明伦、诸井诚：《新维也纳乐派》(林胜义译)，台北：美乐出版社2002年，第145页。。其中，第二乐章的长度仅有八个小节，更是体现了“格言主义”的创作特征。有证据表明威伯恩之所以追求这种“微型化”的结构、篇幅及细致多样的音色变化，一方面有利于开展某种技术性的实验；另一方面“与他患有神经衰弱症有关”(5)同上，第13页。。

威伯恩在该作品中的某些处理远在老师勋伯格、同门贝尔格之先，并对“十二音”体系的形成产生了深远的影响。如威伯恩为了追求音色的“敏感度”，使音色产生细致而多样的变化，在六个乐章中全部乐器基本都装上弱音器并以极轻的力度进行演奏。同时，作品音高的“半音化”程度很高，半音的堆积及其转位、复音程、半音之间返身跳进和纵向叠置不但使音与音之间的关系变得模糊，而且在音色的配合下也使音响具有细致而微妙的变化。这种音色与音高的处理方式，一起对传统的调性观念产生了强烈的冲击。

一、集合复合型及相互关系

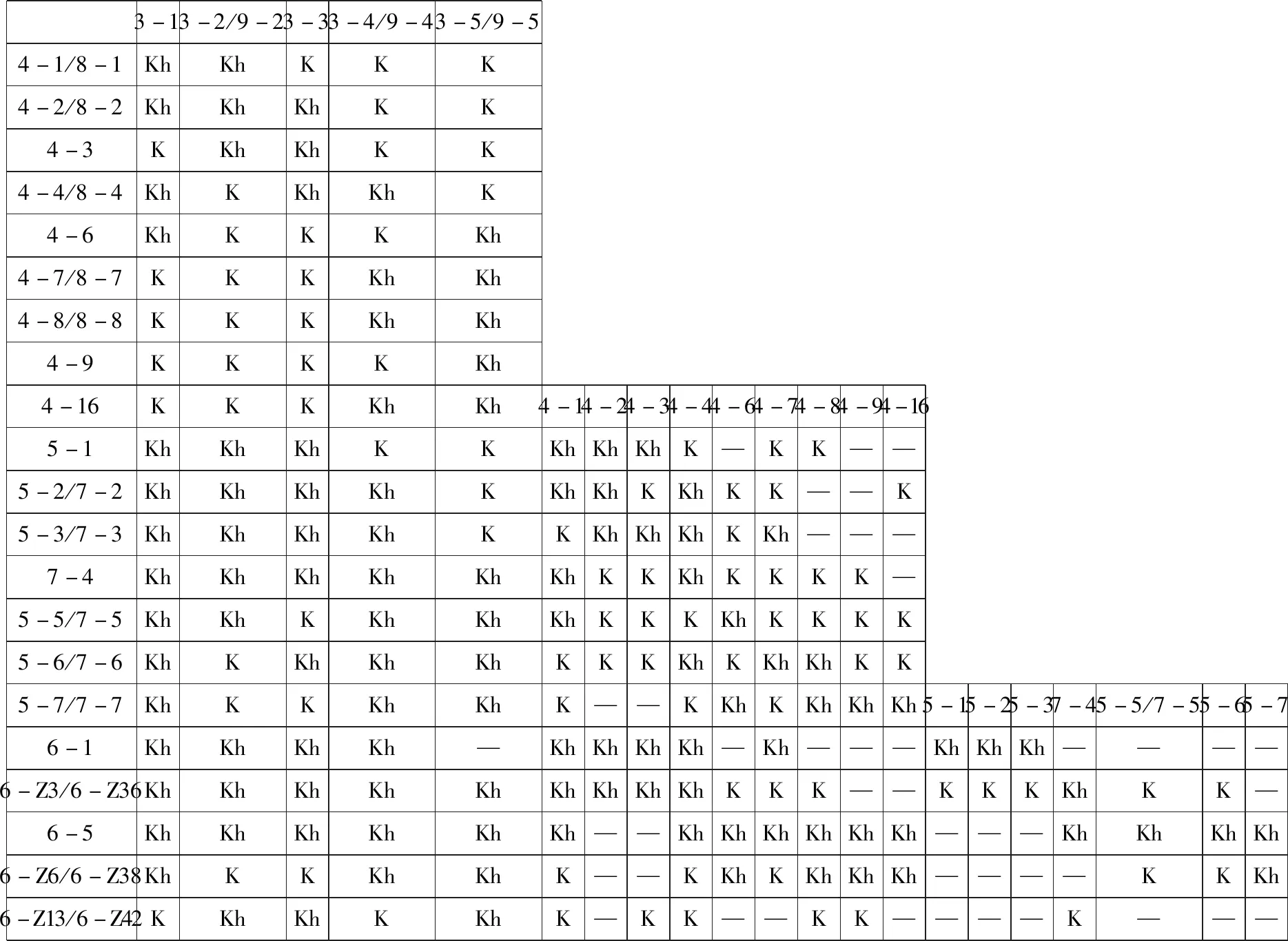
表1. 整体的集合复合型关系：主要联系集合为6-Z3(6)图表分析的目的在于观察一部作品或片段不同基数集合之间的集合复合型关系及不同集合之间的关联程度，同时确定集合复合型结构的联系集合。关于联系集合的确定福特制定了三个规则：第一，优先考虑六音集合，因为它具有封闭性。第二，Kh与K*关系最大数量的集合暂时定为首要的联系结合。第三，次要联系集合如果与主要联系集合的基数相同，那它必须要与所有和主要联系集合没有集合复合型关系的集合具有集合复合型关系。同时，还需要再找一个附加的次要联系集合，这个集合必须要和主要联系集合与次要联系集合产生集合复合型关系。参见：阿伦·福特著、罗忠镕译，《无调性音乐的结构》，上海：上海音乐出版社2009年，第134—135页。，第一辅助联系集合为6-5，第二辅助联系集合为5-6。

表1表明了全曲的集合复合型结构是连通的，主要联系集合为6-Z3，第一辅助联系集合为6-5，第二辅助联系集合为5-6。另外集合4-1、4-4与所有集合都有复合型关系，并且大多数都具有Kh关系(7)集合复合型是指根据包含关系与某个集合(特指联系集合)相联系的一组集合，一般有两种类型：第一种覆盖面较大，用K表示；第二种是子集合复合型，规模较小并有一定的限制，用Kh表示。集合复合型是衡量某个特定的集合与其具有包含关系的所有集合之间的相似程度，再根据包含关系“反向互补”的性质，观察某个特定的集合与其子集(或母集)之间的关系，进而扩展到该集合的补集与其子集(或母集)之间的关系。由于集合复合型K的成员相当广泛，需要将集合复合型观念加以提炼，于是福特提出了第二种子集合复合型Kh的概念，子集合复合型Kh是对集合复合型K的筛选，它的成员与联系集合之间具有最高程度的相似性，由于包含关系的集合复合型中结合了交互性补关系(reciprocal complement relation)，导致了集合复合型结构的对称性。具体参见: 阿伦·福特著、罗忠镕译，《无调性音乐的结构》，上海：上海音乐出版社2009年，第111—120页；王中余：《集合复合型理论的实质、应用于效能》，《音乐艺术》2009年第2期，第73—74页。。

二、集合关系及其结构功能

《六首音乐小品》(Op.9,No.2)虽仅有8个小节，但通过对乐曲形态与集合复合型关系的分析，特别是通过音级集合的运动，发现该曲可以划分成为四个片段，并具有一定的“三部性”或“起承转合”的结构意味。为了论述方便分别用“片段一、二、三、四”表示。

片段一(第1—2小节)，核心集合3-4〔4,8,9〕出现在作品的一开始，并与随后出现的复合截段9-4〔9,10,11,0,1,2,5,6,7〕形成了互补关系。值得注意的是这里的集合3-4与9-4之间没有音高的重叠，两者刚好构成了完整的“十二个音级”，这说明威伯恩在作品的一开始就力求“消除”各音级之间的“等级”差异，做“均匀”的消耗完整“十二个音级”的实验。另外，在片段一的低声部隐伏了全曲最重要的联系集合6-Z3〔11,0,1,2,4,5〕，它“镶嵌”在中提琴与大提琴声部之间(见谱例1b)，它是核心集合3-4的母集，这两个集合在随后的段落中还将在不同的音高位置出现，使乐曲在乐思上显得更加统一与集中。

片段二(第3—4小节)，集合5-2〔5,6,7,8,10〕与集合4-7〔11,0,3,4〕构成集合9-2〔3,4,5,6,7,8,10,11,0〕，集合9-2与第四小节的集合3-1〔0,1,2〕构成了片段二的所有音高内容。第三小节中提琴、大提琴声部演奏的集合3-4〔11,3,4〕既是片段一中核心集合3-4〔4,8,9〕的移位(t=7)，又是集合6-1〔11,0,1,2,3,4〕与4-7〔11,0,3,4〕的交集。同时集合4-7既是集合8-7〔11,0,1,2,3,4,7,8〕的子集，又与集合8-7形成了互补关系。

片段三(第4—5小节)是全曲的高潮部分。该片段不仅音区跨度大、截段数量多、发音点密集，而且与前后段落在补关系上联系紧密。第四小节第二小提琴声部的集合3-4〔6,7,11〕是片段一核心集合的反演移位(it=3)，它与复合截段集合5-1〔11,0,1,2,3〕构成集合7-6〔11,0,1,2,3,4,6,7〕。中提琴声部的横向截段集合4-7〔4,5,8,9〕是片段二同一集合的移位(t=5)，它与大提琴声部的横向截段集合4-6〔3,4,5,10〕构成了复合截段集合6-Z6〔3,4,5,8,9,10〕，其不变子集是〔4,5〕，集合6-Z6与片段一的集合6-Z38互为补关系。复合截段集合6-Z6〔3,4,5,8,9,10〕与集合7-6构成了片段三的所有音高内容。其中，集合6-Z38与集合6-Z13、集合6-Z36与片段一、五中的主要联系集合6-Z3、辅助联系集合6-5与片段一、五中的集合6-5都形成了互补关系。如此，片段三在与前后段落之间形成巨大反差的“表面”，在音高结构的深层次上形成了既相互对比，又密切联系的关系。

片段四(第6—8小节)作为全曲最后一个部分，“再现”了全曲重要的集合。主要联系集合是6-Z3，辅助联系集合6-5与3-1构成了该片段的所有音高内容。集合6-Z3〔9,10,11,0,2,3〕是片段一同一集合的移位(t=2)，集合6-5〔11,0,1,2,7,8〕是片段一集合6-5〔10,11,0,1,6,7〕的移位(it=1)，集合6-1也是片段二同一集合的移位(it=1)。

谱例1a.威伯恩《六首音乐小品》(Op.9，No.2)的集合分析

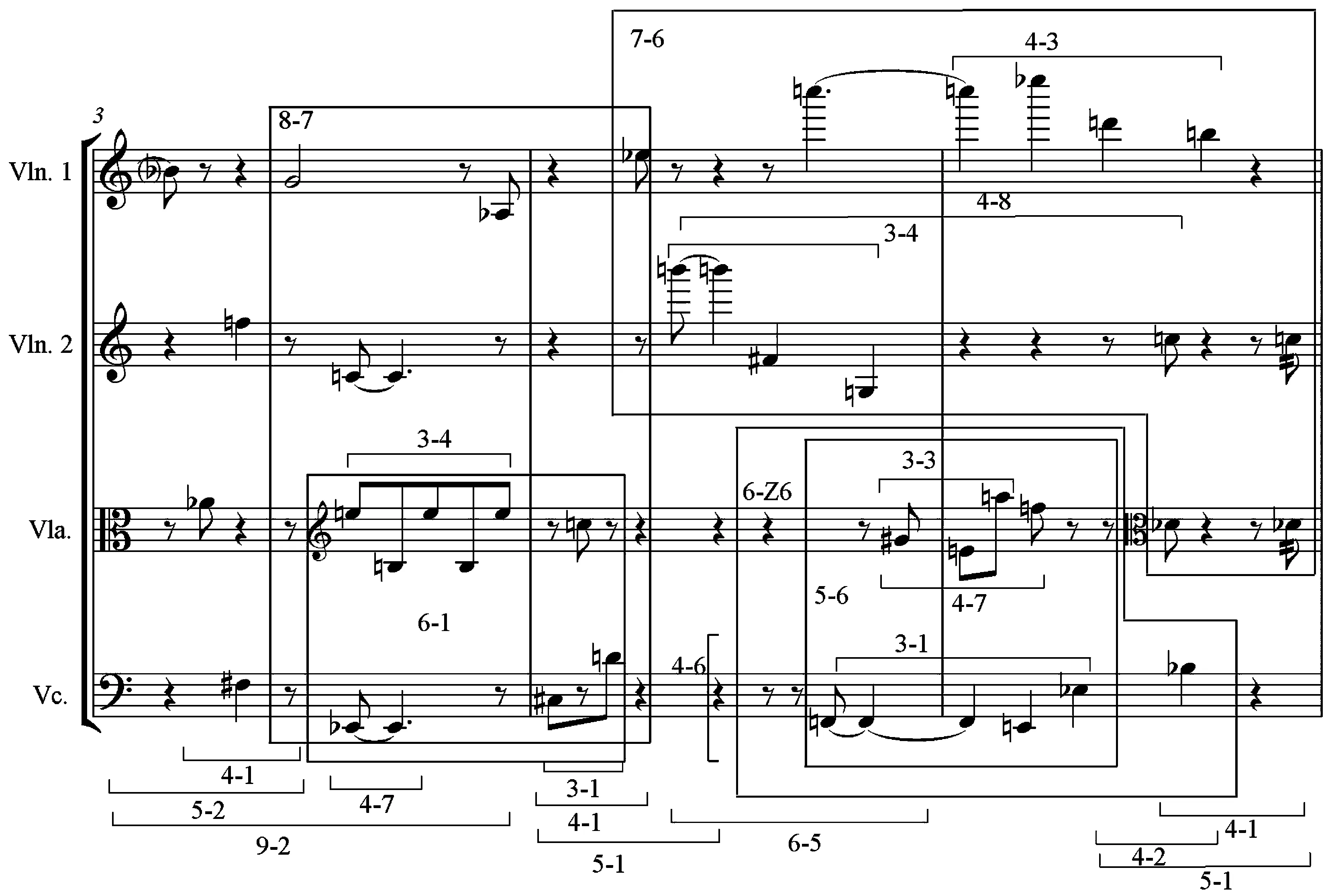
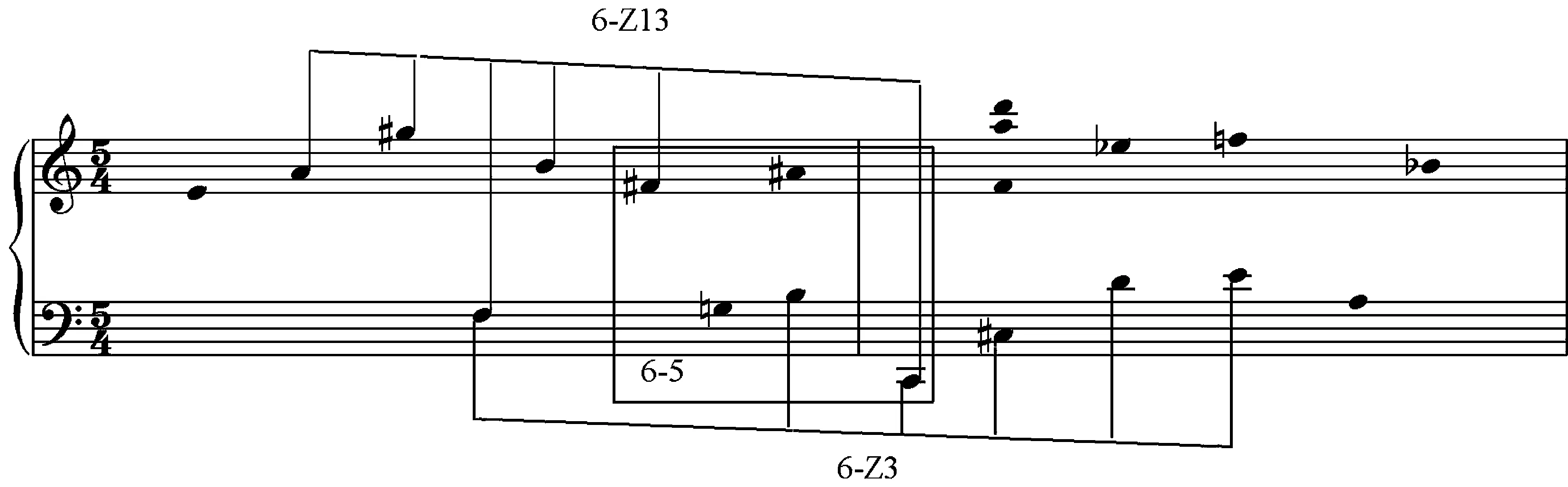
谱例1b.

三、曲式结构单位间的集合联系

补关系在无调性音乐中是一个重要的结构性特征，呈互补关系的两个集合所构成的十二音全集，对后来“十二音体系”的出现在一定程度上具有潜在的影响。对全曲进行截段划分，共有26个集合，其中有16个是补关系集合。

在片段一中，核心集合3-4与随后出现的复合截段集合9-4形成互补关系，两个集合之间没有音高的重叠，在音乐的开始就将十二个音级全部出齐。纵向截段集合4-7与片段二的集合8-7互补，片段三、四中的集合4-7分别也是它的移位(t=10)、(t=2)。片段二具有承接发展与连接过渡的功能。它的集合9-2、集合4-1与片段一的集合3-2、集合8-1为互补关系。其中，片段三中的集合4-1是片段二同一集合的移位(t=5)。

相对其它片段而言，片段三与片段一之间的互补集合最多，两个片段之间的六音集合有四对为互补关系，它们分别是：6-Z38/6-Z6、6-Z13/6-Z42、6-5/6-5与6-Z3/6-Z36。特别是片段一中的主要联系集合6-Z3、第一辅助联系集合6-5、第二辅助联系集合5-6，都与片段三中的相应集合形成互补关系。正是因为互补关系，使得位于呈示与展开、对比功能位置上的两个段落，在表层形成鲜明对比的同时，又在深层音高结构上形成紧密联系。

片段四具有明显的综合再现性质，它的集合9-5是片段一3-5的补集；半音化的集合6-1则是片段二同一集合的移位(t=11)。最为重要一点就是再现了片段一中的主要联系集合6-Z3、第一辅助联系集合6-5、第二辅助联系集合5-6(片段四中的这些集合也与片段三中的相应集合形成互补关系)，另一重要的联系集合4-4也与片段一中的集合8-4构成互补关系。

根据谱例1的分析与表1的统计，作品中的九个四音集合分布在四个片段之中。表2显示出作品中的四音集合之间具有密切的传递关系，特别是集合4-2、4-4、4-6、4-8、4-16都与三个四音集合具有传递关系，并且大多数具有R1+Rp或R2+Rp的关系(8)表2与表3中的Rp为音程级极大相似性；R0为音程级极小相似性；R1为音程级极大相似性，有互换的特点；R2为音程级极大相似性，无互换的特点。具体参见: 阿伦·福特著、罗忠镕译，《无调性音乐的结构》，上海：上海音乐出版社2009年，第60页。。在五音集合中，除了集合5-7未与其它同基数集合产生联系以外，其它五音集合都与二个及以上的五音集合具有传递关系(见表3)。

表2. 四音集合之间的相似性关系

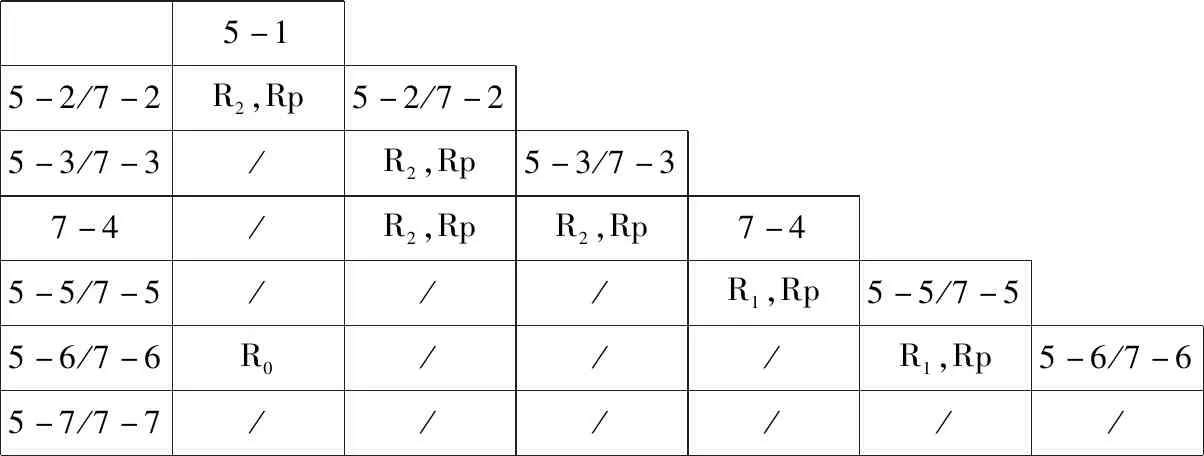
表3. 五音集合之间的相似性关系

四、半音音程模式及“十二音体系”的“先现”

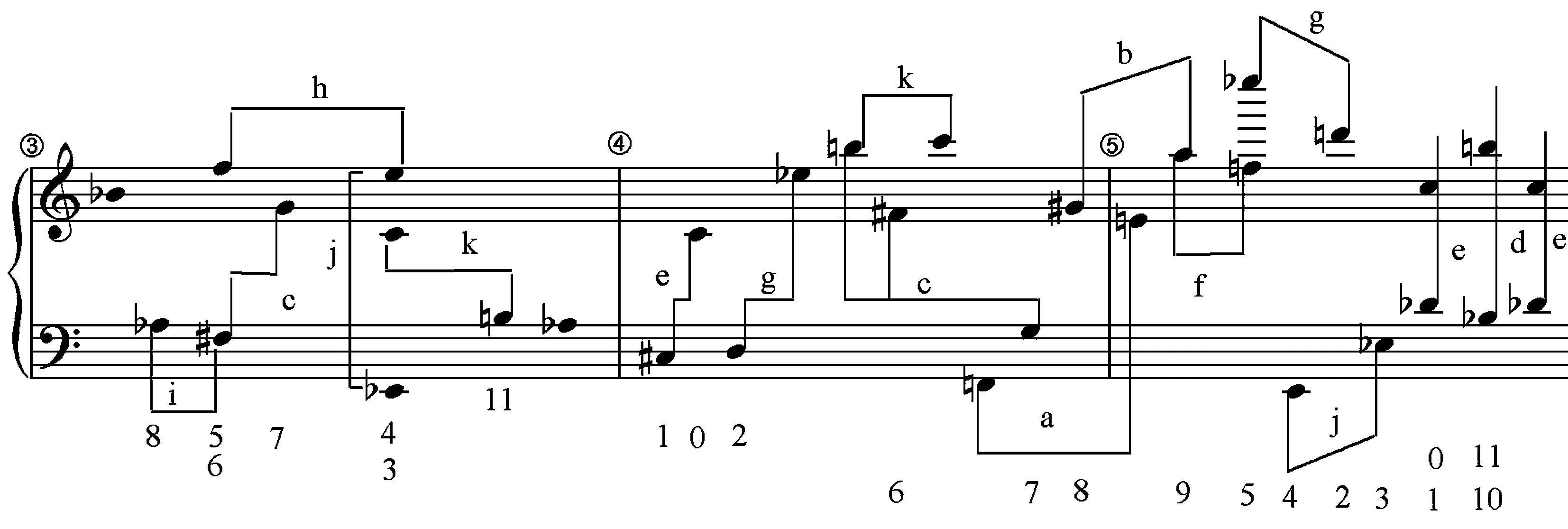
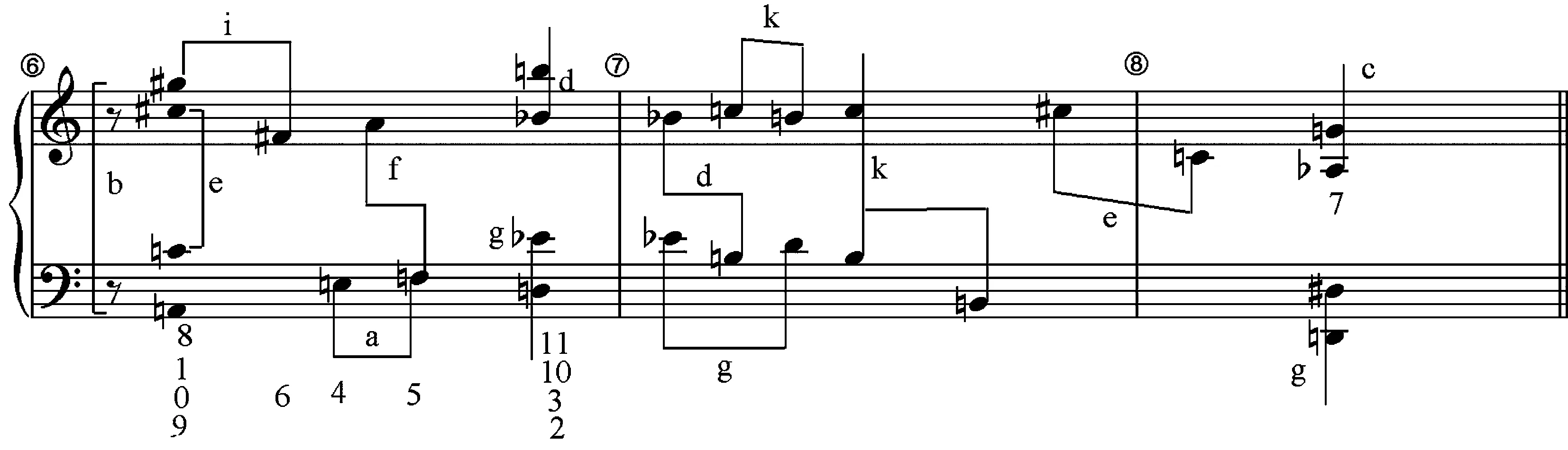
全曲在音高结构层面可分为11种固定音级的半音音程模式(在谱例2中用a-k标记)，除了模式f、i分别为大三度、大二度以外，其它模式均为小二度或其转位。如谱例2所示，全曲所有的音高内容均由这11种固定音级的半音音程模式及其重复所构成，某些重复的音程模式，虽然有音区的变化，但却保持了音程模式的固定音级不变。除此之外，作品中的四个片段，每个片段中均出现一个完整的“十二个音级”，有些是非常明显的，诸如片段一核心集合3-4及其补集9-4之间没有音高的重叠，有些则是将十二个完整的音级镶嵌在音乐片段之中。无论威伯恩当时的这种处理是否有意识，但是通过对乐谱文本的解读，可以窥探出威伯恩已经开始向“十二音体系”的历程中迈出了重要的一步。

谱例2(9)谱例2中的第1、2、4、5、6小节的谱面分析部分参考了Allen Forte, The Atonal Music of Anton Webern,Yale University Press New Haven &London.(1998).p.179..

五、类属关系的分析阐释(10)福特将208个无序音级集合归属到12个类属之中，不同类属的结构与性质呈现出明显的差异，12个类属的性质依次为无调性、全音、减、增、半音、准半音、半音—自然音、无调性、无调性—调性、自然音、自然音—调性等。后文中有关类属关系的算法公式均引自王中余：《集合类属理论的要点、应用与效能》，《音乐研究》2008年第6期。有关类属理论的具体阐释与算法可参见该文，故本文不再赘述。

通过上述对威伯恩《六首音乐小品》(Op.9,No.2)进行截段取样并对其集合复合型结构的分析与阐释，在此基础上确定了26个(对)集合，这些集合分别是相同或不同类属的成员。在表4中显示了这些集合与各类属的归属情况、类属关系的阐释规则(下表的左列与最上行)及各类属成员的出现次数(下表的最后一行)。

根据表4中的统计，将这些集合类属的整体规模、各类属成员的出现次数等方面进行综合考量，通过运用位置商的计算公式(位置商Ga=〔(X/Y)/Z〕×10)便可得出各类属的位置商(11)在这个公式中，变量X是类属a在矩阵(见表4)中的代表数；Y是矩阵中所有集合的数目；Z是类属a的整体规模，乘以10是为了使差数商的小数点向左移动一位。。根据位置商的计算结果，结合根据阿伦·福特提出的五个集合类属的阐释规则——“1.最大位置商规则；2.相交规则；3.完成规则；4.独立延伸规则；5.消减规则”，进而便可确认26个集合的类属归属。如将主要联系集合6-Z3与第一辅助联系集合6-5归属到类属5，因为根据规则1类属5的位置商最大。同理，还有诸如集合3-1、集合4-1、集合5-1与集合6-1等本身都具有高度半音化的特征，再根据位置商的计算，也将这些集合归属到类属5。将第二辅助联系集合5-6及核心集合3-4归属到类属8，是因为位置商最高的类属不能对这两个集合进行解释，而根据规则3类属8的位置商居第二(见表5)。

表4.

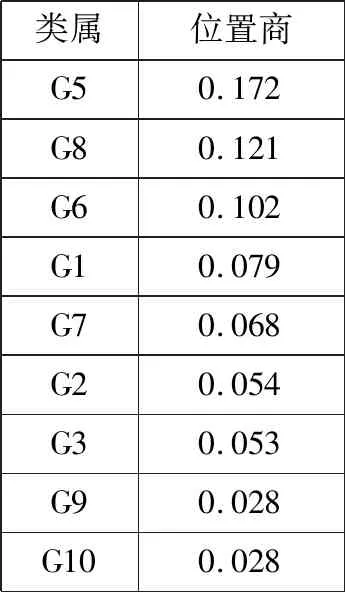
表5.

根据上述计算再进一步进行归纳，可以用4个类属来概括这26个集合的和声种类，从表6可以看出类属5、类属1与类属8是这个乐章的主要的和声种类，它们分别属于“半音”与“无调性”的性质。而唯一一个类属6的集合4-3，它也具有“准半音”的性质。因此，“无调性”是全曲重要的“和声”性质，这也与前述的分析结果相应。

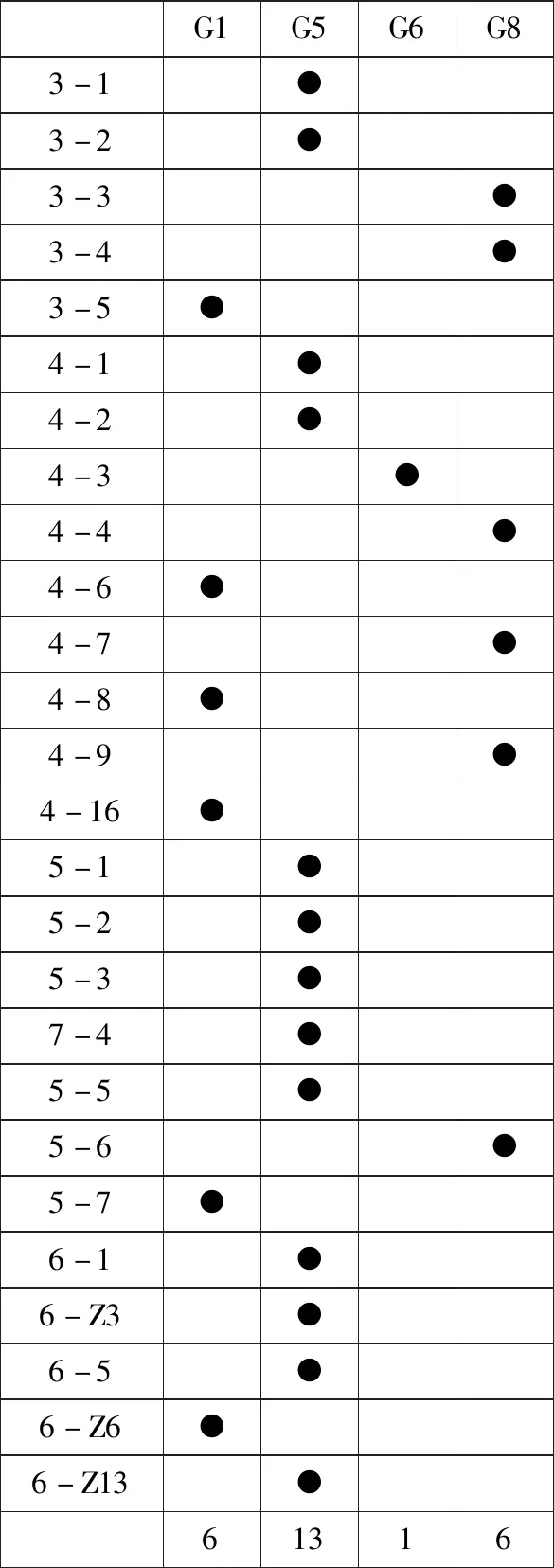
表6.

从“调性”到“无调性”再到“十二音体系”是逐步演进的结果，而音级集合理论对于无调性音乐作品结构的揭示具有重要意义。文章通过上述对威伯恩《六首音乐小品》(Op.9，No.2)从“集合复合型及相互关系”“集合关系及其结构功能”“曲式结构单位间的集合联系”“半音音程模式及十二音体系的先现”与“类属关系的分析阐释”等五个方面的分析论述，初步回答了摘要中提出的几个问题，并得出如下几个结论：

第一，集合复合型对于联系无调性音乐作品的各个段落，揭示无调性音乐作品的深层结构具有重要的意义。本曲中的集合复合型结构是连通的，主要联系集合为6-Z3，第一辅助联系集合为6-5，第二辅助联系集合为5-6。同时，通过对作品音级集合关系的揭示，可知全曲具有“起承转合”的结构意味。

第二，补关系是全曲的重要特征，作品中部分位置连续无重复的出齐十二个音级，都是由于补关系对所构成。它与作品中的“半音音程模式”一起在一定程度上对 “十二音体系”的出现起到了促进的作用。

第三，通过对类属关系的分析阐释与计算、对集合的和声种类归属的界定与和声风格特性的归纳，界定了“半音化”与“无调性”是全曲重要的“和声”风格特性。因此，本文通过集合复合型理论分析无调性音乐作品的基本结构，再运用类属理论的计算对其性质进行进一步的界定，双重分析效能的验证保证了分析结果的准确性与客观性，进而使分析结果更加精确、有效。