经历模型生成 助力思维提升*——“一线三等角相似”的教学设计及思考

许 彬 耿恒考 (江苏省苏州中学园区校 215021)

1 缘起

我国著名数学家华罗庚曾说：“任何问题，一旦建立起了数学模型，就会立即显现出解决问题的清晰途径和通向胜利的一线曙光！”可见各种数学模型对解题起着举足轻重的作用.许多教师在日常教学中热衷于给学生归纳各种数学模型，并且只注重教授结论和应用，这样做主要是为了方便学生在解题时能够熟练地套用模型，实现快速解题的目标．但他们却忽视了模型生成的过程，使提升学生数学思维的效果大打折扣，更直接影响到学生数学能力与素养的有效发展和提高．前不久，在苏州市教育局直属学校举行的一次初三教学研讨活动中，笔者有幸开设了一节示范课，主题是苏科版九年级下册第六章“相似三角形”中的“一线三等角相似”．笔者基于学情设计的问题层层递进，学生在问题的引导下经历模型的完整生成，并且在知识生长处有效训练，既发展了学生的数学能力，又高质量地提升了学生的数学思维，因此得到与会师生的一致好评．

2 教学设计与分析

九年级学生在学习本节课内容之前已经在八年级上册“全等三角形”中接触过用模型解决三角形全等的相关问题.该模型根据角的位置关系被称为“一线三等角”，从形状的角度看被称为“K型图”，解题时通常又被细分为同侧、异侧两类，一线三直角、三锐角、三钝角三种.

因此，本节课的教学重点是通过问题引领学生形成一线三等角相似的模型体系，并在灵活运用模型解决问题的过程中有效提升数学思维；难点是通过教学活动促进知识生长，增强数学能力，提升数学素养．

2.1 类比抽象，提取模型

(1)问题1：将含45°角的直角三角板的直角顶点放在坐标系的原点(图1)，已知点A(2，1),求点B的坐标．

图1 图2

变式：将含30°角的直角三角板的直角顶点放在同样位置(图2)，若点A(2，1),求点B的坐标．

教学分析首先，问题1以学生常见的等腰直角三角板为背景，如图3，分别从点A，B向x轴作垂线，垂足分别是点C，D，在等腰直角△AOB中AO=OB，由一线三直角全等模型可得△AOC≌△OBD，则由点A坐标知AC=OD=1，OC=BD=2，因为点B在第二象限，所以点B的坐标为(-1，2).此题起点低，比较容易解答，目的是为了让学生回顾全等模型．其次，由变式题类比问题1的解法，如图4，分别由点A，B向x轴作垂线，

图3 图4

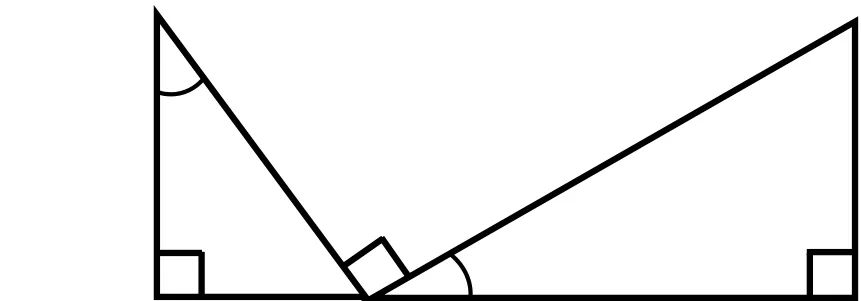
图5

(2)变化角度，模型延伸

问题2：如果将图5中的直角变为任意角(锐角或钝角，如图6、图7)，结论还能成立吗？请同学们交流并给出证明．

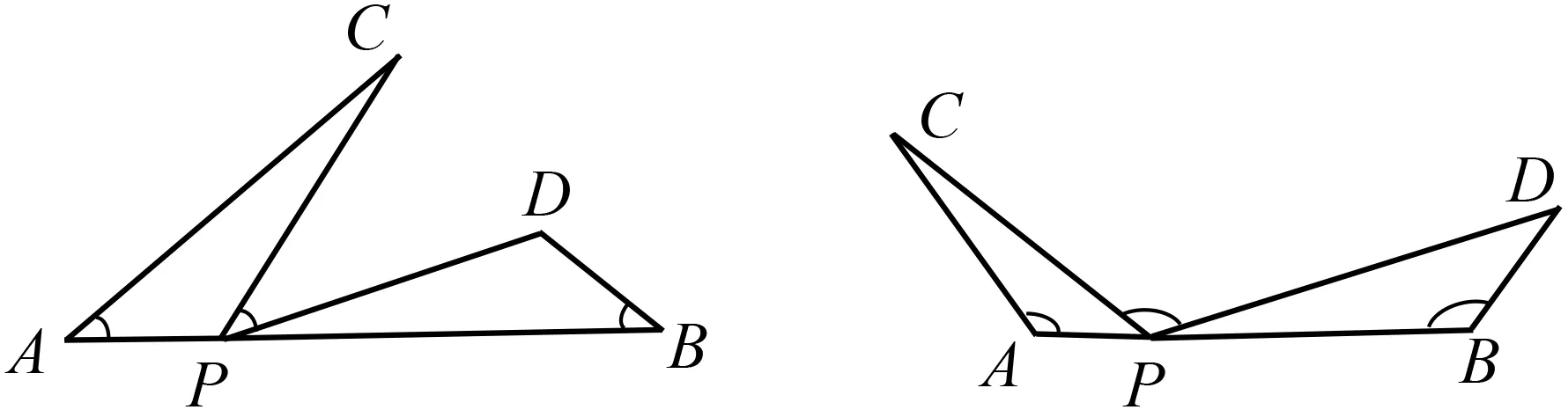
图6 图7

教学分析问题2用角度变化引导学生完善同侧一线三等角模型(图6、图7)，让学生寻求变化中的不变，即角度大小变化了，但一条直线上的三个等角没变，所以三角形仍然相似，使学生学会以辩证的视角分析问题，形成辩证思维能力．课堂第一个环节通过平面直角坐标系中的一副直角三角尺构造的问题1和变式题，以一线三等角全等作为引题，用直观类比的方式抽象出相似模型，再由问题2引导学生对一线三等角的同侧模型予以完善，由此，学生通过学习在知识最近发展区内形成新知和能力．

2.2 初步应用，完备模型

(1)问题3：如图8，正方形ABCD的边长为5，点P，Q分别在直线CB，DC上(点P不与点C，B重合)，且∠APQ=90°，当CQ=1时，求出线段BP的长.

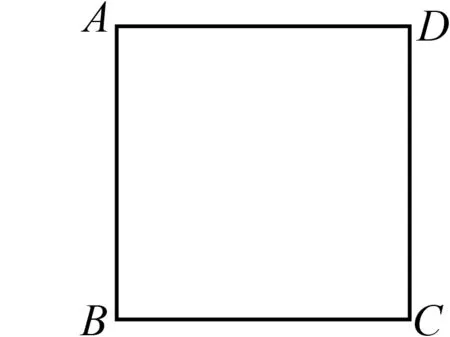
图8

问题分解(用PPT逐条呈现)：

(1)请在直线CD上画出CQ=1的所有可能情况(图9)；

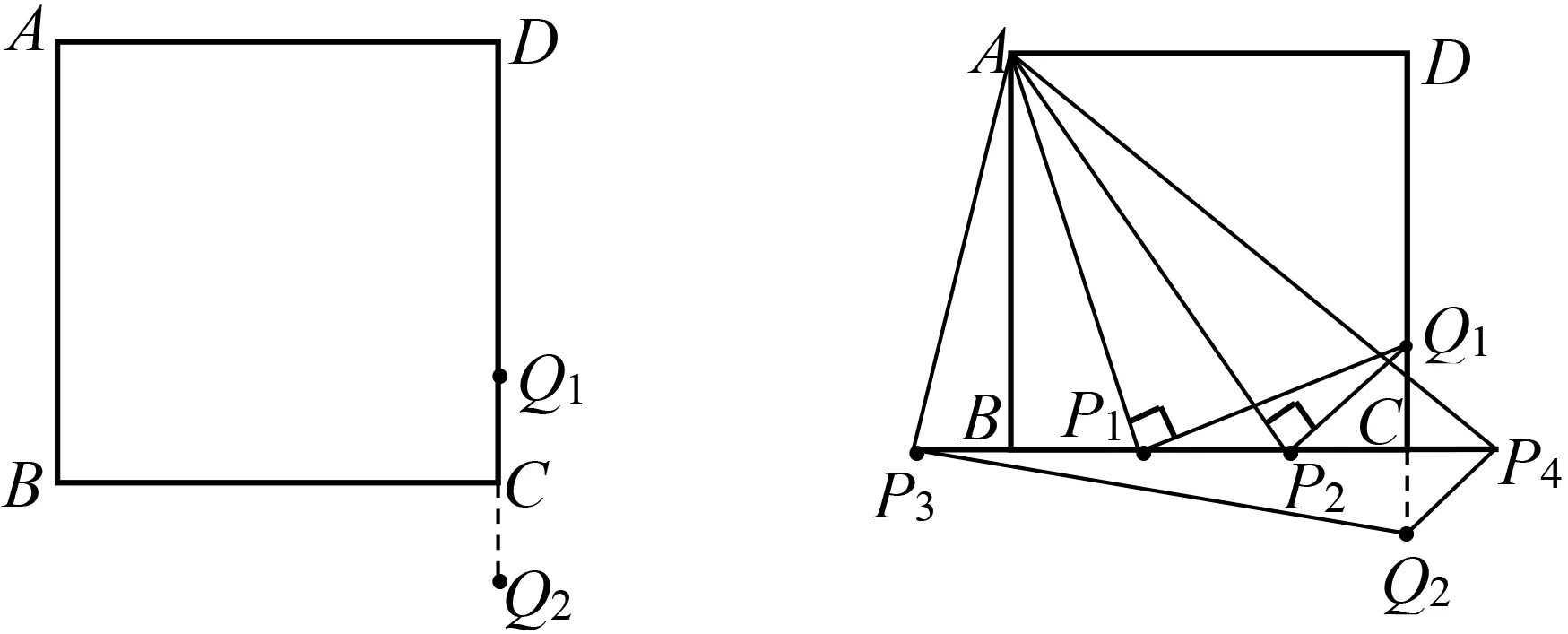
图9 图10

(2)当∠APQ=90°时，请在直线BC上确定点P的所有位置(图10)；

(3)根据所画图形，求出线段BP的长.

教学分析在一线三等角同侧模型形成后，问题3可以实现两个教学目标：一是对已有模型进行巩固和强化；二是为探究异侧模型图埋下伏笔．教学中教师为了降低探究难度，给教学重点预留时间，将问题3“拆解”成三个小题：题(1)是根据条件画出点Q所有位置(图9中的Q1，Q2)，说明点Q不唯一；题(2)根据∠APQ=90°找出所有符合条件的直角顶点P(即图10中的P1～P4)的四个位置；题(3)在图10的直观条件下，利用三角形相似求出线段BP的长度．在解题的最后阶段，教师引导学生根据∠AP3Q2=90°和∠AP4Q2=90°的情况抽象出一线三等角异侧模型(图11)．

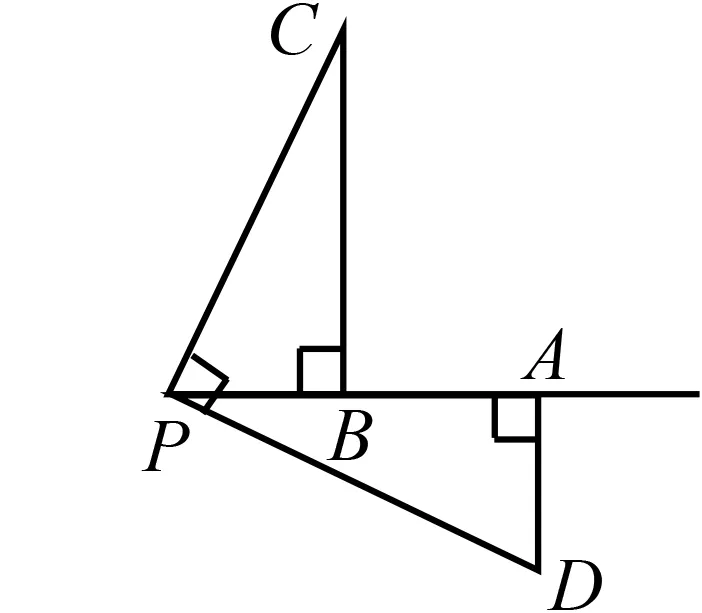
图11

(2)问题4：如果将直角(图11)变为任意角(锐角(图12)或钝角(图13))，结论还成立吗？请写出你的证明过程．

图12 图13

教学分析问题4是借势将刚刚抽象出的模型图11中直角变化成锐角、钝角(图12、图13)，让学生完成证明过程，至此完备了一线三等角相似模型的所有情况，提升学生思维能力的落脚点也得到固化．

2.3 应用模型，提升思维

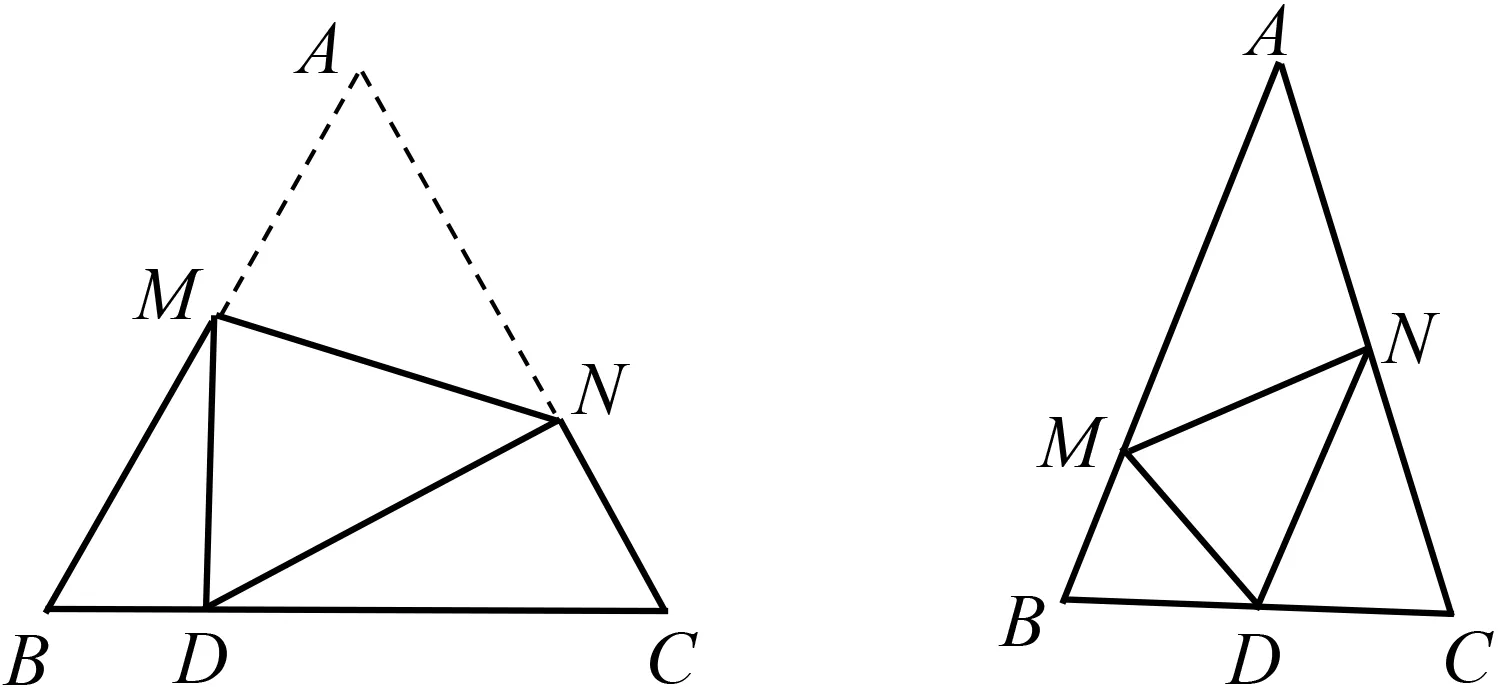
图14 图15

变式：如图15，在等腰△ABC中，AB=AC，D是BC的中点，且∠MDN=∠B．

(1)请找出图中所有的相似三角形；

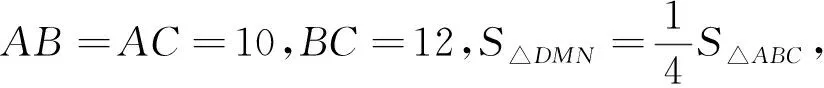
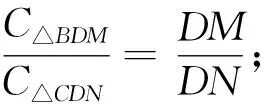
2.4 归纳整合，构建体系

问题6：同学们清楚本节课所有模型图之间的关系吗？请概括它们的关系及异同点．

教学分析问题6是为了引导学生建立完整的一线三等角相似模型体系，在问题效能的驱动下，学生们一起梳理、补充、整合分散着的模型图谱；通过教师激励，学生猜想、试错、辨析等系列教学活动，最终架构起一线三等角证明相似三角形的模型体系(图16)．至此，学生经历了模型的产生、发展、完备、整合，在问题解决中形成模型体系，从数学知识到思维能力都在上升，也是为用模型解决综合性问题蓄力．

图16

2.5 综合应用，思维拔高

问题7：如图17，在平面直角坐标系中，直线l1：y=-2x+4与x轴、y轴分别交于A，B两点，将△AOB沿l1翻折，点O的对称点为P．

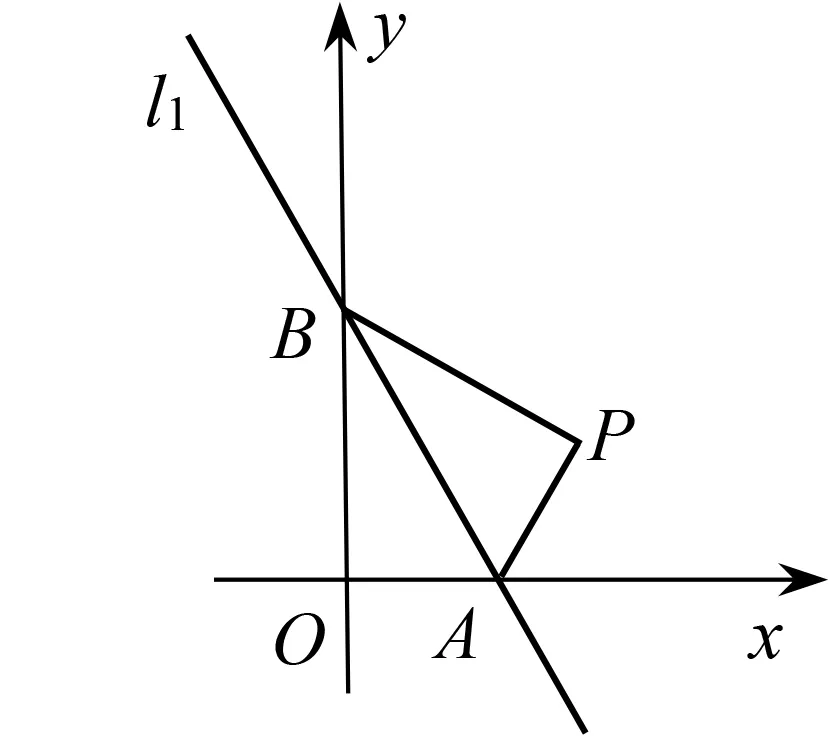
图17

(1)求点P的坐标；

(2)若直线l2过点P，且与直线l1的夹角是45°，求两直线l1，l2的交点坐标．

图18 图19

3 思考

本次教学通过问题引领学生经历模型的抽象-延伸-完备-整合-创建-综合应用，问题从简单到复杂，知识由具体到抽象，教学思路清晰明了，知识层层递进，思维拾阶而上[2]，学生逐步养成用数学模型进行思考的学习习惯．

3.1 用问题引导学生经历模型生成

数学模型就是根据特定的研究目的，采用形式化的数学语言，抽象地、概括地表征所研究对象的主要特征、关系所形成的一种数学结构．史宁中教授在《数学思想概论》中提出这样的观点：“数学发展所依赖的思想在本质上有三个：抽象、推理、模型……”，可见模型对学生学习、研究数学的重要意义．基于此，教学中教师通过设计层层递进的问题引导学生经历建模过程，使学生在探究中积累学习经验，掌握建模方法，而不是直接给学生模型．本课教学伊始，教师通过问题1及变式让学生既回顾全等模型，又用类比的方式抽象出直角相似模型，新知生成自然合理；再通过变直角为锐角、钝角，形成同侧模型，此环节并不是仅仅变角度，还引导学生说出相似依据，模型得到完美延伸；问题3的研究既可以实现运用已知模型解决问题，又能引申出异侧模型，进而使模型得以完备，也让学生明白研究异侧模型的必要性．在学生经历了模型的抽象、延伸、完备之后，学生的学习探究活动并没有戛然而止转入解题训练环节，却是用问题6引导学生将所学全部模型进行整合，构建起本节课学习新知的体系，也是对本节课学习所得的总结，这对训练学生“四基”“四能”有强基固本的作用．

3.2 紧扣知识生长点，助力思维提升

数学是思维的体操，本课不能把学生单纯会用模型解题作为教学活动的终点，教师应注重通过解决螺旋上升的问题提升学生数学逻辑思维的品质．由开始的问题1(放在平面直角坐标系中的一副三角尺)抽象出模型，做为本课知识教学的生长基点；问题3在讨论、探究中能看到模型的影子，还需要新的模型出现才能完整解决问题；问题5在强条件之下应用模型解决问题，学生会直接感受到模型给解题带来的好处；然后变式题将条件弱化，让学生强烈感觉到学习模型的必要性；最后，问题7中的题(1)需要学生思考如何添加辅助线创建相似模型才能解决问题，而题(2)则要学生利用已知条件45°构造出等腰直角三角形，并在此基础上再次添加辅助线构造模型证明全等才可以顺利解决问题．这里所有的数学问题都是知识的延伸点和思维的外显形式[3]，利用问题解决活动有效地提升了学生数学思维的广度和深度．

本课并没有将数学模型教学“模式化”地直接给出，而是引导学生经历模型生成及应用，不仅注重知识的“生长点”还重视知识的“延伸点”[1]，强化学生对知识的整体把握和宏观认识，对提升数学思维和形成数学素养是十分有效的．