立足于数学核心概念的教学基本结构*——以“等比数列”复习课为例

孙冬梅 (上海市进才中学 200135)

随着2017年版(2020年修订)普通高中数学课程标准的颁布，课堂教学价值追求开始由单纯的知识传授向素养整体培育转型，以核心素养为导向、以知识构建为基本特征的课堂教学成为主流．对于数学学科而言，数学概念是数学逻辑中的最基本单元，是核心素养培育的起点，而数学核心概念更是数学概念结构的核心和基础．因此，本文基于数学核心概念开展数学教学研究，以数学核心素养培育为目标，探寻概念教学基本结构；以“等比数列”复习课为例，进行具体教学实践．

1 核心素养视角下数学核心概念教学的目标定位

以核心素养为培养目标的数学核心概念教学，追求的是学生能建构概念、理解概念和发展概念.

(1)概念建构有坡度：即指通过数学核心概念的获得，学生不仅能够知道概念的表述，更能经历形象感知、建立表象、数学抽象等概念建构的过程，在概念建构中感知数学概念产生过程，夯实数学直观想象、数学抽象等数学思维素养．

(2)概念理解有深度：即指通过数学核心概念的多层次理解，学生不仅能够认识知识的表象，更能深刻领会知识的本质及蕴含的数学思想与方法，在形成数学对象过程中运用数学方法和思考方式，在解构概念的过程中推演数学过程，提升数学方法素养．

(3)概念发展有广度：即指在深度理解的基础上，学生能通过对数学核心概念的应用，从多角度对知识进行审视并且合理解释与应用，掌握运用数学知识和方法来解决问题的基本途径和工具，感受数学价值，发展数学工具素养．

2 核心素养视角下数学核心概念教学的基本结构

对应数学核心概念的三层教学目标追求，其教学环节设计应把握“三个阶段十一环节”的基本结构(图1)．

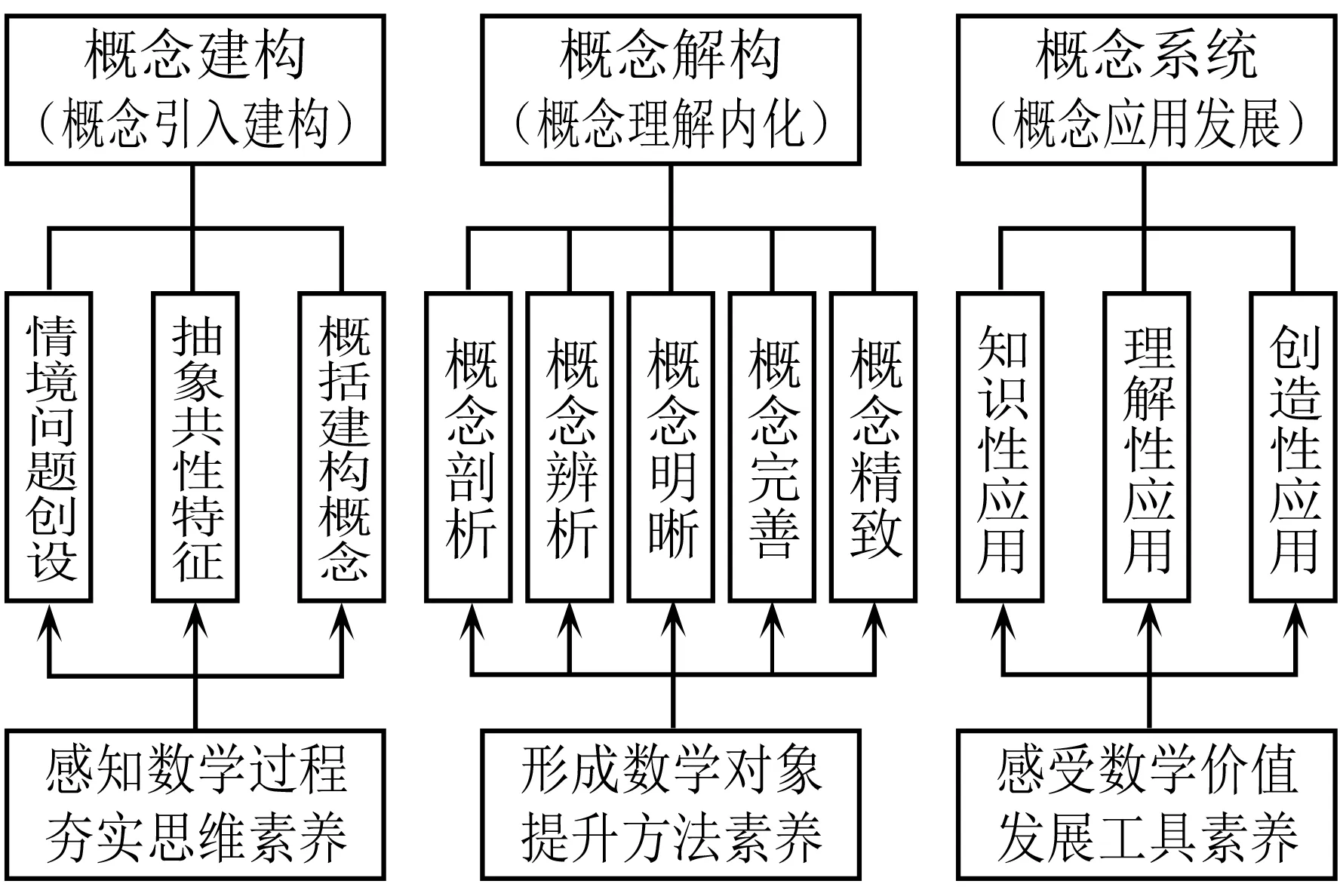
图1 数学核心概念教学的“三阶段十一环节”基本结构

(1)概念建构：这是数学核心概念教学的基础，它不是简单的概念同化或顺应，而是通过概念形成，从情境与问题中把握知识及其产生的原因；从共性特征的抽象中概括并建构数学核心概念．

(2)概念解构：这是数学核心概念教学的核心．只有充分解构概念，由表及里，通过概念剖析、辨析、明晰、完善和精致，将概念进行分解与重组、区别与联系、发展与提炼，才能准确把握数学核心概念的内涵本质，领悟内容所反映的思想方法．

(3)概念系统：这是数学核心概念教学的价值所在．基于对概念的充分理解，才能进一步建立基于数学核心概念的框架体系，在这一体系中对概念进行知识性应用、理解性应用，并最终实现创造性应用，建立基于数学核心概念的概念逻辑发展序列，把握知识间的多元联系，构建概念系统．

3 “三阶段十一环节”教学实践——以“等比数列”复习课为例

基于数学核心概念的“三阶段十一环节”教学基本结构，以“等比数列”复习课为例，进行具体教学实践探索．

3.1 概念形成建构概念，夯实数学思维素养

情境：已知数列{an},{bn}的通项公式分别为an=2n,bn=3n．

问题1{an},{bn}是等比数列吗？为什么？

问题2{anbn}是等比数列吗？为什么？

问题3等比数列是如何定义的？

设计意图创设问题情境，并通过层次递进的三问，立足具体实例，感知等比数列概念属性．虽然作为复习课，学生已经学习过等比数列的概念，但作为本节课的核心概念，还是需要创设情境，通过简单具体的实例，唤醒学生对等比数列概念的回忆及具象认知．进一步追问“为什么”，达到对等比数列概念的进一步思考，追究其概念共性特征的认知，引导学生再一次实践等比数列的概念建构过程．

3.2 理解内化解构概念，提升数学方法素养

问题4剖析并理解定义，如何证明一个数列是等比数列？

设计意图明确等比数列的数学表征方式，通过数学表征剖析概念，概念定义进一步数学化．

问题5如何证明一个数列不是等比数列？

设计意图基于不同概念的比较，辨晰概念．通过不是等比数列的证明，进一步认识等比数列定义中的“任意性”，明确对“任意性”的否定是举反例，寻找“存在”不成立情况的数学思维方式．

问题6联系等差数列，思考等比数列与等差数列的联系与区别．

设计意图基于同类概念的对比联系，明晰概念，突出概念的特有属性．即将等比数列与等差数列进行比较，两者定义相近，都是用运算定义数列；但两者的运算不同，前者是作比，后者是作差．在理解的过程中，就可以对数列概念进行深入理解——基于初等运算定义数列．

问题7类比等差数列，对等比数列还有哪些认识？

设计意图发展概念性质等，完善概念．完善概念的方式一般可借助同类概念的发展方式，如对概念的分类、性质、运算律等开展探讨．等比数列这一概念的完善，可借助等差数列的研究方式，对其运算性质进一步探索，为之后概念本质的挖掘奠定基础．

(1)数列内部的运算性质探究：例如，若m+n=p+q，则aman=apaq；若数列{an}为等比数列，则{can}(c为非零常数),{an+an+1}为等比数列等．

(2)数列之间的运算性质探究：例如，数列{an},{bn}为等比数列，则{anbn}为等比数列等．

问题8请归纳总结等比数列性质研究的一般方法．

设计意图挖掘概念本质，精致概念．在对等比数列性质的分类、归纳中发现：等比数列概念的发展无非是在数列内部或数列之间进行加、减、乘、除等初等运算去研究数列的“运算”特征，明确数列是以项数为自变量的离散函数本质．

3.3 应用实践概念系统，发展工具素养

问题9已知数列{an},{bn}的通项公式分别为an=2n,bn=3n，{an+bn}是等比数列吗？为什么？

设计意图概念的知识性应用．

问题10已知数列{cn}，其中cn=2n+3n，是否存在常数p，使得{cn+1+pcn}是等比数列？若存在，求常数p．

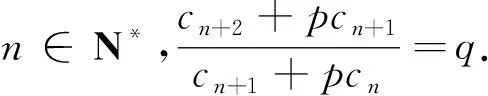
设计意图概念的理解性应用，即基于概念背后的技能、方法的灵活应用．本题发展于问题9的进一步探索，深化概念，形成思维路径．

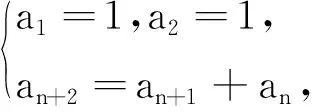
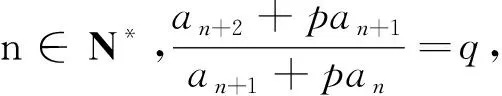
问题12能否由此结论进一步探索斐波那契数列的通项公式？

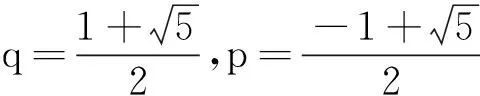
设计意图概念的创造性应用．以学生熟知的斐波那契数列为背景，唤起研究兴趣；以问题11搭建研究中间环节，并利用化归思想和等比数列求通项的方法，得到斐波那契数列通项公式．问题11这一中间环节的搭建与问题9、10具有同样的研究路径，可由教师搭建，更可由学生自行提出.这一组问题提供了(等比)数列研究方式在实际问题解决中的一般路径与方法，发展了学生解决问题的能力和素养．

问题13回顾等比数列学习过程，总结数列研究的一般路径与方法.

问题14思考面对一个陌生数列如何开展数列研究的一般方法.

设计意图总结思考，形成概念结构系统．回顾反思数列学习认知规律，把握数列概念作为研究基础的重要性；明确数列研究的一般方法——基于代数运算的研究，构建数列概念系统的认知结构．

4 小结

基于数学核心概念的教学基本结构研究，旨在以数学核心概念建构为起点，梳理数学知识逻辑发展的结构，并探索概念发展与运用的一般规律和方法．

概念的认识与理解是一个长期的、不断螺旋上升的过程，需要经历“事实—原理—结构—应用—观念”几个过程．本文在开展以上环节的实施过程中，高度重视核心概念原理解构中概念逻辑发展的结构：从概念剖析出发，通过不同概念比较辨析、同类概念联系明晰、发展概念性质完善概念，并在理解基础上精致概念．

基于数学核心概念的教学价值，在于其可不断生长发展的生命力．而概念生长发展的程度，也是评价概念解构过程是否充分完整的重要指标．

当然，基于数学核心概念的网络系统建构不是一蹴而成的，需要始终坚持基于数学核心概念的新课教学和复习课整合，在循环往复中动态建构．