名题恒久远 经典永流传*——2021年全国乙卷(理)第21题的源与流

陈熙春 (广西省宁夏六盘山高级中学 750002)

近年来的高考试题中,涌现了许多数学经典名题,其背景新颖、立意高远、设问巧妙，犹如一颗颗闪耀的明珠,璀璨夺目,形成了一道亮丽的风景线.2021年高考全国乙卷理科数学第21题的命题背景正是阿基米德三角形及其性质.

抛物线的弦与过弦的端点的两条切线所围的三角形通常称为阿基米德三角形.阿基米德三角形以其深刻的背景、丰厚的内涵产生了无穷的魅力.历经千年，阿基米德三角形仍然受到高考命题者的青睐．熟练掌握阿基米德三角形的基本性质,可以快速地解决相关问题,有利于帮助学生总结规律、拓展思维、提高能力.

1 真题呈现

例(2021年全国乙卷理科第21题)已知抛物线C:x2=2py(p>0)的焦点为F,且F与圆M:x2+(y+4)2=1上的点的距离的最小值为4．

(1)求p；

(2)若点P在圆M上,PA,PB是C的两条切线,A,B是切点,求△PAB面积的最大值.

分析 (1)根据圆的几何性质可得出关于p的等式，即可解出p的值.

(2)设点A(x1,y1)，B(x2,y2)，P(x0,y0)．利用导数求出直线PA与PB的方程，进一步可求得直线AB的方程,将直线AB的方程与抛物线的方程联立,求出|AB|以及点P到直线AB的距离,利用三角形的面积公式,结合二次函数的基本性质可求得△PAB面积的最大值.

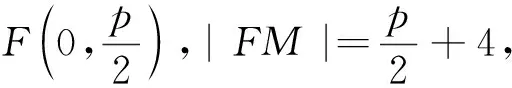
(2)思维角度1：利用函数思想转化为二次函数的最值问题.

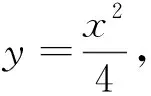
思维角度2：割补法.利用化归思想,利用中线对面积进行转化,把△PAB的面积转化为两个小三角形的面积之和．

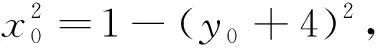
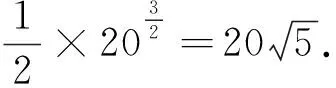
思维角度3：“算两次”思想.

解法3 从不同角度分别计算点P的坐标．

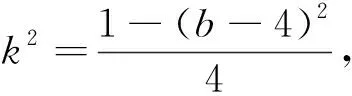
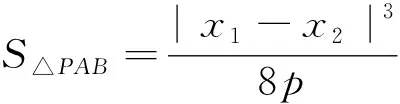
2 阿基米德三角形探究

阿基米德三角形的性质,以抛物线x2=2py(p>0)为例．如图1，抛物线上两个不同的点A，B的坐标分别为A(x1,y1)，B(x2,y2)，以A，B为切点的切线PA，PB相交于点P,我们称弦AB为阿基米德三角形PAB的底边．

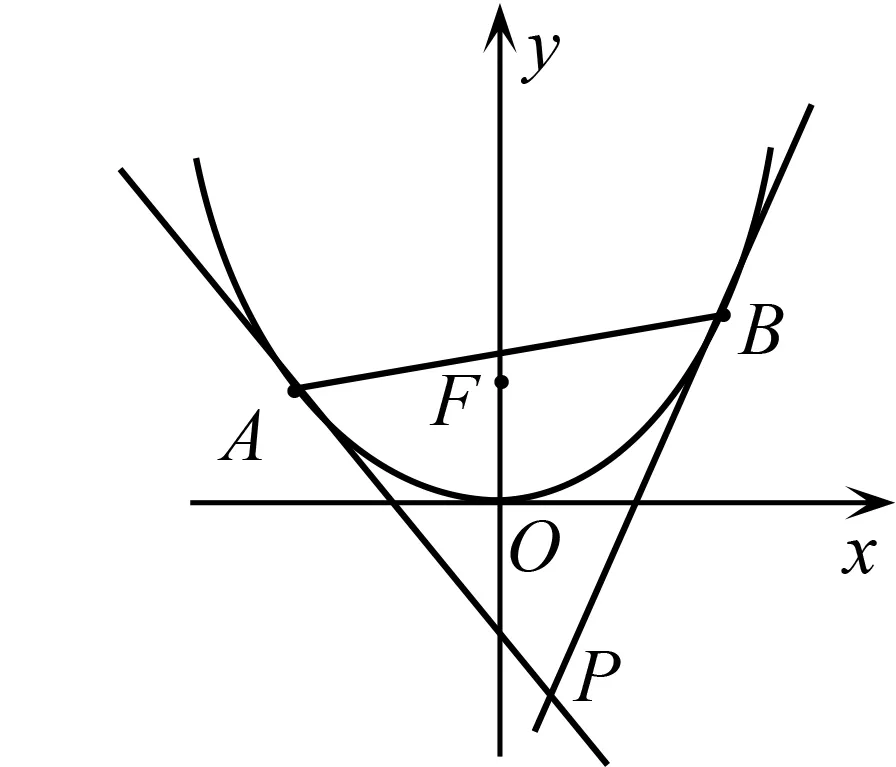
图1

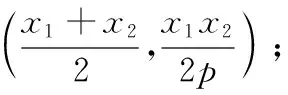
(2)底边AB所在的直线方程为(x1+x2)x-2py-x1x2=0．

(3)设点P的坐标为(x0,y0),则底边AB所在的直线方程为x0x-p(y-y0)=0．

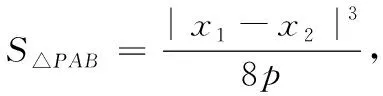
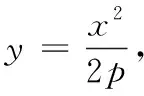
从而可得：阿基米德三角形底边上的中线平行于抛物线的对称轴．

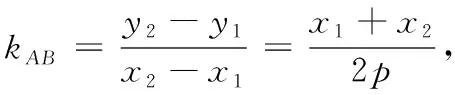
证法2 (同构法)易得直线PA的方程为x1x-py1-py=0，直线PB的方程为x2x-py2-py=0，又直线PA,PB经过点P(x0,y0),故x1x0-py1-py0=0，x2x0-py2-py0=0,则AB所在直线的方程为x0x-p(y-y0)=0.

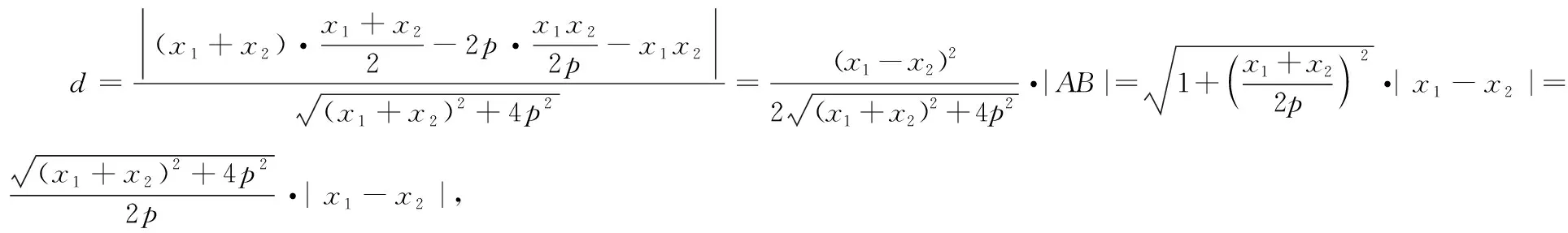
图2

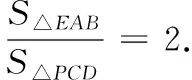
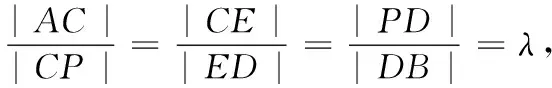
性质2若阿基米德三角形的底边(即弦AB)过抛物线内定点C(xC,yC)，则另一顶点P的轨迹为一条直线,其方程为xCx-p(y+yC)=0.

特殊地,当定点C在y轴上时，由性质2可得如下推论.

推论若阿基米德三角形的底边(即弦AB)过抛物线内定点C(0,m)(m>0)，那么

(1)另一顶点P的轨迹方程为y=-m；

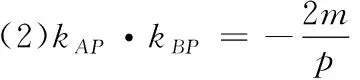
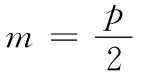
(4)AP⊥BP；(5)PF⊥AB；

(6)△PAB面积的最小值为p2.

下面只证明结论(6)．

性质3在阿基米德三角形中，∠PFA=∠PFB.

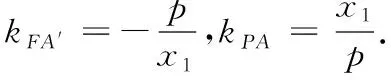
图3

同理可证|PB′|= |PF|,∠PB′B=∠PFB.所以|PA′|=|PB′|= |PF|.即∠PA′B′=∠PB′A′.

所以∠PA′A=∠PA′B′+90°=∠PB′A′+90°=∠PB′B,即∠PFA=∠PFB.

3 往年高考试题链接

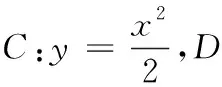
(1)证明：直线AB过定点；

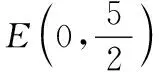
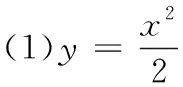
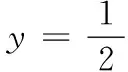
例2(2005·江西卷理第22题)设抛物线C:y=x2的焦点为F，动点P在直线l:x-y- 2=0上运动，过P作抛物线C的两条切线PA，PB，且与抛物线C分别相切于A，B两点.

(1)求△APB的重心G的轨迹方程；

(2)证明:∠PFA=∠PFB.

分析 第一问是典型的利用“相关点法”求动点轨迹方程的问题,先利用性质1求出点P的坐标，再利用点P与点G坐标之间的关系就可得出重心G的轨迹方程.第二问本质为阿基米德三角形性质3，可参考性质3的几何证法,具体解法略.

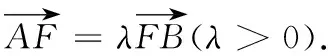
(2)设△ABM的面积为S，写出S=f(λ)的表达式，并求S的最小值.

例4(2008·山东卷理第22题)如图4，设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线，切点分别为A，B．

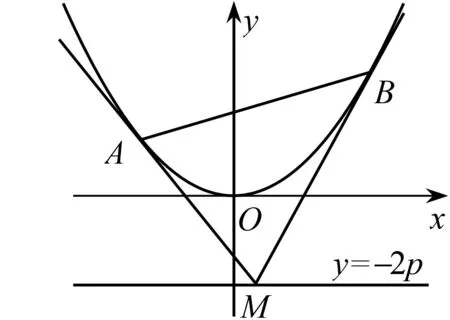
图4

(1)求证：A，M，B三点的横坐标成等差数列．

分析 第一问考查了阿基米德三角形底边上的中线平行于抛物线的对称轴这一性质.第二问考查了性质1中的底边AB所在的直线方程.第三问考查了阿基米德三角形中的坐标之间的关系.

例5(2007·江苏卷理第19题)在平面直角坐标系xOy中，过y轴正方向上一点C(0,c)任作一直线，与抛物线y=x2相交于A，B两点，一条垂直于x轴的直线分别与线段AB和直线l:y=-c交于P,Q．

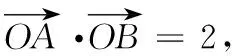
(2)若P为线段AB的中点，求证：QA为此抛物线的切线．

(3)试问(2)的逆命题是否成立？说明理由．

分析 第二、三问考查了抛物线的切线问题及阿基米德三角形底边上的中线平行于抛物线的对称轴这一性质．

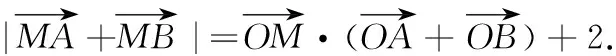
(1)求曲线C的方程．

(2)动点Q(x0,y0)(-2

分析 第二问考查了阿基米德三角形的面积问题,也可以用性质1的推论2来解决.

高考试题凝聚了众多命题专家的集体智慧,对中学教学起着“引导教学一面旗”的作用.对于如何高效地进行高考备考,高考试题具有极高的研究价值,可以达到博观而约取、厚积而薄发的目的.由阿基米德三角形改编生成的高考题还出现在2013年广东卷、江苏卷、辽宁卷,2006年重庆卷、湖北卷等.由此可见,历经千年的经典名题——阿基米德三角形,蕴涵着博大精深的数学思想方法,依旧焕发出勃勃生机,犹如星光璀璨的明珠,点缀着美丽的数学天空,闪耀着数学家智慧的光芒.真可谓“名题恒久远,经典永流传”.