问题引领 自主探究 自然建构——“两角和与差的余弦公式”教学设计和反思

孔帮新 (江苏省丹阳市第五中学 212300)

1 基本情况

1.1 授课对象

学生来自四星级普通高中重点班，基础较好，有一定的自学能力、推理能力及运算能力．

1.2 教材分析

所用教材为《普通高中课程标准实验教科书·数学(必修4)》(苏教版)，“两角和与差的余弦公式”为第3章“三角恒等变换”第1节内容，它揭示了单角正、余弦值与和、差角余弦值之间的内在联系，是在研究了同一个角的三角函数变换的基础上进行学习的，是诱导公式的推广，是后面推导两角和、差，倍角、半角等三角恒等变换公式的基础和核心，也是本章的重点和难点．教学中要引导学生在公式生成过程中体验式子中的角度变换、式子的结构形式变换以及不同三角函数之间的变换，领悟换元、化归、特殊与一般等思想方法，理解公式之间的内在联系，为熟练运用公式进行三角函数式的化简、求值、恒等式证明打好基础，发展推理能力和运算能力．

教学目标 (1)经历运用几何法推导出两角和与差的余弦公式的过程，体验、感受数学发现和创造的快乐；(2)能用两角和与差的余弦公式进行简单三角函数式的化简、求值．

教学重点 创设问题情境引导学生通过自主探究和合作讨论，推导出两角和与差的余弦公式．

教学难点 创设问题情境引导学生建构推导两角和与差的余弦公式的思路．

2 教学过程

2.1 自然引入

对于两角和与差的余弦公式的引入，我们以问题串形式形成如下设计方案：

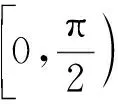
问题1在锐角范围内我们常用的特殊角有哪些？

问题2这些特殊角的三角函数值大家都很熟悉了，如何求cos 15°,cos 75°？

问题3由于15°=45°-30°=60°-45°， 75°=30°+45°，那么cos 15°=cos(45°-30°)= cos 45°-cos 30°成立吗？你能检验吗？cos 75°=cos(30°+45°)=cos 30°+cos 45°成立吗？你能检验吗？

学生根据知识的负迁移得出错误结论，在教师的指导下学生合作交流，很自然地得到cos(45°-30°)≠cos 45°-cos 30°，cos(30°+ 45°)≠cos 30°+cos 45°．

问题4cos 15°,cos 75°与30°,45°,60°的三角函数值有什么关系？

问题5更一般地，cos(α+β)=？cos(α-β)=？cos(α+β),cos(α-β)与角α,β的三角函数有何关系？

通过创设问题情境自然地提出问题，引发学生积极地思考，从而很顺畅地引入研究的课题，这样有利于激发学生强烈的求知欲望，使学生目标明确、迅速进入角色．这种设计更符合学生的认知规律以及两角和与差公式产生的过程．

2.2 自主探究

(1)探究点1：如何自主地在直角坐标系中作出α+β,α-β？

为了设计得更自然，我们以问题串的形式进行如下设计：

问题6我们研究任意角三角函数和诱导公式都是借助于直角坐标系和单位圆研究的，那么如何研究两角和与差的三角函数呢？

问题7我们将角α,β分别放在两个直角坐标系中(图1、图2)，将角β拿出来，在第一个坐标系中如何作出α+β？(让学生上黑板用道具进行拼接)有几种拼接方案？(图3、图4)

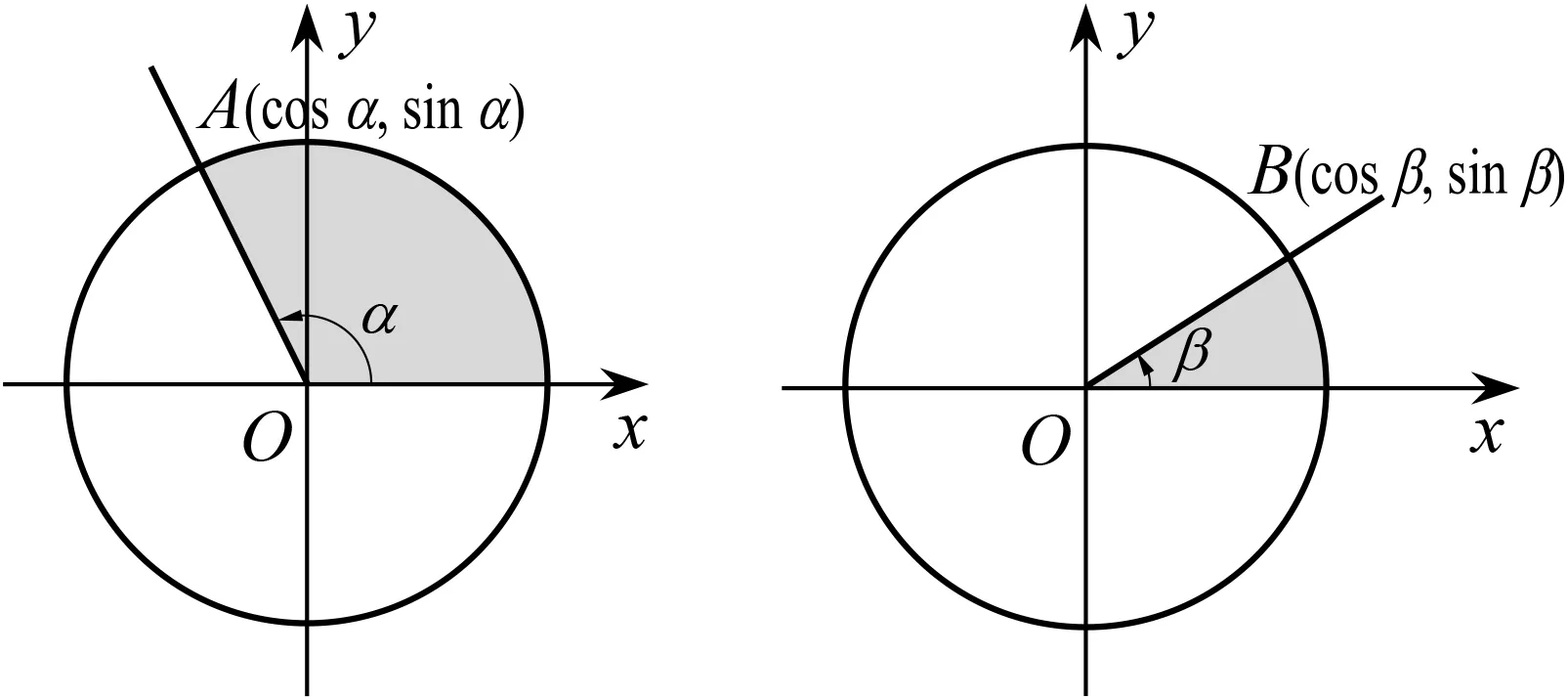
图1 图2

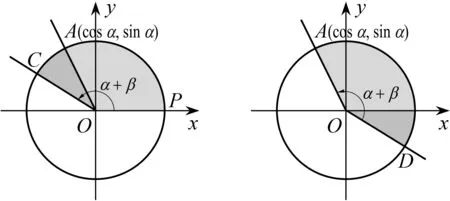
图3 图4

问题8第一种拼接方案中(图3)，α+β的始边与单位圆的交点P的坐标是什么？α+β的终边与单位圆的交点C的坐标又是什么？

问题9第二种拼接方案中(图4)，角α的终边与单位圆的交点A的坐标是什么？角-β的终边与单位圆的交点D的坐标是什么？

问题10我们将角α,β分别放在两个坐标系中，将角β拿出来，在第一个坐标系中如何作出α-β？(让学生上黑板用道具进行拼接)有几种拼接方案？(图5、图6)

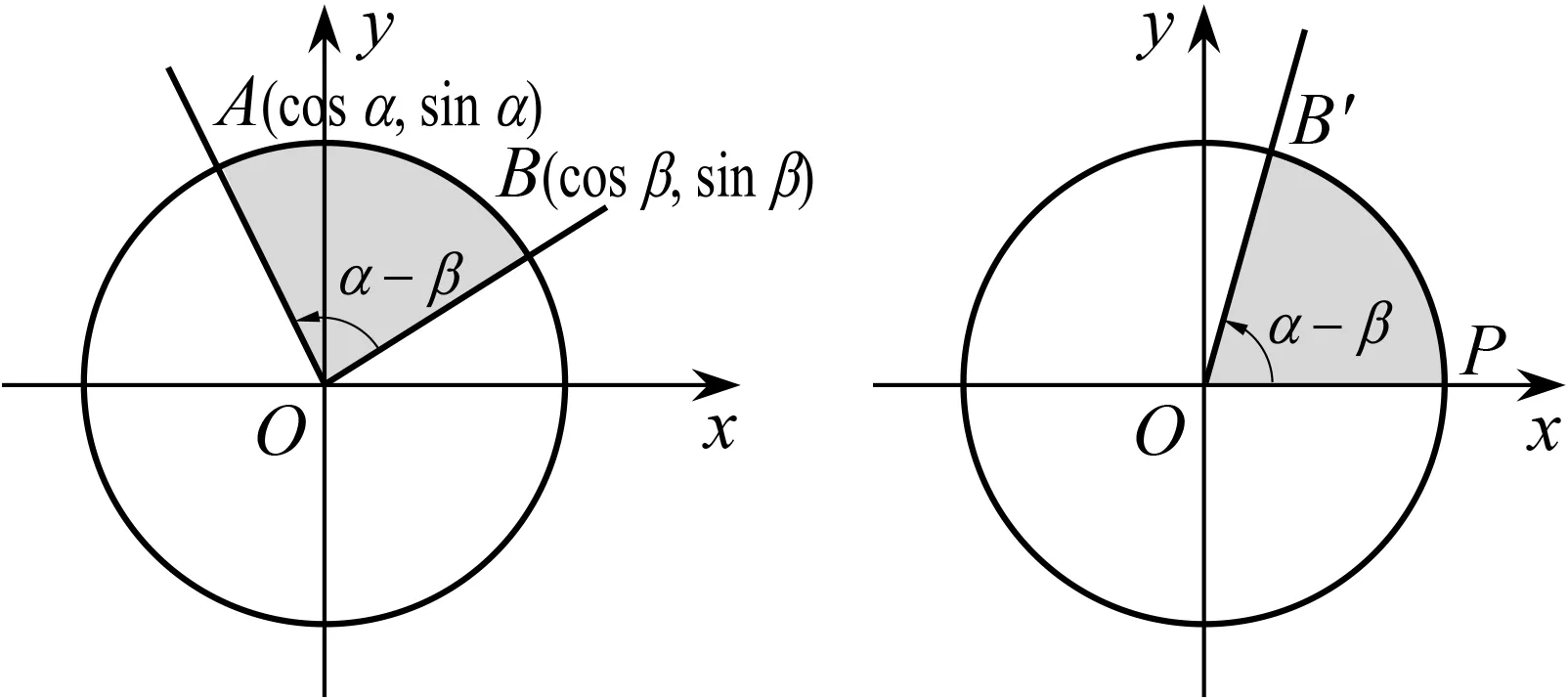
图5 图6

问题11第一种拼接方案中(图5)，角α的终边与单位圆的交点A的坐标是什么？角β的终边与单位圆的交点B的坐标是什么？

问题12第二种拼接方案中(图6)，α-β的始边与单位圆的交点P的坐标是什么？α-β的终边与单位圆的交点B′的坐标又是什么？

将两个角分别作在两个直角坐标系里，这个设计简单自然，是本节课设计上的一个创新，它使得学生不受其他图形的干扰，通过道具演示拼接好两种情况，从而很轻松地作出α+β,α-β，再加屏幕展示清晰直观，整个教学过程自然流畅．

(2)探究点2：如何自主地寻求到等量关系？

观察图形，我们先探究α+β的三角函数与角α及角β的三角函数的等量关系.为了使学生更自主地寻求到等量关系，我们设计如下问题串：

问题13观察两个图形，你们能发现什么等量关系？

问题14观察两个图形，两个等圆中，由圆心角相等能得出什么等量关系？

问题15这几种等量关系中，哪种等量关系能用坐标的形式表示出来？并且坐标中含有角α+β的三角函数与角α,β的三角函数．

寻求等量关系是这节课的难点，也是关键之所在，多次试讲都发现学生不知如何找到等量关系，如何突破？首先我们设计将两条线段分别放在两个单位圆中，这种简单自然的创意可使学生不受其他图形干扰，使学生更易找到线段的等量关系；其次教师提出更具启发性和目标性的问题也是促使学生更容易地找到等量关系的关键．通过以上设计，学生很快就能找到最有用的等量关系，即PC=AD，然后将其坐标化即可．

2.3 自主建构

为了再现公式发现的“再创造”过程，我们让学生上黑板进行板演，共同发现公式的产生过程.为了让学生自主生成公式，我们设计如下问题串．

问题16两角和的余弦公式是什么？

问题17上面两个图形所画的角都在[0,π)内，而且α>β，那么对任意的角α,β，上述公式是否成立？

我们可以引导学生自主地讨论四种情况：(1)α在[0,π)内，β在[π,2π)内；(2)β在[0,π)内，α在[π,2π)内；(3)α,β都在[π,2π)内；(4)α,β都大于2π.经过学生自主探究，运用诱导公式将角都转化到[0,π)内，从而证明在四种情况下两角和的余弦公式都成立．

再引导学生对所涉及的角进行推广，使公式的得出具备一般性．

问题18大家想一想，我们得到了两角和的余弦公式，对于两角差的余弦公式还需不需要再去进行这种重复的运算？

问题19两角和的余弦公式与两角差的余弦公式之间有什么转化关系？

问题20两个公式的特点是什么？

归纳公式结构特点，给出记忆口诀：CCSS，符号相反．

得到两个公式后我们再引导学生发现两个公式之间的转化关系，即用-β代换β，这有利于学生在大脑中进行公式的自主建构．最后由公式特点归纳出记忆口诀，简单自然，琅琅上口，易于学生记忆．学生在“自主生成、自主探究”的课堂中自主建构了两角和与差的三角函数公式．

2.4 自主应用

问题21现在你能求出cos 15°,cos 75°了吗？

前后呼应，运用公式解决问题，让学生亲身体会获得成功的喜悦！问题的解决是公式的简单正用．

例题设计：

1.计算：cos 80°cos 20°+sin 80°sin 20°．

变式 (1) cos 80°cos 20°+sin 80°cos 70°；(2) cos 80°sin 70°+sin 100°sin 20°．

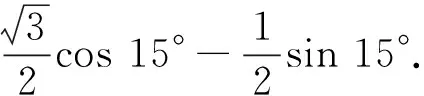
3.计算：cos215°-sin215°,推广至一般情况cos2α-sin2α=cos 2α．

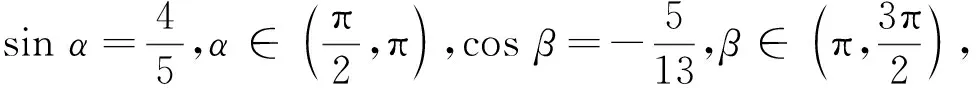
例题的设计意图：第1题的两个变式和第2题，让学生初步体会公式的逆用和变形；第3题推广到一般情况为后续学习做好铺垫；第4题中的正负取舍是学生的易错点．

通过层层深入的例题与习题的配置，引导学生积极思考，自主解决问题，使学生从“懂”到“会”再到“悟”，并将所学知识纳入到新的知识体系中．

2.5 自主总结

课堂小结是在教师的指导下，由学生自主归纳：(1)数形结合推导出两角和与差的余弦，两个公式之间可以相互转化；(2)两角和与差的余弦公式为cos(α±β)=cosαcosβ∓sinαsinβ，记忆口诀为“CCSS，符号相反”；(3)公式的灵活运用；(4)通过本节课的学习，掌握了一些探究数学问题的基本方法．

自主总结可以使学生加深对公式和推导过程的理解，并明确学习本节课所要达到的教学目标．

3 回顾与反思

3.1 设计思路

(1)公式推导思路的设计

由于和、差、倍角的三角函数之间存在着内在的联系，可以选取一个基础公式来推理得到其他公式，这不是唯一的.教材之所以选用两角差的余弦公式作为基础，是缘于向量工具的提前引入，但现在面对的学生没有学习向量，所以选择几何法证明两角和与差的余弦公式，而用几何法推导两角和的余弦公式和两角差的余弦公式所用的方法是一样的，基于此，我们选择将两角和的余弦公式的推导作为本节课的教学重点．

(2)本节课引入的设计

根据已学的知识引出新问题，然后抛给学生，让学生探究，学生大胆猜想，后又自主探究推翻猜测，教师适时引导，两角和与差的余弦公式究竟是什么？这就非常自然地引出本节课需要探究的问题．通过问题情境的设置，使学生思维迅速处于“愤”“悱”状态，产生强烈的求知欲望，积极主动地投入学习．

(3)突破公式推导难点的设计

我们没有让学生对在直角坐标系里的单位圆中是作出α+β还是α-β作选择，而是让学生既作出α+β又作出α-β．但如何让学生比较自然地作出α+β和α-β并且能非常容易地寻求到等量关系是本环节的一个难点．我们将角α和β分别放在两个直角坐标系中，将角β拿出来，此处借助道具让学生拼接，迅速找到作出α+β和α-β的两种方法，并且用课件的形式分别呈现在两个单位圆中，然后由教师提出具有启发性和目标性的问题，以便学生更容易地找到等量关系，至此难点一步步得到化解．在推导过程中，重点引导学生推导两角和的余弦公式，对于两角差的余弦公式可以同理得到．得到两个公式后引导学生发现两个公式之间的转化关系．至此难点逐一得以突破．

3.2 教学反思

(1)课堂教学要通过设计教学主线推进教学进程

基于整章教学要求的考虑，本节课将“两角和的余弦公式的探究”作为课堂教学的明线，核心指导思想——转化思想作为一条暗线来推进课堂教学．本节课一开始就让学生求15°和75°的余弦值，学生就能想到转化为特殊角去处理．在后面公式推导的过程中，通过设计问题串引导学生在参与公式推导的探究活动中，深刻体会未知角向已知角的转化，体会未知值向已知值的转化以及未知范围向已知范围的转化等，切实理解公式产生的来龙去脉、结构特征与内在联系，从而有助于学生熟练、灵活地驾驭公式，切实提高课堂教学的有效性[1]．

(2)课堂教学要引导学生通过多种思路探究公式

本节课由于面对的学生没有学习向量知识，所以只能选择几何法证明两角和与差的余弦公式，并且选择了两角和的余弦公式证明作为本节课的重点，这是本节课在公式推导方面的一点遗憾．如果学习了向量，则可以通过代数法(向量法)和几何法推导出两角和与差的公式，两种推导方法(代数与几何)相得益彰，充分凸显向量方法的工具作用，让学生在公式的推导和探究过程中体验、感受数学发现和创造的快乐，体会向量和三角函数间的联系，从而有效地培育学生的数学思维能力和数学核心素养．

(3)课堂教学要指导学生自主总结探究问题的方法

通过本节课的学习，我们也要为学生归纳总结出一个探究问题的思路和方法：①善于运用已学过的知识，将研究的新问题转化为已学过的知识进行处理和解决；②知识体系建构要由浅入深、循序渐进、逐步推进，由学生自主探究、自主建构自己的知识体系．我们认为这种探究数学问题的方法符合学生的认知规律．后续新公式的探究就可以放手让学生去自主探究，这对学生自主建构公式网络体系、培养自学能力给予了很好的方法上的指导，这才是本节课教学中最应该让学生掌握的东西．