铸坯质量预测的混合式特征选择方法

程芳明 容芷君 但斌斌 刘洋

（1：武汉科技大学冶金装备及其控制教育部重点实验室 湖北武汉430081；2：武汉科技大学机械传动与制造工程湖北省重点实验室 湖北武汉430081；3：宝钢股份中央研究院 湖北武汉430080）

1 前言

在连铸生产中，及时在线预报和检测铸坯质量，对确保生产的连续性、提高产品质量及降低生产成本具有重要的意义［1］。目前对铸坯质量预测的研究主要有专家系统、统计学分析、数据分析等方法，但由于在连铸生产过程中影响连铸坯质量的环节众多，各因素之间的耦合作用，使得铸坯质量预测精度不高，质量缺陷问题得不到有效改善［2-3］。随着大数据时代的到来，数据挖掘因其及时性、智能性、极强的大数据处理能力逐步成为预测铸坯质量及提高预测精度的主要方式。

当前已有众多研究通过数据挖掘方法预测铸坯质量，将生产过程中涉及的影响因素作为模型的输入特征，采用模糊识别［4］、神经网络［5-7］、随机森林［8］等模型实现铸坯质量的预测。这些研究是根据冶金原理分析影响铸坯质量的因素，将其作为预测模型的输入特征，虽然可以提取用于预测的所有信息，但炼钢是一个非常复杂的过程，且影响机理复杂，这使得铸坯质量与各影响因素间具有非线性和不确定性关系，所以通常会得到无关特征和冗余特征。无关特征和冗余特征的存在会极大影响模型的预测准确率与算法效率，因此，选用合适的特征选择方法对特征进行处理，能有效提高预测精度与效率。

本文提出一种混合式特征选择方法，首先采用融合互信息的最大相关最小冗余特征评价函数对原始特征集进行筛选，剔除部分不相关特征和冗余特征，减少特征的个数，得到特征子集S；然后采用递归特征消除法与随机森林相结合的包装式精选方法，考虑特征组合对分类性能的影响，使用随机森林分类器的分类性能来评价特征子集，同时得到当前特征子集中每个特征的重要性，并使用递归特征消除法从特征子集S开始，以最小化铸坯夹杂缺陷的分类错误率为目标，每次剔除重要性较小的一个或几个特征；最后选择分类错误率最低的特征子集作为最优特征子集。

2 构建原始特征集

2.1 铸坯质量问题分析

针对铸坯质量的预测与控制，各大钢铁企业先后开发了许多应用系统。如传统的离线检查冷态铸坯质量、基于冶金原理的专家系统等，但随着连铸坯的质量要求越来越高这些方法已经远远不能适应当下工艺和质量的要求，因此利用铸坯生产过程中的数据对铸坯质量进行分析对于钢厂来说是非常重要的。某钢厂2020年2月至6月铸坯质量缺陷统计结果如表1所示，可知夹杂发生的频率最高，达到62.6%，是该钢厂最常见的质量缺陷，因此本文以夹杂缺陷为例。

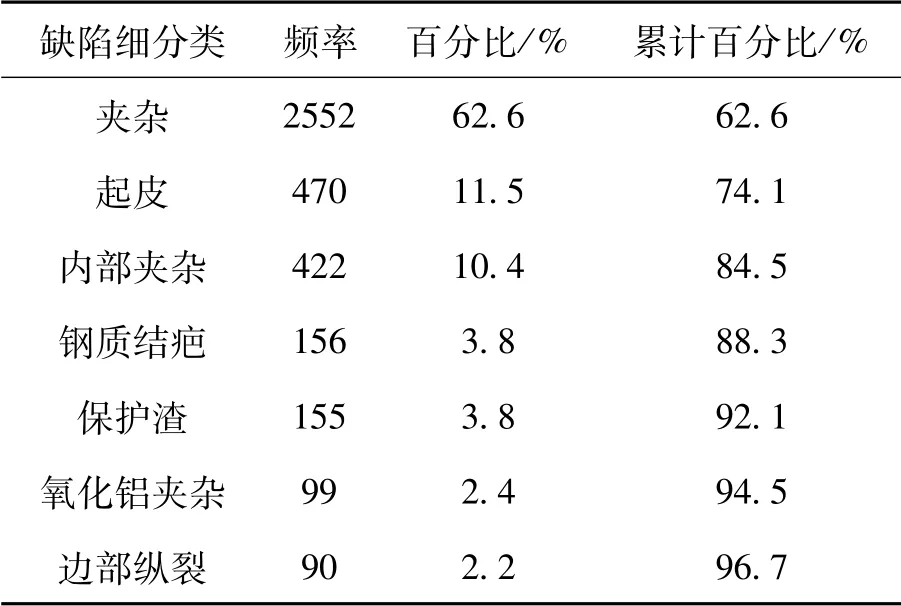
表1 某钢厂2020年2月至6月铸坯质量缺陷统计

2.2 构建铸坯质量原始特征集

收集某钢厂2020年2月至6月共5个月的生产数据，提取有铸坯夹杂质量缺陷的2552条数据，考虑到数据采集的滞后性，同时选取未出现质量缺陷的2291个样本作为对照，最终得到包含4843个样本的数据集。首先删除数据集中与夹杂缺陷明显无关的记录，例如熔炼号、日期等，然后根据对夹杂缺陷成因的相关研究，同时结合专家经验，最终确定夹杂质量缺陷的21个影响因素，构成铸坯质量预测原始特征集，如表2所示。最终数据集共包含22列，其中有21列为特征，剩余一列为铸坯质量分类标签，其包含“正常”和“夹杂”两种类别。为了后续分类任务，采用数值化编码的方式对字符型特征预处理，然后利用Z-Score标准化消除量纲的影响。

表2 铸坯质量原始特征集

3 混合式特征选择方法

对于无关特征和冗余特征对分类任务的干扰，大多数研究采用特征选择方法来解决。常见的特征选择方法分为过滤式、包装式和嵌入式［9］。包装式需要多次训练模型，得到的特征子集性能最好，但时间复杂度较高；嵌入式将特征选择与机器学习算法训练放在同一过程中进行，特征子集性能比包装式差，但时间复杂度较低［10］；过滤式不依赖于特定的机器学习算法，直接对特征的相关性和冗余性进行度量，运行效率最高，但特征子集的性能较差［11］。

针对铸坯质量预测问题中特征冗余性强、关键特征不显著的特点，并综合考虑现有的特征选择方法，提出一种混合式特征选择方法，方法的主要流程如图1所示。该方法包括预筛选和精选两个过程，在预筛选中，使用互信息对特征的相关性和冗余性进行度量，并使用融合互信息的最大相关最小冗余特征预筛选函数，从而在特征选择过程中综合考虑特征的相关性和冗余性，剔除特征的相关性和冗余性，同时减少精选阶段的计算规模；在精选阶段，使用基于RFE-RF的包装式特征选择方法，考虑特征的组合对分类性能的影响。经过预筛选和精选，可以得到高相关低冗余的最优特征子集，同时保证该特征子集具有较高的分类性能。

图1 混合式特征选择方法框架图

3.1 基于互信息的过滤式预筛选方法

对于过滤式，特征与铸坯质量分类标签间的相关性越强，该特征越重要；特征与特征间的相关性越强，则两个特征的冗余性就越强，即这两个特征越不应该被同时选择进入特征子集。因此，在过滤式预筛选中，最关键的是找到一种合适的指标来度量相关性。考虑到炼钢过程的复杂性，本文使用互信息（MI）来衡量特征与铸坯质量分类间标签以及特征与特征间的相关性。对于任意两个变量和，其互信息定义为：

文献［12-13］中提出了一种最小冗余最大相关算法（mRMR），该算法通过设置特征评价函数，对特征的最大相关和最小冗余进行定义。基于该算法，本文提出融合互信息的最大相关最小冗余特征预筛选评价函数，令原始特征集为X＝{xi｜i＝1，2……，21}，铸坯质量分类标签为Y，函数定义如下：

式中：x—特征，且x∈X；

Ic（xi，Y）—特征与铸坯质量分类标签间的互信息值；

S—已选的特征子集；

Ir（xi，xj）—特征与特征间的互信息值，i≠j。

使用预筛选评价函数进行特征选择的过程如图2所示：

图2 特征预筛选过程

3.2 基于RFE-RF的包装式精选方法

包装式直接考虑的是特征子集的分类性能，通过迭代的过程，精选出使模型性能最优的特征组合作为特征子集。该方法得到的特征子集的分类性能较好，但一般要结合相应的子集搜索策略，因为特征组合的种类很多，且每种特征组合都需要训练分类模型进行验证，计算量将非常庞大。为此，本文提出基于递归特征消除法（RFE）-随机森林（RF）的包装式精选方法，该方法以最小化分类错误率为目标，使用RF分类器的分类性能来评价特征子集，同时得到当前特征子集中每个特征的重要性，并使用RFE作为每次迭代过程的特征子集更新方法，从特征子集S开始，每次固定剔除重要性较小的一个或几个特征，最后选择分类错误率最低的特征子集作为最优特征子集。使用RF进行分类的同时，可以得到当前特征子集S中每个特征的重要性评分，这是由于RF算法是一种基于bagging的集成分类器，由多棵完全生长的决策树组成，每棵决策树的训练集由自助重采样产生，即从样本数量为N的原始训练集中，有放回地重复随机抽取N个样本。因此，有的样本可能会多次被抽取，而有的样本则可能不会被抽取，这些不被抽取的数据构成了袋外数据（OOB data）。对袋外数据的某个特征的值进行扰动，通过扰动前后分类错误率的变化来度量该特征的重要性，计算方式如下：

该方法的过程如图3所示：

图3 特征精选过程

4 结果与实验对比

4.1 特征预筛选

对表2中的21个特征，计算这些特征与铸坯质量分类标签间及特征与特征间的相关性值，得到结果如图4所示。由图4（a）可知，“结晶器渣类型”、“长水口厂家”、“精炼方式”、“废钢加入量”这4个特征与铸坯质量分类标签间的相关性值大于0.2，相关性较高。图4（b）可以看到，“最低拉速”与“最高拉速”的相关性值为0.98、“铸机号”与“结晶器渣类型”的相关性值为0.65、“铸机号”与“断面宽度”和“断面宽度”与“结晶器渣类型”的相关性值为0.62，这些特征之间的冗余性较大。

根据相关性计算结果，结合特征评价函数，完成特征预筛选过程。由图2知，需要先指定要选择的特征个数k。因为第一个被选中的特征是相关性最大的特征，所以不管k取何值，根据评价函数，待选特征进入特征子集的顺序是相同的。图5给出了k取21时，每次进入特征子集的一个特征对应的评价函数取值。开始时特征子集S中没有特征，第一个进入特征子集S的特征为“结晶器渣类型”，此时特征评价函数的取值即“结晶器渣类型”与铸坯质量分类标签的相关性值，由图4（a）可知为0.473。第一个特征进入后，后续特征再进入特征子集时，特征评价函数综合地考虑特征与铸坯质量分类标签间的相关性以及该特征与特征子集中已有特征间的冗余性。特征评价函数的取值不断减小，是因为相对前面进入的特征，后面进入的特征其相关性较小而冗余性较大，直到“钢水节奏”这个特征进入特征子集时，特征评价函数取值为负，表明该特征对已选特征子集来说，其冗余性已经大于相关性，而后续再进入的特征，评价函数的取值进一步减小。综合上述分析可知，应该选择使得特征评价函数取值大于零的特征，即为“结晶器渣类型”、“长水口厂家”、“精炼方式”、“废钢加入量”、“温度是否合格”、“罐况”、“拉速落差”、“浇铸周期”、“水表号”、“断面宽度”、“配水方式”、“中包炉序”，共12个特征。

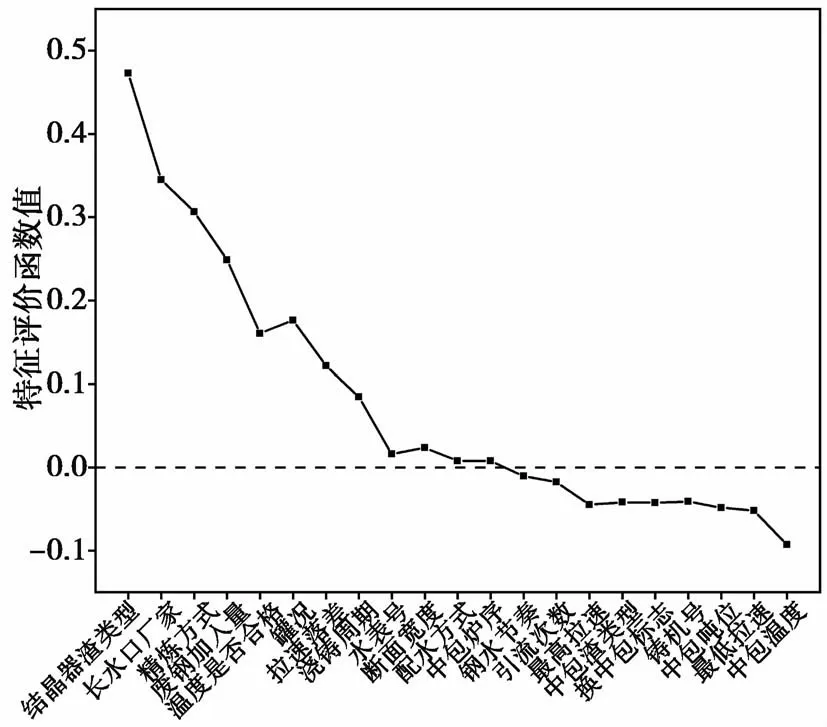
图5 特征评价函数取值变化

4.2 特征精选

在RFE-RF的特征精选中，使用特征子集更新算法RFE和随机森林分类算法RF，这两个算法都需要设定相关的参数。对于RFE算法，需要设置每次迭代时剔除的特征个数n，其决定了算法的计算规模，因为经过预筛选后仅剩12个特征，所以该参数设置为1即可。对于RF需要设置的参数包括决策树的个数a和每棵树分类时选用的最大特征数，考虑到共有4843个数据样本，a设置为100即可，而每次迭代特征的个数都不一样，所以将b设置为当次迭代时特征的总个数。每次训练分类器时，随机将4843个样本中的70%划分为训练集，剩余30%为测试集。图6显示了随着特征的剔除，随机森林分类器在测试集上错误率的变化。开始时，随着重要性较小的特征的剔除，分类错误率逐渐降低，而当重要性较大的特征被剔除时，分类的错误率随之增大。当剔除“水表号”、“浇铸周期”、“中包炉序”、“配水方式”、“罐况”、“废钢加入量”这6个重要性较小的特征时，分类的错误率最小，为9.8%，因此最终选择的特征为“精炼方式”、“断面宽度”、“拉速落差”、“温度是否合格”、“长水口厂家”、“结晶器渣类型”，共计6个特征。

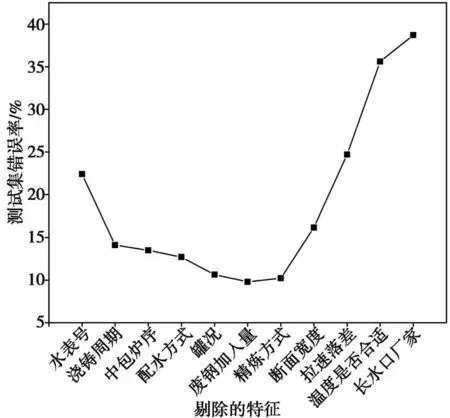
图6 随机森林分类准确率变化

4.3 分类效果比较

为了验证混合式特征选择方法在铸坯质量预测问题中进行特征选择的有效性，本文用随机森林分类器的分类错误率来评价该方法选取特征子集的优劣，对过滤式、包装式和混合式特征选择的效果进行比较，如表3所示。可以看到采用混合式特征选择方法选出的特征子集的分类错误率为9.8%，分类错误率比过滤式降低了13.5%，比包装式降低了8.2%，更好地达到了降低分类错误率的目的。

表3 4种特征处理方式下的分类错误率比较

5 结论

本文提出的混合式特征选择方法，首先在过滤式预筛选过程中充分考虑特征和铸坯质量分类标签之间的相关性和冗余性，避免了将无关特征引入模型，同时降低特征间的冗余性；然后在包装式精选过程中进一步考虑特征组合对铸坯质量分类效果的关联影响，进而提高模型的准确率。通过不同特征处理方法的对比，与采用单一的过滤式和包装式相比，混合式特征选择方法的分类错误率最低，证明了在铸坯夹杂质量预测问题中，本文所提出的混合式特征选择方法的优越性。