基于“构造法”的高中数学解题思路

吴延宝

(湖南长沙市长郡梅溪湖中学 410000)

高中数学相较于其他学科来讲，其难度非常高，这一设置主要是为了提升学生的数学能力，使学生的思维能够得到锻炼.但是因为难度过高，导致学生在解题的过程中，经常会出现各种错误，长时间发展，不仅无法帮助学生掌握更多的数学知识，而且还会使其失去学习的兴趣.通过构造法的利用能够有效解决这一问题，其在数学学习中能够进一步发挥出实际效果，帮助学生找到合适的解题方式，进而提升解题速度，使学生的综合能力获得更大程度的提升.为了使构造法能够发挥出更好的效果，需要针对其实际利用方式展开综合性的分析，借此使高中数学学习更加简单.

一、高中数学解题中构造法的概述

1.函数构造法的概念

数学发展的最早期，阿基米德等数学家在解决问题的过程中，就已经利用了构造法.在上个世纪中期，构造法受到了较高的重视，逐渐衍生出了现代意义的构造法.在现代数学思想之中，构造法指的是在解决数学问题过程中，因为问题的条件很难通过推导获得答案，所以就需要构造出一定的条件，使结果能够更加简单的解答出来.在构造法概念的角度来讲，很多数学家对其做出了定义，认为其属于一种通过固定方式经过一定的步骤，就能够获得结果的解题方式.简单来讲，在高中解决问题的过程中，学生基本上是按照题目所提供的思路继续向下解题.但是这一方式在面对一些问题的过程中，并不能发挥出比较好的效果.而这一情况下，就需要从其它角度改变自身的思维方式，使其中的难点不会对解题产生影响.相较于正常的逻辑方式，构造法是一种完全与众不同的思维方式，学生在解决问题的过程中，需要拥有更强的思维能力和观察力，才能够使其发挥出更好的效果.

2.构造法的应用价值

在高中数学解题的过程中，利用构造法能够获得非常好的效果，其主要体现在两个方面.首先是其可以使教师在讲解相关知识的过程中，更好的集中学生注意力，因为传统教学方式需要按照步骤进行讲解，所以会导致学生浪费大量的时间，而通过构造法解决相关问题，教师则可以利用其它方式展现出其中的内容，可以使学生在了解其之后，进一步提升自身的解题有效性.其次是在利用构造法解决高中数学问题的过程中，需要让学生认识到怎样能够有效的改变题目内容，并将构造法利用其中，其对于学生创新能力的发展具有一定的帮助.而且在使用构造法的过程中，可以使学生更加积极主动的进行思考，进而找到正确的解决方式，对于学生的发展来讲，具有非常积极的意义.

3.函数构造法的原理

数学相较于其他学科来讲，会更加的抽象，高中数学作为中学学科中较为难理解的一门学科，其中经常会出现一些通过正常方式无法解决的问题.而在这一情况下，构造法则通过逆向思维解决相关问题，使复杂问题简单化.通过结合题目中所提供的所有条件，从学生自身实际情况的角度出发，理解题目中的所有信息并获得结论.找到解决问题的所有条件，进而针对性的获得解决思路.构造法实际上就是将抽象的问题处理成简单的问题，借此找到合适的解题思路，并在这一基础上将其有效解决.在高中数学学习的过程中，为了使学生解题能力能够获得提升，经常需要反复练习相同类型的题目，在这一过程中，会使学生利用相同的思维模式解决本质相同的问题，使学生形成固定的思维模式，进而导致其无法有效找到其他的解题思路，解题效率明显下降.构造法的重点在于建立未知数与已知条件之间的联系，借此找到全新的解题思路，并降低固定思维模式所带来的影响.

二、高中数学解题中构造法的应用策略

1.构造函数

例1根据不等式，求出Y的范围：(Y2-2)3-Y3+2Y2-2Y-4>0.

分析该不等式中，最高幂为立方，而解决这一问题的重点则是Y的范围，从不等式中能够了解到，通过移项之后能够确定(Y2-2)3+2(Y2-2)>Y3+2Y，构造函数f(t)=t3+2t，将原本的不等式转变为f(Y2-2)>f(Y)，f(t)为增函数，所以Y2-2>Y，最终可得Y<-1或Y>2.

函数是高中非常重要的知识之一，其也属于高中数学的难点.在实际学习中，学生需要掌握相关的知识，在这一基础上，才能够了解具体的解题方式.从案例1可知，其主要是通过进一步理解问题中所涉及到的内容，利用函数本身的特点，形成合适的函数，将不等式转变为函数性质的利用.借助这一方式能够使学生的解题水平进一步提升，而且还可以帮助其获得锻炼.但是在实际使用这一方式的过程中，也需要注意一定的问题，例如数学题型种类很多，所以可能很难找到最关键的问题.在部分问题之中，解题过程会分为多个部分，所以在哪一部分中能够利用方式，就需要通过学生的分析才能够最终确认.

2.构造方程

在高中数学解题的过程中，构造方程法是一种非常常见的解题方式，而这一方式也能够对学生的知识掌握情况做出准确的把控.函数与方程之间的关系非常紧密，很多题目都可以通过函数与方程的结合获得最终答案.在利用构造方程法的过程中，实际上就是在原本已经获得的条件基础上，构建等量方程，借此使题目更加简单，通过这一方式提升解题效率.

例2在等式(m-n)2-4(n-x)(x-m)=0的基础上，证明m、n、x为等差数列.

从这一题目的角度来讲，如果使用正常方式进行解题则会使其难度进一步提升，需要通过大量的计算之后，才能够获得最终的结论.而在这一过程中，就可以通过构造方程法解决相关问题.在解题的过程中，将结论作为已知条件对其进行分析，将其与前一等式相结合，将问题简化，借此获得最终结论.

解构造方程式(n-x)t2+(m-n)t+(x-m)=0，并且令F(t)=(n-x)t2+(m-n)t+(x-m).

从题目中能够得出，F(1)=0，进而能够确认的是(n-x)t2+(m-n)t+(x-m)=0的实数根相等，最终获得t=1.所以方程的实数根都是1.按照韦达定理，能够获得m+n=2x.所以m、n、x为等差数列.

在这一解题过程之中，最重要的一项就是怎样利用构造法，将原本复杂的问题化为简单的问题，借此使解答过程更加快速与有效.

3.构造图形

除了构造方程和构造函数之外，高中数学解过程中，还会通过构造图形的方式进行解题.

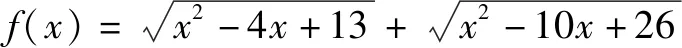
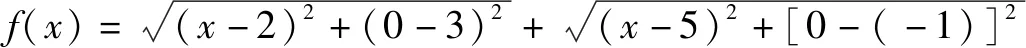
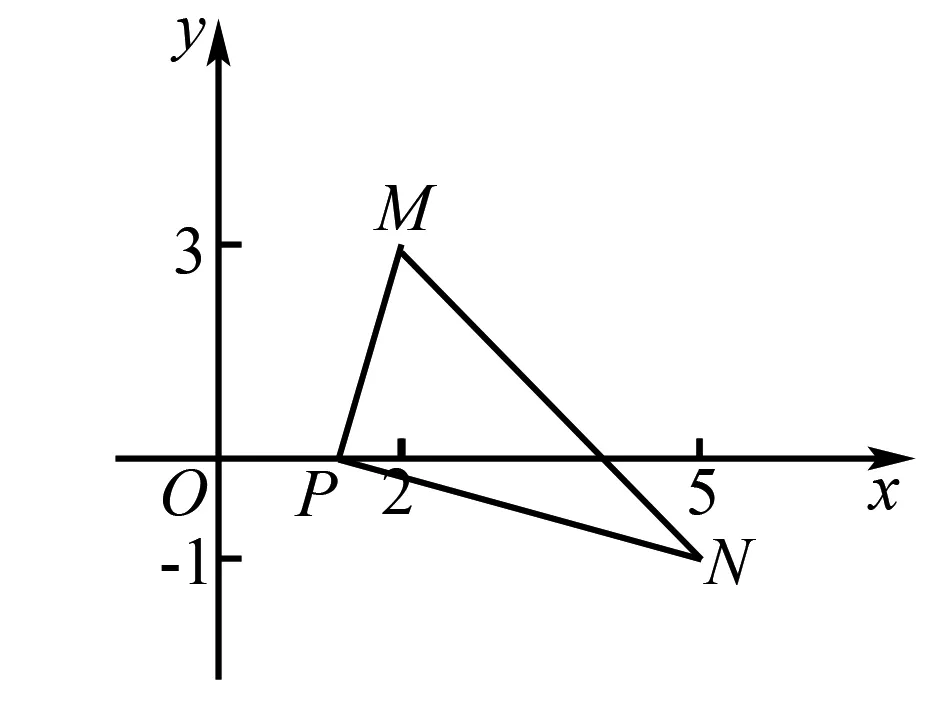
图1

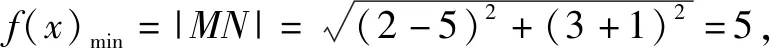
构造法在实际利用的过程中具有非常多的特点与优势，将其应在高中数学解题过程之中的重点在于构造这一过程.高中数学的解题难度相对较高，学生只有拥有良好的数学思维和解题能力的基础上，借助更加灵活有效的方式解决数学问题，才能够使其发挥出更好地效果.学生在利用构造法解决实际问题的过程中，也能够进一步提升自身的能力，进而获得更好的发展.