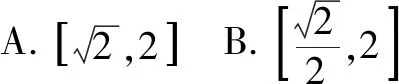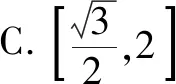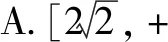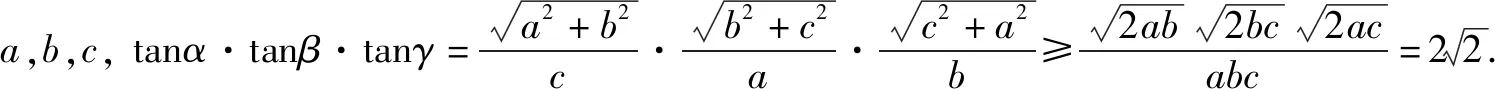谈选择题的解题策略
2021-10-21刘大鹏
刘大鹏
(辽宁省黑山县第一高级中学 121400)
一、构造函数法
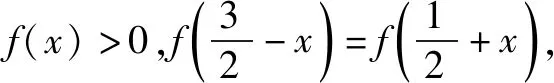
A.a>b>1 B.b>a>1 C.b<1 当x∈(-∞,1)时,g′(x)>0,g(x)单调递增,又因为g(x)图像关于直线x=1轴对称,所以g(x)在(1,+∞)上单调递减,所以选B. 文[2]解答有误,本文加以修正. AB2=AC2+BC2-2AC·BCcosC=4所以选A. 有些题目根据题意画出图像,利用图像的直观性,能很快找到正确选项. 例4 (第5届中学生智能通讯赛)设-1 C. 0.5 有些题目,我们可以采用特殊图形,特殊值,特殊函数,特殊数列,特殊点等特殊化策略,往往能事半功倍,出奇制胜. A.1 B. 2 C. 3 D.4 A.0 B. 2 C.3 D.4 例6 现要给五棱锥P-A1A2A3A4A5的6个面涂上颜色,要求相邻的面不能同色,可供选择的颜色共有5种,则不同的涂色方法种数共有( ). A.1200 B.1440 C 2880 D.720 解记给n棱锥涂色的方法种数为an,则a3=5×4×3×2=120,记ΔPAiAi+1为面i,(A6即A1)当n>3时,考虑an的递推关系,从涂底面开始有5种方法,面1与底面不同,有4种涂法;面2与底面、面1都不同,有3种涂法,同理,面3,…,面n-1都有3种方法,最后到面n,如果只考虑面n与底面、面n-1不同色,仍有3种方法,相乘得5×4×3n-1种涂法. 上面的计算中含有两类情况,一类是面n与面1颜色不同,这符合题意,有an种涂法,另一类是面n与面1颜色相同,此时将这两个面合并看做一个面,有an-1种涂法,即an+an-1=5×4×3n-1,所以a4+a3=5×4×33=540,a4=420,a5+a4=5×4×34=1620,a5=1200. A.4 B.2 C. 1 D.0.5 评注解有关焦半径或焦点弦的问题往往用极坐标方程更方便. 例8 若对x∈(-∞,-1]时,不等式(m2-m)4x-2x-1<0恒成立,则实数m的取值范围是( ). A.(-2,3) B.(-3,3) C.(-2,2) D.(-3,4) 例9 sin218°+sin254°的值为( ). 评注本题也可以直接计算求值,但用到很多公式,不如放缩法便捷,以上两个题目都很有区分度. 例10f(θ)=|cosθ|+|cos2θ|的值域(θ∈R)为( ). 解法1,如图3,设x=|cosθ|,y=|cos2θ|,所以y=|2x2-1|,(0≤x≤1,0≤y≤1).其图像记为曲线C,问题转化为直线x+y=b与曲线C有公共点时,纵截距b的取值范围.选B. 十一、补形法 例11 (第5届中学生智能通讯赛)已知三棱锥V-ABC的三条侧棱两两垂直,P为底面三角形ABC内任意一点,记∠PVA=α,∠PVB=β,∠PVC=γ,则tanα·tanβ·tanγ的取值范围是( ). 解选择题还有一些方法,比如直接法,排除法,极限法,验证法,估算法等等恕不一一举例.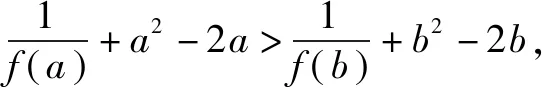
二、复数法
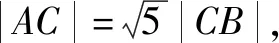
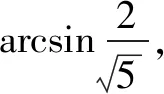
三、定义法

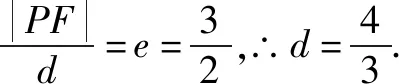

四、数形结合法
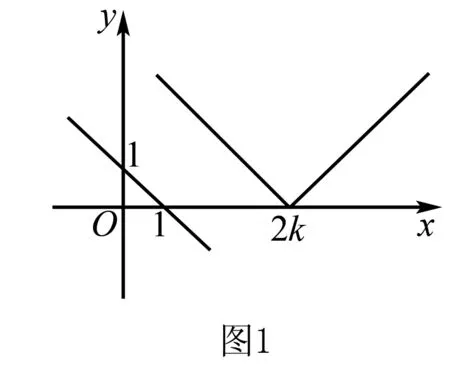

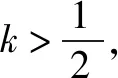
五、特殊化法


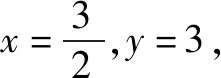

六、递推法
七、极坐标法
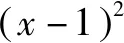

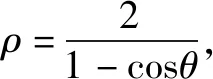
八、分离参数(或参数表达式)法
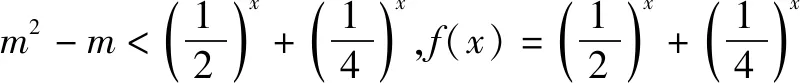
九、放缩法
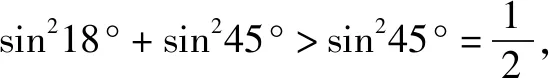
十、换元法