挖掘试题几何背景 优化问题解决策略
——以《解三角形》复习为例
2021-10-21唐明超
唐明超
(云南师范大学信息学院 650500)
解三角形的三条知识主线分别为边、角、面积;主要考查正弦定理、余弦定理与面积公式等核心知识.边的角度多考查中线、角平分线、高线或是其它等分线;角一般涉及互余、互补、相等、公共角;面积既考查单个三角形的面积也考查复合三角形的面积.几何背景以平行四边形、矩形、圆、椭圆为主;设问方式以基本量的直接求解和探究基本量的取值范围两种形式为主.
一、以平行四边形为背景

试题分析本题重点考查三角形的边角关系,属于有一条公共边且公共边为中线的复合三角形问题,其几何背景是平行四边形.处理此类问题的方法较多,思考角度不同可以得出不同的解题方法.

思路2 (坐标法)建立平面直角坐标系,以点C为坐标原点,CB所在直线为x轴,垂直于CB的直线为y轴,求出对应点的坐标后可由坐标运算得出答案.


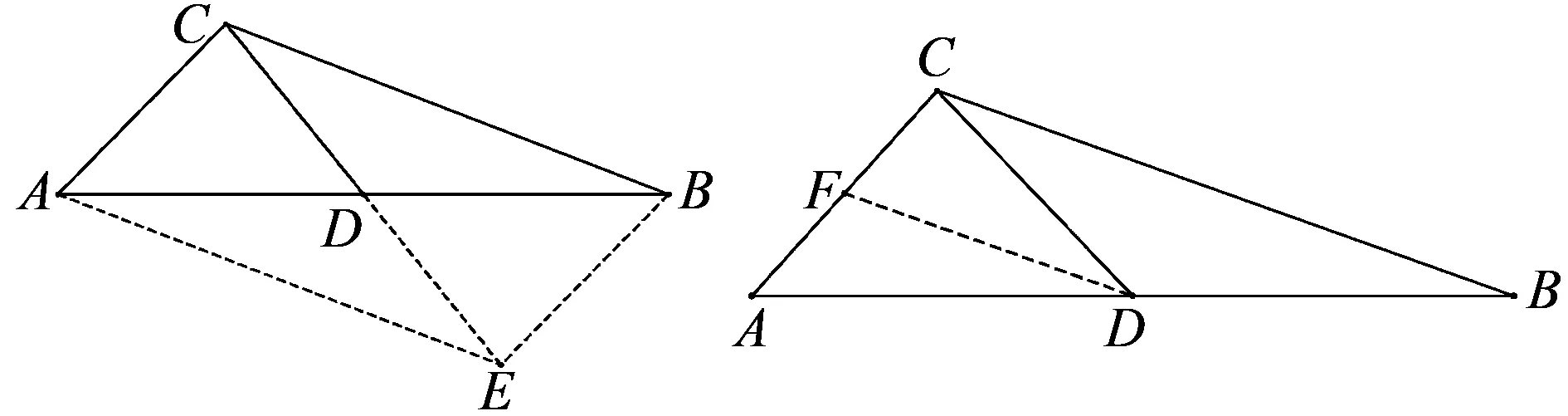
图1 图2



评注该题的求解关键是能挖掘出问题背后所隐藏的平行四边形这一重要几何背景并能充分利用平行四边形的基本性质解决问题.从以上求解思路中可以看出边角关系的合理互化是该类问题解决的基础,但是如果只是单一地追求代数运算必然会出现类似于思路1所呈现的需要在不同的三角形中多次运用正弦定理或者余弦定理,运算量较大,不适用;而另外几种方法充分利用了几何性质,相对于思路1更加优化,思路清晰、过程简洁,提高解题效率.
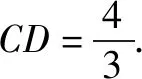

思路2 (坐标法)建立平面直角坐标系,给出对应点的坐标,基于坐标运算得出答案.

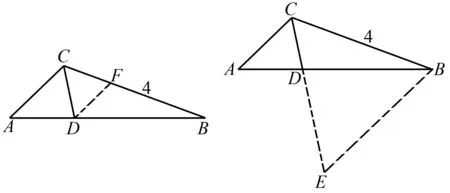
图3 图4

思路5 (三角形面积关系)由S△ACD+S△BCD=S△ACB,得AC=2.
二、以矩形为背景

试题分析可以将例2看作例1的特殊化,思考问题的方向和例1基本相同,解决该题既可以考虑运用正弦定理或余弦定理实现代数运算,也可以重点挖掘问题背后的几何背景并充分利用矩形的几何性质解题.从众多的解法中可以看出充分利用几何背景及其几何性质可以更高效简洁地得出结果.

思路2 (坐标法) 建立相应的坐标系并求出各个点的坐标,最后由坐标运算可得正确结果.


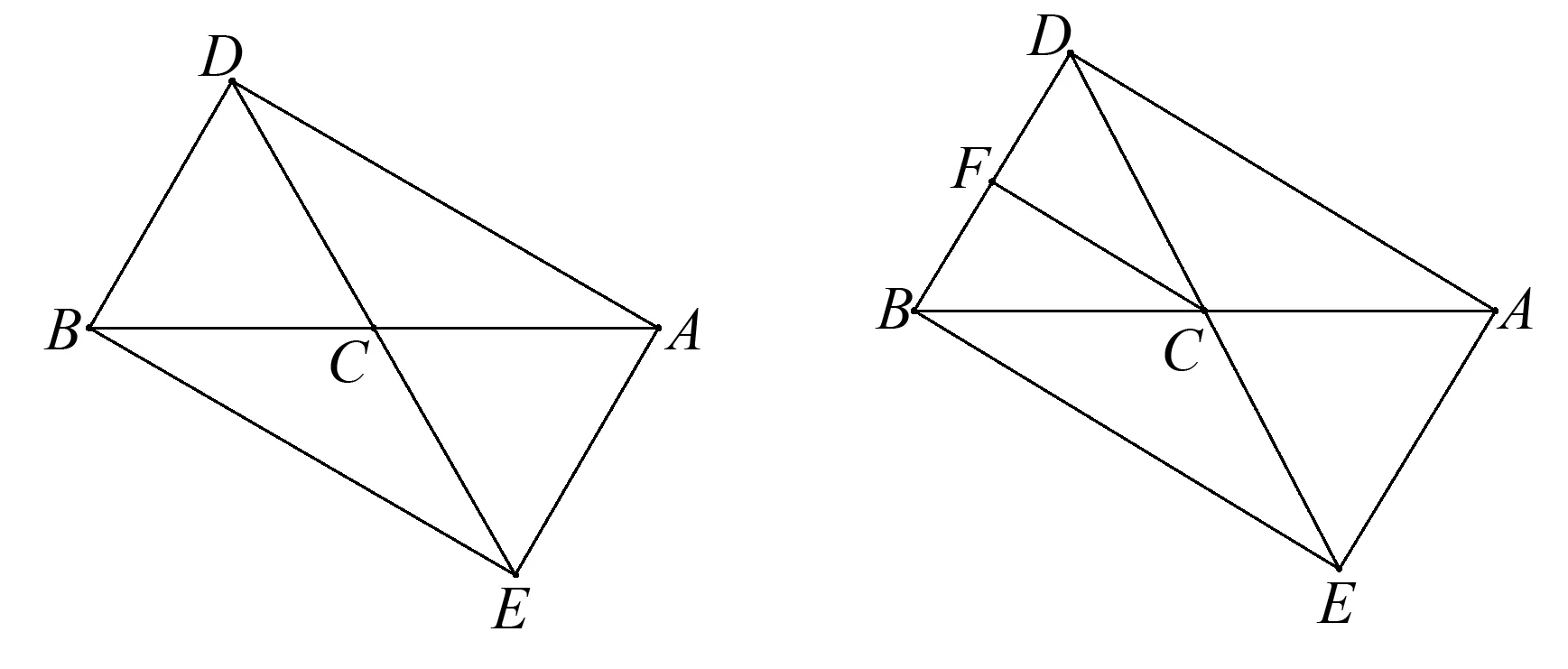
图5 图6

思路6 (三角形相似比+性质)作平行线如图6所示,基于相似比或者中位线性质可得正确答案.
思路7 (三角形面积关系)利用面积关系.由S△ACD+S△BCD=S△ACB且S△ACD=S△BCD.
三、以动态三角形为背景
角度1已知一角及其一边的解三角形问题

(1)求B;
(2)若△ABC为锐角三角形,且c=1,求△ABC面积的取值范围.

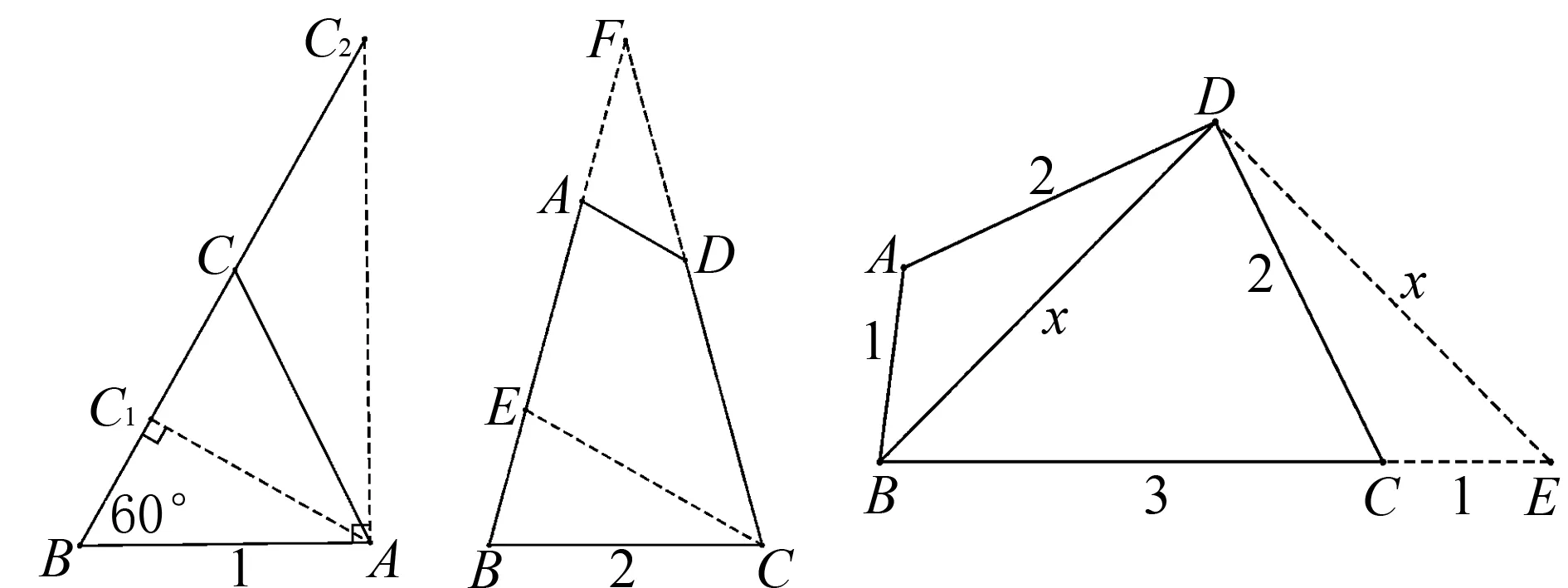
图7 图8 图9
角度2以等腰三角形为背景的割补问题
例4 (2014年新课标Ⅱ卷文17题)四边形ABCD的内角A与C互补,AB=1,BC=3,CD=DA=2.
(1)求∠C和BD;
(2)求四边形ABCD的面积.

四、以圆为背景
角度1已知一边及其对角解三角形
例5 (2013年新课标Ⅱ卷文理17题)△ABC的内角A,B,C的对边分别为a,b,c,已知a=bcosC+csinB.
(1)求B;
(2)若b=2,求△ABC面积的最大值.


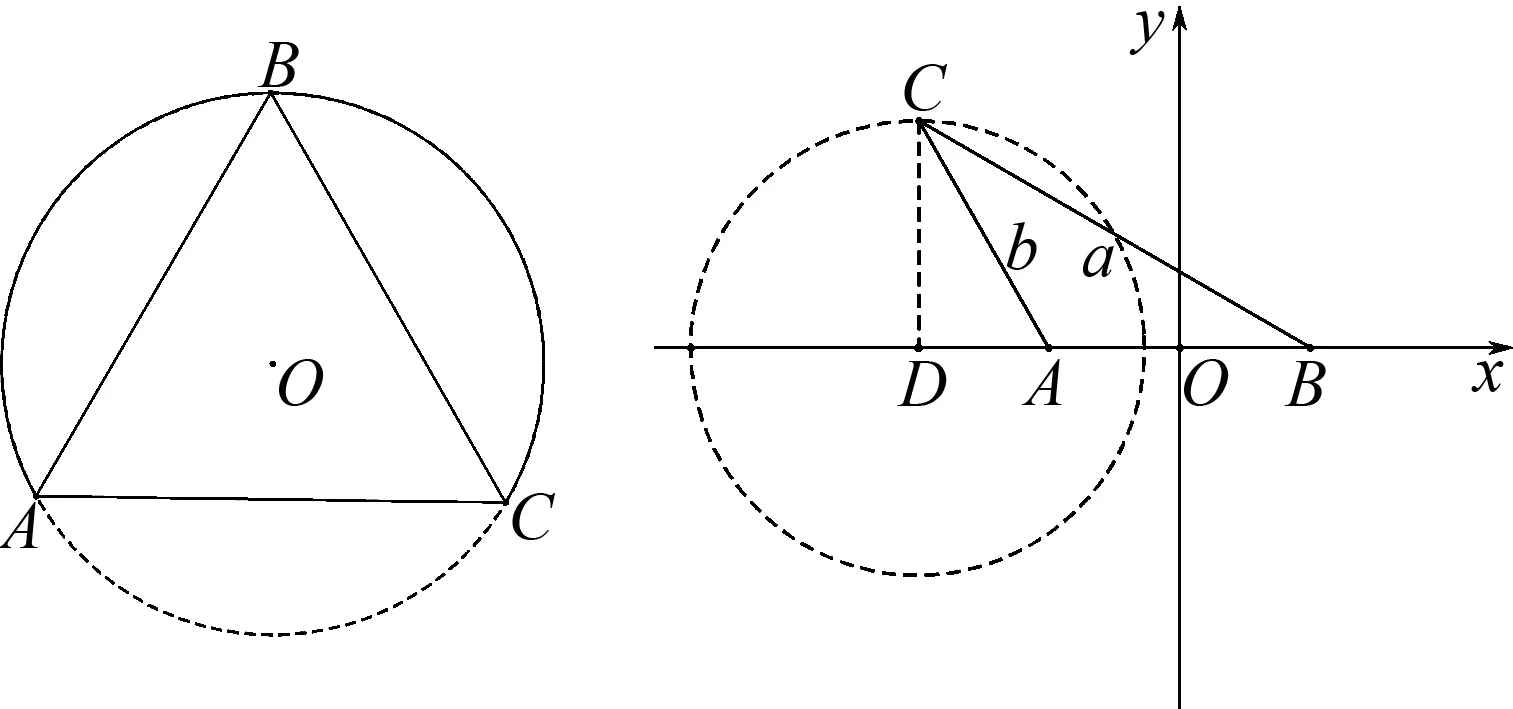
图10 图11
角度2已知一边及另外两边的比值解三角形
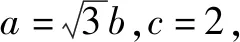
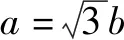
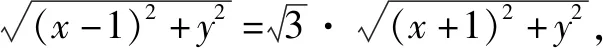
角度3以四边形外接圆为背景的解三角形问题

(1)求DC;

试题分析试题呈现的是有一条公共边的两个三角形复合而成的四边形问题,本质还是解三角形,灵活用好正弦定理与余弦定理可以完成对该题的解答,这也是解三角形的常规思路和一般方法.但是要能顺利解决问题往往需要通过复杂的推理与运算过程,而且在运算的过程中容易出现错误.
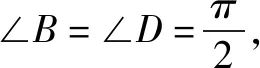
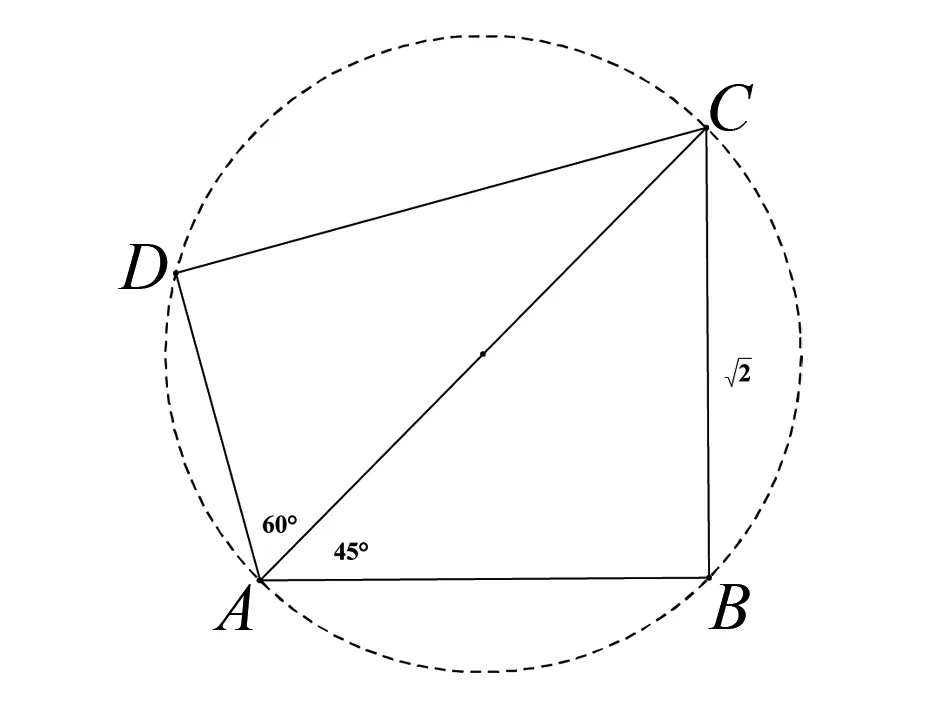
图12
