一道常见不等式题的“变脸记”

龚才权

(江苏省靖江高级中学 214500)

不等式求最值题是高中数学的一个难点，本文尝试从一道常见的不等式求最值题入手，实施一系列的“变脸术”，从而生成一系列的不等式求最值题，以此归纳小结不等式求最值题的解法.

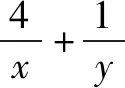
对“题根”实施“变脸术”，令x=m+2，y=2n+1，得到题1.

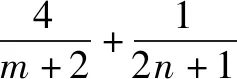
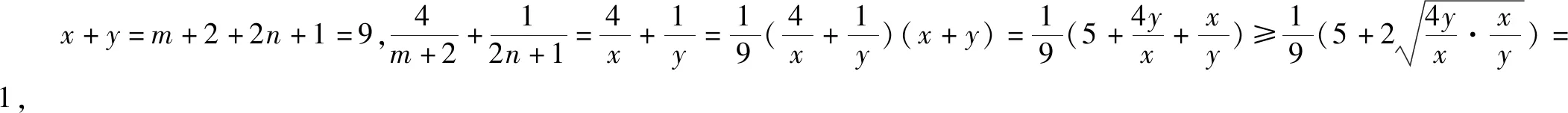
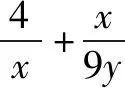
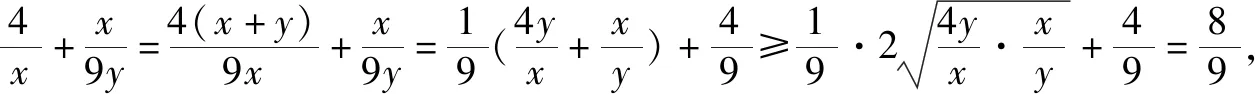
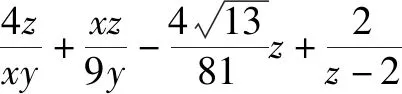
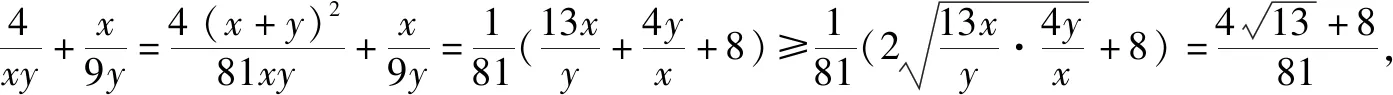
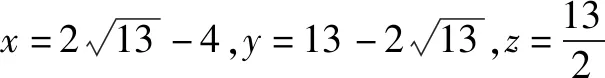
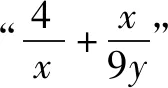
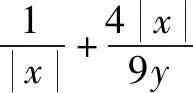
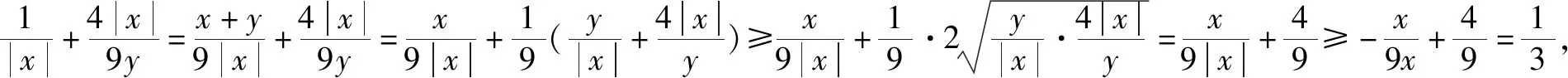
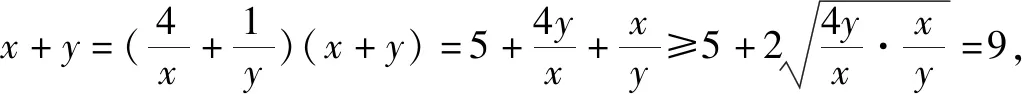
题7 若x>0，y>0，且x+4y-xy=0，求x+y的最小值.

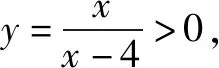
对题7实施“变脸术”，将“x+4y-xy=0”改写为“x+4y-xy+5=0”，得到题8.

题8 若x>0，y>0，且x+4y-xy+5=0，求x+y的最小值.

解令t=x+y，得x=t-y，代入x+4y-xy+5=0中，得y2+(3-t)y+t+5=0，由判别式Δ=(3-t)2-4(t+5)=t2-10t-11≥0，解得t≥11或t≤-1，因为x>0，y>0，所以t≥11，即x+y的最小值为11，此时x=7，y=4.

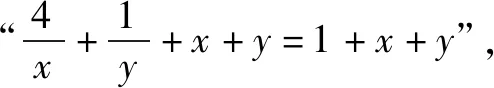
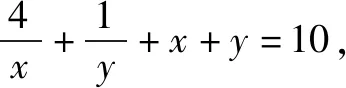
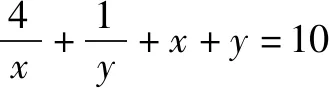
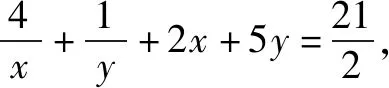
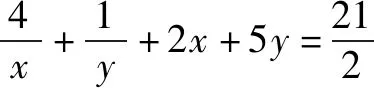
学生总有解不完的题！总有做不完的试卷！新一轮数学课改的目标就是要把学生从题海战术中解放出来.怎样解放？就是以数学高考为指挥棒，让数学高考能真正考查出学生的数学思维能力.数学高考试题以能力立意，学生只有数学思维能力强，才能考得好！不是多刷刷题就能考得好！所以，现在题海战术要不得.题海无涯，回头是岸！岸在哪里？岸在数学教材中！岸在平时数学学习一点一滴的思考中！数学教材中的每个概念，每个定理，甚至是每道例题，每道习题都能成为我们思考的源头.我们要不断地去探究挖掘，才能真正地提高我们的数学思维能力.问渠哪得清如许？为有源头活水来.从源头出发，不断地延伸，不断地拓宽，变成小溪，变成河流，最后必将汇聚成我们数学的汪洋大海！