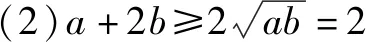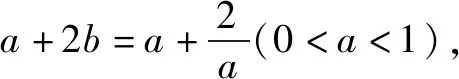解不等式题时要注意等号成立的条件

张岭芝

(江苏省无锡市青山高级中学 214036)

常量与变量之间的等与不等关系问题是数学问题的一类核心问题，由此展现出丰富的数学内涵.把不等号“>”，“<”与“=”天然有机相结合得到“≥”和“≤”，这两个优美的符号完美的诠释了相等与不等和谐共处，不等之中蕴含着相等.

数学问题在一定程度上就是解决等与不等关系，在具体的情境中，往往需要从丰富的相等与不等的条件关系中挖掘相等与不等的结果.

例1已知a>0,b>0且a+b=1求：

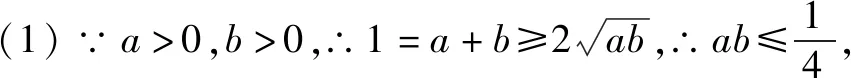
沿用上面的解法我们得到：

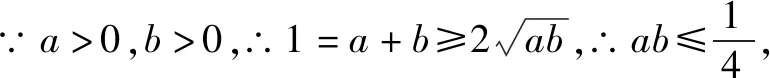
(2)的正确解法：∵a+b=1,

当我们在多次运用基本不等式时,尤其是在运用不等式基本性质进行不等式运算时需要特别注意其中等号成立的条件. 只有当你使用的多个不等式同时成立时最后的相等关系才能取得，如果出现两个或两个以上不等式不能“和谐共处”时最后的相等是无法取得的.因此在解题后多作反思，仔细推敲，别忽视不等式中等号成立的条件！

例2设f(x)=|lgx|，0

(1)2a+b的取值范围；

(2)a+2b的取值范围.

图1

此种类型的问题转化为求一元函数在某区间内上的范围比较可靠，如果是应用基本不等式解题要特别小心，一定要注意挖掘题目中的隐含条件以检验不等式中等号成立的条件是否具备.

例3 函数f(x)=-x3+ax2，若函数y=f(x)的图像上任意不同的两点的连线的斜率都小于2，求实数a取值范围.

上述两种解法孰对孰错？

从数学美的角度来看，“等”体现出数学的均衡与有序之美， “不等”则展现出数学的混浊与奇异之美.从哲学的角度来看，等是相对的，不等才是绝对的，不等之中包含等，等是不等的特殊形态.我们就是要在不等之中寻找相等，在相等之中寻找不等.