传递函数辨识(22): 线性回归系统的递阶迭代参数估计
2021-10-21刘喜梅
丁 锋, 刘喜梅
(1. 江南大学 物联网工程学院, 江苏 无锡 214122; 2. 青岛科技大学 自动化与电子工程学院, 山东 青岛 266061)
迭代辨识方法包括基本的梯度迭代辨识方法、最小二乘迭代辨识方法、牛顿迭代辨识方法等,所以结合递阶辨识原理,派生出递阶梯度迭代辨识方法、递阶最小二乘迭代辨识方法、递阶牛顿迭代辨识方法等。将递阶辨识原理与辅助模型辨识思想相结合,诞生出的迭代辨识方法包括辅助模型递阶梯度迭代辨识方法、辅助模型递阶最小二乘迭代辨识方法、辅助模型递阶牛顿迭代辨识方法等。
将递阶辨识原理与多新息辨识理论相结合,诞生出的迭代辨识方法包括递阶多新息梯度迭代辨识方法、递阶多新息最小二乘迭代辨识方法、递阶多新息牛顿迭代辨识方法等。将递阶辨识原理与辅助模型辨识思想、多新息辨识理论相结合,诞生出的迭代辨识方法包括辅助模型递阶多新息梯度迭代辨识方法、辅助模型递阶多新息最小二乘迭代辨识方法、辅助模型递阶多新息牛顿迭代辨识方法。
在一些系统辨识学术专著[1-6]和连载论文[7-16]中,先后介绍了动态系统和信号模型的参数估计方法。最近在“大系统的递阶辨识”论文[17]基础上,结合梯度搜索和最小二乘搜索原理,连载论文[16]研究线性回归系统的递阶递推辨识方法和递阶递推多新息辨识方法等。进一步,本工作利用迭代搜索技术[5],研究线性回归系统的递阶(多新息)梯度迭代辨识方法和递阶(多新息)最小二乘迭代辨识方法。提出的递阶迭代辨识方法可以推广用于其他线性和非线性随机系统,以及信号模型的参数辨识[18-29]。
1 线性回归系统的递阶辨识模型
《系统辨识——迭代搜索原理与辨识方法》[5]详细介绍了线性回归系统的梯度迭代辨识方法和多新息梯度迭代辨识方法。这里应用递阶辨识原理于线性回归系统,研究基于分解的递阶梯度迭代辨识方法和递阶多新息梯度迭代辨识方法。
考虑下列线性回归系统,
y(t)=φT(t)ϑ+v(t),
(1)
其中y(t)∈是系统输出变量,v(t)∈是零均值随机白噪声,ϑ∈n为待辨识的参数向量,φ(t)∈n是由时刻t以前的输出y(t)和时刻t及以前的输入u(t)等变量构成的回归信息向量。假设维数n已知。不特别申明,设t≤0时,各变量的初值为零,这里意味着y(t)=0,φ(t)=0,v(t)=0。
将参数向量ϑ分解为N个维数为ni的子参数向量(sub-parameter vector)ϑi,将信息向量φ(t)分解为N个维数为ni的子信息向量(sub-information vector)φi(t)如下:

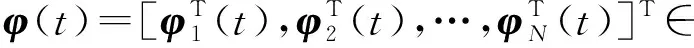
ϑi∈ni,φi(t)∈ni,n1+n2+…+nN=n。
于是,可以把系统(1)分解为N个虚拟子系统(fictitious subsystem),即递阶辨识模型(hierarchical identification model,H-ID模型):
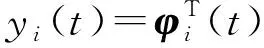
(2)

(3)
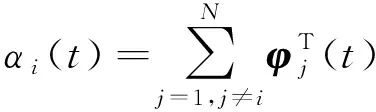
(4)
yi(t)∈是虚拟子系统的输出,αi(t)∈称为各子系统间的关联项(associate item),它是通过参数ϑj(j≠i)耦合的。
迭代辨识算法通常采用批数据估计系统参数。这里辨识的目的是利用观测信息{y(t),φ(t)},推导估计线性回归系统(1)未知参数向量ϑ的递阶梯度迭代辨识方法和递阶多新息梯度迭代辨识方法。
2 递阶梯度迭代辨识方法
2.1 递阶梯度迭代辨识算法


定义堆积输出向量Y(L)和堆积信息矩阵Φ(L),以及虚拟堆积输出向量Yi(L)和堆积子信息矩阵Φi(L)如下:

(5)

(6)
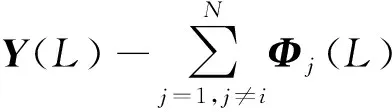
(7)

Φ(L)=
[Φ1(L),Φ2(L),…,ΦN(L)]∈L×n。
(8)
则准则函数J1i(ϑi)可以等价表示为

令k=1,2,3,…为迭代变量,μi>0是迭代步长(收敛因子)。使用负梯度搜索,极小化J1i(ϑi),得到梯度迭代关系:
(9)

(10)
由于特征值计算很复杂,故收敛因子也可简单取为
(11)
注意到虚拟子系统的堆积输出向量Yi(L)是未知的,将式(7)代入式(9)得到

(12)
式(10)~(12),(5)~(6)和(8)构成了估计线性回归系统(1)参数向量ϑ的递阶梯度迭代算法(hierarchical gradient-based iterative algorithm,HGI算法):

(13)
(14)
或
μi≤2‖Φi(L)‖-2,
(15)
Y(L)=[y(1),y(2),…,y(L)]T,
(16)
Φ(L)=[φ(1),φ(2),…,φ(L)]T,
(17)
Φ(L)=[Φ1(L),Φ2(L),…,ΦN(L)],
(18)
(19)
(20)

表1 递阶梯度迭代(HGI)算法的计算量Table 1 Computational efficiency of the HGI algorithm

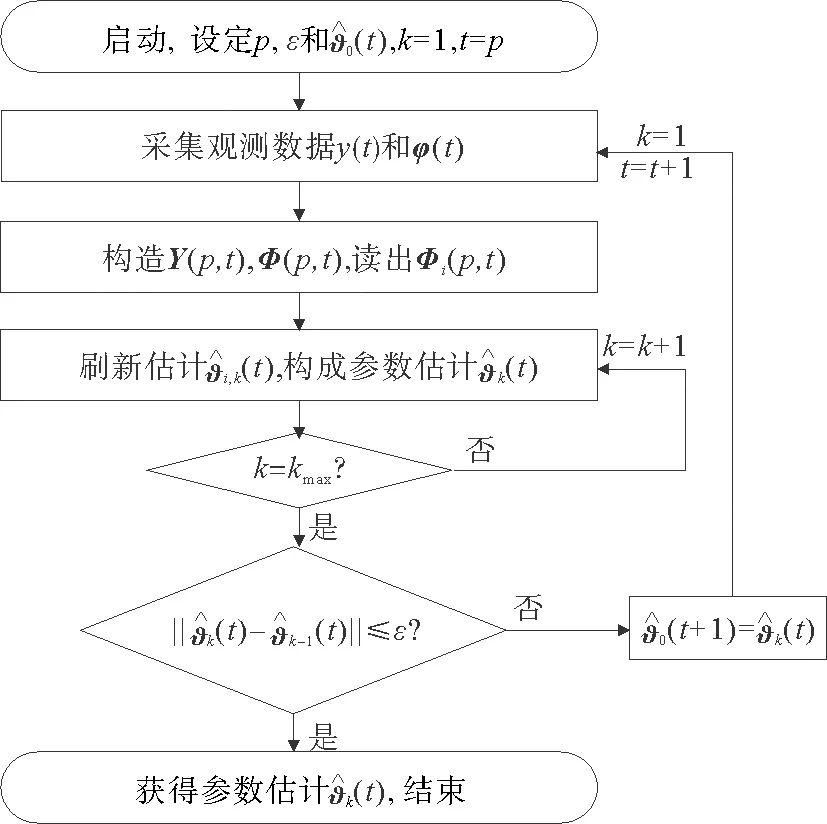
图1 递阶梯度迭代(HGI)算法的计算流程Fig.1 Flowchart of the HGI algorithm

2)采集观测数据y(t)和φ(t),t=1,2,…,L。用式(16)构造堆积输出向量Y(L),用式(17)构造堆积信息矩阵Φ(L)。
3)根据式(18),从堆积信息矩阵Φ(L)中读出堆积子信息矩阵Φi(L),根据式(14)或(15)确定尽量大的步长μi,i=1,2,…,N。

注1算法的参数估计精度依赖于数据长度L,因此数据长度应该足够大。取收敛因子μi=2‖Φi(L)‖-2,在消除中间变量Y(L),Φ(L)和Φi(L)后,HGI辨识算法(13)~(20)可等价表示为
(21)
(22)
(23)
HGI辨识算法(13)~(20)可以派生出许多算法,如修正递阶梯度迭代(M-HGI)算法、加权递阶梯度迭代(W-HGI)算法、遗忘因子递阶梯度迭代(FF-HGI)算法、加权修正递阶梯度迭代(W-M-HGI)算法、遗忘因子修正递阶梯度迭代(FF-M-HGI)算法、加权遗忘因子修正递阶梯度迭代(W-FF-M-HGI)算法等。下面简单介绍其中两个辨识算法。
2.2 加权递阶梯度迭代算法
基于HGI辨识算法(13)~(20),在式(16)~(17)中引入加权因子wt≥0,t=1,2,…,L,就得到估计线性回归系统(1)参数向量ϑ的加权递阶梯度迭代算法(weighted HGI algorithm,W-HGI算法):
(24)
(25)
或
μi≤2‖Φi(L)‖-2,
(26)
Y(L)=[w1y(1),w2y(2),…,wLy(L)]T,
(27)
Φ(L)=[w1φ(1),w2φ(2),…,wLφ(L)]T,
(28)
Φ(L)=[Φ1(L),Φ2(L),…,ΦN(L)],
(29)
(30)
(31)
2.3 遗忘因子递阶梯度迭代算法
基于HGI辨识算法(13)~(20),在式(16)~(17)中引入遗忘因子0≤λ≤1,就得到估计线性回归系统(1)参数向量ϑ的遗忘因子递阶梯度迭代算法(forgetting factor HGI algorithm,FF-HGI算法):
(32)
(33)
或
μi≤2‖Φi(L)‖-2,
(34)
Y(L)=
[λL-1y(1),λL-2y(2),…,λy(L-1),y(L)]T,
(35)
Φ(L)=
[λL-1φ(1),λL-2φ(2),…,λφ(L-1),φ(L)]T
(36)
Φ(L)=[Φ1(L),Φ2(L),…,ΦN(L)],
(37)
(38)
(39)
3 递阶多新息梯度迭代辨识方法
3.1 递阶多新息梯度迭代辨识算法
多新息辨识算法是使用移动数据窗(moving data window,MDW)里的数据刷新参数估计。移动数据窗是一个动态数据窗(dynamical data window),也称为滑动数据窗,它是随t的增加不断向前移动的。数据窗的长度可以是动态变化的,也可以是不变的。本研究假设数据窗长度是不变的。
设新息长度为p,即移动数据窗长度为p,移动数据窗包含从时刻j=t-p+1到当前时刻j=t的p组数据,数据窗是随t的增加而向前移动的。移动数据窗迭代辨识方法是使用直到当前时刻t的最新p组数据进行迭代计算参数估计,当迭代到一定步数(或参数估计精度没有改进)时,就停止迭代计算,而将数据窗向前移动到下一时刻,引入新的观测数据,同时去掉窗里最旧的数据,窗里保持p组数据,再使用新窗里的数据进行迭代计算参数估计,这样周而复始进行下去[5]。
对于线性回归系统,可以建立移动数据窗迭代辨识算法,即多新息迭代辨识算法,来估计其参数向量。这里研究线性回归系统的递阶多新息梯度迭代辨识方法。
长度为p的数据窗随t的增加而向前移动,就称为移动数据窗。它包含了从时刻j=t-p+1到j=t的p组数据。设t为当前时刻。根据辨识模型(2),利用最新的p组数据,定义堆积输出向量Y(p,t)和堆积信息矩阵Φ(p,t),堆积虚拟输出向量Yi(p,t)和堆积子信息矩阵Φi(p,t)如下:
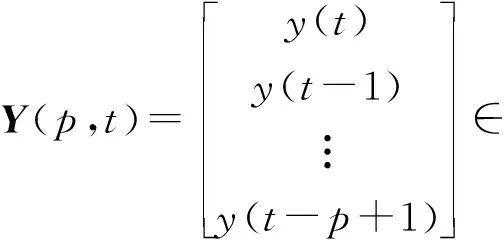
(40)

(41)

(42)

Φ(p,t)=
[Φ1(p,t),Φ2(p,t),…,ΦN(p,t)]∈p×n。
(43)
根据递阶辨识模型(2),定义关于子参数向量ϑi的动态数据窗准则函数:



(44)
故收敛因子μi(t)的一个保守选择是
(45)
由于特征值计算极其复杂,一个简单方式是使用范数,取
(46)
由于虚拟子系统的堆积输出向量Yi(p,t)是未知的,所以将式(42)代入式(44)得到

(47)
式(46)~(47),(40)~(41)和(43)构成了估计线性回归系统(1)参数向量ϑ的递阶多新息梯度迭代算法(hierarchical multi-innovation gradient-based iterative algorithm,HMIGI算法):
(48)
(49)
或
μi(t)≤2‖Φi(p,t)‖-2,
(50)
Y(p,t)=
[y(t),y(t-1),…,y(t-p+1)]T,
(51)
Φ(p,t)=
[φ(t),φ(t-1),…,φ(t-p+1)]T,
(52)
Φ(p,t)=
[Φ1(p,t),Φ2(p,t),…,ΦN(p,t)],
(53)
(54)
(55)
多新息梯度迭代算法又称为移动数据窗梯度迭代算法,是多新息辨识理论在迭代辨识领域中的应用[5]。这里的递阶多新息梯度迭代算法又称为移动数据窗递阶梯度迭代算法(moving data window HGI algorithm,MDW-HGI算法),是递阶辨识原理与多新息迭代辨识相结合的产物,是递阶辨识原理和多新息辨识理论在迭代辨识领域中的应用。
注2因为线性回归系统参数估计误差与数据长度的平方根成反比[3],递阶多新息迭代算法每次计算参数估计时使用的数据长度为p,因此参数估计精度取决于新息长度p,即动态数据窗长度,因此多新息迭代算法中的新息长度p应足够大。
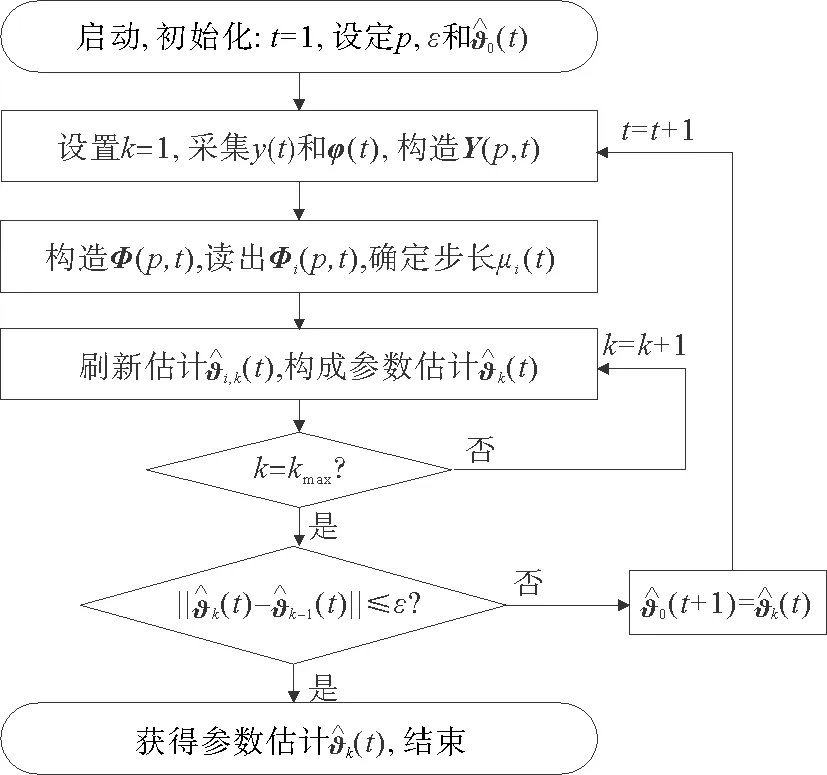
图2 递阶多新息梯度迭代(HMIGI)算法的计算流程Fig.2 Flowchart of the HMIGI algorithm

2)令k=1,采集观测数据y(t)和φ(t)。
3)用式(51)构造堆积输出向量Y(p,t),用式(52)构造堆积信息矩阵Φ(p,t),从式(53)的堆积信息矩阵Φ(p,t)中读出堆积子信息矩阵Φi(p,t),根据式(49)~(50)确定尽量大的步长μi(t),i=1,2,…,N。
5)如果k 当k继续增加,参数估计精度没有明显变化时,就不再增加k,而是增加t,即数据窗向前移动一步,采集新的数据,引入到算法中,同时去掉最旧的数据,再次计算迭代参数估计,直到获得满意的参数估计为止。 根据经验,当参数维数不是很大时,对于梯度迭代算法,kmax取值一般在几百到几千之间;对于最小二乘迭代算法,一般取kmax=5或kmax=6。 注4取收敛因子μi(t)=2‖Φi(p,t)‖-2,在消除中间变量Y(p,t),Φ(p,t)和Φi(p,t)后,HMIGI辨识算法(48)~(55)可等价表示为 (56) (57) (58) HMIGI算法(48)~(55)可以派生出许多算法,如修正递阶多新息梯度迭代(M-HMIGI)算法、加权递阶多新息梯度迭代(W-HMIGI)算法、遗忘因子递阶多新息梯度迭代(FF-HMIGI)算法、加权修正递阶多新息梯度迭代(W-M-HMIGI)算法、遗忘因子修正递阶梯度迭代(FF-M-HMIGI)算法、加权遗忘因子修正递阶多新息梯度迭代(W-FF-M-HMIGI)算法等。下面简单介绍其中两个辨识算法。 基于HMIGI辨识算法(48)~(55),在式(51)~(52)中引入加权因子wt≥0,就得到估计线性回归系统(1)参数向量ϑ的加权递阶多新息梯度迭代算法(weighted HMIGI algorithm,W-HMIGI算法): (59) (60) 或 μi≤2‖Φi(p,t)‖-2, (61) Y(p,t)= [wty(t),wt-1y(t-1),…,wt-p+1y(t-p+1)]T, (62) Φ(p,t)= [wtφ(t),wt-1φ(t-1),…,wt-p+1φ(t-p+1)]T, (63) Φ(p,t)= [Φ1(p,t),Φ2(p,t),…,ΦN(p,t)], (64) (65) (66) 基于HMIGI辨识算法(48)~(55),在式(51)~(52)中引入遗忘因子λ,得到估计线性回归系统(1)参数向量ϑ的遗忘因子递阶多新息梯度迭代算法(forgetting factor HMIGI algorithm,FF-HMIGI算法): (67) (68) 或 μi≤2‖Φi(p,t)‖-2, (69) Y(p,t)= [y(t),λy(t-1),λ2y(t-2),…,λp-1y(t-p+1)]T, (70) Φ(p,t)= [φ(t),λφ(t-1),λ2φ(t-2),…,λp-1φ(t-p+1)]T, (71) Φ(p,t)= [Φ1(p,t),Φ2(p,t),…,ΦN(p,t)], (72) (73) (74) 注5笔者2005年发表在Automatica第2期上的递阶梯度迭代算法[30]和IEEETransactionsonAutomaticControl第3期上的递阶最小二乘迭代算法[31]是比梯度迭代算法和最小二乘迭代算法更高级的算法,是针对多变量系统递阶辨识模型提出的。 注6梯度算法(包括梯度迭代算法)可以用于二次优化问题和非线性优化问题的最优解的搜索,既适合信息向量已知的线性回归系统,又适合信息向量存在未知量的线性回归系统、线性参数系统、双线性参数系统、非线性参数系统辨识的研究。当然梯度迭代算法也适合对线性回归模型进行分解的辨识,如前面讨论的HGI辨识算法和HMIGI辨识算法。 对于信息向量已知的线性回归系统,不存在最小二乘迭代辨识算法,一次完成最小二乘算法就够了,但是对线性回归模型进行分解,就存在最小二乘迭代辨识算法。这里首次讨论线性回归系统的递阶最小二乘迭代算法和递阶多新息最小二乘迭代算法,这是继1999年《自动化学报》第5期上的论文“大系统的递阶辨识”中线性回归系统的递阶最小二乘(递推)算法[17]的又一个新的结果。 考虑下列线性回归系统, y(t)=φT(t)ϑ+v(t), (75) 其中y(t)∈是系统输出变量,v(t)∈是零均值随机白噪声,ϑ∈n待辨识的参数向量,φ(t)∈n是由时刻t以前输出y(t)和时刻t及以前的输入u(t)等变量构成的回归信息向量。假设维数n已知。不特别申明,设t≤0时,各变量的初值为零,这里意味着y(t)=0,φ(t)=0,v(t)=0。 线性回归系统(75)可分解为N个虚拟子系统,即递阶辨识模型: (76) 其中子系统参数向量ϑi和信息向量φi(t)与整个系统的参数向量和信息向量的关系如下: ϑi∈ni,φi(t)∈ni,n1+n2+…+nN=n。 虚拟子系统的输出yi(t)∈定义为 (77) 本节利用观测信息{y(t),φ(t)},推导线性回归系统(75)的递阶最小二乘迭代辨识方法和递阶多新息最小二乘迭代辨识方法。 设L为数据长度。辨识算法的参数估计精度取决于数据长度,因此数据长度应足够大。根据辨识模型(76),定义关于参数向量ϑi的准则函数: 定义堆积输出向量Y(L)和堆积信息矩阵Φ(L),以及虚拟堆积输出向量Yi(L)和堆积子信息矩阵Φi(L)如下: Y(L)=[y(1),y(2),…,y(L)]T∈L, (78) Φ(L)=[φ(1),φ(2),…,φ(L)]T= [Φ1(L),Φ2(L),…,ΦN(L)]∈L×n, (79) Yi(L)=[yi(1),yi(2),…,yi(L)]T= (80) Φi(L)= [φi(1),φi(2),…,φi(L)]∈L×ni。 (81) 则准则函数J3i(ϑi)可以等价表示为 (82) 由于虚拟子系统的堆积输出向量Yi(L)是未知的,所以将式(80)代入式(82)得到 (83) 式(83),(78)和(79)构成了估计线性回归系统(75)参数向量ϑ的递阶最小二乘迭代算法(hierarchical least squares-based iterative algorithm,HLSI算法): (84) Y(L)=[y(1),y(2),…,y(L)]T, (85) Φ(L)=[φ(1),φ(2),…,φ(L)]T, (86) Φ(L)=[Φ1(L),Φ2(L),…,ΦN(L)], (87) (88) (89) 表2 递阶最小二乘迭代(HLSI)算法的计算量Table 2 Computational efficiency of the HLSI algorithm 图3 递阶最小二乘迭代(HLSI)算法的计算流程Fig.3 Flowchart of the HLSI algorithm 2)采集观测数据y(t)和φ(t),t=1,2,…,L。用式(85)构造堆积输出向量Y(L),用式(86)构造堆积信息矩阵Φ(L)。 3)根据式(87),从堆积信息矩阵Φ(L)中读出堆积子信息矩阵Φi(L)。 注7算法的参数估计精度依赖于数据长度L,因此数据长度应该足够大。在消除中间变量Y(L),Φ(L)和Φi(L)后,HLSI辨识算法(84)~(89)可等价表示为 (90) (91) (92) HLSI辨识算法(84)~(89)可以派生出加权递阶最小二乘迭代(W-HLSI)算法、遗忘因子递阶最小二乘迭代(FF-HLSI)算法、加权遗忘因子递阶最小二乘迭代(W-FF-HLSI)算法等。 基于HLSI辨识算法(84)~(89),在式(85)~(86)中引入加权因子wt≥0,t=1,2,…,L,就得到估计线性回归系统(75)参数向量ϑ的加权递阶最小二乘迭代算法(weighted HLSI algorithm,W-HLSI算法): (93) Y(L)=[w1y(1),w2y(2),…,wLy(L)]T, (94) Φ(L)=[w1φ(1),w2φ(2),…,wLφ(L)]T, (95) Φ(L)=[Φ1(L),Φ2(L),…,ΦN(L)], (96) (97) (98) 基于HLSI辨识算法(84)~(89),在式(85)~(86)中引入遗忘因子0≤λ≤1,就得到估计线性回归系统(75)参数向量ϑ的遗忘因子递阶最小二乘迭代算法(forgetting factor HLSI algorithm,FF-HLSI算法): (99) Y(L)= [λL-1y(1),λL-2y(2),…,λy(L-1),y(L)]T, (100) Φ(L)= [λL-1φ(1),λL-2φ(2),…,λφ(L-1),φ(L)]T, (101) Φ(L)=[Φ1(L),Φ2(L),…,ΦN(L)], (102) (103) (104) 设t为当前时刻。根据辨识模型(76),利用最新的p组数据,定义堆积输出向量Y(p,t)和堆积信息矩阵Φ(p,t),堆积虚拟输出向量Yi(p,t)和堆积子信息矩阵Φi(p,t)如下: Y(p,t)= [y(t),y(t-1),…,y(t-p+1)]T∈p, (105) Φ(p,t)=[φ(t),φ(t-1),…,φ(t-p+1)]T= [Φ1(p,t),Φ2(p,t),…,ΦN(p,t)]∈p×n, (106) Yi(p,t)= [yi(t),yi(t-1),…,yi(t-p+1)]T= (107) Φi(p,t)= [φi(t),φi(t-1),…,φi(t-p+1)]T∈p×ni。 (108) 根据辨识模型(76),定义动态数据窗准则函数: (109) 由于虚拟子系统的堆积输出向量Yi(p,t)是未知的,所以将式(107)代入式(109)得到 (110) 式(110),(105)和(106)构成了估计线性回归系统(75)参数向量ϑ的递阶多新息最小二乘迭代算法(hierarchical multi-innovation least squares-based iterative algorithm,HMILSI算法): (111) Y(p,t)= [y(t),y(t-1),…,y(t-p+1)]T, (112) Φ(p,t)= [φ(t),φ(t-1),…,φ(t-p+1)]T, (113) Φ(p,t)= [Φ1(p,t),Φ2(p,t),…,ΦN(p,t)], (114) (115) (116) 多新息最小二乘迭代算法又称为移动数据窗最小二乘迭代算法,是多新息辨识理论在迭代辨识领域中的应用[5]。这里的递阶多新息最小二乘迭代算法又称为移动数据窗递阶最小二乘迭代算法(moving data window HLSI algorithm,MDW-HLSI算法),是递阶辨识原理与多新息迭代辨识相结合的产物,是递阶辨识原理和多新息辨识理论在迭代辨识领域中的应用。 图4 递阶多新息最小二乘迭代(HMILSI)算法的计算流程Fig.4 Flowchart of the HMILSI algorithm 2)采集观测数据y(t)和φ(t)。 3)用式(112)构造堆积输出向量Y(p,t),用式(113)构造堆积信息矩阵Φ(p,t),从式(114)的堆积信息矩阵Φ(p,t)中读出堆积子信息矩阵Φi(p,t),i=1,2,…,N。 6)如果k 注8在消除中间变量Y(p,t),Φ(p,t)和Φi(p,t)后,HMILSI算法(111)~(116)可等价表示为 (117) (118) (119) HMILSI算法(111)~(116)可以派生出加权递阶多新息最小二乘迭代(W-HMILSI)算法、遗忘因子递阶多新息最小二乘迭代(FF-HMILSI)算法、加权遗忘因子递阶多新息最小二乘迭代(W-FF-HMILSI)算法等。 基于HMILSI辨识算法(111)~(116),在式(112)~(113)中引入加权因子wt≥0,就得到估计线性回归系统(75)参数向量ϑ的加权递阶多新息最小二乘迭代算法(weighted HMILSI algorithm,W-HMILSI算法): (120) Y(p,t)= [wty(t),wt-1y(t-1),…,wt-p+1y(t-p+1)]T, (121) Φ(p,t)= [wtφ(t),wt-1φ(t-1),…,wt-p+1φ(t-p+1)]T, (122) Φ(p,t)= [Φ1(p,t),Φ2(p,t),…,ΦN(p,t)], (123) (124) (125) 基于HMILSI辨识算法(111)~(116),在式(112)~(113)中引入遗忘因子λ,得到估计线性回归系统(75)参数向量ϑ的遗忘因子递阶多新息最小二乘迭代算法(forgetting factor HMILSI algorithm,FF-HMILSI算法): (126) Y(p,t)= [y(t),λy(t-1),λ2y(t-2),…,λp-1y(t-p+1)]T, (127) Φ(p,t)= [φ(t),λφ(t-1),λ2φ(t-2),…,λp-1φ(t-p+1)]T, (128) Φ(p,t)= [Φ1(p,t),Φ2(p,t),…,ΦN(p,t)], (129) (130) (131) 利用迭代搜索和递阶辨识原理,基于系统的观测输入输出数据,研究了线性回归系统的递阶迭代辨识方法,包括递阶(多新息)梯度迭代辨识方法、递阶(多新息)最小二乘迭代辨识方法,以及加权和遗忘因子递阶迭代辨识方法等。提出的迭代辨识方法可以推广到有色噪声的多变量随机系统和非线性随机系统中。

3.2 加权递阶多新息梯度迭代算法
3.3 遗忘因子递阶多新息梯度迭代算法
4 递阶最小二乘迭代辨识方法
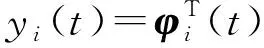

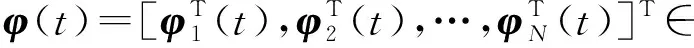

4.1 递阶最小二乘迭代辨识算法









4.2 加权递阶最小二乘迭代辨识算法
4.3 遗忘因子递阶最小二乘迭代算法
5 递阶多新息最小二乘迭代辨识方法
5.1 递阶多新息最小二乘迭代辨识算法











5.2 加权递阶多新息最小二乘迭代算法
5.3 遗忘因子递阶多新息最小二乘迭代算法
6 结 语
