基于马尔科夫链的短车道通行能力建模*
2021-10-21余志许焕挺何兆成
余志,许焕挺,何兆成
中山大学智能工程学院,广东广州 510006
交叉口一直以来都是车辆运行的瓶颈,为了降低瓶颈带来的影响,常使用拓宽车道的方式提高通行能力[1]。这种在交叉口处拓宽形成的车道,因存在一定的长度限制、无法当作独立车道而被称为短车道[2]。拓宽信号交叉口进口道是提高其通行能力的有效方法,但短车道也是影响通行能力的潜在因素,常导致相关车流互相影响,甚至发生短车道排队阻塞,这种阻塞被称为短车道效应[2]。因此,设计手册规定了短车道的最短长度[3-5]以降低短车道排队阻塞发生的概率。
短车道效应的发生是道路、交通、管理条件综合作用的结果,为了探究短车道对交叉口交通运行的影响,Wu[6]指出传统方法和HCM 对于短车道组通行能力的估计存在高估或是低估的情况,并提出了一种基于概率论的短车道通行能力估计方法。研究表明,带有短车道的信号控制交叉口的通行能力与短车道长度、车流比例,以及周期时长有很大关系[7]。Wu[8]考虑交通流的随机性和排队阻塞对短车道的影响,建立了一个理论-经验模型来计算短车道组的通行能力。马万经等[9-10]考虑相邻周期排队作用,建立左转短车道阻塞概率和通行能力解析模型。以往的研究揭示了短车道通行能力是道路几何条件、车流比例、信号控制方案等因素综合作用的结果,在过程中使用了基于概率的修正模型,此类方法考虑了车辆到达及车流互阻塞的随机性,更接近实际情况,成为当前研究该问题的主流方法。
然而,已有工作大多以周期为粒度,独立研究短车道和相邻车道的短车道效应发生概率以及阻塞影响下的通行能力水平,忽略了短车道和相邻车道车辆运动的耦合性以及连续性。由于不同流向的车辆运动在信号交叉口是根据相位进行划分的,这种分流向车辆运动的耦合性和连续性将导致当前相位车辆排队状态一定程度上依赖于上一相位的排队状态,使信号交叉口的阻塞概率和通过量处于动态变化当中。针对上述问题,本文基于概率论和马尔科夫链相关理论,以相位为最小粒度对信号交叉口的短车道组通行能力进行了建模,分析了其在不同交通条件和道路几何条件下的变化。
1 基于马尔科夫链的短车道通行能力计算模型
为不失一般性,本文以滞后的受保护左转相位下直左短车道组进行研究,并且左转的有效绿灯时间长于短车道最大排队清空时间,以限制短车道最大容量。本文模型基于两个假设:1) 车辆到达服从泊松分布;2) 车辆均为标准小汽车。模型的计算流程图如图1所示。
1.1 构建相位状态转移的马尔科夫链
根据相位设置和短车道组车辆运动情况将周期分成三个阶段:排队阶段、直行通行和左转通行,记为T1、T2、T3,如图2 所示。将每阶段结束时刻短车道车辆排队状态视为该阶段状态,状态空间为{B,O,S}。其中,B 表示直行阻塞左转通行,O表示左转阻塞直行通行,S表示不阻塞,各状态如图3所示。
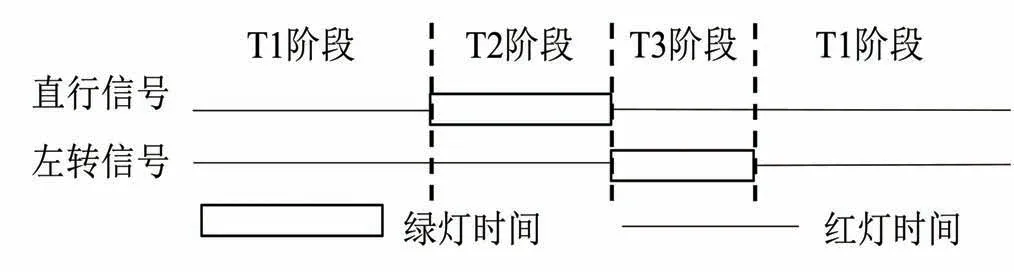
图2 信号控制方案周期划分Fig. 2 Division of signal control scheme

图3 排队状态示意图Fig. 3 The system status of queue in short lanes
考虑到每个相位阶段的车辆排队状态只取决于上一阶段的状态,为
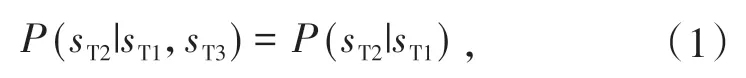
其中P(sTi)表示短车道处于sTi状态的概率,sTi表示Ti阶段的状态,sTi∈{ B,O,S }。
因此,相邻阶段之间状态转移过程可以构建成为一条马尔科夫链。对于本模型的马尔科夫链来说,每经过三个阶段为一次迭代,使用P(k)表示第k次迭代计算时的短车道组相位状态概率矩阵,矩阵每一行元素表示一个阶段不同状态的概率,每一列元素表示一种状态在不同阶段的概率。矩阵元素取值范围为[0,1],且每一行元素满足是满足该约束的随机矩阵。
1.2 剩余容量矩阵
定义剩余容量为短车道容量与短车道范围排队车辆数的差值,根据车道可以分成左转车道剩余容量和直行车道剩余容量。第k次迭代时,短车道组左转车道的剩余容量矩阵为
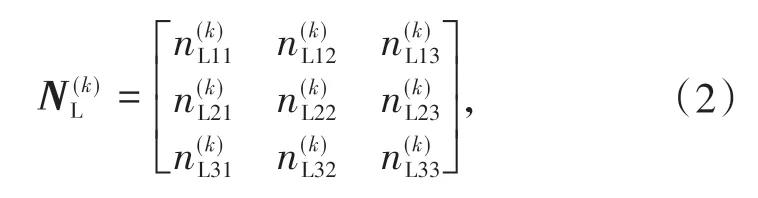
其中为左转车道在第i阶段处于第j状态的剩余容量。类似的,第k次迭代时直行车道的剩余容量矩阵为
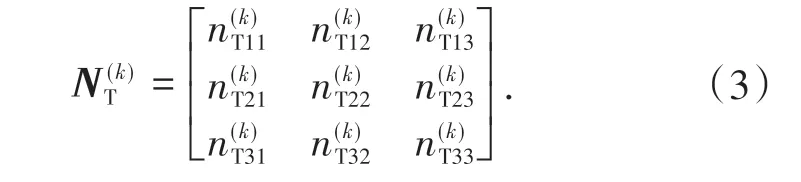
1.2.1 T1 阶段剩余容量计算在T1 阶段时,直行和左转车辆都处于排队状态,如果在该阶段结束的时候,处于S状态,即车辆顺畅通行,则此时短车道剩余容量等于短车道容量N减去平均到达车辆数。到达车辆数服从泊松分布,且达到车辆数小于等于N,所以短车道剩余容量为
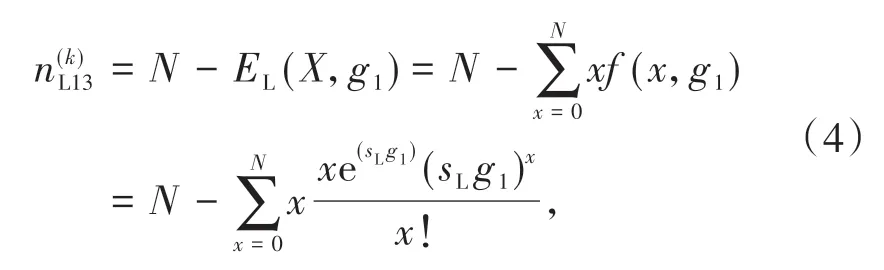
其中EL(X,g1) 表示左转车道到达车辆数期望,g1表示T1 阶段绿灯时间;sL表示左转车辆到达率,由上游车道车辆到达率λ乘上左转车流比例βL得到,即sL=λβL。同理,直行车道剩余容量为
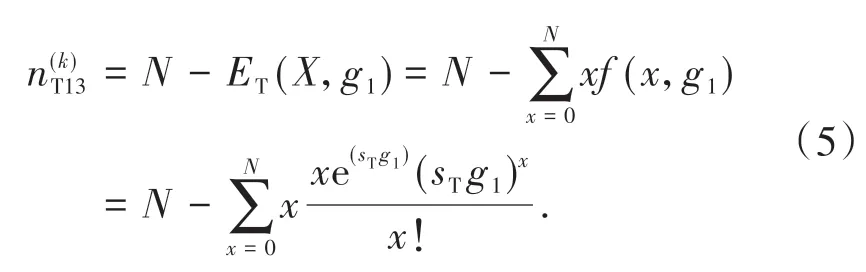
如果T1 阶段结束的时候,处于B 状态,即直行车排队阻塞左转; T1 阶段的B 状态有可能是从T3 阶段的B 状态,也有可能是从T3 阶段的S 状态演变而来,其中T3阶段的B状态和S状态的概率为和。无论什么状态,T1 阶段直行车道的剩余容量=0。对左转车道来说,如果从B 状态演变而来,则T1 剩余容量等于T3 阶段B 状态的剩余容量;若从S 状态演变而来,则T1 剩余容量等于T3 阶段S 状态的剩余容量减去T1 阶段期间在直行阻塞左转前到达的左转车辆数。因此,短车道剩余容量为
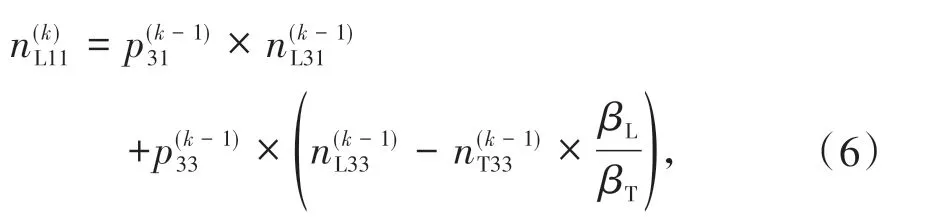
如果T1 阶段结束的时候,处于O 状态,即左转车排队阻塞直行,该状态只能由T3 阶段的S 状态演变而来。此时,左转车道剩余容量直行车道剩余容量受上一阶段状态影响,等于T3阶段直行车道剩余容量减去T1 阶段到达直行车辆数。直行车道剩余容量为
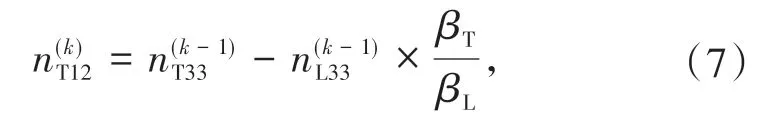
1.2.2 T2 阶段剩余容量计算T2 阶段出现B 状态的概率为0,此时的短车道和直行车道的剩余容量都为N,且
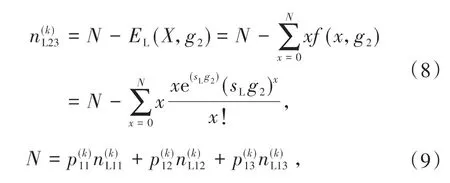
其中g2表示T2阶段的绿灯时间。
1.2.3 T3 阶段剩余容量计算类似T2 阶段,T3阶段出现O 状态的概率为0,阶段结束时的状态为B状态时,直行车道剩余容量,短车道的剩余容量;若T3阶段结束的时候状态为S 时,短车道的剩余容量直行车道剩余容量为
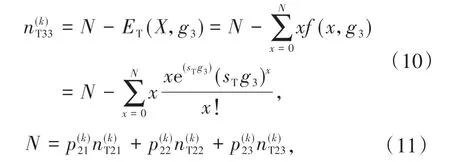
其中g3表示T3阶段的绿灯时间。
1.3 马尔科夫链的转移概率和转移矩阵
第k次迭代过程中,从上阶段到Ti阶段状态转移概率矩阵用表示。矩阵每个要素表示基于上阶段某个状态下本阶段状态的概率,且
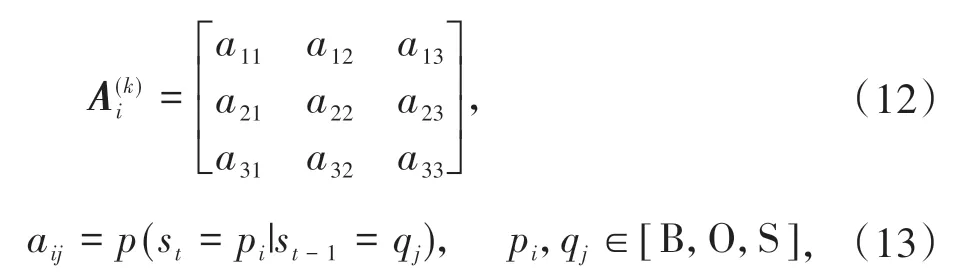
1.3.1 T3 阶段到T1 阶段转移矩阵T1 阶段直行车和左转车均排队,T1 阶段结束时处于B 状态的概率等价于直行车道的到达车辆数先超过其剩余容量的概率,为
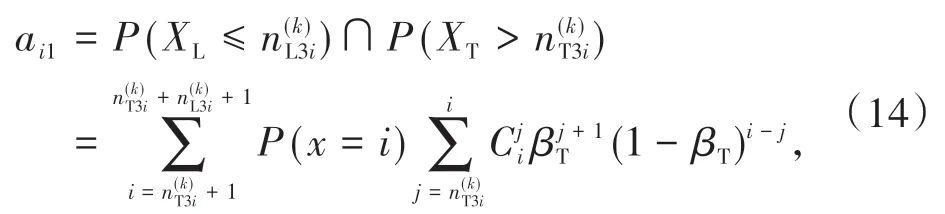
T1阶段结束时处于O状态的概率为
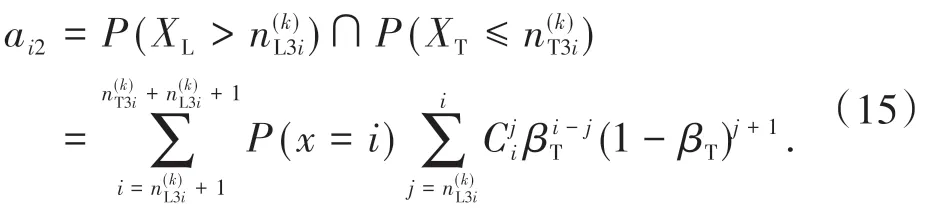
T1阶段结束时,处于S状态的概率为
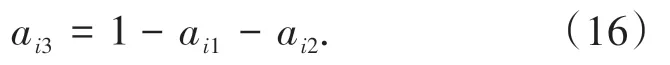
1.3.2 T1 阶段到T2 阶段转移矩阵T2 阶段处于直行车通行和左转车排队相位下,因此T2 阶段结束时处于B状态的概率为0,即ai1=0。
T2 阶段结束时处于O 状态的概率,等价于左转车道到达车辆数超过其剩余容量的概率,为
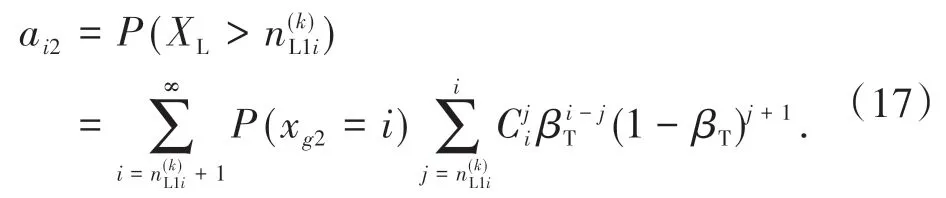
T2阶段结束时处于S状态的概率为
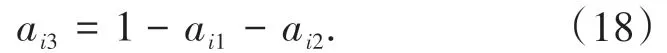
1.3.3 T2 阶段到T3 阶段转移矩阵T3 阶段直行车排队和左转车通行,因此T3 阶段结束时处于O状态的概率为0,即ai2=0.
T3阶段结束时处于O状态的概率为
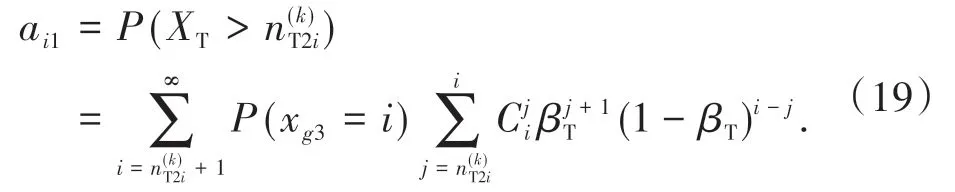
T3阶段结束时处于S状态的概率为
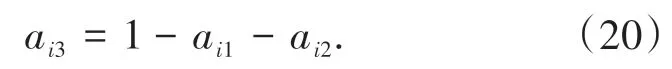
1.4 相位状态概率矩阵的更新
根据上述计算得到的转移概率矩阵进行相位状态概率矩阵的更新,更新公式为
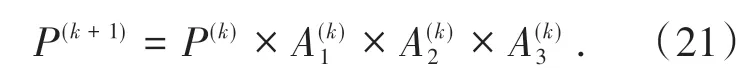
更新停止条件为
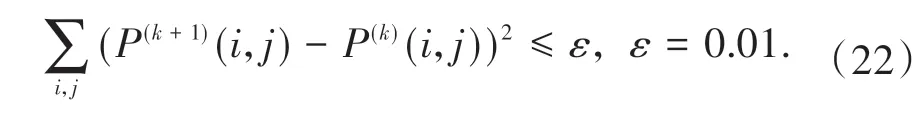
1.5 条件通行能力矩阵的计算
条件通行能力是指考虑上一阶段状态下本阶段处于某状态时的通行能力。对于左转通行能力来说,其通行相位处于T3 阶段,因此其条件通行能力矩阵元素为考虑T2 阶段各状态下的通行能力,为

其中矩阵每一列表示T3 阶段的一种状态,每一行表示T2阶段的一种状态。
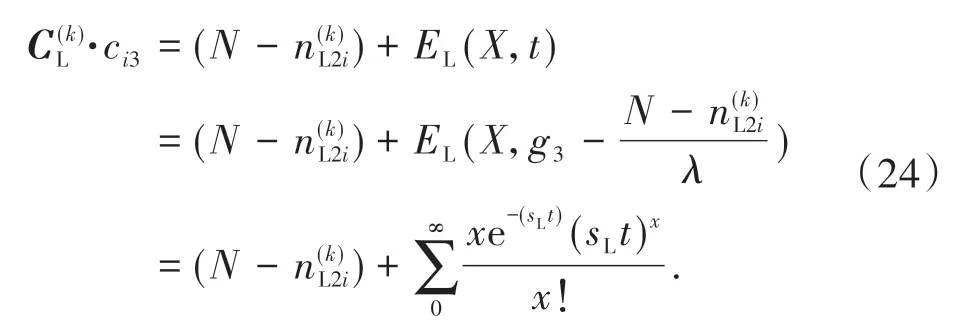
但T3 阶段处于B 状态时,短车道因为被阻塞无法充分利用。此时,通行能力由上阶段结束时短车道排队车辆数和本阶段短车道到达车辆数两部分组成,为
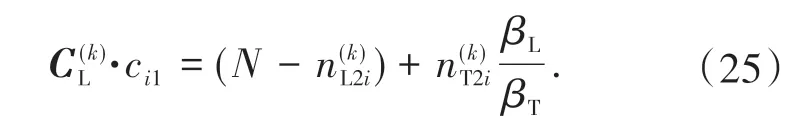
同理,直行车道条件通行能力矩阵为
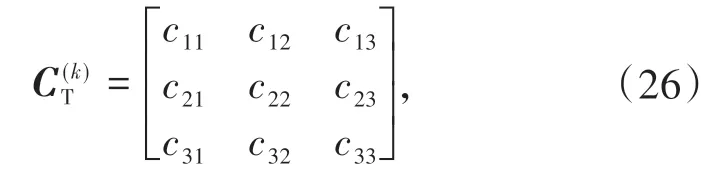
且
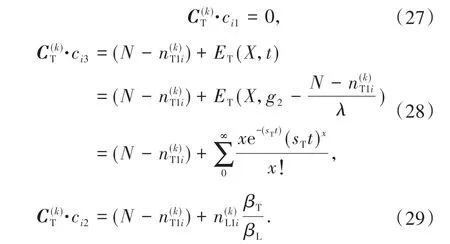
1.6 通行能力计算
根据相位状态概率矩阵和条件通行能力矩阵,可以计算短车道组的通行能力。左转通行能力和直行通行能力分别为
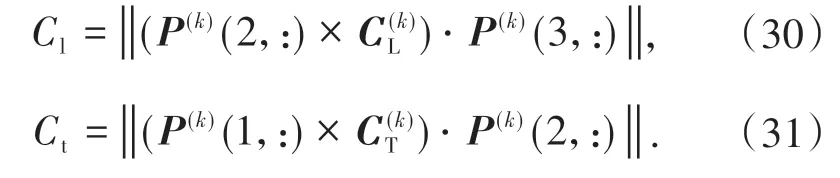
2 模型验证
为了验证模型合理性和准确性,本文使用VISSIM 仿真工具进行场景模拟和仿真。选取广州市猎德大道和花城大道交叉口的东进口作为试验对象。试验前,使用晚高峰交叉口的到达率和通过量对仿真场景进行标定工作。试验场景采取先直行后左转的相位配置方式,信号控制方案的周期为165 s,直行相位的时间为38 s,左转相位时长为22 s。交通流参数配置中车辆饱和流率为0. 6 pcu/s,车辆排队启动时间为2 s。
记本文模型为模型1,设置对照模型进行对比,记对照模型为模型2。对照模型不使用马尔科夫链计算阻塞概率,根据公式(31) 计算直行车道阻塞概率为
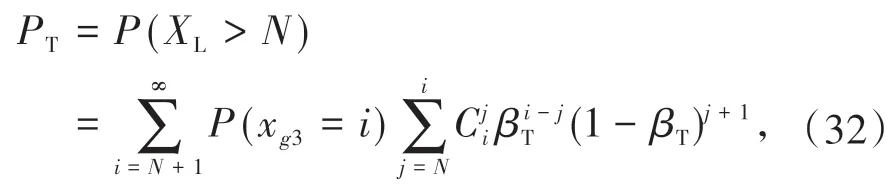
左转车道阻塞概率的计算同理。
2.1 不同交通需求模式下的模型验证
交通需求模式在本研究中体现在短车道车流比例上,因此本节研究车流比例下的通行能力水平。根据短车道实际的几何条件,设置短车道容量为8 pcu,不同车流比例下的通行能力如图4所示。
由图4 (a) 可以看出,模型计算结果在不同需求比例下都高于仿真值,但两者整体趋势相同,且相对误差在10% 以下。经秩和检验可知,在95% 置信水平下模型与仿真结果无显著性差异。从图4 (b) 和(c) 可看出,相较于HCM 计算结果,模型1 和模型2 短车道组的左转通行能力和直行通行能力都与仿真值的变化趋势相同,且数值上更加接近。对模型1 与仿真结果进行秩和检验,结果表明,在95% 置信水平下,模型1的左转和直行通行能力与仿真结果无显著性差异。虽然模型1和模型2整体上误差较为接近,但从左转和直行通行能力的误差上看,明显模型2的误差高于模型1。
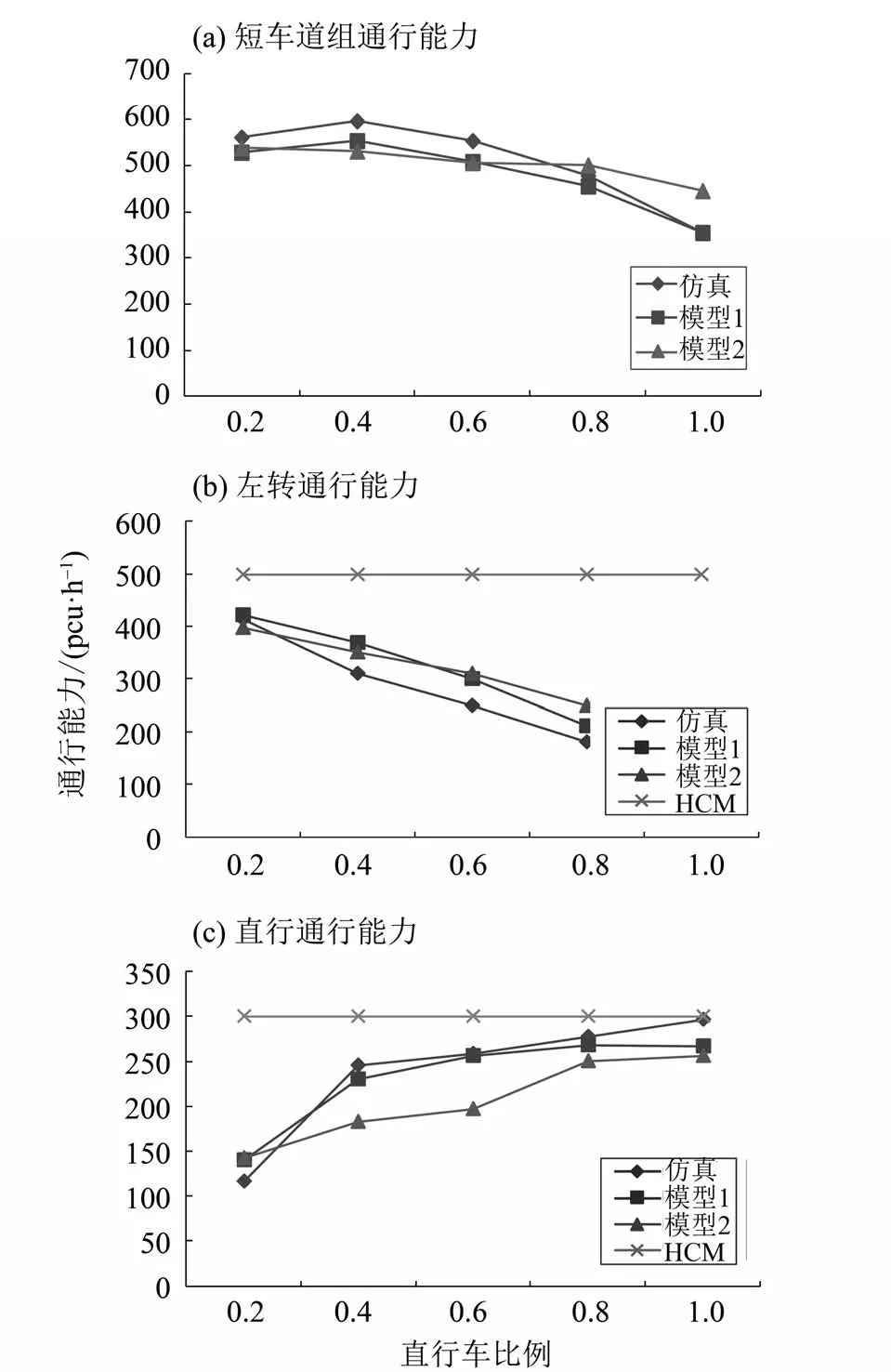
图4 短车道车流比例与通行能力的关系Fig. 4 Relationship between flow ratio and traffic capacity of short lanes
2.2 不同短车道几何条件的模型验证
短车道的几何条件变化体现在短车道容纳的标准小车数。因此,本节根据实测数据,设置直行需求比例为0. 6,通过调整短车道的容量来验证本文模型,不同短车道容量下通行能力如图5所示。
由图5 (a) 可以看出,短车道组通行能力随着短车道车容量的增加而增加,模型与仿真值整体趋势相同,且短车道通行能力模型和仿真值相对误差在10% 以下。经秩和检验可知,在95% 置信水平下模型与仿真结果无显著性差异。从图5(b) 和(c) 可看出,模型1和模型2短车道组的左转通行能力和直行通行能力都与仿真值的变化趋势相同,且均优于HCM 计算结果。对模型1 进行秩和检验,在95% 置信水平下,左转和直行通行能力在模型与仿真结果上都无显著性差异。虽然模型2 在整体上的准确性比模型1 高,但是这种准确性是建立在对直行通行能力的高估和左转通行能力的低估之上。从直行通行能力和左转通行能力上观察,可以发现模型1在两者的准确性都高于模型2。
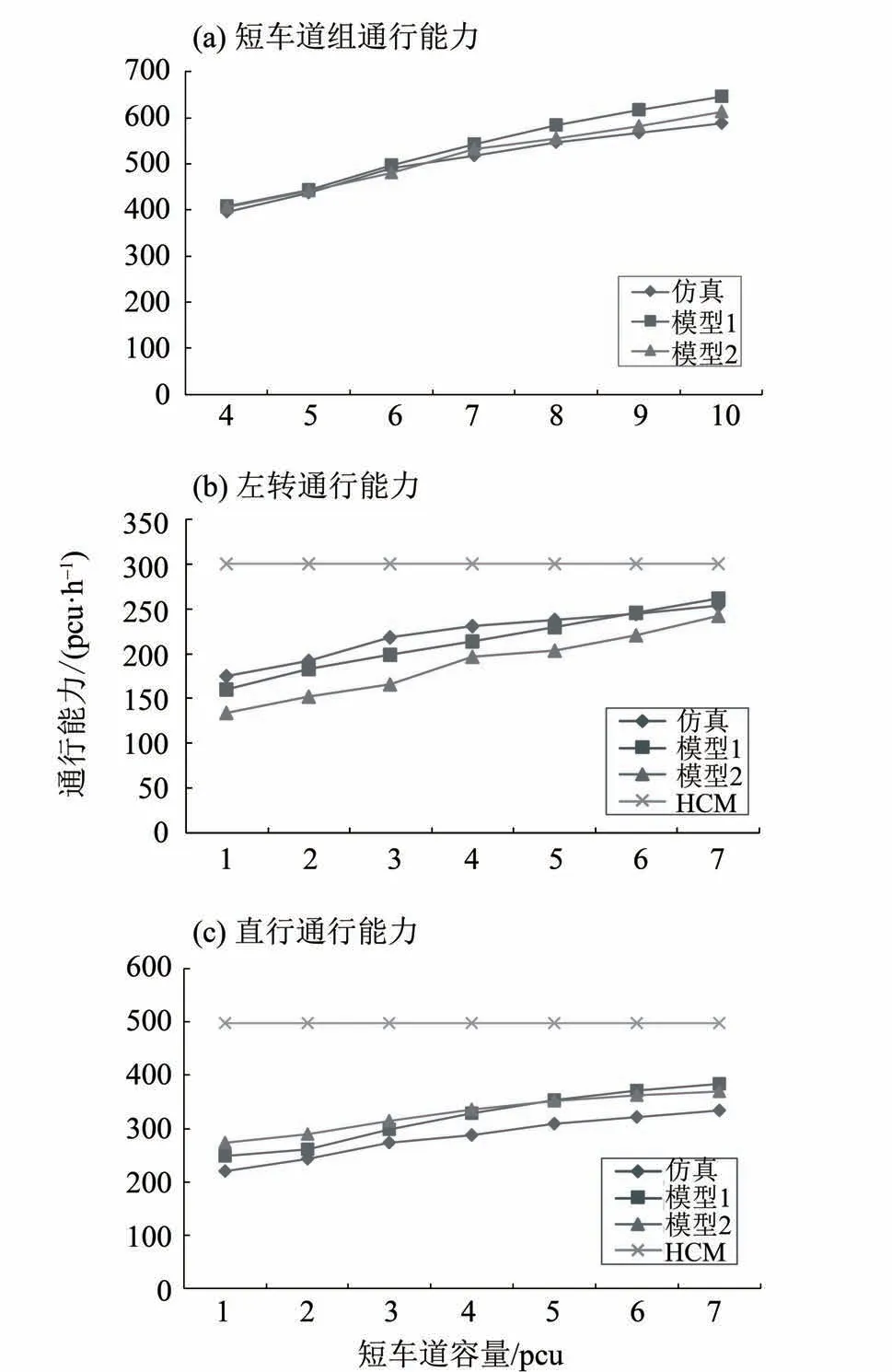
图5 短车道容量与通行能力的关系Fig. 5 Relationship between storage and traffic capacity of short lanes
本节通过将本文模型在不同需求比例和短车道几何条件下与仿真进行对比,得知:基于标定后的仿真运行结果,本模型已有较高的准确性,在整体和部分上均能够反映实际的通行能力水平。同时,通过与不考虑相位状态转移的模型进行对比,发现本文模型能够在直行和左转通行能力上具有更高的拟合效果, 证明了本文方法的有效性。
3 结 论
本文提出了一个基于马尔科夫链的短车道通行能力模型。考虑短车道阻塞效应发生的随机性和动态性,研究不同需求比例和短车道几何条件下的模型准确性和短车道通行能力特点,得到以下结论:
1) 从需求比例和短车道几何条件来看,本文提出的模型能够比较准确地反映短车道组的通行能力,使用马尔科夫链拟合短车道组状态的动态转移过程是可行的。
2) 当前相位的阻塞概率确实受到前一相位状态的影响,考虑相位的状态转移有助于得到更加准确的短车道组通行能力。
3) 在短车道组通行能力计算过程中,车流需求比例比短车道容量对结果影响更大。在实际应用过程中,可以考虑控制交叉口的转向需求,来获得较高的通行能力。
