基于深度神经网络的格子玻尔兹曼算法*
2021-10-21陈辛阳聂滋森蒋子超杨耿超姚清河
陈辛阳,聂滋森,蒋子超,杨耿超,姚清河
中山大学航空航天学院,广东广州 510006
格子玻尔兹曼算法(LBM,Lattice Boltzmann method) 起源自格子气自动机(LGA,lattice gas automaton),是一种新兴的计算流体力学方法,相较于传统计算流体力学(CFD, computational fluid dynamic) 方法,LBM 有易于处理边界条件,适合复杂几何形状,程序结构简单及可并行性高等优点[1]。然而,LBM 存在计算资源消耗大以及对设备配置要求高等缺陷。具体来讲,造成LBM 消耗大量计算资源的原因主要有两点。第一,每一迭代内的计算资源消耗大,针对这一方面的相关研究主要是利用GPU 并行的方法降低计算资源消耗,目前已经形成了较为成熟的相关技术[2];第二,由于LBM 是一个显式算法,为了保障计算的稳定性和精度,计算步长常常设置得较短,而较短的步长将导致迭代次数增多,大幅增加计算资源的消耗[3]。本文将从第二点出发,以单次模型计算代替较多计算步长小的普通LBM 迭代,从而减少计算资源的消耗。
在降低CFD 模型计算复杂度方面研究较多的是降维法(ROM,reduced order methods),比如:Xie 等的一种基于数据驱动的降维法(DDFROM),在构建非封闭ROM 后使用数据驱动模型矫正ROM,提高了模型的精度[4];De Witt 和Lessig 等提出了改进ROM 法,提高计算效率并在小自由度下完成了可靠的流场可视化模拟[5]。ROM 方法在一些实际运用中也体现了其良好的性能与可观的加速效果,Silva 等在空气动力学计算中尝试引入ROM 下的CFD 算法,取得了一定的成果[6]。然而,在早期的相关研究中大部分ROM 的结构较为简单,影响了其性能。
随着机器学习类方法的飞速发展,相关算法在各领域内应用广泛,在CFD 领域中也是如此。利用ROM 类算法后,相关模型的复杂度得到了提升,模型性能也得到了提升。在热对流问题的研究中,Yasin 等提出利用支持向量机(SVM, support vector machine) 对温度分布和流场进行预测[7]。 而在针对粒子法的数据驱动研究中,Ladicky 等引入回归森林(regression forests) 方法,近似模拟粒子行为模式,循环使用粒子预测模型完成对流场长时间运行的模拟[8]。
上述机器学习方法较为传统,近年来的研究证实其效果不如包括深度学习算法在内的新型机器学习方法[9]。由Guo等提出的网络模型完成从边界条件直接到稳态结果的预测过程[10]。这一直接预测稳态结果的思路精度较高,但是对于非稳态问题以及需要关注流场发展过程的稳态问题并不适用。由Tompson 等运用卷积神经网络(CNN,convolution neuron network) 取代压强求解器,通过取代迭代过程降低了计算资源消耗[11]。然而,在显式LBM 算法中并没有一个迭代求解单个方程的子过程,也就导致这种思路不适合运用到LBM中。在对LBM 压缩提速方面,Hennigh 提出了Lat-Net,利用深度学习模型对LBM 过程进行信息提取完成了一个神经网络组成的流场模拟算法,在网络中特别关注了对边界条件信息的保持[12]。但是,由于网络预测产生的误差较大,在反复迭代中误差累积较为明显,导致结果有一定的偏差。同时对于边界条件不鲜明的问题,该模型的效果有待验证。
本文中采用深度学习模型对原有LBM 中的计算过程进行替换,以一个模型计算代替原有算法的多个迭代过程,达到减少迭代次数的目的,本文中将该模型称为压缩LBM ( C-LBM, compressed LBM) 模型。本文所采用的网络应用领域为图像生成领域,在相关领域内已有一些成熟的相关研究[13-15]。而,本文采用了一个较为新颖的网络结构。具体来讲,C-LBM 模型是以卷积长短期记忆网络(ConvLSTM, convolutional LSTM network)[16]组建的编码网络和以残差神经网络(Resnet, residual network)[17]组建的解码网络为主体的深度神经网络模型,通过输入带有时间和空间双重维度的流场信息取得对跨越多个迭代后流场情况的预测结果。该模型的优势在于具备适应非稳态问题和稳态问题过程模拟的能力,同时具有较好的精度。
1 Lattice Bhatnagar-Gross-Krook(LBGK)模型
LBM 中主要研究的流场物理量是粒子速度分布函数,通过刻画粒子速度分布函数随时空的变化,完成对各种宏观物理量变化情况的求解。粒子速度分布函数在统计力学中是一个十分重要的基本物理量,常用符号f(x,ε,t)表示。该物理量的定义为:在不考虑粒子的转动而只考虑其平动的前提下,在某一时刻t,在空间中以x为中心的微元dx内,速度处于ε与ε+ dε之间的分子数为fdxdε。在LBM 中粒子分布函数被离散至各个离散速度方向并记为fi,本文使用的针对二维的D2Q9模型中共有9个离散速度方向,各个方向的速度记为ci,fi与ci一一对应[18]。由此,相应的宏观密度和速度为
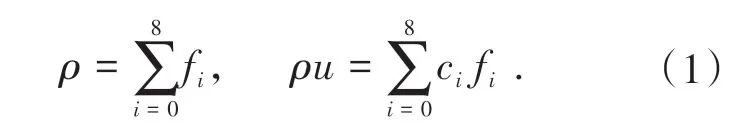
LBGK 模型是基于Bhatnagar-Gross-Krook(BGK) 碰撞模型算子建立的一种简单LBM 模型,其离散形式控制方程为
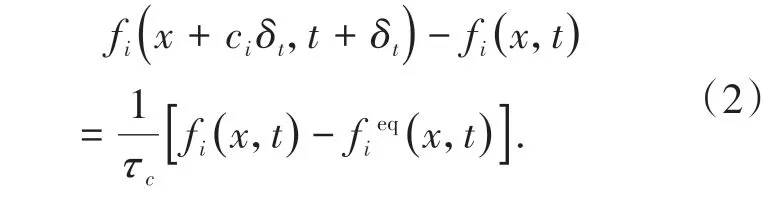
该方程即为LBGK 方程, 其中τc为松弛因子。LBGK 方程包括对粒子迁移和碰撞两方面的描述,在LBM中将这两个部分分开计算,其表达式为
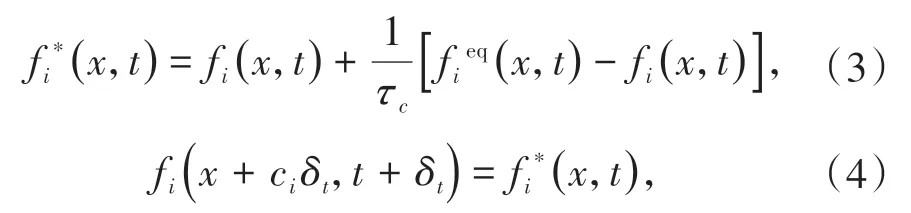
其中公式(3)描述粒子碰撞过程,而公式(4)表示迁移过程[19]。
通过以上关于LBGK 模型的描述不难发现,在给定空间大小(x,y) 下,整个计算过程中的核心物理量,即离散粒子速度分布函数,实际上是一个大小不变的三维数组,其大小为(x,y,9),其中最后一维对应离散速度数,而二维卷积运算所需要的输入规格刚好与这一数组相对应,即前两维表示空间上的长和宽,最后一维为通道数刚好对应离散速度数。由此,本文的网络模型中将原有离散粒子速度分布函数信息通过卷积的形式提取并完成相应计算,而卷积运算速度较快且对原有信息的保全度高,完成运算资源消耗少且能保证一定精度的算法。
2 基于深度学习的压缩LBM模型
2.1 C-LBM模型网络结构
本文中的网络模型主要由ConvLSTM 和Resnet组成。C-LBM 模型的编码部分由ConvLSTM 网络组成,ConvLSTM 对于空间和时间的双重处理能力可以将其视为最适合本文建立预测模型的工具[17]。解码部分由Resnet 组成,由于其拥有抗退化的能力,可以降低本模型的训练难度,使得模型的拟合效果更好[18]。图1 为本文的网络结构图,其中输入记为F(T)和F(T+100),输出记为F(T+1100),该粒子分布函数F(T)(与原LBM 计算完成T次迭代的结果对应) 为
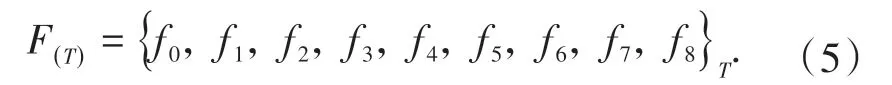
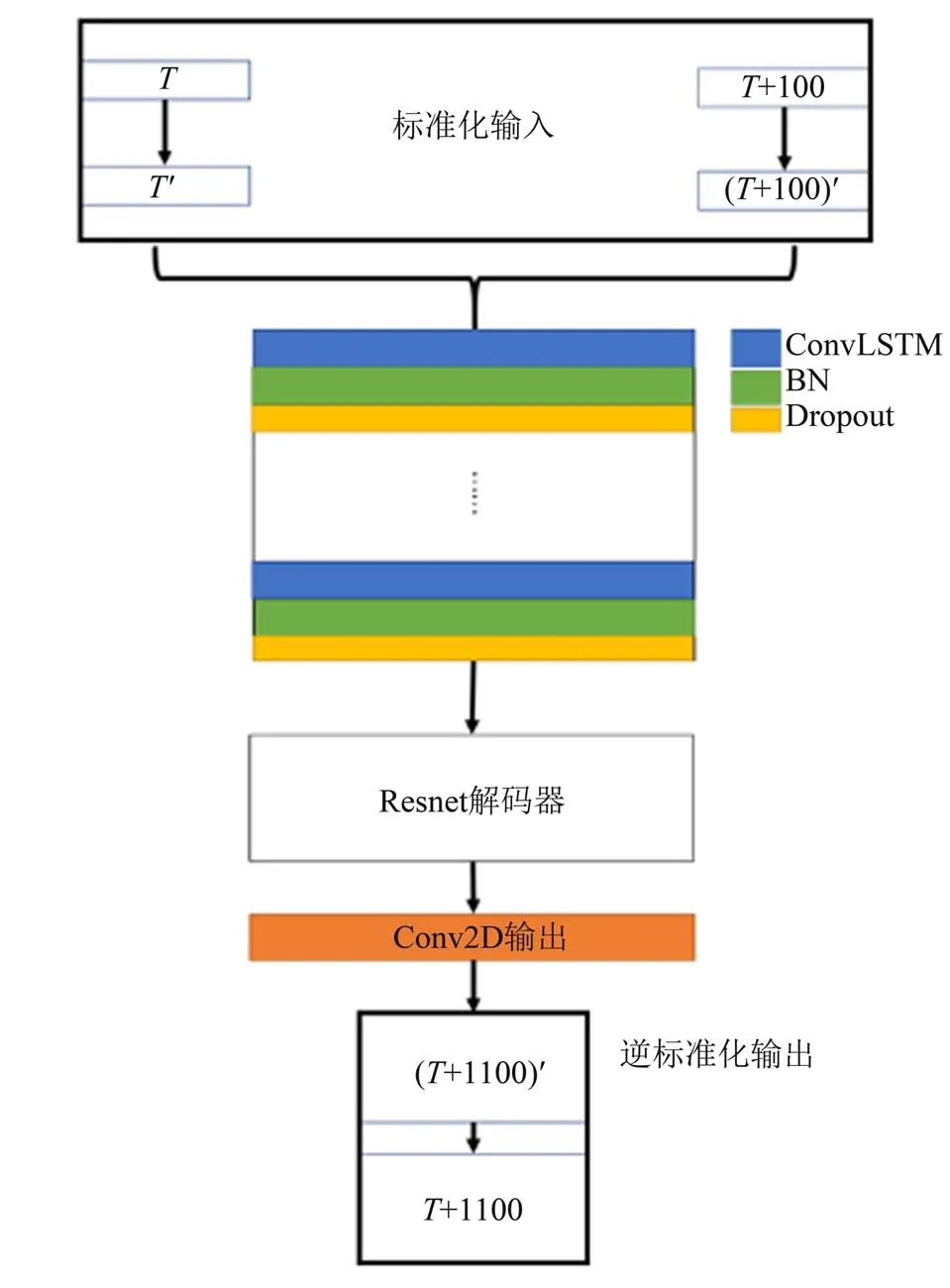
图1 C-LBM模型网络结构示意图Fig. 1 C-LBM model network diagram
该网络的输入为相隔100个迭代、两个时刻的分布函数。对于二维问题,两个输入均为三维矩阵,第一维对应空间长度,第二维对应空间宽度,第三维对应神经网络中通道数。整个预测网络的结构大致包括输入预处理(标准化输入),通过堆累ConvLSTM 层的网络提取特征及拟合,Resnet 解码,卷积层输出以及输出结果还原(逆标准化输出) 五个过程,即从已有分布函数结果抽取时空信息,得到对未来分布函数的预测结果。预处理内容为标准化过程,由于在训练中输出也进行了标准化处理,因此在使用时需对输出结果进行还原处理。具体来讲,这一处理为神经网络数据集标准化中的Z-Score标准化
其中μ为数据集均值,σ为数据集标准差,x为处理前数据而z为处理后数据。同时,ConvLSTM 的状态(stateful) 被设置为真(true), 批次大小(batch size) 被设置为1。对于本文中的stateful 为true的循环神经网络,其网络训练的batch size与模型使用的batch size 大小是相同且固定的。为了构建单次只利用一批数据且内容为两个输入到一个输出的模型,在训练时必须将batch size设置为1。
2.2 C-LBM模型损失函数与优化方法
损失函数(loss function) 在深度学习中有着极其重要的意义,本文针对LBM 的物理背景结合神经网络训练中常用的损失函数,设计了一个针对C-LBM 模型的损失函数,命名为CLBMLOSS,其表达式为
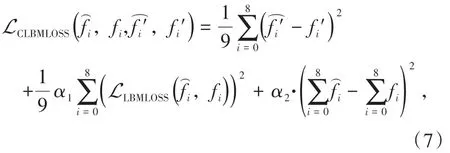
其中表示预处理还原后预测结果,fi表示还原后对应真实值,表示还原前预测结果,表示还原前对应真实值。本文中,系数α1=90,系数α2=10,目的在于使各单项误差数量级接近,保证其均能发挥作用。
CLBMLOSS的第一部分为在神经网络训练中常用的二范数误差MSE,即预测值与真实值相减结果平方的平均值。第二部分被命名为LBMLOSS,其内容为利用真实值与预测值经过碰撞过程的计算结果做差。神经网络中输入和输出的分布函数均是计算到每个迭代的末尾时的结果,即完成了碰撞和迁移两个过程的计算后得到的结果。由此,可以将这两个输出结果代入再完成一次碰撞过程,这样得到两个碰撞一次后的分布函数结果,如果真实值和预测值完全相同则该误差为零。通过增加该部分误差,带入了LBM 物理背景的信息,包括流场速度输入和雷诺数等。与此同时,这一项误差的引入使得预测值尽可能与LBM 相适应。具体来讲LLBMLOSS计算公式为
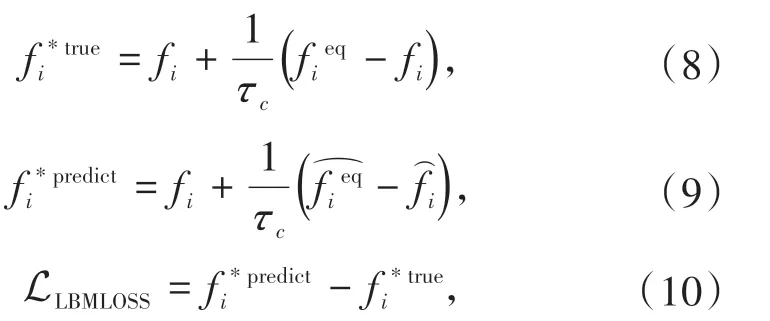
其中为由真实值fi计算得来的平衡态分布函数,而为由预测值计算得来的平衡态分布函数。式(7) 第三项误差内容为将预测值的9 个通道求和,将其与真实值9 个通道求和结果相减,9 个通道和的物理意义是在各个格点处的密度,该误差的意义在于引入一个宏观物理量对模型进行调控。
本文中训练采用反向传播算法(back propagation),该方法由Hinton 等提出。简单的讲,其内容包括激励传播和权重更新两个部分,先正向传播得到输出再反向传播得到响应误差,之后利用误差获得梯度并对权重进行更新,达到训练网络的目的[20]。本文中利用的优化算法为自适应动量的随机优化方法(adaptive moment estimation)[21]。
3 算例实验
本文中采用方腔环流模型完成对模型的训练与测试,该模型被广泛运用于计算流体力学算法的验证中[22]。本文选择方腔环流模型作为实验模型的原因主要有以下几点:首先,方腔环流问题的初始条件和边界条件极为简单,程序设计较为简便;其次,方腔环流模型下的流场特点鲜明,便于结果之间进行对比;最后,方腔环流模型的流场情况随参数变化较为明显,特别是在不同雷诺数下流场变化较为明显,有利于测试模型的泛化能力。值得注意的是,虽然方腔环流问题是一个稳态问题,但是在本文的研究中着重关注整个流场演化过程,而并非仅仅关注计算的最终稳态结果,由此证明该模型对流场发展过程的还原能力以及在非稳态问题中的潜力。
3.1 模型训练
表1为本文生成训练集和测试集时LBM的相关基本物理参数的设定。
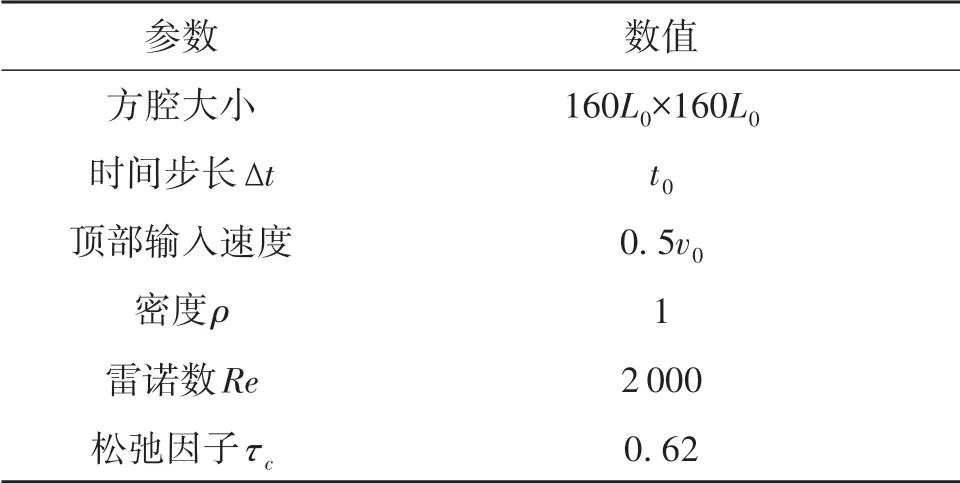
表1 生成流场的物理参数Table 1 Physical parameters of the flow field
表1 中L0、t0、v0分别为单位长度、单位时间和单位速度。本算例中的训练集一共包含345组,测试集一共包括5组,测试集不参与训练过程,每组训练集和测试集中所包含的样本批数相同,均为5批,一组样本内打开stateful 关联。由表达式表示整个训练集,一组训练集或测试集的输入集合GIN和输出集合GOUT为
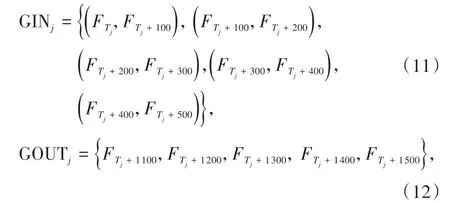
其中j表示组数,j=0,1,2,…,350,Tj表示第j组内第一批输入的第一个时间步对应的原LBM 计算中所需的迭代次数。
为验证ConvLSTM 与Resnet 网络结构以及损失函数CLBMLOSS 对模型性能的影响,本文训练了3个使用不同网络结构和训练损失函数的模型,分别 以“MSE+ConvLSTM+Resnet”,“CLBMLOSS+ConvLSTM”和“CLBMLOSS+ConvLSTM+Resnet”进行标记,在3. 2 的误差分析中也将沿用这三个模型进行相关测试。图2中展示了这三个模型的训练过程中对应损失函数值的下降过程,横坐标为训练轮数。
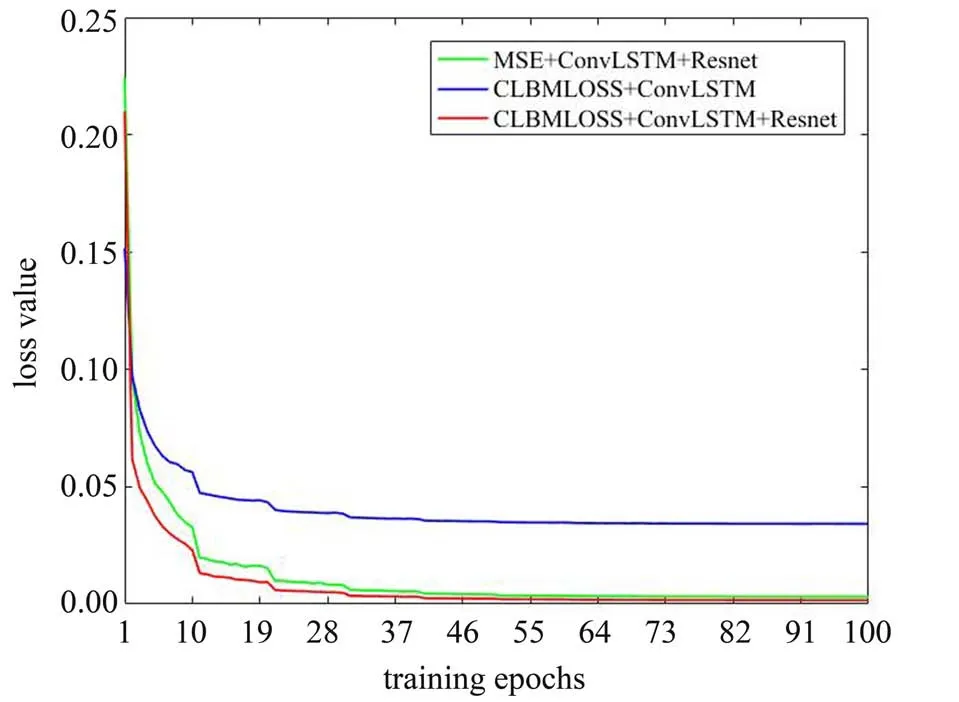
图2 训练中损失函数值下降情况Fig. 2 Loss function value decline during training
图2中,使用ConvLSTM+Resnet 结构后损失函数最终收敛数值明显较低,初步证明了这种结构的模型具有更好的学习能力和抗退化能力。相较于MSE 训练的模型,CLBMLOSS 训练的模型损失函数最终收敛数值略低,表明引入CLBMLOSS 对模型的学习能力没有产生严重影响。同时CLBMLOSS 包括MSE 部分,同一结果下前者必然大于后者,而图2中在模型收敛后使用CLBMLOSS 训练的模型损失函数值更低。由此可知,若使用相同评价标准,利用CLBMLOSS训练的模型精度更高。
3.2 误差分析
误差分析部分首先验证模型在Re=2 000 的测试集上的精度。本文模型的重要创新点的第一部分是结合ConvLSTM 与Resnet 的网络结构,第二部分是针对LBM 物理背景设计的损失函数CLBMLOSS,以下也将检验这些创新点对模型精度带来的增益效果。
Re=2 000 的实验集共6 组,每组5 批样本,总共30 批样本,将这些样本依次编号为1 到30。由此1 到5 为一组,6 到10 为一组,依此类推,各组之间的状态(state) 不能传递,即每隔5 批就将state 清零。以下利用均方差总体评价模型输出精度情况,令函数F (x,y,i) 表示位置为(x,y) 处,全局均方差计算公式为
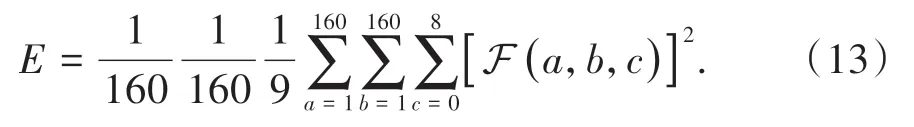
图3为各个不同网络结构和优化方法下的全局均方差值,横轴为各批次预测输出对应普通LBM结果的迭代次数,即第一组样本为1 800、1 900、2 000、2 100和2 200次迭代结果,依此类推。
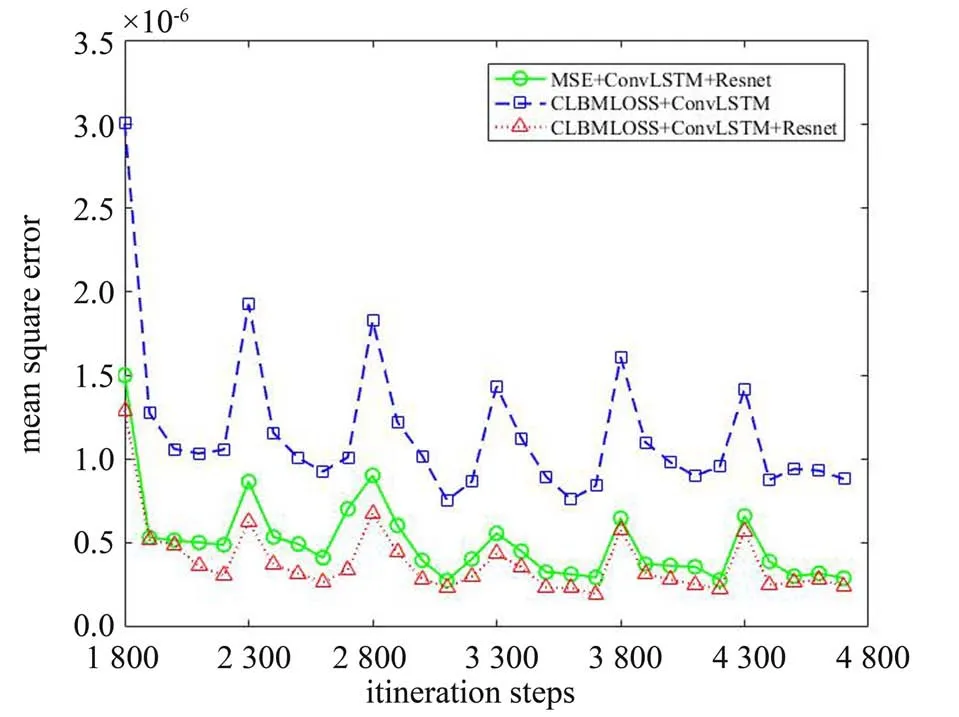
图3 Re=2 000全局均方差误差Fig. 3 Global mean square error when Re=2 000
图3中,添加了Resnet 解码器的网络在误差上明显低于未添加解码器的网络,表明了Resnet 解码器对模型精度提升的贡献。同时,利用CLBMLOSS对模型预测精度产生了一定幅度的积极影响,这也证明了使用CLBMLOSS 在提升预测准确性上的意义。从图3中不难看出,每组的第一批样本的预测精度弱于同组内其他批次的,这是由于第一批预测模型中还没有状态量(state) 的数据,导致预测的根据不足,从第二批预测开始模型同时使用本批数据和state 量,精度较高,这也提示在使用模型时最好用第二批及以后的数据作为最终输出结果。
下面,通过速度场标量图4比对真实结果,并展示来自真实值与预测值之间的残差图,同时附加对居中行和居中列结果的比较。以下误差分析均在实验集5 上(对应普通LBM 算法完成2 200 次迭代结果) 进行,输出结果对应普通LBGK 算法完成2 000 次迭代。其中,图4 (a1) 与4 (a2) 为输入数据所求得的速率标量场;图4 (b) 为输出结果对应的常规LBM 速率标量场即真实值;图4(c1)、4 (d1) 和4 (e1) 为各模型预测的速率标量场;图4 (c2)、4 (d2) 和4 (e2) 为各模型预测值与真实值之间的绝对误差。
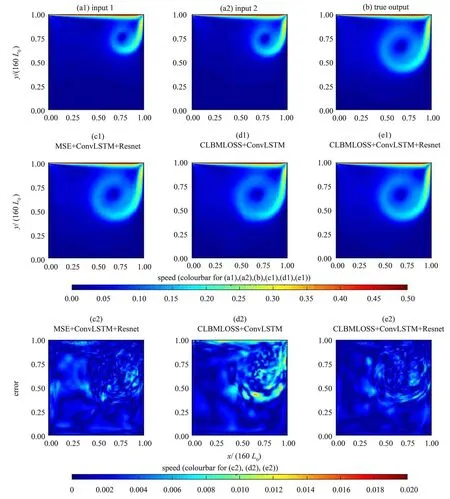
图4 Re=2 000时全流场的可视化结果与误差分析Fig. 4 Visualization results and error analysis of the flow field when Re=2 000
从图4 中不难看出,同时利用了ConvLSTM+Resnet结构和CLBMLOSS优化函数的模型有更高的精度。 首先, 从对比中可以看出, 具有Conv-LSTM+Resnet 结构的模型最大误差和整体误差都明显小于没有这一结构的模型,这体现了Resnet 提高了模型复杂度和学习能力;其次,具有CLBMLOSS 优化函数的模型零误差及极低误差区域面积更大,这是由于该损失函数的引入增加了物理信息,引导模型加强识别流场中的低速部分,同时提高各个通道之间的关联性,从而有效地降低了误差,尤其是低速区域的误差。为了进一步验证,以下对比在居中行与居中列处,各个模型预测的速率结果和真实速率结果,同时加入绝对误差图像,即真实值与预测值的绝对差值。图5(a1)与5(a2)展示了结果曲线,图5(b1)与5(b2)则是误差曲线图。
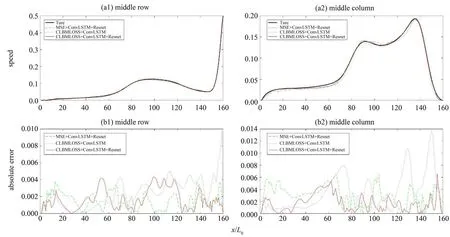
图5 Re=2 000时居中行与列可视化结果与误差分析Fig. 5 Middle row and column visualization results and error analysis when Re=2 000
图5进一步证明了从二范数误差图中所得出结论的正确性。加入Resnet 降低了最大误差,而CLBMLOSS 的引入对低速区域误差降低有较好作用,在高速区有无CLBMLOSS 对精度的影响并不明显,不过在高速区所有模型的误差相较于真实值都很小,影响并不明显。总而言之,该实验体现了ConvLSTM 层和Resnet 层组合网络以及CLBMLOSS损失函数的强大功效。
为了进一步验证本文中各模型在泛化问题中的表现,本文选用了Re=4 000 的非训练雷诺数测试集,对该测试集下的精度进行了校验。同样的,实验集共6组,每组5批样本,总共30批样本,将这些样本依次编号为1 到30。图6 是不同网络结构和优化方法下的全局均方差值,横轴为各批次预测输出对应普通LBM 结果的迭代次数,即第一组样本对应1 900、2 000、2 100、2 200 和2 300 次迭代结果,依此类推。
从图6 中可以看出,CLBMLOSS 的引入在提升模型泛化能力中的效果较为明显,引入CLBMLOSS损失函数的两个模型预测精度更高,这是由于加入CLBMLOSS 后在优化过程中引入了雷诺数信息,有效增强了模型物理泛用性。在这一部分实验中,加入Resnet 的网络只在约半数的批次中有更高精度。在这一点上,我们认为可能网络结构复杂化增大了过拟合的程度,不过基于上一个实验中Resnet的增强效果,我们依然认可引入Resnet的提升意义。
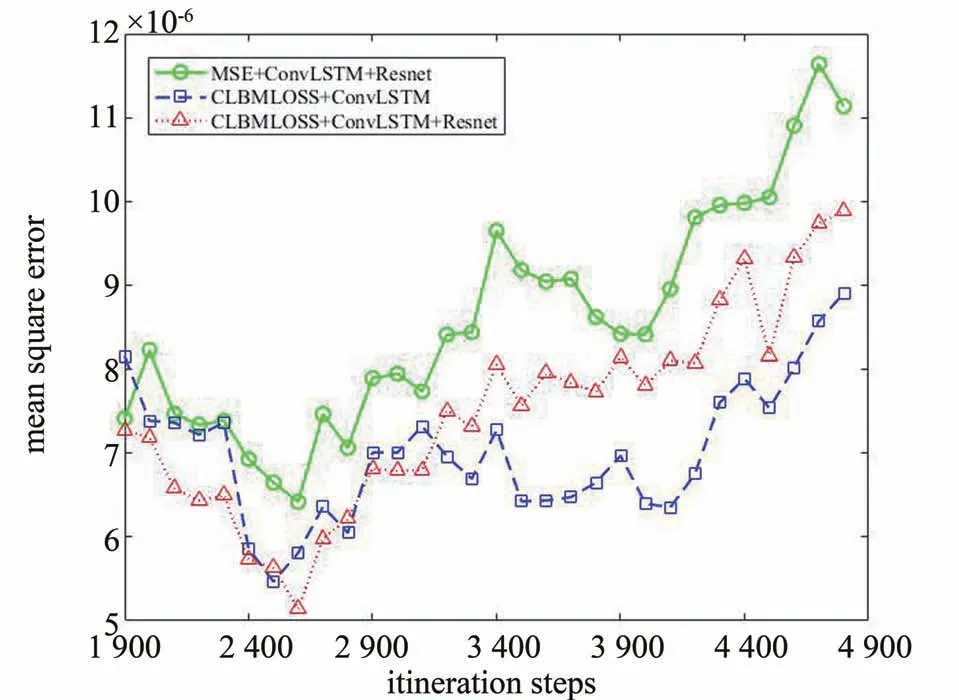
图6 Re=4 000全局均方差误差Fig. 6 Global mean square error when Re=4 000
同样的,图7为预测结果精度和真实值与预测值之间的残差,同时附加对居中行和居中列结果的比较。以下误差分析均在实验集25 上进行(对应普通LBM 算法完成4 200个迭代)。同样的,图7(a1) 与7 (a2) 为输入数据所求得的速率标量场,图7 (b) 为输出结果所对应的常规LBM 速率标量场即真实值,图7 (c1)、7 (d1) 和7 (e1) 为各模型预测的速率标量场,图7 (c2)、7 (d2) 和7(e2) 为各模型预测值与真实值之间绝对误差。为了进一步验证,同样对比在居中行与居中列处各个模型的预测速率和真实速率,同时加入绝对误差图像,即真实值与预测值的绝对差值。图8(a1) 与8 (a2) 展示了结果曲线,图8 (b1) 与8(b2) 则是误差曲线图。
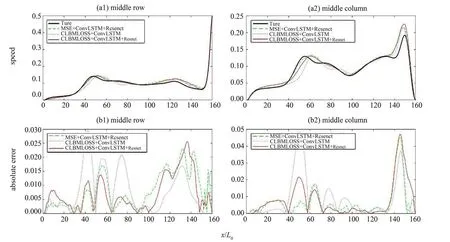
图8 Re=4 000居中行与列可视化结果与误差分析结果Fig. 8 Middle row and column visualization results and error analysis when Re=4 000
从图7中可以明显看出CLBMLOSS 在模型泛化能力方面的提升,总体误差和最大误差都明显下降,同时在上个实验中提到的对低速区精度的优化效果也依然存在。
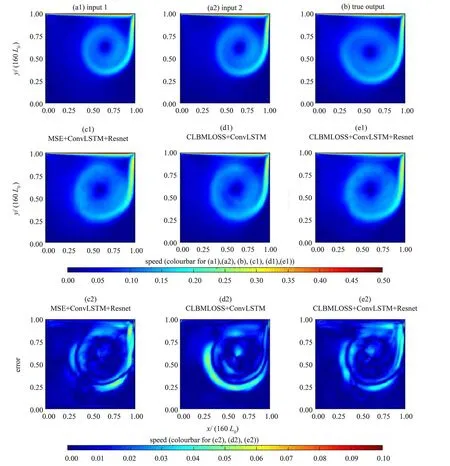
图7 Re=4 000时全流场可视化结果与误差分析结果Fig.7 Visualization results and error analysis of the flow field when Re=4 000
从图7 和图8 中的误差数据可以看出,Conv-LSTM 和Resnet 组成的网络结构以及CLBMLOSS 损失函数对网络精度的提升有积极意义;同时,本模型具备一定程度的多雷诺数泛化能力,在不利用Re=4 000 训练集训练的前提下,仍然可以应用于相关算例。
3.3 计算压缩效果分析
本文测试平台为Intel (R) Core (TM) i7-9750H CPU@ 2. 60Hz 以及NVIDIA GeForce GTX 1660 Ti。这一平台属于典型的家用机配置,该测试环境有利于模拟本模型算法在受限制的计算机能下的计算能力,这也是本算法的设计目标应用领域,即针对计算能力有限的设备完成具备严谨物理背景的流体仿真。表2中展示了不同雷诺数下不同时段利用模型完成计算和原有算法计算的耗时对比,时段由完成的迭代数量表示。
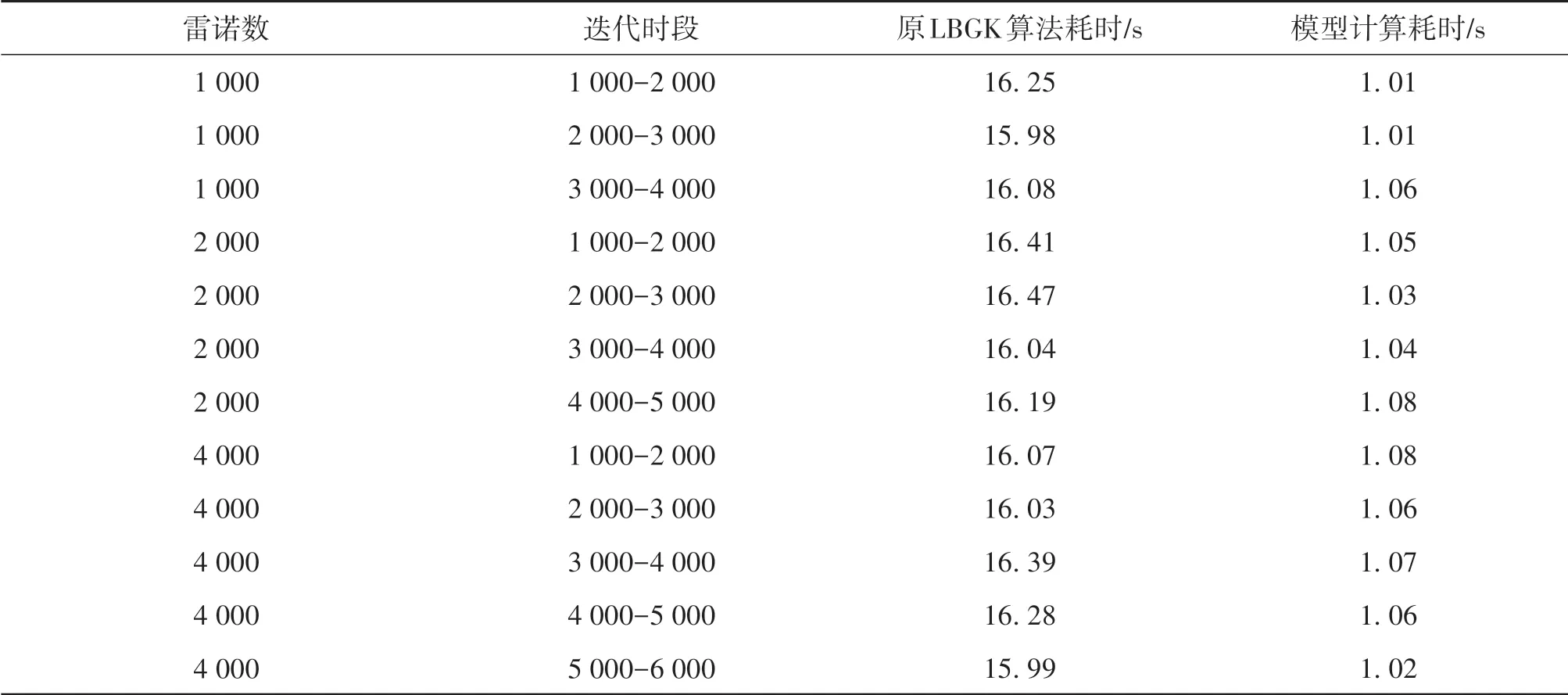
表2 耗时对比Table 2 Time-consuming comparison
从表2中不难看出,计算耗时与计算区间和雷诺数并无关联,原串行算法耗时约为模型计算的15倍。在评价LBM 的计算效率时引入一个专门量,即每秒百万格子更新数(MLUPs, million lattice updates per second),其计算公式为
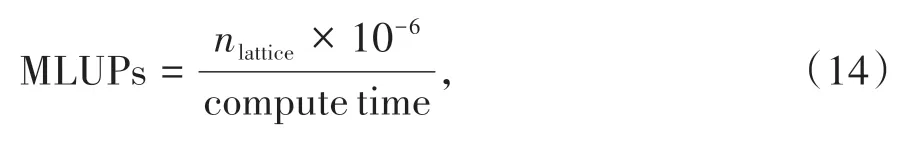
其中nlattice为格子单元的数量,compute time 为计算时间。本文中的算例下nlattice=25 600,表3 列出了C-LBM 模型下连续预测计算过程的各项耗时及由此计算得到的MLUPs。对于C-LBM 模型由于其计算一次相当于普通LBM 计算1 000 次,所以在计算其对应的MLUPs时还需要考虑到这一对应关系。

表3 计算效率实验结果Table 3 Calculation efficiency experiment results
在家用级别平台上,本文新模型的计算效率为串行LBM 程序的15 倍左右。由此可见,相较于串行LBM 程序,本文提出的新模型在减小计算资源消耗方面效果显著,该算法的实验结果达到预期。
4 结 论
为提高传统LBM 的计算效率,本文实现了对LBM 原有计算过程的简化压缩,克服LBM 在消耗计算资源方面的劣势。基于以上目标,本文利用ConvLSTM 层和Resnet 层等深度学习网络结构设计了一个预测网络模型并命名为C-LBM 模型,该模型通过输入早期的粒子分布函数数据对跨越多个迭代后的粒子分布函数进行预测。完成模型训练后,本文对该模型预测精度以及计算效率进行了分析与验证,得出了该模型具备基本可靠性和一定泛化能力的结论,并达到了大幅压缩计算资源消耗的目标。
