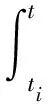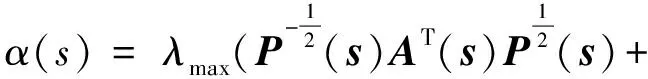线性随机时变系统的有限时间稳定性研究*
2021-10-21吴小太
余 勇, 吴小太
(1.安徽工程大学 电气工程学院, 安徽 芜湖 241000; 2.安徽工程大学 数理学院, 安徽 芜湖 241000)
0 引 言
近些年,针对时变系统控制问题的研究越来越受到控制领域专家的关注,并成为被广泛讨论的热门问题之一,研究时变系统的稳定性是系统设计的重要问题。Zhou[1]提出了一类线性时变系统的渐近稳定性、指数稳定性和一致指数稳定性的充要条件。针对线性时变系统的研究虽然取得了一些进展,但现有的结果大多局限于线性时变系统的稳定性问题。Zhang[2]研究了一类线性时变系统的采样数据控制,根据比较原理和Halanay不等式,推导了闭环系统的全局一致指数稳定性和全局一致渐近稳定性的新判据。
在实际生活中的系统,往往会受到一些不可预测的随机因素影响,如果忽略随机因素对实际系统的影响,可能会导致建模的系统性能不佳,难以刻画系统的实际运行状态。因此,需要建立随机线性时变系统模型,并研究其相关性质。Wu[3]研究了脉冲非线性随机系统的输入状态稳定性,这里连续时间动态系统是时变的,系统在一部分时间区间上稳定,而在其他时间区间内不稳定,文中给出了一些基于Lyapunov函数方法的脉冲随机非线性系统的充分条件。
Kamenkov[5]在1953年首先提出了有限时间稳定性概念,经过多年的发展,关于有限时间稳定性研究已取得了大量的结果[6-13]。Zhou[6]提出了时变系统的随机时间稳定性研究方法,基于线性矩阵不等式的优化方法来求解控制增益矩阵;Amato[7]考虑了连续时间线性系统的有限时间稳定,设计了动态输出反馈控制器的充分条件,保证了闭环系统的有限时间稳定性。
综上所述,Zhou[6]提出了一类线性时变系统有限时间稳定性的研究方法,并通过线性矩阵不等式方法给出了系统的反馈控制器。然而,该方法并不能用来研究随机时变系统的有限时间稳定性;同时,Amato[11]研究了随机线性系统的有限时间稳定性,但Amato[11]的反馈控制设置并不能很好解决时变系统的反馈控制器设置问题,所给的反馈控制器很难在实际操作中加以应用。因此,本文结合Zhou[6]逐段分析的方法和随机分析技巧,研究了随机线性时变系统的有限时间稳定性,并给出了系统反馈控制器的设置方法。
1 相关定义
相关记号:记R={-∞,+∞},R+=(0,+∞),P∈Rn×n,P(t)∈Rn×n分别为矩阵与矩阵值函数。对于矩阵P,P>0表示P为正定矩阵,PT表示矩阵P的转置,λmin(P)和λmax(P)分别表示对称矩阵P的最小和最大特征值;设P=aij,Q=bij,对任意的i,j=1,2,…,n,有aij≥bij,则称P≥Q;In表示n维单位矩阵;设ω(t)表示n维标准布朗运动,E(·)表示随机变量的期望。
研究如下随机线性时变系统:
dx(t)=A(t)x(t)dt+H(t)x(t)dω(t)
(1)
其中t∈[0,T],T∈R+;x(t)∈Rn,系统状态x(t)∈Rn,系统初值x(0)=x0,矩阵值函数A(t),H(t)∈Rn×n。下面将研究系统式(1)的随机有限时间稳定性,首先给出有限时间稳定的定义如下:
定义1[13]假定Φ=[0,T],R∈Rn×m,Γ(·)为正定矩阵。对式(1),若对于任给的x0与t∈Φ,有
则称系统式(1)满足随机有限时间稳定性。
定义2[3]对于函数V:[0,∞)×Rn→R+,对式(1)定义算子V:[0,∞)×Rn→R,如下:
V
(
t
,
x
(
t
))=
V
t
(
t
,
x
(
t
))+
V
x
(
t
,
x
(
t
))
A
(
t
)
x
(
t
)+
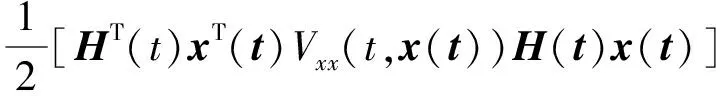
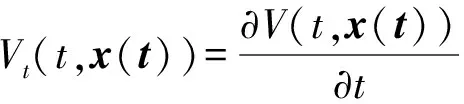

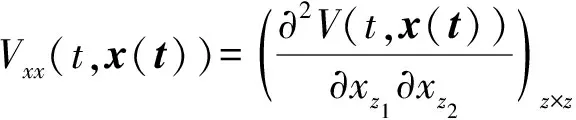
0≤
z
1
,
z
2
≤
z
2 主要结论
定理1 给定一个初始时刻t0≥0,R∈Rn×n,正定矩阵Γ(t):[t0,t0+T]→Rn×n,且满足Γ(t)
P(t)=Pi,∀t∈[ti,ti+1],i∈{0,1,…,r-1}
若有
(A1) 对于所有t∈[t0,t0+T],有
P(t)≥Γ(t),P0 (2) (A2) 对于i∈{0,1,…,r-1},有 (3) 这里 (4) (A3) 对于i∈{0,1,…,r-1},有 成立,则式(1)满足有限时间稳定性。 V(t,x(t))=zT(t)z(t) (5) 注意到P(t)=Pi,对于∀t∈[ti,ti+1],i∈{0,1,…,r-1},由定义2知,对∀t∈[ti,ti+1],有 由式(4)知 (6) 对式(6)两边取期望,可得 (7) 由式(7),通过简单整理,可得: E[U(t,x(t))]≤E[U(ti,x(ti))],t∈[ti,ti+1] (8) 由式(3)与式(8),对∀t∈[ti,ti+1],有 E[V(t,x(t))]≤E[V(ti,x(ti))] (9) 由于假定的Lyapunov函数满足分段连续性,在每一个分段点ti处,函数可能不连续。下文将给出V(ti,x(ti))的上界估计。由式(5),有 (10) 由式(8),可得 (11) 结合式(10)和式(11),有 由V(t,x(t))的定义,对于∀i∈{0,1,…,r-1},有 (12) 对式(12)右边进行整理 (13) 结合式(12)和式(13),即得 在其总结部分(Ⅰ卷,53页),委员会报告得出结论,“过去的连续运动产生了裂谷的独特地貌特征……毫无疑问在每种情况下都有强度或大或小地震的作用。1906年4月18日的地震,就是由于这条断层线上运动复发的结果。”(注:由于该断层通常包含在线性的、明确的宽为0.8~1.6km的山谷中,报告通常将该断层带称作圣安德烈斯裂谷)。委员会成员对这些地震复发细节的关注和信心使他们建立了两个 “用于测量圣安德烈斯断层上将来的运动”的小台阵(Ⅰ卷,152页)。 E[V(ti,x(ti))]≤E[V(t0,x(t0))]i∈{0,1,…,r-1} (14) 综合式(9)和式(14),有 E[V(t,x(t))]≤E[V(t0,x(t0))] ∀t∈[t0,t0+T] (15) 故由式(2)和(15),可得 E[xT(t)Γ(t)x(t)]≤E[xT(t)P(t)x(t)]=E[V(t,x(t))]<1 故式(1)满足随机有限时间稳定性。 本节中,将采用Zhou[6]类似的方法,考虑系统式(1)的控制器设置问题。假定具有反馈控制器的随机线性时变系统如下: dx(t)=A(t)x(t)dt+B(t)u(t)dt+H(t)x(t)dω(t) (16) 状态反馈u(t)=K(t)x(t)。 定理2Q(·),L(·)为分段连续的矩阵值函数,并且满足 Q(t)=Qi∈Rn×n,∀t∈[ti,ti+1)i∈{0,1,…,r-1}L(t)=Li∈Rn×m,∀t∈[ti,ti+1)i∈{0,1,…,r-1} (17) 假定 则系统式(16)可写成 dx(t)=Ac(t)x(t)dt+H(t)x(t)dω(t) 这里Ac(t)=A(t)+B(t)L(t)Q-1(t)。若有 (A4) 对于∀t∈[t0,t0+T),有 Q(t)≤Γ-1(t),Q0>R-1 (A5) 对于i∈{0,1,…,r-1},有 这里 α(s)=λmax(AT(s)+Q-1(s)LT(s)BT(s)+Q(s)A(s)Q(s)+Q-1(s)B(s)L(s)+HT(s)Q-1(s)H(s)Q(s)) (A6) 若α(s)满足 (A7)Hi满足 Hi≤δiI (18) 成立,则随机线性时变系统式(16)存在随机有限时间稳定的反馈控制器。 证明设Q(t)为分段连续的函数值矩阵,且满足 P(t)=Q-1,∀t∈[ti,ti+1),i∈{0,1,…,r-1} 由条件(A4)可知条件(A1)成立。对于∀t∈[t0,t0+T],有 所以由条件(A5)可以推出条件(A2)成立。因为Qi,i∈{0,1,…,r-1}正定,能得到 根据式(18),可得 (19) 由条件(A6)可以推出条件(A3)成立。于是,由定理1可知,随机时变线性系统式(16)满足随机有限时间稳定性。 定理2提供了系统式(16)的控制器设计充分可解条件的存在性。根据式(17),如果定理2中的条件能被满足,则能得到一个状态反馈控制器,对于分段连续常数L(·),Q(·)仍然很难实现。因此,下面基于线性矩阵不等式,设计了一类线性随机时变系统的有限时间稳定控制器的算法。 算法设计: (1) 对于初始时刻t0,选择t1>t0,求解下列带有决策变量L0,Q0的LMIs(线性矩阵不等式)。 Q0>R-1Q0≤Γ-1(t),∀t∈[t0,t1)A(t)Q0+Q0AT(t)+L0BT(t)+B(t)L0+δ2Q0≤0,∀t∈[t0,t1) (20) 寻找L0,Q0,满足式(19),如果式(19)不满足,则重新选择t1。 (2) 对于时刻ti,选择ti+1>ti,求解下列带有决策变量Li,Qi的LMIs(线性矩阵不等式)。 Qi≤Γ-1(t),∀t∈[ti,ti+1)A(t)Qi+QiAT(t)+LiBT(t)+B(t)Li+δ2Qi≤0,∀t∈[ti,ti+1)Qi≥RiQi-1 其中 寻找Li,Qi,满足式(20),如果式(20)不满足,则重新选择ti+1。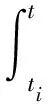

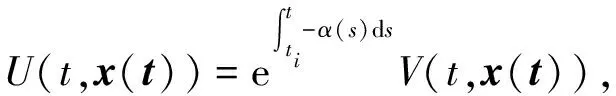
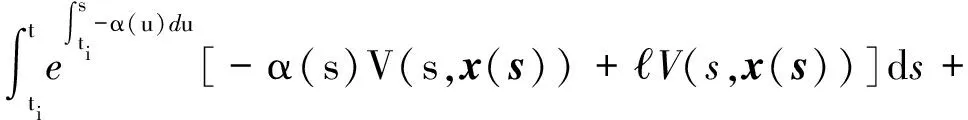

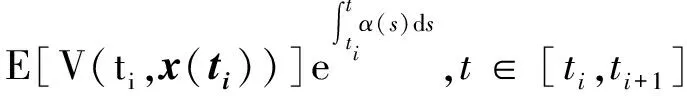
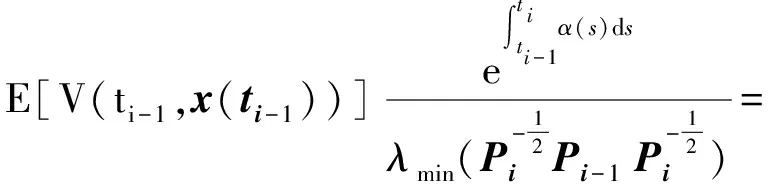

3 控制器设计