基于改进蚁群算法的CVRP问题研究*

程 亮， 干宏程**， 刘 勇

(1.上海理工大学 超网络研究中心,上海 200082;2.上海理工大学 管理学院,上海 200082)

0 引 言

物流，即物的流动，企业通过使用物流的各项基本功能来为客户进行服务。在世界经济快速发展的今天，中国的物流行业也得到了迅速的发展。但由于各种因素的限制如：基础设施不完善、路线布局不合理、人员管理不到位等等，导致了一系列不必要的损失，损害了企业的经济利益。其中，大部分企业损失最大的部分依然在于运输上，因此对于物流运输中车辆路径的优化研究是十分有必要的。

VRP(Vehicle Routing Problem)问题是由DANTIZG教授[1]在1959年提出来的，归属于NP-hard问题。从那时起，对VRP问题的求解一直是研究的热点。马良等[2]是最早一批研究蚁群算法的学者，并将蚁群算法带入组合优化问题中，为后续VRP问题的研究做出了重要贡献。胡祥培[3]提出了新型的环形VRP问题并对其进行了建模与求解。刘冉[4]研究了半开放式多车场问题，并通过三种不同类型的求解算法对结果进行了对比分析。冀德刚等[5]通过将k-means聚类与人工鱼群算法相结合来解决物流配送问题，并通过实例验证了算法的可行性。邓灵斌等[6]研究了果蔬配送的实例，并通过蚁群算法对其进行了求解。马秋卓等[7]调研了市区内快递公司，提出了多车辆VRP问题并把碳排放纳入了需要考虑的因素里。郭咏梅等[8]研究了带有时间窗因素的应急物流，同时使用了算法对问题进行了求解，具有很大的实际应用价值。芦娟等[9]通过禁忌搜索算法对需求依背包拆分的VRP问题进行了求解，验证了算法的有效性。罗鹏[10]通过对蚁群算法进行改进，将其运用到铁路联合路径的规划上并取得了良好的效果。罗梓瑄[11]使用了蚁群算法对CVRP问题进行了求解，并考虑了各种参数之间的影响。MING[12]对具有单元需求的车辆路径问题的指数多插入邻域进行了扩展分析，提升了算法的性能。PIRMIN[13]研究了人的行为策略对VRP问题的影响，考虑了众多现实因素，具有很大的研究价值。虽然国内也不断涌现出与现实实例相结合的VRP问题，但基于我国物流发展的现状，对比国外研究的差距，基础设施的布局不够完善导致大部分国内学者研究的VRP问题依然采用的是基准案例。因此研究的重点就放在了求解方法上，通过不断对算法进行优化与改进，以获得更加满意的可行解或者最优解。通过对CVRP问题进行分析，建立了以总成本为目标的数学模型，并对基本的蚁群算法进行改进，插入轮盘赌运算和2-opt优化算法，提升算法的性能。并通过对比基本ACO算法以及遗传算法的运行结果，验证了算法的可行性和有效性，为更好地解决与VRP相关的问题如FSVRP、VRPTW等问题提供了一定的理论依据与参考价值。

1 车辆路径问题概述

CVRP问题的定义：VRP问题是指在一定的区域范围内，由已经确定好的配送中心向分散在各地的客户提供服务，所有的车辆都是在满足客户需求的约束条件下进行配送，并在配送完成后返回配送中心的过程，具体过程如图1所示。

其中配送中心的位置与客户位置是固定不变的，配送中心所拥有的车辆数目与每辆车的最大容量限制也是已知的。需要在配送之前合理的计划配送路线与运输方式，使得整个过程达到运输成本最小、运输距离最短、运输车辆最少等目的，从而有利于提高企业的物流效益并降低物流成本。

图1 车辆路径问题示意图

1.1 车辆路径问题基本模型

1.1.1 约束条件

(1) 所有的车辆必须从配送中心出发，服务完成后，必须返回配送中心。

(2) 每一个客户点有且只有一辆车可以进行配送服务。

(3) 配送中心的车辆具有相同的最大载重并且行驶时为均速行驶。

1.1.2 基本符号说明

m为配送中心拥有的车辆数。C为车辆的最大载重。qi为客户点i的需求量。cij为从点i到点j的总费用。

决策变量：

i≠ji,j=0,1,2,…,n

即车辆k在服务客户点i之后，紧随着服务了客户点j，此时值为1。

i=1,2,…,n;k=1,2,…,m

即客户点i是由车辆k进行配送，此时值为1。

1.2.3 数学模型

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

xijk=0或1

(9)

yki=0或1

(10)

目标函数式(1)要求总运输成本最低；约束式(2)表示每辆车的容量限制；约束式(3)表示每个客户点仅有一辆车进行服务；约束式(4)表示所有车辆服务完后返回配送中心；约束式(5)-式(7)保证形成闭回路；约束式(8)为网络流平衡条件；式(9)与式(10)为0或1变量。

2 改进的蚁群算法

其中：τij表示城市i、j之间的信息素浓度；ηij表示城市i、j之间的启发式信息；α表示信息素在蚂蚁的移动过程中的相对重要性，当α=0时，蚁群的移动方式会按照启发式信息进行，即蚂蚁将要选择的城市仅仅考虑两个城市之间的距离大小。β表示启发式信息在蚂蚁的移动过程中的相对重要性，当β=0时，蚂蚁的移动方式会按照信息素来进行，这样会导致蚁群的路径固定下来，难以寻找到最优解。

由上可以看出蚁群选择城市的主要影响因素是城市间的信息素浓度，信息素浓度过低就会造成比较长的运算时间，信息素浓度过高又会加速收敛，得不到全局最优解。因此通过对算法进行优化来提升算法的性能。

2.1 轮盘赌运算

轮盘赌运算是遗传算法中会使用到的一种局部优化方法，以信息素浓度作为参考因素，但又通过随机数降低了信息素浓度的相对重要性程度，从而扩大了蚁群可以搜索的范围，避免快速收敛的同时更有概率获得全局最优解。

2.2 2-opt算法

运用轮盘赌运算会增加算法本身的时间复杂度，因此我们通过2-opt算法来提升蚁群算法运行的性能，即对第一次得到的路径进行二次处理，进行城市点之间的交换运算得到新路径，再进行比较得到最优路径。

以下是信息素更新规则如下：

局部信息素更新：

τij(t+1)=ρ·τij(t)+△τij(t,t+1)

全局信息素更新：

τij(t+n)=ρ·τij(t)+△τij(t,t+n)

算法具体流程如下：

(1) 参数初始化，设置蚂蚁数量m，城市数n，α，β与ρ三个因子，循环次数Nc,最大循环次数Max_Nc，初始化信息素τij=c，计算各个城市之间的距离dij。

(2) 开始循环，Nc=1,每次循环结束Nc+1。

(4) 禁忌表未满就不断重复步骤(3)；否则，计算路径总长度，储存得到的最优解，进行2-opt优化，并将得到的最优解进行比较。

(5) 对蚂蚁移动过的路径上的信息素做挥发处理，并根据蚂蚁走过的总长度来计算新的信息素。

(6) 将存储的路径进行比较，得到我们需要的那条路径，如果运行次数达到设置的最大次数则停止运算；如果没有运行到最大次数，则清除禁忌表中的所有元素，返回步骤(3)再次运行。

3 仿真实验

选取了文献[11]中的基本的ACO算法和文献[12]中的遗传算法、改进的遗传算法来说明改进的蚁群算法的有效性。

文献[11]中基本数据如下:车辆载重C= 6 000 kg,车辆数为6辆，蚂蚁数m=40,Max_Nc=100,α=1,β=3,Q=100,ρ=0.4。同样经过10次运算结果如表1所示。

表1 运算结果表Table 1 Operation result table

10次实验得到的最优解为783.591 km，相较于文献[11]中最优解880.867 km，在最优解上提升了11.04%。同时10次运算的平均值为804.922 km,相较于文献[11]中平均值909.186 km,算法在平均值上提升了11.47%。同时根据表1可知，改进的蚁群算法获取目标值在800 km左右的概率为70%，10次实验最坏解为840.646 km依然优于基本的ACO算法的最优解，说明改进的蚁群算法在性能上有大幅度的提升，获得解的整体质量上完全超过了基本的蚁群算法，能够很好地处理CVRP问题。

最优解783.591 km的车辆路径如下：

路径1: 1-23-27-26-25-24-30-31-22-17-1(车辆满载率：97%)

路径2: 1-16-28-19-21-13-1(车辆满载率：100%)

路径3: 1-20-18-15-29-14-1(车辆满载率：96%)

路径4: 1-6-10-3-2-8-1(车辆满载率：94%)

路径5: 1-12-5-7-11-9-4-1(车辆满载率：80%)

5条路径的车辆满载率均在80%以上，没有造成过多的空间浪费，符合实际。 最优解路径如图2、图3所示，计算结果见表2。

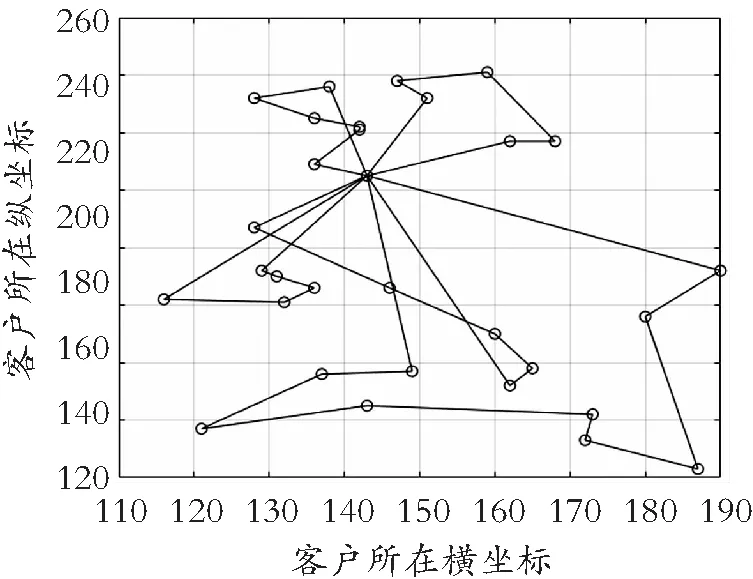
图2 最优路径图

图3 距离变化趋势图

由图3可知：改进的蚁群算法一般在迭代第10次到第20次之间可以找到满意解，最优解也仅在第20次迭代时找到，说明在提升算法搜索性能的同时也节省了算法运行的时间，提高了收敛速度。

文献[12]结果说明(算法基本参数设置与文献[11]相同)。

表2 计算结果比较Table 2 comparison of calculation results

文献[12]中KQGA算法是在遗传算法的基础上采用了优化种群更新操作的手段和2-opt算法，但获得的最优解117.3 km依然高于本文最优解 109.1 km,说明改进的蚁群算法在获得最优解的性能上有很大的提升，降低了陷入局部最优解的概率。

综上所述，改进的蚁群算法相较于ACO算法在性能上有着极大的提升；同时对比遗传算法和改进的遗传算法，可以发现蚁群算法在求解VRP问题有着属于自己的优势，对比结果证明了算法的有效性和可行性。

4 结 论

为解决当今物流企业运输过程中所面临的车辆路径问题，提出了结合轮盘赌运算与2-opt优化算法相结合的改进蚁群算法。通过与传统的蚁群算法进行对比发现，改进的蚁群算法在性能上提高了约11%的同时具有更强的稳定性；对比于遗传算法和改进的遗传算法，求解的精度上也有相当大的提升，因此所提出的算法可以更好地解决带有容量约束的车辆路径优化问题,为相应的企业更好地节省物流成本。