多顶点三角形刚性折纸自由度分析*

张锐浩， 张 帆， 庄彦帅， 张玉辉， 王 锋

(上海工程技术大学 机械与汽车工程学院， 上海 201620)

0 引 言

折纸是一种古老的艺术形式，折纸的命名源自日语词根“ori”和“gami”组合，意思是折叠和纸张,其可以实现不经裁剪和粘接，使二维平面的纸张折叠成三维立体模型[1]。它的运动是连续的且一一对应的二维到三维的映射。折纸可分为刚性折纸和非刚性折纸，假设在折叠过程中，刚性折纸面始终为刚性平面(通常视为连杆)，将折痕视为转轴，则刚性折纸板折叠过程中不发生扭转变形等情况。因此，仅由相邻折叠面的夹角即可决定折纸构型。非刚性折纸则不具有这一假设，认为可以在折纸面内发生扭转、弯曲等变形，可产生形变。由于刚性折纸具有结构巧妙、易于折叠等优点，越来越受到工程师们的关注。例如航天工程中的太阳能阵列[2-3], 在日常生活领域有可折叠餐具[4], 直升机[5]等。为了探索折纸的原理，从而使折纸结构发展出更多的结构，越来越多的学者用数学来揭示其中的原理。

在折纸运动学的研究中，Kawasaki’s提出了单顶点可以平折时夹角之间的基本理论，Maekawa’s提出了山谷折痕分布理论，这两个基本理论成为折纸的基本定理。数值算法[6]、四元数法和矩阵法[7]等被用来分析刚性折纸的可折叠性。Hull[8]研究了单顶点折纸折痕图案能够刚性折叠的一个内在充要条件，为刚性折纸图案拓扑和应用分析奠定了基础。BERRY M等[9]在非欧几里德空间，提出运动高斯曲率的方法研究折纸运动空间。得出了有向顶点的构形空间与高斯曲率的关系。吴和游[9]分别用四元素法和双四元素法建立了折纸机构的运动模型，分析了单顶点或多顶点的折纸图案的平面折叠性，并判断了折纸在折叠过程的自相交性。但是判断折纸机构自由度的方法还是比较少，蔡建国等[11]在刚性折纸机构的自由度的研究中，建立了折纸机构的系统约束方程，并从雅克比矩阵的零空间中计算出了刚性折纸机构的自由度，但是其研究存在局限性，若是机构中存在冗余自由度时，方法不再适用。同时其方法的计算过程较为复杂。

然而，利用邻接矩阵的方法计算刚性折纸机构的自由度，可以简化多顶点刚性折纸机构自由度的运算。首先，介绍刚性折纸的基本条件和基本定理；然后，以计算单顶点刚性折纸机构自由度为基础，拓扑到多顶点三角形刚性折纸自由度的计算。通过折痕与折痕之间的关系，建立邻接矩阵并通过矩阵变换计算刚性折纸机构的自由度；最后，通过软件建模和仿真验证邻接矩阵方法计算的准确性。

1 折纸基本理论

折纸艺术因其能直观展示如何利用折纸来生成连续但有区别的图形，而广泛受到人们的关注。折纸的折叠过程是连续变化的，且能反应折纸图案从二维到三维的映射。折纸图案由一系列的折痕图案组成，包括向上凸起的山折痕(实线)和向下凹陷的谷折痕(虚线)，折纸图案的刚性可折叠性是由一系列的山折痕和谷折痕组合而成，其组合对平折折纸的折叠性起关键性作用。以下介绍折纸的一些基本理论，包括平折的必要条件，有效的山谷折痕分配条件[12-14]。

Kawasaki’s定理1 单个顶点周围的交替角度之和是π，如图1所示。

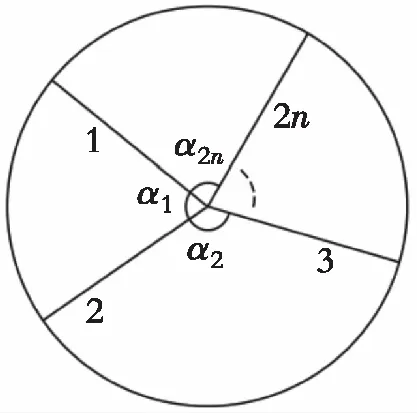
图1 具有n条折痕的单顶点的折痕图案

Kawasaki’s定理2 对于相邻的折痕夹角α1、α2、α3…α2n，假设α2n为其中的最小角，则围成最小角度的折痕必须由一条山折痕和一条谷折痕组成。

Maekawa’s定理山折痕(M)与谷折痕(V)之差为±2，即：

M-V=±2

单顶点折痕所围成的角度之和为2π，如图1所示的单顶点折痕为

α1+α2+α3+…+α2n=2π

2 单一顶点折纸机构自由度研究

在刚性折纸的研究过程中，刚性折纸的折痕视为旋转关节或转动副，刚性纸板则视为连杆(如图2所示)。在单顶点的自由度分析中，无论折痕数多少，单顶点刚性折纸在空间上总是具有3个方向的共同约束力，因此等效机构的秩d为3，根据修改的G-K自由公式[16-17]:

其中，M是机构的自由度，d为机构的秩，n为包括机架在内的构件数，g为运动副数，fi为运动副的自由度，v为多回路并联机构在去掉公共约束后的冗余约束数，z是机构的局部自由度数。

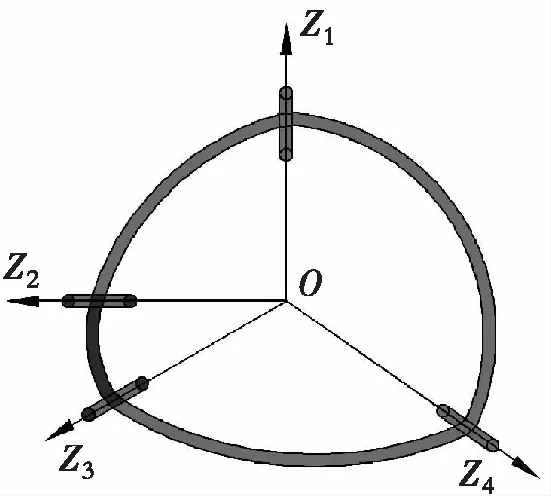
图2 单一顶点4折痕机构

然而，在分析单顶点刚性折纸的自由度时，n为刚性面的面数(杆件数)，g为折痕数，fi为1(通常为转动副)，v和z都为0(一般的单顶点刚性折纸没有冗余自由度和局部自由度)。单顶点刚性折纸顶点可以分为边界顶点和非边界顶点，对于非边界顶点其自由度计算公式为

M=m-3

(1)

其中，M为自由度数，m为折痕数，例如图2所示单顶点4折痕刚性折纸自由度为M=4-3=1。

对于边界顶点其自由度计算公式如下:

M=m-2

(2)

其中，M为自由度数，m为围绕此顶点的折痕数。

3 多顶点刚性折纸机构

对于多顶点刚性折纸机构而言，为了实现折纸的刚性折叠性，每个顶点的运动必须与其相邻的顶点的运动兼容不发生干涉。然而，相较于单顶点刚性折纸机构，多顶点刚性折纸机构获得这样的运动特性是比较难得到的，多顶点刚性折纸机构可以实现刚性折叠的图案是比较少的。因此，分析多顶点刚性折叠机构的自由度是非常有必要的。

利用邻接矩阵方法，分析多顶点三角形刚性折纸图案的自由度，其由单顶点4折痕折纸图案拓扑得到，其图形如图3所示，因其满足平折折纸定理(3个顶点中的任意单一顶点都满足上述平折的必要条件，有效的山谷折痕分配条件)和折纸乘数的积为1[6]等条件而可刚性折叠。对于多顶点三角形折纸图案而言，并不是所有的折纸图案都可以刚性折叠，如图4所示，图4(a)和图4(b)为两种不可刚性折叠情况，已被证明不可严格刚性折叠[18]，虽然满足山谷折痕分布和平折折纸定理，但是因存在 3对相互平行的边而不满足折纸乘数的积为1的条件而不可刚性折叠。

图3 多顶点三角形刚性折纸图案

(a)

(b)

在多顶点三角形折纸图案可刚性折叠的情况下，利用邻接矩阵分析其自由度。邻接矩阵直观展现了顶点之间的连接关系。首先，将多顶点三角形折纸图案封闭，即添加边界，添加边界后的图案如图5 所示，并将顶点由1～9逆时针编号，其中1、2、3为非边界顶点，4～9为边界顶点。则建立的邻接矩阵C0为

矩阵中“1”表示顶点与顶点之间相连，即存在折痕则记为“1”，不相连则为“0”，从矩阵中的每一行或列可以知道每一个顶点有几条折痕围成(例如顶点1有4条折痕)。由于矩阵为对称阵，因此分析时只分析行或列即可。

图5 多顶点三角形刚性折纸边界添加图

通过引入变量Di(i=0,1,2,3，…，9)确定每顶点实现确定运动所需要的驱动，驱动的添加选择从非边界顶点1开始，依次添加驱动(也可以选择从2或3开始，但只能从非边界顶点1、2、3开始)。当邻接矩阵为C0时，变量D0=0(此时并未添加驱动到折纸机构中)，由式(1)和邻接矩阵C0可以计算得非边界顶点1所需的驱动为4-3=1，则邻接矩阵由C0变为C1：

此时矩阵C1中的“1”表示未有确定运动的折痕数(与矩阵C0中的“1”的含义不同),即此折痕未有确定的输入驱动(角度变量)。当非边界顶点1输入了确定的驱动，邻接矩阵C1中的第一列和第一行中的“1”变为“0”。邻接矩阵由C0变到C1引入消元矩阵Ej,n，消元矩阵[10]的表示如下：

消元矩阵是n×n的矩阵，在矩阵中的第j行和第j列中的元素都为0，对角线上的元素为1，左乘矩阵Ej,n使得Ci的第j行中的元素都为0，右乘矩阵Ej,n使得Ci的第j列中的元素都为0，其变换如下所示:

Ci+1=Ej,nCiEj,n

同时变量由D0变为D1，D1=D0+1=1(1表示需要添加的驱动或角度变量)。

然后，继续对非边界顶点2添加驱动，由式(1)和邻接矩阵C1得非边界顶点2需要添加的驱动为 3-3=0，其中第一个“3”为C1中第2行的元素和。此时的邻接矩阵C2为

同时变量由D1变为D2,则D2=D1+0=1。

然后继续对非边界顶点3添加驱动，由式(1)和邻接矩阵C2得非边界顶点3需要添加的驱动为 2-3<0，其中的“2”为C2中第3行的元素和(若存在非边界顶点行元素和小于或等于3，则需要添加的驱动为0)。此时的邻接矩阵C3为

同时变量由D2变为D3,则D3=D2+0=1。

由上述计算可得非边界顶点1、2、3需要的总驱动数量Me=D3=1。

下面计算边界顶点所需要的驱动数，边界顶点需要的总驱动数Mb计算如下：

(3)

其中，b为非分边界顶点数，n为图形的总顶点数，rb(j)为最后一个非边界顶点添加驱动后的邻接矩阵中的第j行的和。

由邻接矩阵C3和式(3)可以得到多顶点三角形刚行折纸图案边界顶点需要添加的总驱动数为

可以发现邻接矩阵C3中第4行至第9行每一行的和都是2，则由式(7)可得边界顶点需要的约束为Mb= 0。最后，计算得到多顶点三角形刚性折纸机构的自由度:M=Me+Mb=1。

4 模拟仿真

通过Adams软件的建模仿真功能，建立多顶点三角形刚性折纸图案，建模过程中，刚性折纸的折痕视为旋转关节(细线表示)，刚性纸板则视为连杆。连杆与连杆之间由旋转副连接，通过约束的方式使连杆与连杆仅存在转动自由度。多顶点三角形刚性折纸图案的三维建模图形如图6所示。

在完成建模的基础上，为模型添加驱动，模型的驱动添加数为上述计算结果，模型仅需添加一个驱动。然后，执行仿真运行步骤，看能否完成刚性折叠过程。

多顶点三角形刚折纸运动模型完成了从初始平折到完全折叠的运动过程，结果如图7所示，机构仅添加一个驱动即可完成所需的折叠运动(驱动添加图如图8所示)，运动过程并无奇异位形，若添加多个驱动则可能会产生冗余驱动。仿真结果验证了多顶点三角形刚性折纸的自由度为1的结论是正确的。

图7 多顶点三角形刚性折纸图案的运动完成折叠

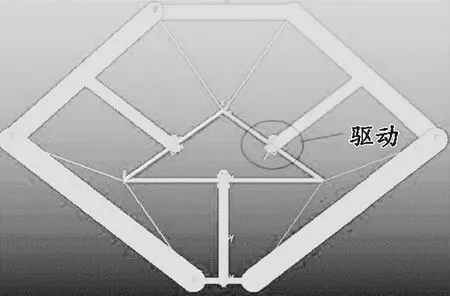
图8 多顶点三角形刚性折纸图案的折叠驱动添加

5 结束语

在刚性折纸的平折条件和峰谷分配的条件等条件下，以分析单顶点4折痕的刚性折纸自由度为基础，拓扑到多顶点三角形刚性折纸自由度分析，通过邻接矩阵的方法分析多顶点三角形刚性折纸的自由度，该方法具有运算简单、表达直观的优点。顶点之间的关系用邻接矩阵表示，便于计算机运算和矩阵变换。通过引入消元矩阵，用矩阵乘法描述了确定运动状态的过程，通过矩阵变换简化了折纸图案中的复杂运动表示。最后通过软件仿真验算其计算结果的准确性。