国家数值风洞(NNW)工程在高超声速中的应用研究进展
2021-10-20陈琦陈坚强袁先旭郭启龙万钊邱波李辰张毅锋
陈琦,陈坚强,袁先旭,郭启龙,万钊,邱波,李辰,张毅锋,*
1. 中国空气动力研究与发展中心 空气动力学国家重点实验室, 绵阳 621000
2. 中国空气动力研究与发展中心 计算空气动力研究所, 绵阳 621000
长期以来,中国CFD软件市场基本被国际商业软件垄断,国产CFD软件在体系化、工程化以及市场化等方面与欧美国家存在较大差距。为此,中国在2018年启动了国家数值风洞(NNW)工程,通过自主发展算法模型、研发系列CFD软件、建设高性能计算机系统,形成自主知识产权、国内开放共享的空气动力数值模拟平台,满足中国航空航天等领域对自主CFD软件产品的需求[1]。
为使国内CFD从业人员了解国家数值风洞工程,促进NNW系列软件在全国各领域的推广和应用,本文以高超声速流动为例,选取了复杂流动特征高保真模拟、复杂干扰机制高清晰认知以及多学科耦合应用3个专题,从不同角度展示NNW系列软件的应用效果和功能特点。其中,复杂流动特征专题包含微型涡流发生器在激波边界层干扰中的应用,一种雷诺平均/大涡模拟 (Reynolds-Averaged Navier-Stockes equations/Large Eddy Simulation, RANS/LES)混合模型在圆柱底部绕流中的应用,可压缩解析壁面函数在热流高效预测中的应用,以及采用直接数值模拟(DNS)在圆锥边界层Mack模态的线性和非线性演化过程中的应用等4部分内容。复杂干扰机制方面,揭示了钝舵缝隙内部涡串干扰机制,分析了吸气式飞行器进气道唇口激波振荡高低频转化过程,研究了喷流诱导回流激波产生底部高温区的现象。在多学科耦合应用方面,研究了舵面操纵下导弹的动态响应特性,计算了气动伺服弹性效应对导弹控制系统的影响,分析了化学非平衡效应对动态稳定性的影响规律。
1 复杂流动特征高保真模拟
1.1 激波-边界层干扰精细模拟
激波-边界层干扰是激波与边界层相互作用的一种典型的非线性、非定常、黏性主导的复杂流动,是一种普遍存在于高超声速飞行器的流动现象。由于它可能会带来总压降低、流动非定常振荡、局部高热流等负面效应,因此对飞行器的气动特性和飞行安全有重要的影响,是高速飞行器设计中必须考虑的关键问题。在数值模拟时,由于流场中同时存在激波与多尺度湍流边界层,故要求所采用的数值方法在结构分辨能力和计算稳定性之间达到平衡。激波-边界层干扰问题的直接数值模拟,主要应用了NNW工程发展和集成的高精度WENN/WENO系列算法[1-3]、激波识别技术[4-5]和湍流入口生成技术[6-7]。
图1给出了计算域内(图中X、Y、Z分别表示3个方向空间无量纲坐标)超声速压缩拐角的瞬时旋涡结构,用流向速度着色,Q=0.01。可以看出,在干扰前后流场中旋涡分布与尺度存在差异:在干扰区前旋涡结构的尺度要比之后的略小,并且更靠近边界层外层,经过激波后,湍流强度变强,边界层变厚。图2给出了物面压力分布与实验数据的比较,其中X为流向坐标,δ为入口边界层厚度,Pw表示壁面压力,Pinf表示以来流速度和密度计算的参考压力,计算得到的压力分布与实验值整体符合较好。图2 中,在拐角处出现了一个压力拐点,在拐点前压力的增长速度变小,这是分离区的位置。

图2 物面压力分布与实验对比Fig.2 Pressure distribution on wall contrast to experiment data
在高超声速的激波-边界层干扰方面也进行了直接数值模拟,获得了精细的旋涡结构和低频非定常运动过程;并且还对微型涡流发生器(MVG)在激波边界层干扰中的应用开展了研究,图3给出了其平均及瞬时密度分布。计算采用Duan等[9]的高超声速边界层DNS来流条件:来流马赫数Ma∞=5.0,雷诺数Reθin=2 300,来流温度T∞=228 K,壁面温度Tw=433 K。网格及边界的详细设置参见文献[10,11]。图中:MW表示马赫波,结构“S1”和“S2”分别表示前缘激波和后缘激波,分区“I”和“II”分别表示近稳态区和间歇性大尺度涡流区。

图3 平均及瞬时密度分布Fig.3 Average and instantaneous density contours
研究发现,微型涡流发生器能够有效减小分离区长度,并且对于干扰区后的热流也有显著的调制作用。进一步研究微型涡流发生器后速度和湍流脉动剖面的自相似特性,发现与超声速情况类似,高超声速条件下微型涡流发生器后的速度和湍流脉动剖面存在自相似性,并且给出了自相似律,如图4和图5所示[11],其中散点为不同流向位置的实验数据,U、V表示流向和法向的平均速度,u′、v′分别表示流向和法向脉动速度的均方根,u′v′表示雷诺切应力,各个物理量的下标“scale”表示对其进行相似变换,具体的变换公式参见文献[11]。

图4 归一化的流向和法向速度分布[11]Fig.4 Distribution of scaled streamwise and normal velocity[11]
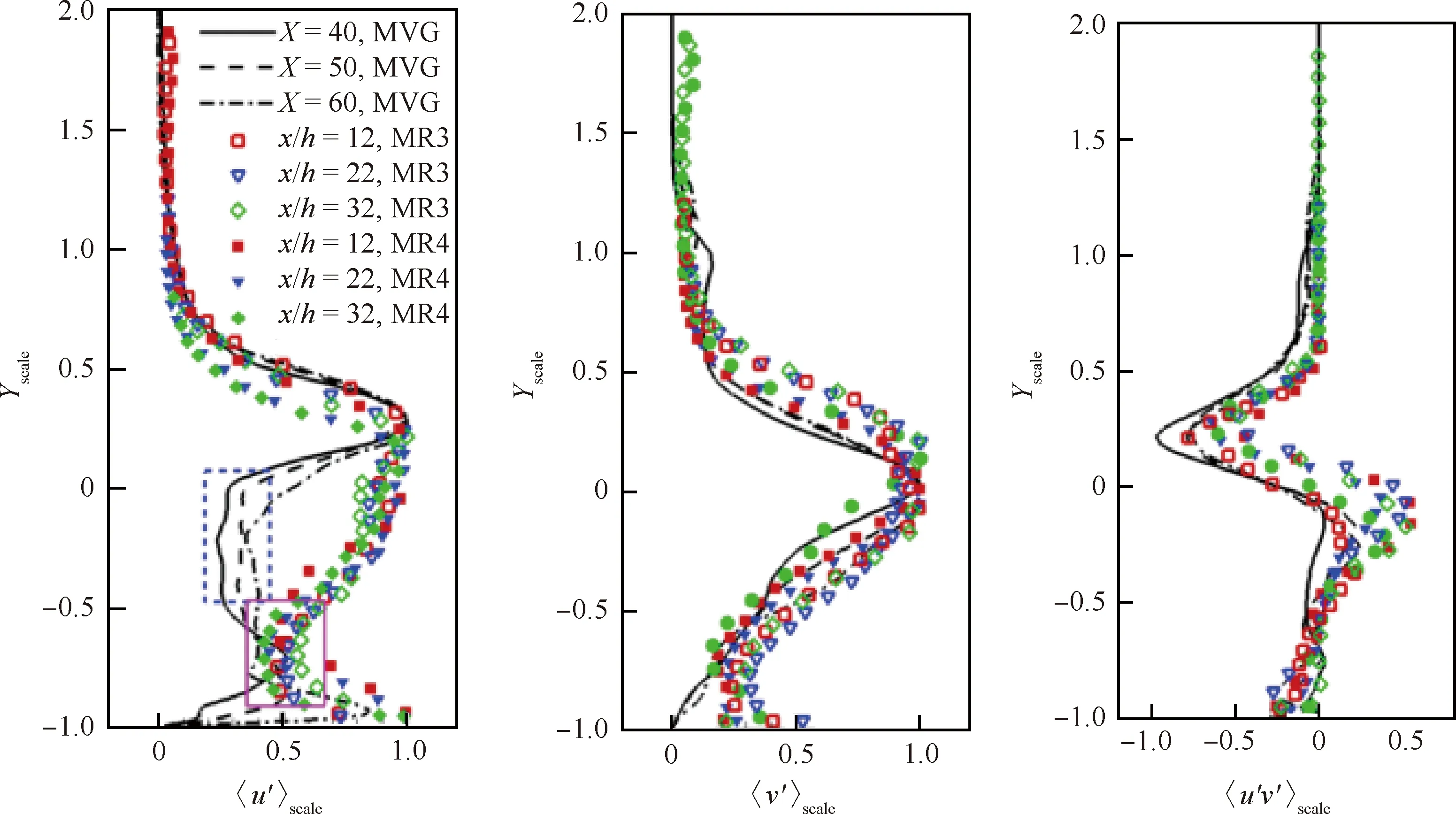
图5 归一化的u′v′u′v′分布[11]Fig.5 Distribution of scaled turbulent quantities u′v′u′v′[11]
1.2 湍流高精度模拟
Prandtl的混合长度模型与Smagorinsky亚格子模型十分相似,通过过渡函数将两种模型组合起来是比较好的构造脱体涡模拟(DES)的方式,已经有学者做过类似的工作,并取得了较好的效果[12]。孙东等深入分析了亚格子应力的组成以及彼此之间的关系后,结合现有的算法发展出了ML-DES算法[13-14]。袁先旭等在文献[14]提出的混合模型的基础上,引入壁面和网格拉伸比的影响,对亚格子尺度和过渡函数进行了修正;同时针对传统模型采用突然变换的判断函数,导致过渡不连续的问题,在Fujiik[15]提出的过渡函数基础上,基于不可压湍流边界层特性,研究提出了一种新型过渡函数,形成了一种新的RANS-LES混合模型,具体可参考文献[12]。
在RANS-LES混合模拟中,整体预测精度主要取决于LES部分的精度[16-18]。而LES对于计算格式、计算网格都有着较高的要求,如何正确配置计算格式和网格对于误差控制具有重要的意义。邓小兵[19]系统开展了LES计算中非线性多尺度系统的数值误差分析,为数值格式的设计以及网格分布提出了指导原则。研究发现,显式滤波能够准确定义滤波可分辨尺度和亚滤波尺度,避免了网格尺度大小的空间离散误差对大尺度运动的污染,能够实现对数值误差的有效控制;并且通过对计算过程中混淆误差、色散误差以及耗散误差的分析(图6[19]),发展了适用于RANS-LES计算的高精度格式构造方法。图6中给出了使用多种高精度格式开展均匀各向同性湍流LES计算时所表现出的混淆差、色散误差和耗散误差影响,其中k表示空间波数,Δ表示网格尺度,E(k)为湍动能能谱,“CBCexp”为不同时刻实验测得的能谱数据,“optC4”表示邓小兵提出的一种4阶中心型格式[19],“Spectral-like”表示经过谱特性优化的中心型紧致格式(截断波数为ωc),“E2”和“E4”分别表示2阶和4阶中心差分格式,“Up3”和“Up5”分别表示3阶和5阶迎风偏置格式。
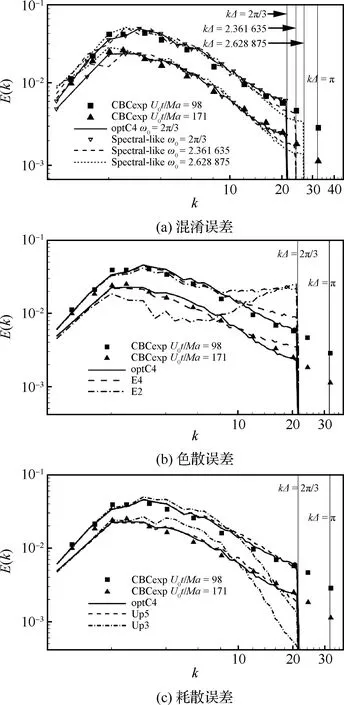
图6 混淆误差、色散误差和耗散误差对均匀各向同性湍流LES计算结果的影响[19]Fig.6 Influence of aliasing error, dispersion error and dissipation error on LES result of homogeneous isotropic turbulence[19]
使用超声速圆柱底部流动问题对比了基于Spalart-Allmaras(SA)模型的模拟方法和基于RANS/LES混合模型模拟方法的计算结果。自由来流Ma∞=2.46,单位雷诺数Re/L=45×106/m,T∞=145 K,P∞=31 415 Pa。圆柱半径R=31.75 mm,圆柱长为8R,计算网格规模约1 000万。图7(a)给出了SA模型和混合RANS/LES模拟得到的瞬时密度梯度分布云图,可以看到混合RANS/LES计算结果清晰地呈现出充分发展的湍流脉动结构。图7(b)给出了用压力着色的底部涡量等值面云图(压力用来流动压进行无量纲压化)。可以看出,混合RANS/LES模型捕捉到了底部区域的主要流动结构,而SA模型仅能给出平均量。

图7 超声速圆柱底部绕流流动结构Fig.7 Flow structure around bottom of a supersonic cylinder
图8为圆柱底部压力系数Cp和速度U不同方法下的分布情况,其中r和x分别为尾迹区径向坐标和流向坐标,U为流向平均速度,参考的实验数据来自文献[20]。相比于SA模型计算结果,混合RANS/LES模型得到的计算结果与实验值更加接近。

图8 RANS/LES混合模型与实验和SA模型结果对比Fig.8 Comparison of results of RANS/LES method,experiment and SA model
1.3 热流高效高精度模拟
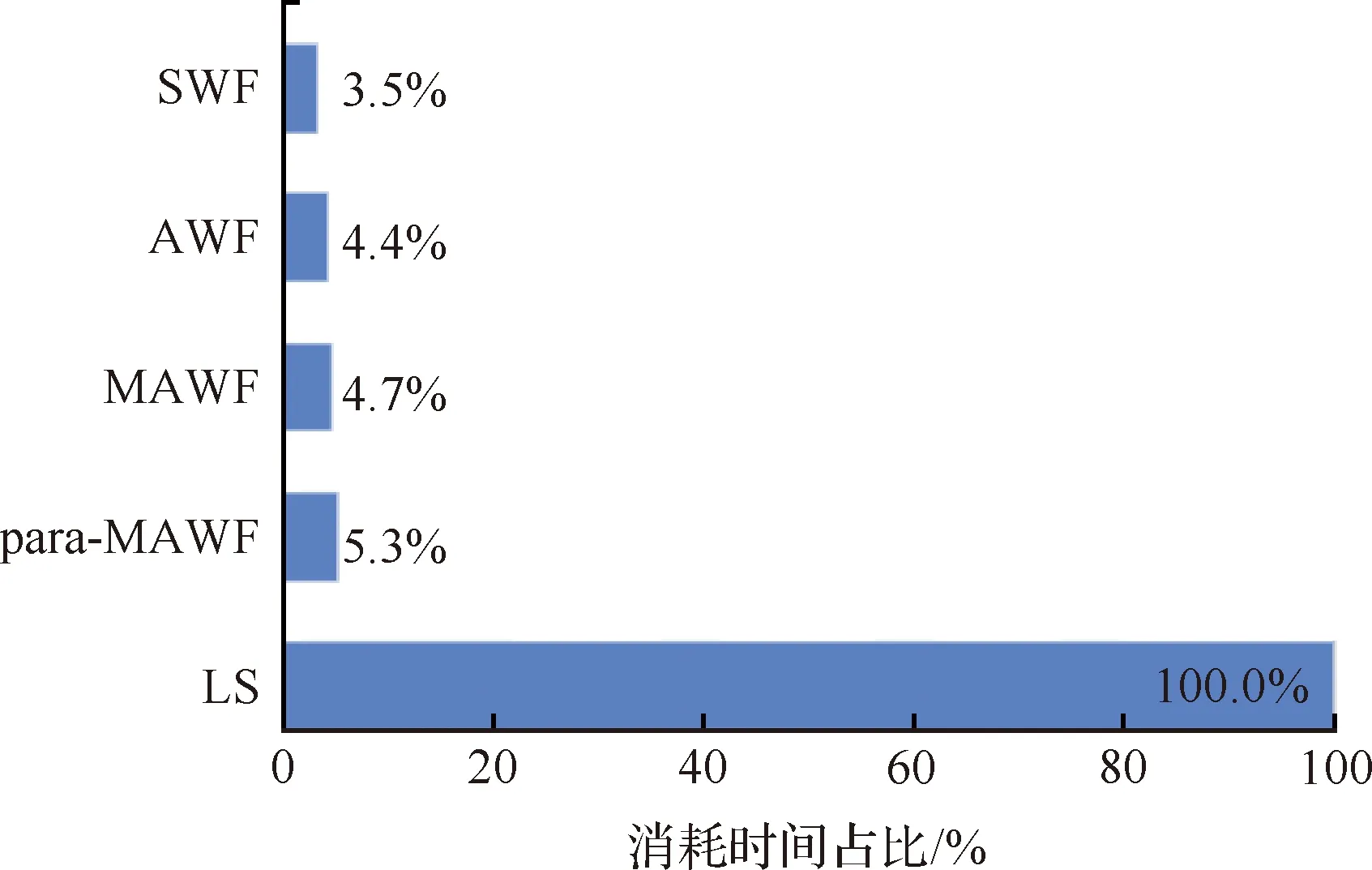
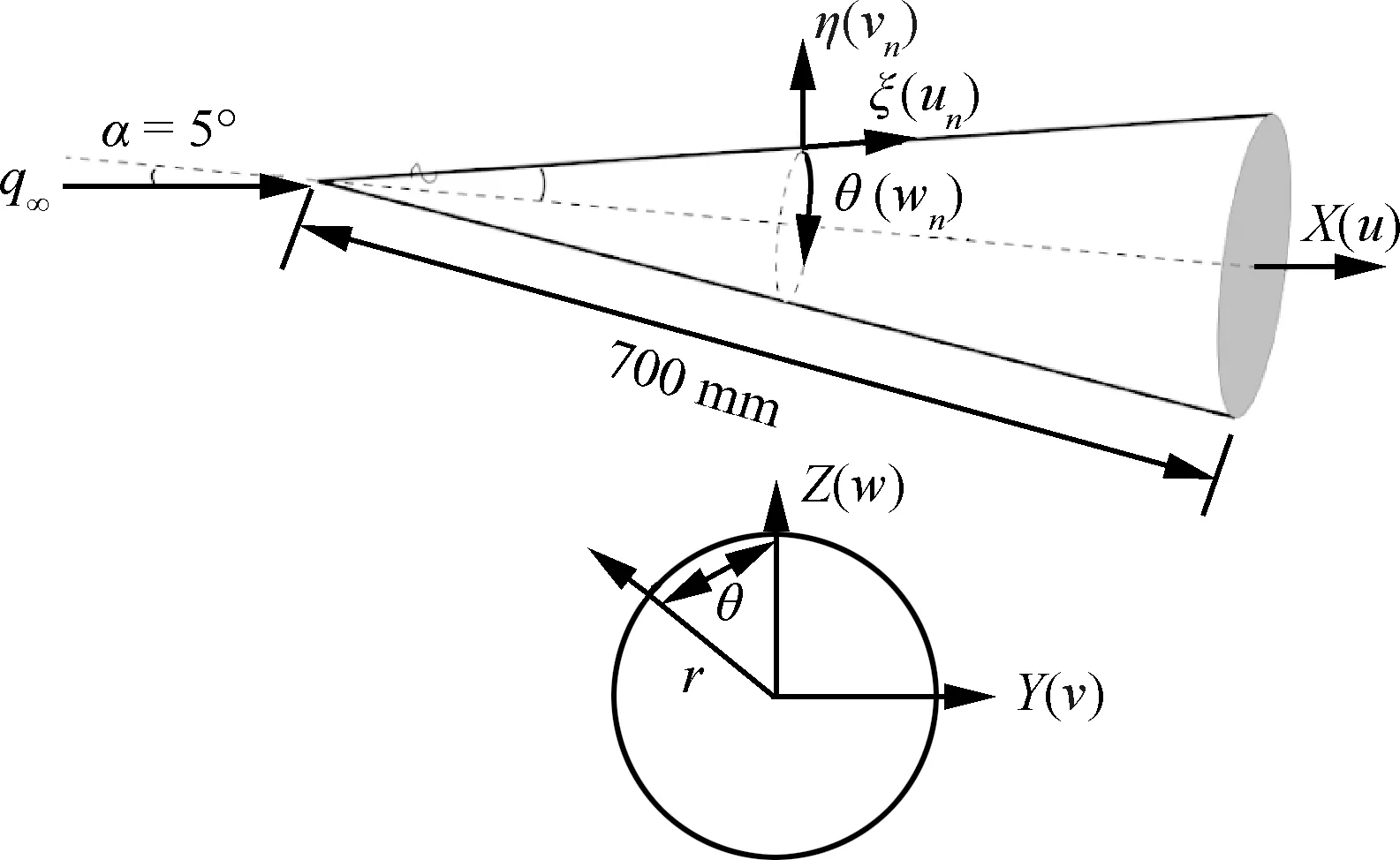
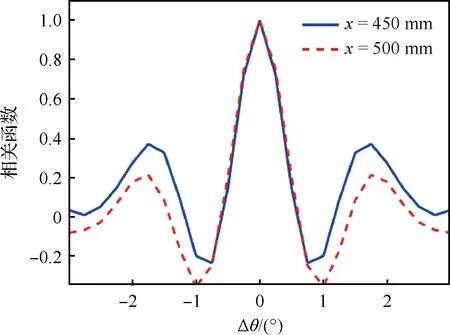
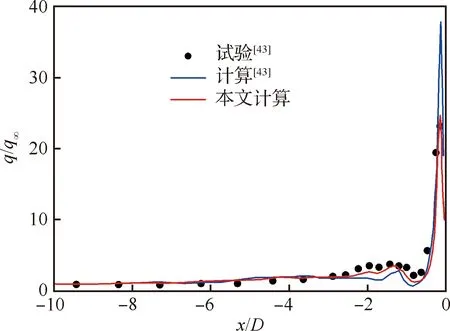
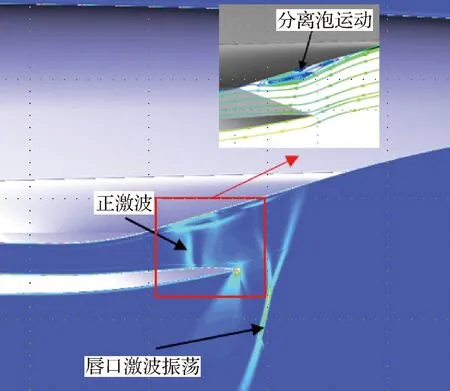
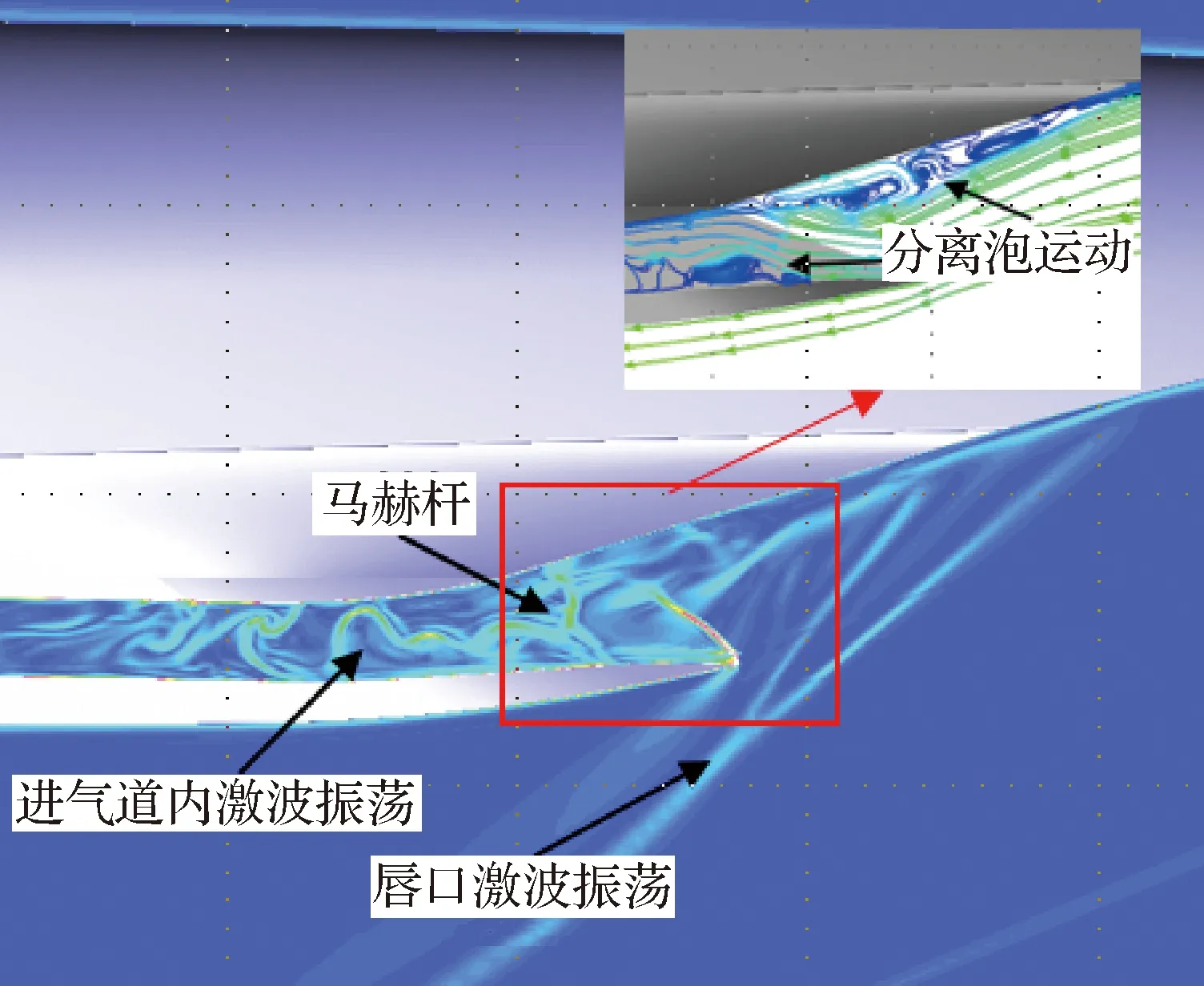
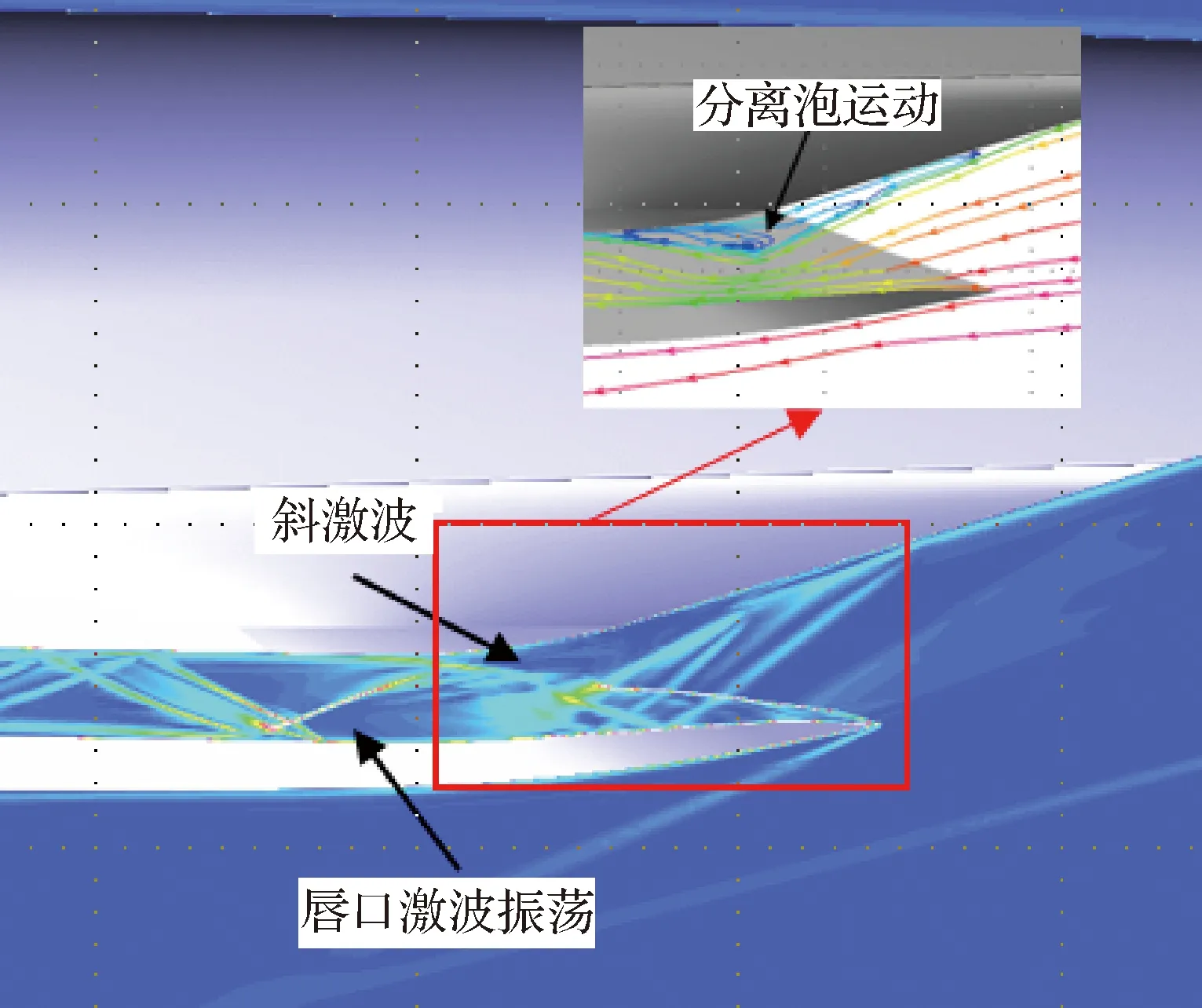
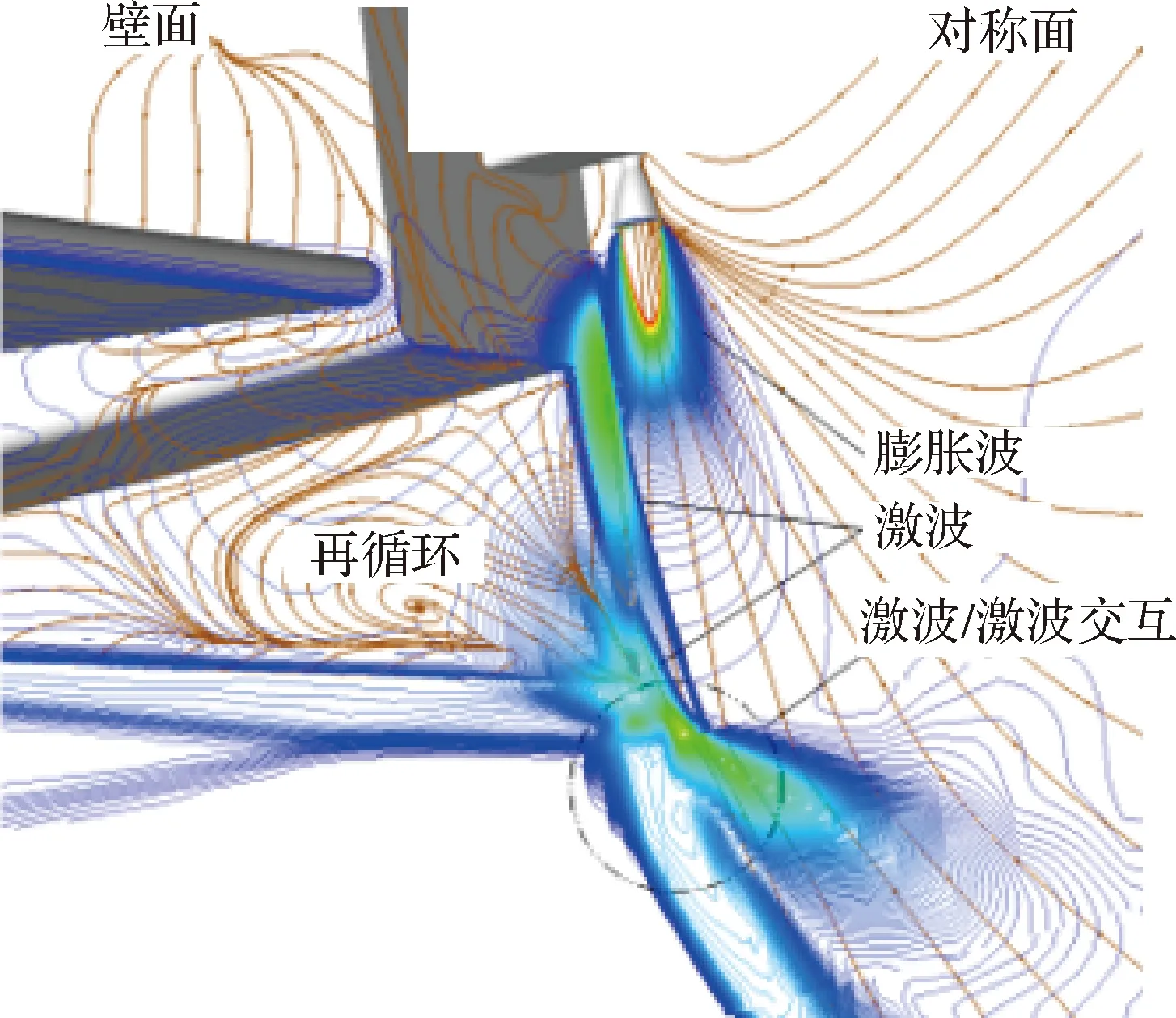
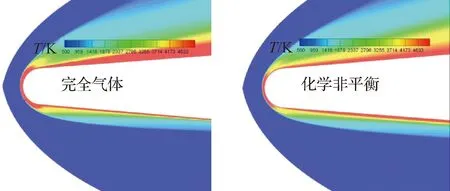
高超声速飞行器湍流数值模拟通常使用RANS方法,需要向壁面网格加密(y+≈1),带来计算收敛慢、计算稳定性下降等问题。因此,主流商业软件,例如Fluent和CFD++等,对工程外形进行湍流模拟时通常使用壁面函数(通常20 文献[21]总结了近50年壁面函数的发展,其中对于可压缩流动,在标准壁面函数的基础上,通过添加压力梯度[22]、可压缩性和壁面传热效应[23]等修正,扩展了壁面函数的应用范围,但对于存在分离和再附等逆压梯度的复杂流动,其适用性仍无法确定[24]。 文献[25]发展的解析壁面函数通过在壁面附近解析求解简化的湍流边界层方程,得到速度和温度的解析表达式,在低速分离流动中表现良好。文献[26]基于可压缩湍流边界层的特征,在简化方程中添加了对流项分布和能量方程中黏性耗散项的影响,发展了一种适用于可压缩流动的解析壁面函数,可有效消除原始解析壁面函数在激波边界层干扰算例数值模拟中出现的非物理振荡和壁面热流预测精度差等问题,接近密网格低雷诺数模型预测结果。 图9比较了不同来流马赫数时的可压缩湍流边界层[27-29]内的温度分布,图中Ma=5的实验结果来自文献[28],Ma=8.2的实验值来自于文献[29],LS model表示采用Launder-Sharma模型的计算结果,T表示温度,Tw表示壁面温度,T∞表示来流温度,δ表示边界层厚度,y表示壁面距离。通过图9可以看出,随着马赫数的增加,壁面边界层内温度变化加快,导致流体层流黏性系数等参数变化。为此,发展了高超声速湍流边界层解析壁面函数方法,并集成到NNW软件中,为工程上快速精确的湍流模拟提供了一种思路。 图9 可压缩湍流边界层近壁面温度分布Fig.9 Near-wall temperature distribution in turbulence compressible boundary layer 解析壁面函数在壁面附近通过可压缩湍流边界层假设简化输运方程,考虑对流项和压力梯度的影响,其中对流项在壁面网格内变化较大,因此基于壁面网格点的对流项可使用无量纲壁面距离的平方项进行模拟,同时可压缩湍流边界层内能量方程黏性耗散项不能忽略。 通过给定湍流黏性系数分布,进行两次积分可得到壁面速度和温度表达式,进而得到可压缩流动的解析壁面函数(MAWF)。结合解析壁面函数的构造过程和层流黏性系数分布规律,在黏性底层内构造一种抛物型(Parabolic)分布: (1) 图10比较了马赫数Ma=8.2算例分离区前后壁面网格内层流黏性系数分布,其中密网格数值结果(LS)表明黏性系数在底层内变化较大,约30%,而本文构造的层流黏性系数相较于MAWF在壁面网格内使用壁面值,接近于密网格结果,合理地描述了强可压缩流动中黏性底层内的变化。通过相似的积分过程,可以得到考虑层流黏性系数变化的解析壁面函数,即para-MAWF。 图10 黏性系数分布(Ma=8.2)Fig.10 Distribution of viscosity variation (Ma=8.2) 斜激波边界层干扰会产生激波反射、分离和再附等复杂流动现象,是考核壁面函数常用的算例,这里选取Ma=5.0和Ma=8.2两个状态进行比较。Ma=5.0算例的来流条件和网格等可参考文献[26]。Ma=8.2算例[29]来流压力为430 N/m2,来流温度为81 K,壁面温度为300 K,计算网格中包含激波产生器(β=10°)来模拟入射激波。计算中所有网格均经过网格无关性测试,最终低雷诺数湍流模型使用的密网格为480×105,分离区前y+≈0.6,壁面函数使用的粗网格为160×60,分离区前y+≈30。计算网格和模型尺寸如图11所示。 图11 Ma=8.2激波边界层算例网格示意图Fig.11 Sketch map of mesh for Ma=8.2 shock wave boundary layer calculation example 图12比较了Ma=5激波产生器10°的Stanton数St分布,横坐标中x1表示斜激波无黏反射位置,其中EXP为实验数据[28],AWF、SWF和MAWF分别表示原始解析壁面函数、标准壁面函数以及添加可压缩修正的解析壁面函数的计算结果,para-MAWF为本文添加黏性底层层流黏性系数分布后的解析壁面函数数值预测结果,LS表示低雷诺数模型Launder-Sharmak-ε模型计算结果。AWF结果在分离起始位置出现非物理振荡,主要原因是AWF对流项在壁面网格内的分布,将导致AWF预测能力降低。而MAWF认为对流项在壁面处为零,以无量纲壁面距离的平方项递增,从物理上更符合边界层内流动规律,从而提高预测精度。MAWF相较于AWF,壁面热流的预测能力大幅上升,主要得益于能量方程简化中保留了黏性耗散项,使得粗网格预测的壁面热流精度大幅改善,接近密网格LS的结果。SWF在分离区前后均无法准确预测壁面热流。添加层流黏性系数变化的解析壁面函数,对于本算例影响较小,接近于MAWF结果。图13比较了不同湍流模拟方案消耗的时间对比,其中解析壁面函数消耗的时间仅为密网格LS的5%左右。 图12 Ma=5.0算例壁面Stanton数分布Fig.12 Stanton number distribution for Ma=5.0 图13 Ma=5.0耗费计算机时间对比Fig.13 Comparison of CPU time for Ma=5.0 图14比较了Ma=8.2算例激波产生器10°的壁面热流Q/Q∞结果,其中EXP-SB和EXP-TC均来自实验数据[28],分别表示使用塞式热流传感器(SB:Schmidt-Boelter gage)和热电偶(TC:thermocouples)测量的壁面热流,LS表示低雷诺数模型Launder-Sharmak-ε模型计算的结果,MAWF为文献[26]发展的解析壁面函数计算结果,para-MAWF为本文添加黏性底层层流黏性系数分布后的解析壁面函数数值预测结果,从图中可知相较于MAWF,考虑层流黏性系数分布的解析壁面函数得到壁面热流在分离区显著降低,更接近于实验值,相较于密网格LS模型降低了约30%。密网格LS结果严重高度壁面热流,和文献[30]中密网格低雷诺数模型结论一致,均出现高估高超声速算例壁面热流现象。 图14 Ma=8.2算例壁面热流分布Fig.14 Heat-flux distribution on wall for Ma=8.2 在过去的20多年里,亚利桑那大学的Fasel课题组采用直接数值模拟方法对0°攻角锥表面第二模态的自然转捩过程开展了大量的研究[31-35],他们发现在第二模态的非线性阶段会出现流向条带。而在横流效应下(虽然在迎风对称面附近的横流速度较小),迎风中心线附近第二模态的自然转捩与0°攻角钝锥表面存在何种异同是值得研究的课题。因此,本文采用直接数值模拟,研究了飞行工况下迎风中心线上最不稳定Mack模态的线性和非线性演化过程,并将其与0°攻角圆锥边界层中Mack模态的自然转捩过程做了对比。 如图15所示,研究对象为一个半锥角7°、头部半径5 mm、长度700 mm的钝锥。来流条件为飞行工况:马赫数Ma∞=6、单位长度雷诺数Re∞=2.079×107/m、温度T∞=216 K、攻角α=5°。壁温Tw=500 K。直角坐标系(X,Y,Z)和贴体坐标系(ξ,η,θ)中的速度分量分别为(u,v,w)和(un,vn,wn),周向角θ在背风和迎风对称面分别为0°和180°。 图15 坐标系和模型示意图Fig.15 Sketch of coordinates and computational model 数值模拟主要分为4步: 第1步采用二阶精度的有限体积方法获得包含头部和激波的基本流,网格尺寸为Nξ×Nη×Nζ=1 000(流向)×401(法向)×181(周向)。第1层网格离壁面的距离从驻点的4×10-3mm线性增长到计算域出口的8×10-3mm。 第2步为减少网格与激波不平行带来的数值振荡,利用第1步的流场获得激波位置,生成与激波平行的网格,并采用和第1步相同的格式和网格量重新计算层流场。在前两步中,考虑到流动的对称性,计算仅使用半模。 第3步截取一个不包含激波和头部的子计算域,采用高阶有限差分获得密网格下收敛的层流解,网格大小为Nξ×Nη×Nζ= 8 000×240×380。子计算域的入口位于x=150 mm处,在该流向位置,背风和迎风对称面上远场离壁面的距离分别为当地边界层厚度的2.5倍和8倍。入口、远场边界条件以及初始场从上一步中插值得到。由于关心的是迎风面扰动的演化过程,为减少计算量,整个背风面为周向缓冲区,周向网格从侧方对称面向背风对称面逐渐稀疏,周向缓冲区网格点总数为60,因此,在迎风面,网格点的周向间距为1°,同样,流向也设置缓冲区(约300 mm),网格量为100。在周向也采用了类似的网格分布[36]。法向网格采用指数拉伸,在每个扇面(k=1, 2,…,Nζ),网格点离壁面的法向距离满足: (2) 式中:Lη(i,k)是当地远场到壁面的法向距离;i=1, 2,…,Nξ;j=1, 2,…,Nη;参数b通过第1层网格离壁面的距离η(i, 2)=2.5×10-3mm来确定。边界层内网格点约为120~130。 第4步在第3步的层流场中施加非定常壁面吹吸。吹吸形式为 vbs=Asin((x-x1)/(x2-x1))3rand(z,t) (3) 式中:vbs为沿物面法向的速度;x1和x2为吹吸槽在流向的边界,吹吸幅值A为来流速度的10-3。图16为线性稳定性得到的不同频率Mack模态的N值(增长率沿流向的积分)沿流向的变化。频率f=1.5 MHz的Mack模态达到的N值最大,其中性点在x=300 mm附近,因此,将吹吸频率设为1.5 MHz,吹吸槽位于x1=280 mm和x2=282 mm之间。 图17为迎风面附近的时均摩阻系数Cf,很明显在模型的下游出现了条带,这与0°攻角锥在风洞工况下的结果是类似的,这表明,虽然有攻角时边界层是三维的,但是第二模态的失稳形式与二维高超声速边界层是类似的,即都是基频共振(Fundamental Resonance)。 图16 线性稳定性理论得到不同频率Mack模态N值沿流向的变化Fig.16 Variation of N-factors of Mack modes at different frequencies in streamwise direction by linear stability theory 图17 迎风面附近的时均摩阻Fig.17 Temporal-averaged skin friction around windward plane 图18为x=450 mm和500 mm处时均摩阻在周向的相关函数,横坐标为周向角度的间隔。结果表明条带之间的间距约为2°, 按弧长计算约为边界层厚度的2~3倍。这比飞行工况下二维湍流边界层中第二模态转捩引起的条带之间的间距要小,虽然在不同工况下条带之间的绝对距离没有可比性。 图18 x=450和500 mm处时均摩阻周向的相关函数Fig.18 Azithumal correlation function of temporal- averaged skin friction at x=450,500 mm 图19为转捩前期温度的典型均方根及其频谱,图19(a)给出了x=400 mm处温度的时均值(虚线)和均方根(云图),其中纵坐标η表示距物面的距离,横坐标为周向角;图19(b)针对图19(a) 中的3个采样点“△□○”,给出了采样点处的温度脉动频谱。结果表明,温度均方根在近壁面和边界层附近存在两个极值,这表明转捩确实是由第二模态失稳引起的。从图19(b)还可以看出,第二模态的频率约为1.6 MHz,这与图16中稳定性分析得到的结果吻合。 图19 x=400 mm处温度的均方根及其频谱分布Fig.19 Distribution of RMS and spectra of temperature at x=400 mm 高超声速飞行器在穿过大气层时会面临严酷的气动加热[37-38],钝舵作为高超声速飞行器典型的凸出部件,外部的高气流绕过钝舵时,会在钝舵前产生激波。而激波打到飞行器物面上会发生激波-边界层干扰,同时钝舵与机体交汇处通常会发生分离与再附,进而形成一系列局部高热流区。为了完成变舵偏等飞行动作,钝舵底部往往会留有一定的缝隙结构,缝隙的存在会使得钝舵结构变得更加复杂[39-40],复杂的流动结构对于钝舵缝隙的数值模拟提出了较大的挑战。与此同时,由于钝舵前缘、舵轴及安装面常常是烧蚀的“重灾区”,整个钝舵缝隙结构是热防护设计的重点。 高超声速钝舵缝隙数值模拟有两个难点,一是缝隙尺寸和飞行器尺寸之间相差巨大,这对网格的生成提出了很高的要求;二是缝隙内的黏性流动和缝隙外的高超主流在流动速度上相差巨大,这对计算格式提出了很高要求。在计算网格方面,需要根据丰富的热环境网格绘制经验,绘制过渡充分均匀光滑,近壁面正交性和尺度良好,空间无“边界层”密度的结构网格。在计算格式方面为了能在捕捉激波的同时,很好地模拟缝隙的低速黏性流动,采用了Van Leer[41]加焓守恒修正格式。Van Leer分裂具有很好的激波捕捉能力,但它的缺点是在边界层、剪切层计算中格式耗散过大,降低了黏性流动模拟精度。因此,在Van Leer通量分裂的基础上引入了焓守恒修正[42],减小了边界层、剪切层中的格式耗散。有效抑制了非物理耗散,在一定程度上解决了流场分辨率与计算稳定性之间的矛盾。 选用李艳丽和李素循[43]的无缝隙钝舵作为计算模型,模型结构如图20所示,详细尺寸和来流参数见文献[43]。 图20 钝舵模型[43]Fig.20 Geometry of blunt rudder[43] 图21给出了钝舵计算流场结构与试验流场结构的示意图,图22给出了钝舵前缘中心线平板热流对比图,纵坐标为无量纲化的热流,其中参考热流qref为相同来流条件下,没有钝舵干扰时对应钝舵位置的平板热流值,横坐标为以舵轴前缘为零点,用钝舵前缘直径进行无量纲化的平板中心线位置无量纲值。从图21、图22可以看出计算结果无论从流场结构还是表面热流均与文献[43]的试验结果较好吻合,这在一定程度上验证了计算结果的可靠性。 图21 钝舵流场结构对比Fig.21 Comparison of flow structure around blunt rudder 图22 钝舵前缘平板热流对比Fig.22 Comparison of heat flux at leading edge of blunt rudder 为更好符合实际飞行器钝舵情况,基于无缝隙钝舵,建立带缝隙钝舵简化模型,舵轴直径12 mm 位于舵正中,舵缝隙高4 mm。网格第1层高度取0.001 mm,网格法向增占比控制在1.1以内。图23给出了钝舵缝隙对称面马赫数云图和二维流线分布。从图中可以看到,绕钝舵流动,舵前缘形成脱体激波。平板边界层发生分离形成的分离激波与脱体激波碰撞形成复杂的波系结构,舵根部上游区域出现了马蹄涡结构,如图23(a) 所示。其次,钝舵前缘流体填充至缝隙内部,从马赫数云图可以看出,缝隙内部流体速度迅速降低,变为低速的黏性流体。由于分离再附的作用,低速黏性流体在缝隙的上底面和下底面形成了多个旋涡结构,如图23(b)所示。 图23 对称面马赫数和流线分布Fig.23 Distribution of Mach number and stream line on symmetric plane 为了更好观察发现流场结构,分析流动特性,从钝舵缝隙模型前缘到后缘,以舵轴为对称面截取了7个垂直截面,沿着流动方向依次为P1~P7截面,将缝隙上下物面热流与7个缝隙截面二维流线进行对照比较,如图24、图25所示。对于舵轴上游截面,各截面内均出现了涡串结构。从P1截面开始出现四涡结构,到达舵轴上游缝隙中部位置附近(P2截面),涡的数量多达6个,相应缝隙上下物面再附区域横向有明显的马蹄形高热流区,这主要是由于来流受舵缝和舵轴的影响,在上下表面多次出现分离再附引起的。从P2~P3截面可以看出,缝隙底部旋涡向舵面两侧发展,并很快发展到两侧的舵面上,并在舵侧面形成了一条高热流带。从P4截面来看,受舵轴的影响,缝隙内旋涡结构在舵轴处基本消失。对于舵轴下游缝隙区域,P5、P6和P7截面缝隙内部流线较为简单,物面没有热流高值区,舵轴后缘由于是背风区,因而出现了热流低值区。缝隙外部马蹄涡沿着舵面不断向上抬升,到钝舵的后缘附近(P7截面),旋涡结构发展到最大,其影响范围也最远,同时受旋涡运动的影响,缝隙上底面侧棱附近出现了一条明显的高热流带。总的来看,流场结构清晰合理、壁面热流光滑连续,流场结构基本可以解释壁面热流分布规律,计算结果具有较高可信度。 图24 下表面不同站位附近热流和流线分布Fig.24 Heat flux and stream line at different cross section on lower surface 图25 上表面不同站位附近热流和流线分布Fig.25 Heat flux and stream line at different cross section on upper surface 吸气式高超声速飞行器进气道经常面临激波/边界层、激波/激波相互作用等[44],使得进气道唇口产生非定常的激波振荡,而进气道内激波串的相互作用也可能产生自激振荡的现象[45-46],严重时会使得进气道壅塞并导致发动机不启动现象[47-50],需要加以控制[51-52]。目前进气道大都采用前体/进气道一体化设计以得到更好的发动机推力性能和飞行性能[12]。有必要对整机采用内外流一体化计算,考察不同来流工况下,进气道激波振荡机制以及飞行器整体气动力特性的变化,支撑进气道的优化设计。 为了模拟飞行器在不同工况下的进气道激波振荡过程,基于NNW通用软件,开发了内外流一体化RANS-LES混合模拟方法,提高了对进气道分离流动及复杂波系感染的分辨能力。 计算模型采用了某工程升力体外形,计算状态为:高度20 km,来流温度为216.65 K,攻角和侧滑角均为0°;为了研究来流速度对进气道波系结构的影响,设置4种来流马赫数:Ma=1.5, 3.0, 5.0,7.0。计算网格在进气道和壁面处进行了加密,网格规模2 000万。 吸气式飞行器进气道的流动受到多种因素的影响,比如来流速度、飞行高度、飞行攻角等。本节通过设置不同的来流马赫数,研究来流速度对进气道激波振荡过程的影响。图26给出了来流Ma=1.5的流动结构,主图为密度梯度分布云图,并给出了红色方框内的流线分布图。可以看到,当飞行马赫数较低时,进气道上压缩面边界层发生流动分离,并产生大尺度的分离泡;分离泡周期性地变大或缩小并产生低频振荡;继而与斜激波相互作用,使得斜激波在唇口来回运动并同样产生低频振荡。在进气道入口附近产生一道正激波,正激波后压力较高,使得进气道壅塞。飞行器的气动力整体上也呈现出低频振荡特征。 图26 Ma=1.5流动结构Fig.26 Flowfield structures at Ma=1.5 当飞行马赫数增大至3.0时,如图27所示,分离泡结构发生显著变化,在进气道上、下压缩面均产生了分离泡,部分斜激波打入进气道内部。在进气道入口附近产生马赫杆结构,来流只能从马赫杆两侧进入进气道,使得进气道部分壅塞。唇口激波低频振荡,进气道内激波串高频振荡。此时的气动力整体上呈现出低频振荡与高频振荡共存的状态。 图27 Ma=3.0流动结构Fig.27 Flowfield structures at Ma=3.0 马赫数进一步增大至5.0时(图28),只在进气道上压缩面存在分离泡,且位置更加靠后,斜激波可以直接打入进气道内部,可以正常进气。进气道内激波串相互作用,形成高频振荡。气动力整体上呈现出高频振荡的特征。马赫数7.0时的流动结构与马赫数5.0相似。 图28 Ma=5.0流动结构Fig.28 Flowfield structures at Ma=5.0 总体来说,随着飞行马赫数不同,入口激波形状、激波振荡频率及气动力振荡频率均存在差异。马赫数变化会导致激波高低频振荡的转化。在飞行器确定设计工况时,需要考虑飞行马赫数对进气道进气性能的影响。 高超声速飞行器在临近空间环境高速飞行时,由于来流大气稀薄、来流动压低导致控制舵面效率不足,使得采用单一的舵面姿态控制系统难以满足飞行器机动性和弹道控制的需求,必须采用喷流控制或喷流/舵面复合控制[53]。横向喷流由于结构设计简单、不工作时对流场影响小、气动响应迅速、控制效率高等特点[54-57],被广泛应用于高超声速飞行器气动控制系统。但在高超声速来流条件下,横向喷流与来流会形成很强的干扰流场结构,会在喷口上下游出现边界层分离与再附、自由剪切层失稳,多激波系、多旋涡系以及激波/边界层干扰等复杂流动现象[58-60]。 国外学者早在20世纪50年代末就开始了对侧向喷流控制技术及其干扰机理的研究,国内相关工作起步较晚,始于20世纪80年代。研究采用理论分析、工程估算、风洞试验和数值模拟的方法,分析了喷口参数(位置、形状、数量等)、喷流参数(马赫数、流量、喷流压比、喷流介质和组分等)、来流参数(马赫数、雷诺数、迎角等)对横向喷流干扰特性的影响[61],从流场建立过程方面分析了喷流非定常流场建立与消退过程[62],从物理化学过程方面分析了真实气体效应对横向喷流干扰的影响[63]。这些研究较为系统地给出了横向喷流流场特征和喷流干扰机理。但同时也注意到,横向喷流多位于模型前体和中部,位于模型后体的情况研究较少,特别是扁平升力体类构型,由于发动机安装位置限制,喷流置于飞行器底部的横向喷流研究少见;喷流和舵面同时工作时,喷流对舵效影响的研究较少。 基于NNW软件,针对底部横向喷流开展数值模拟研究,分析底部横向喷流流场特性及对舵面效应的影响规律,为相关飞行器控制系统设计提供技术支撑。研究对象为升力体构型,控制机构包括底部的控制舵和多通道喷管组合结构,喷管布局示意见图29。 置于底部的喷流发动机采用单喷/多喷的组合实现对俯仰、偏航、滚转3个通道的控制。1#喷管为俯仰控制,4#喷管为偏航控制,2#和3#同时开启为滚转控制。底部横向喷流最显著的特征是喷流出口压力与当地压力比值极大,高超声速飞行器底部压力接近真空,喷流开启之后,燃气气体极速膨胀,对底部流场结构和附近的舵面流场结果产生较大影响,进而影响整体气动特性和舵面控制效率。 2.3.1 底部横向喷流干扰流场分析 数值模拟了3个控制通道的典型流场,计算网格采用结构对接网格,全场网格量约2 000万,图30给出了1#喷管开启时喷管附近的流场结构。高压气流在高速离开喷管后迅速膨胀,受弹体底部和腹鳍物面的限制,在这些部位附近形成复杂的激波结构,导致底部及下表面形成相对的高压分布,在下表面的物面附近产生强逆压梯度,导致流动发生分离,在腹鳍底部附近的部分区域形成回流。下表面的高压区起到了增大低头力矩的作用。在气流到达底部及腹鳍边沿缘后,与前体激波层内的超声速气流发生碰撞而在各自的前进方向形成激波,同时又和激波层外的高超声速来流相互作用形成强激波,从而整个区域呈现显著的激波/激波干扰现象,形成范围很大、强度很强的弓形激波结构,导致局部区域的高温分布(最大值达9 000 K以上,如图31所示),在如此高温条件下,真实气体效应可能会变得尤为显著。 图30 1#喷管开启的流场结构Fig.30 Flow field structure at the open of 1# nozzle 图31 底部截面温度分布Fig.31 Distribution of temperature on bottom 2.3.2 喷流对舵面效率的影响 从流场结构分析来看,喷流形成的干扰区距离升降舵较近,甚至出现喷流燃气直接打到舵面的情况,将会对舵面压力产生较大影响。表1分析了3个通道喷流对升降舵舵效的影响程度,喷流开启后升降舵舵效有明显变化,俯仰和滚转通道方向为迎风面喷流,显著增大舵面迎风面压力,使得舵面效率增大约20%,而偏航方向喷流产生的吹吸效应对舵面压力的影响比较复杂,会使得舵面效率降低约10%。喷流对舵面效率的显著影响,需要在飞行器控制时引起关注。 可操纵性是气动设计的主要内容之一[64],开展飞行器在舵面操纵下的动态响应过程模拟,获取动态响应参数,对提升飞行器的动态响应品质至关重要。如研究飞行器在升降舵阶跃舵偏操纵下攻角的振荡过程,可以获取超调量、峰值时间、调整时间以及上升时间等时域响应特性[65];而研究谐波型舵偏操纵下飞行器运动过程,可以获取响应带宽、谐振峰值等频域的响应特性。上述时域和频域响应参数都是飞行器设计的重要指标。 模拟飞行器在舵面操纵下的动态响应过程,主要应用到NNW软件的动网格技术和非定常流动/飞行器运动一体化耦合模拟技术。 计算选用方形截面导弹外形(图32),其主要特点是雷达反射面小,有利于隐身;可充分利用内埋弹舱空间,提高载弹量;平面外形能提供更高的升力等。针对该外形,分析了飞行器俯仰运动对阶跃舵偏操纵的动态响应特性,半场计算网格约350万。 图32 方形截面导弹外形和表面网格Fig.32 Geometry and grid of square cross section misssile 舵面的偏转按以下函数形式给出: (4) 式中:δ0和δm分别为初始舵偏角和舵偏幅值,δ0=0°,δm根据需要选取。在实际计算中,为减少初始流场建立过程对计算的干扰,开始阶段飞行器先不引入舵面运动,飞行器在自身气动力作用下自由运动,在0.56 s时再引入舵面偏转,在0.61 s时舵面回复到原位置。 图33 转动惯量对导弹动态响应特性影响Fig.33 Effect of rotational inertia on missile dynamic response characteristics 图34比较了质心位置对动态响应特性的影响。在xc/L=0.47时,飞行器在攻角±10°范围内是静不稳定,0°配平攻角表现为鞍点;超出这个攻角范围之后,导弹转变为静稳定的,两个配平攻角±13°是稳定的结点。从图34(a)模拟结果可以看到,从配平攻角释放后,当舵偏引入的扰动较小时(δm≤8°),导弹的运动围绕配平点附近振荡并逐渐收敛;但当扰动较大时(δm=12°),俯仰运动会跨过静稳定区域,进入静不稳定区域,在较大攻角范围内持续振荡,运动特性极为复杂,不利于导弹的操纵。为了改善导弹的响应特性,可以通过调整质心,改变飞行器的静动态气动特性。图34(b)展示了质心调整到xc/L=0.42时,导弹的动态响应过程。调整质心后,飞行器只有唯一的配平攻角0°,且在较大攻角范围内都是静稳定的,从模拟结果来看,即便是较大的扰动,飞行器在扰动消失后,其俯仰运动仍然是收敛的。 图34 质心位置对导弹动态响应特性影响Fig.34 Effect of center of mass position on missile dynamic response characteristics 为追求“更快速、更灵活、更精准”等战术指标,以空空导弹、火箭弹等为代表的新型弹箭呈现出更大的长细比、更轻的结构占比和更大的过载等主被动设计特点,从而导致其弹性变形越来越突出[66-67]。结构低阶固有频率与飞行力学短周期模态比较接近,气动弹性和控制系统之间的耦合作用显著增强,会不同程度影响控制系统的精度与飞行品质,甚至导致气动伺服弹性失稳问题[68]。因此,在飞控系统设计中,对飞行器进行气动伺服弹性分析,已经成为现代飞行器设计过程中必不可少的重要环节[69-71]。以往工程设计中,多采用定常线化假设和刚体运动/弹性振动解耦模型在频域范围内开展分析[72],鉴于此类弹箭飞行姿态角等会在瞬间发生剧烈变化,导致飞行动力学问题研究中最为关键的气动特性呈现出非线性和非定常特征,同时多学科之间显著耦合效应也使得以往的气动力简化方法难以准确反映飞行器气动载荷的实时动态变化[73]。 开展大长细弹箭快速机动过程中的气动/结构/控制耦合问题的精细模拟,主要需解决3个关键技术:同时适应物面大尺度刚体运动和小尺度弹性变形的网格动态边界处理技术,能够获取高精准气动力/载荷特性的高效高鲁棒非定常流场CFD求解技术,以及能同时包含刚体运动和结构振动耦合效应的高保真动力学模型等。基于NNW通用软件的CFD求解模块和动网格技术,通过二次开发发展了同时包含气动耦合和惯性耦合的刚体运动/弹性振动耦合动力学模型(如方程(5)所示)[74],并引入PID控制环节(如方程(6)所示),建立了基于CFD的弹性飞行器气动伺服弹性问题数值仿真方法。 (5) (6) 式中:m、I0、V和ω为分别为飞行器的总质量、转动惯量矩阵、质心速度以及绕质心的角速度;ωss表示矢量ω的斜对称矩阵;F和M为作用在飞行器上的合外力和相对于质心的合外力矩;hij为第i阶和第j阶结构振型的协变量矩阵;ηi和ηj为对应第i阶和第j阶结构振型的广义位移;Mij和Mii为广义质量矩阵的元素;Qi为对应第i阶结构振型的广义气动力;δcs为操纵面偏角值;KP、KI和KD分别为PID控制器比例、积分和微分环节的增益值;α和αcmd分别为飞行器的实时迎角和目标指令迎角;q为飞行器绕质心的俯仰角速度;θe为陀螺仪所在位置由结构变形引起的俯仰方向变形角。 计算网格包括弹身的静止域网格以及两片升降舵的运动域网格(图35),图36给出了3套体网格经过嵌套网格方法处理前后不同位置的切片,可看出所用的嵌套网格方法生成的网格嵌套区域和嵌套边界都比较合理。本文设计的来流马赫数为3.0,飞行高度设定为10 km,基于弹身直径的雷诺数为9.16×106。为了描述模型的结构弹性变形,这里选取模态分析所获取的具有代表性的4阶模态用于弹性特性计算,包含弹身的前两阶弯曲模态和升降舵的一阶弯曲与一阶扭转模态,具体数据见文献[75]。 图35 计算网格Fig.35 Computational mesh 图36 嵌套网格处理前后的计算网格切片Fig.36 Clips of computational grid before and after nesting operation 仿真导弹以马赫数3.0的速度飞行,在t=0 s 时刻给定20°迎角的拉起指令,不同模型的响应历程如图37所示。不考虑弹性效应时,图37(a)的仿真结果表明,该导弹在所设计的控制环节作用下飞行迎角能够在0.5 s左右达到控制指令,且不存在超调量,可以实现稳准快的操纵要求。而同时考虑结构振动对闭环控制系统的影响时,在不加入振动抑制措施的情况下,如图37(b)所示,弹性模型的飞行迎角也能够短时间内快速趋向于指令要求,但之后会在目标迎角附近振荡,且呈不断发散特征,这表明原来按照刚体模型设计的控制律应用到弹性模型时,由于纳入弹性振动效应,原来稳定的闭环飞行动力学系统会出现典型的气动伺服弹性发散问题。 考虑到结构在受到动态载荷激励后必然产生弹性振动,在操纵反馈过程中,传感器所采集到的运动信号中包含的振动信号会对导弹的实时刚体运动速度、质心位置等平动特征和角速度、姿态角等转动特征造成“误判”。图37(c)给出了只考虑弹性效应对平动特征的影响,即在控制环节中去掉了弹性效应对传感器转动信号的干扰,可以看出,飞行迎角能够在0.6 s内快速振荡收敛到目标,这与刚体模型达到目标指令的响应时间基本一致。 图37 不同模型升降舵偏角和迎角的响应历程Fig.37 Response history of control surface’s deflection angles and angles of attack for different models 从飞行力学特征模态角度分析相关机理,俯仰角变化属于飞行器短周期模态的运动特征。对于短周期模态,由于运动历程发展迅速,需要控制系统做出快速操纵反应,因此在飞控系统设计时除了要求其稳定外,还需保证合适的阻尼。考虑到弹体一阶弯曲模态的固有频率也与短周期模态频率更接近,特别是引入反馈控制环节后,弹性振动对传感器采集到的角速度等造成了干扰,从而使对稳定性有苛刻要求的短周期模态产生耦合失稳现象。相比之下,质心运动属于导弹长周期模态的运动特征,由于发展缓慢,只要不出现非周期发散情况,也容易被控制系统来操纵。因此,即使传感器纳入了弹性振动对速度和加速度的干扰,也不容易对长周期模态的稳定性产生定性的影响,只是定量改变了响应的历程。 飞行器的动态稳定性是指飞行器受到扰动后保持原来飞行状态的能力,通常用动导数进行表征,是动态气动特性设计、弹道设计及动态稳定性分析中的关键参数。高超声速飞行器再入时,其周围空气温度可达上万度,气体在高温作用下发生离解、电离,并发生复杂的化学反应,出现化学平衡/非平衡效应和热力学平衡/非平衡效应,即所谓的高温真实气体效应,对飞行器力/热特性、目标特性以及动态特性等产生复杂影响。 研究真实气体效应对飞行器动态稳定性的影响,涉及热化学反应、非定常流动以及飞行器运动等多种特征时间尺度问题的耦合模拟。鉴于数值模拟的难度,以往的研究多关注平衡气体对动态稳定性的影响,对化学非平衡气体则较少关注[76-78]。NNW软件建立了比较完备的真实气体效应模拟能力,在自主开发的软件框架下有机集成非定常、运动等功能,具备化学非平衡效应对动导数影响的研究能力。在真实气体效应模拟方面,NNW软件目前具有热力学一温度和两温度模型,可以考虑5、7、11组分等不同气体组分的化学反应过程,壁面催化特性包含完全催化、完全非催化以及有限催化等。在研究化学非平衡效应对飞行器动态稳定性影响时,化学反应模型采用Park的7组分模型,采用强迫振荡方法计算飞行器的动导数。 图38比较了考虑真实气体效应的返回舱标模热流计算结果,图中标注为LENS的曲线是实验结果,标注DPLR的为国外软件数值计算结果,均来自文献[79],标注FCW、NCW和r=0.01的曲线为NNW软件的计算结果,其中,FCW为完全催化条件计算结果,NCW为完全非催化条件计算结果,r=0.01为有限催化条件计算结果,计算结果与文献值吻合很好。图39比较了ELECTRE钝锥外形采用完全气体和化学非平衡模型计算的对称面温度分布云图,计算马赫数Ma=13.0,高度=53.5 km,计算网格量约为300万。从图39可以看出,考虑化学非平衡效应后,由于化学反应本身是一个吸热的过程,计算得到的激波层内气体的温度明显降低,同时激波位置也更贴体。 图39 钝锥温度分布云图Fig.39 Temperature contour of blunt cone 图40 俯仰力矩迟滞圈比较Fig.40 Comparison of hysteresis loop for pitching moment 1) NNW软件集成了较为完备的转捩模型、湍流模型、RANS-LES混合模型,开发了WENO、WENN等高精度算法,基本可同时实现强激波捕捉和边界层高精度模拟。 2) 针对不同应用需求,用户可基于NNW软件进行二次开发,满足特殊场景的用户需求。 3) NNW软件具有良好的架构设计,可实现跨学科之间的耦合模拟,如化学非平衡流动、飞行器运动、结构振动以及控制系统等之间的耦合模拟。 致 谢 向应用团队成员王新光、董思卫、华如豪等深表谢意,感谢NNW软件开发团队、测试团队和推广应用团队的技术支持。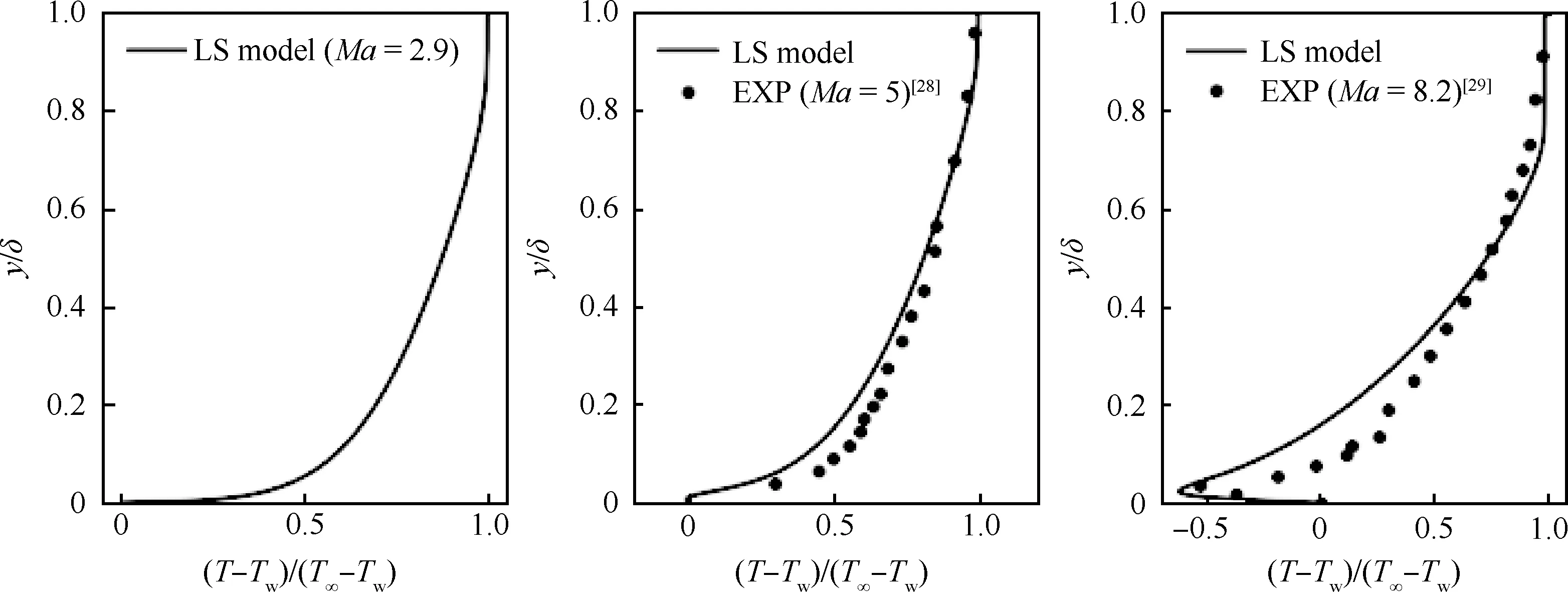
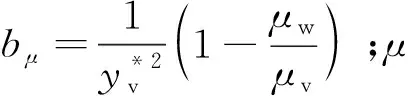




1.4 转捩过程高精度模拟



2 复杂干扰机制高清晰认知
2.1 钝舵缝隙局部流场数值模拟





2.2 进气道激波振荡的物理机制
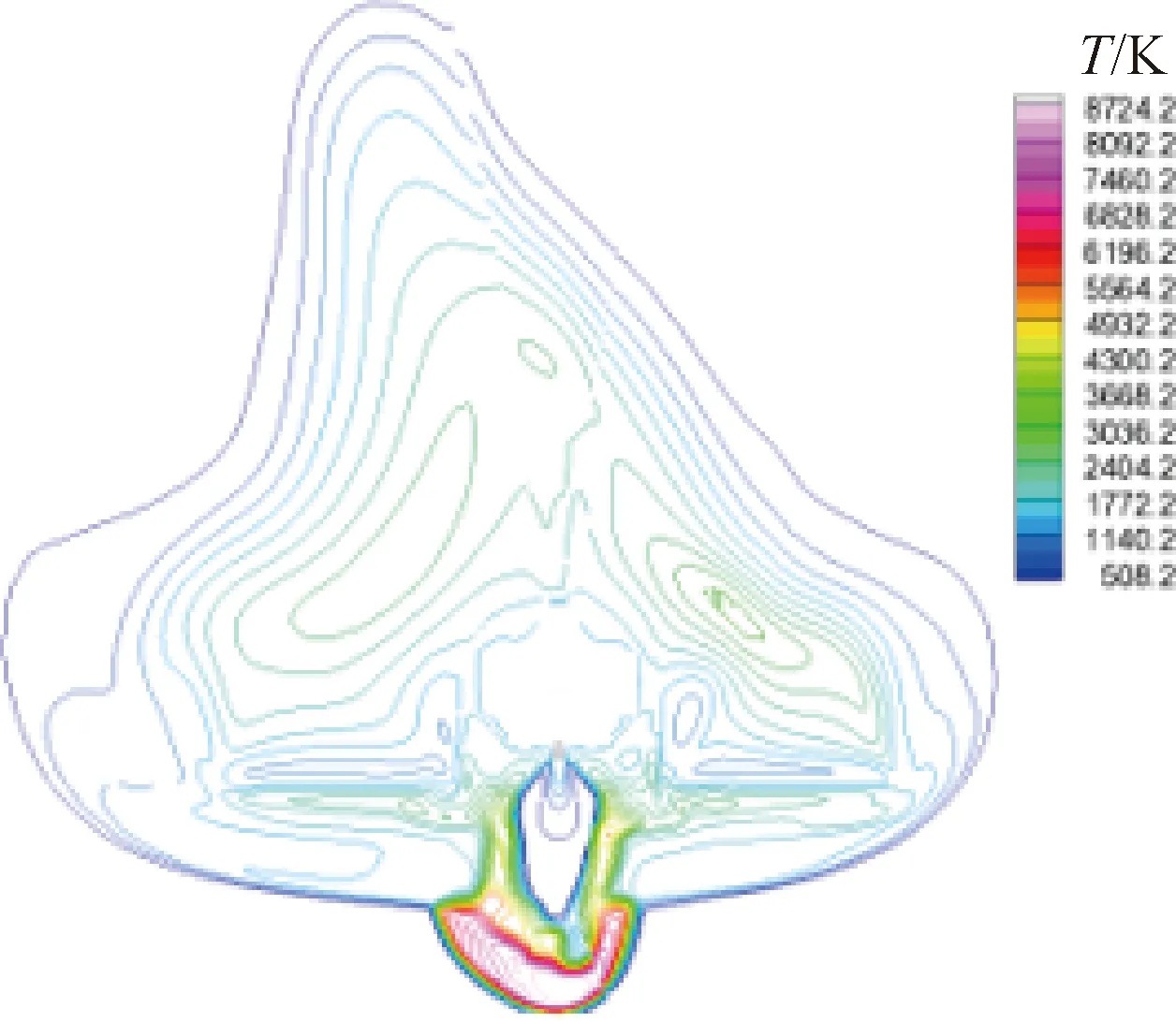
2.3 喷流干扰诱导回流激波机制
3 多学科耦合应用
3.1 方形截面导弹舵面操纵动态响应特性




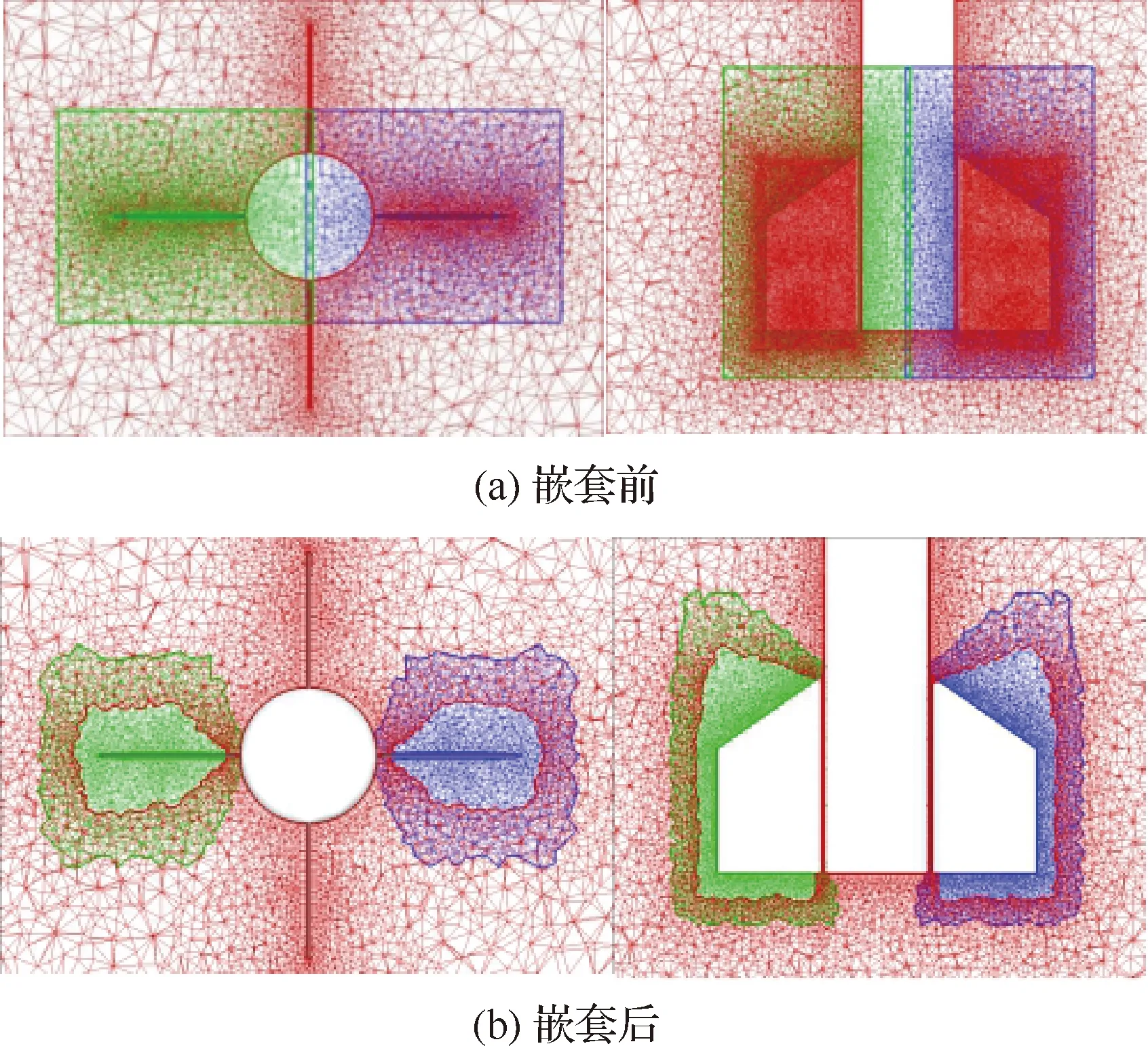
3.2 大长细导弹快速拉起过程的气动伺服弹性特性


3.3 考虑化学非平衡效应的动态稳定性计算


4 结 论
