高马赫数层流摩阻数值计算精度
2021-10-20范月华段毅周乃桢杨攀
范月华,段毅,周乃桢,杨攀
中国运载火箭技术研究院 空间物理重点实验室,北京 100076
飞行器在高空高速飞行的显著特征是高马赫数和低雷诺数,此时黏性与黏性干扰效应十分显著,极端工况下摩擦阻力在总阻中的占比甚至超过90%[1],对飞行器升阻特性等关键气动性能影响显著。因此,准确预估飞行器的摩擦阻力具有重要意义。
目前,地面试验还无法覆盖实际飞行工况[2-4],而飞行试验中还缺乏可行的科学测量手段获得有效的摩阻数据[5],因此计算流体力学(Computational Fluid Dynamics, CFD)技术是高空高速状态下摩阻预示最为有效的手段。近几十年来,随着CFD技术的不断突破和发展[6],航空航天气动设计的基本问题越来越多地依赖这一技术开展研究[7],但与飞行器阻力特性密切相关的摩擦阻力的精确预示一直是CFD的难题和热点之一。飞行试验结果分析发现,通过数值计算确定的轴向力系数与试验辨识结果存在较大差异,主要是由摩阻预示的不准确造成的。基于现有的认识,即使考虑高温气体效应和稀薄气体效应的影响,也无法充分解释上述摩阻预示的差异。结合地面风洞试验的结果,该差异主要源于数值计算的摩擦阻力结果偏高。因此,需紧密结合高空高速飞行特点,系统研究数值方法对摩阻计算精度的影响,为黏性效应的精细化模拟提供支撑。
在前期工作中,周丹等[8]研究了网格分布、通量格式、限制器对低速平板层流摩阻计算精度的影响,郑世超[9]研究了插值格式精度、通量格式和网格雷诺数对于高超平板层流摩阻计算的影响,张培红等[10]研究了提高混合网格摩阻预测精度的熵修正方法。但上述研究均以平板或者低速流动为研究对象,对于实际高速飞行器外形摩阻计算精度的相关研究仍较少,无法为高马赫数流动中黏性效应的精细化模拟提供支撑。
本文以具有高速飞行器典型部件特征的球锥、大后掠角三角翼为对象,结合风洞试验摩阻测量结果,研究了数值计算中影响摩阻计算的数值耗散及边界条件等重要因素,并基于分析结果提出了对CFD技术的发展需求。第1节首先介绍表面摩阻计算与试验测量结果存在差异的现象,第2节分析数值计算中影响表面摩阻的几个重要因素,第3节基于分析结果提出CFD技术的发展需求,第4节给出了研究结论。
1 摩阻计算与试验测量间的差异现象
1.1 圆锥表面摩阻计算与试验对比
Meritt等[11]基于AEDC(Arnold Engineering Development Complex)9号风洞开展了圆锥模型的表面摩阻测量试验,试验状态包括层流、转捩、湍流3种不同流态。模型长度为1 551.5 mm(从理论顶点算起),半锥角为7°,底端面直径为381 mm,端头半径为0.15 mm;摩阻测量传感器安装位置距离理论顶点1 350 mm,位于迎风面中心子午线一侧,与其夹角为10°。模型及传感器的位置如图1所示,攻角(Angle of Attack,AOA)在xy平面内。
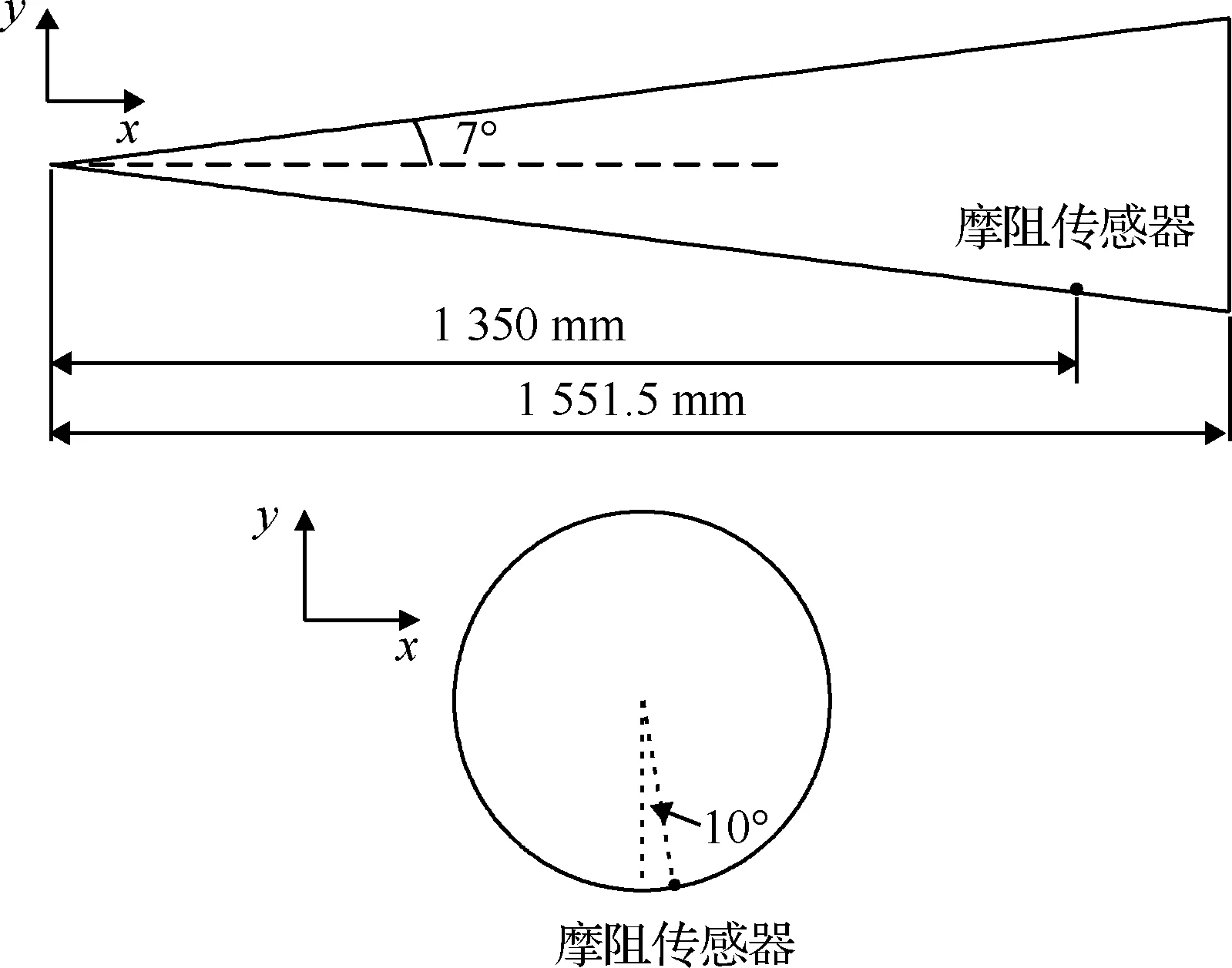
图1 Meritt试验模型及传感器位置示意图[11]Fig.1 Sketch of cone model and sensor location of Meritt[11]
分别使用国家数值风洞(NNW)工程研发的计算流体力学软件Flowstar[12](V1.0版)、商业软件CFD++和自研程序HyperCFD,针对其中的层流状态试验条件开展数值模拟,来流参数如表1所示。其中,Flowstar基于非结构网格,使用T-Rex技术保证边界层网格密度,边界层第1层网格高度为0.01 mm,无黏通量空间离散使用二阶HLLE++格式;CFD++和HyperCFD基于结构网格,计算网格边界层第1层高度为0.01 mm,无黏通量空间离散CFD++使用HLLC格式[13],HyperCFD使用Roe格式[14]。壁面温度均设为300 K。

表1 圆锥模型层流状态风洞试验参数
层流状态下测点处摩擦阻力系数数值计算结果与试验的对比如图2所示,可以看到,Flowstar的模拟精度与其他CFD软件接近,攻角α=10°时Flowstar相比于CFD++和HyperCFD分别偏大约4%和7%,不同软件的计算结果与试验测量结果偏差较大,相比试验偏大24%~30%。

图2 圆锥模型表面摩阻系数数值计算与风洞试验[11]差异Fig.2 Difference of skin friction coefficients of cone model between numerical calculation and wind tunnel test[11]
1.2 三角翼表面摩阻计算与试验对比
试验用三角翼标准模型全长363.34 mm,前缘后掠角为76.38°,分别采用摩阻天平和液晶涂层测量技术测量单点的摩擦应力和物面的摩擦应力分布,风洞来流参数如表2所示。摩阻天平测点位置在下表面中心线上,距头部顶点140 mm。

表2 三角翼模型风洞试验参数Table 2 With tunnel test parameters of delta-wing model
分别使用Flowstar、CFD++和HyperCFD对上述试验工况进行数值模拟。其中,Flowstar使用基于T-Rex技术的非结构网格,边界层第1层网格高度为0.01 mm;CFD++和HyperCFD同时采用2套结构化网格进行计算以评估网格密度对摩阻计算精度的影响:粗网格流向、法向和周向网格点数分别为147、81、327,边界层第1层高度为0.01 mm;密网格流向、法向和周向网格点数分别为301、301、327,边界层第1层高度为0.005 mm。壁面温度均设为300 K。
来流马赫数8、0°攻角下表面中心线摩阻系数层流计算结果与试验对比如图3所示。Flowstar获得的层流状态摩阻系数结果介于CFD++和HyperCFD之间,流向位置140 mm处Flowstar计算结果与HyperCFD结果相比约偏大15%;不同软件计算的摩阻系数都明显高于试验结果,流向位置140 mm处约为试验值的1.5~2.0倍。

图3 Ma∞=8、0°攻角下表面中心线摩阻系数层流计算结果与试验对比Fig.3 Comparison of friction coefficients along center windward ray between laminar calculation and wind tunnel test under conditions of Ma∞=8 and α=0°
通过以上2个计算与试验结果的对比,可以发现,即便不考虑流动转捩的影响,高马赫数层流的摩擦阻力计算仍然整体上高于试验测量结果。
2 摩阻数值计算精度的影响因素
计算网格是影响CFD计算结果的一个重要因素,在计算网格相同的情况下,不同的计算方法与设置也会对摩阻产生非常明显的影响。网格的影响不在本文的讨论范畴,本节仅关注CFD软件本身的计算方法与设置对摩阻计算的影响。如无特殊说明,本节计算均基于1.1节的圆锥模型开展,来流条件保持不变。
2.1 数值耗散的影响
使用自研的HyperCFD结构网格求解器对表1所列的层流风洞试验状态进行数值模拟,对比不同空间格式和熵修正方法对摩阻计算的影响,壁面条件为等温壁,壁温为300 K。
2.1.1 无黏通量格式
对比Roe、AUSM+[15-16]、Van Leer[17]3种不同空间离散格式对摩阻计算的影响,其中Roe和AUSM+格式使用MUSCL(Monotone Upstream-centered Schemes for Conservation Laws)插值得到空间二阶精度[18],同时使用minmod限制器防止激波振荡。此外,Roe格式需要采用熵修正来抑制非物理解的产生并保持计算稳定,常用的熵修正形式如下[19]:
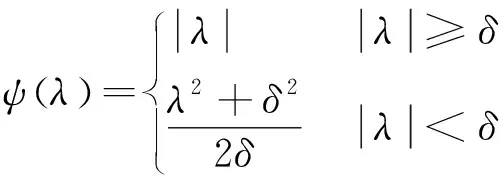
(1)
式中:λ为Navier-Stokes方程无黏通量Jacobi矩阵特征值;δ为熵修正阈值,当特征值的绝对值低于该值时进行熵修正。δ的值可以直接取常数,也可以表示为特征值的函数,根据δ的不同形成了各类熵修正公式[20]。
Van Leer格式属于矢通量分裂类格式,本身的数值耗散较大,黏性模拟精度较低,从而导致摩阻计算偏大,不适合进行边界层等强剪切流的模拟。Roe格式属于通量差分裂类格式,可以得到线化Riemann问题的精确解,对线性波的分辨率较高,因而对黏性剪切层的模拟也相对精确。图4 给出了圆锥模型不同空间格式测点摩阻系数的计算对比,其中Grid 1对应的网格边界层第1层高度为0.01 mm,Grid 2对应的网格边界层第1层高度为0.002 mm,Roe格式熵修正中δ的计算使用Müller提出的方法[21], eps0.1表示熵修正比例系数为0.1。可以看到,基于Roe和AUSM+格式的2套网格获得的摩阻系数基本一致,最大相差2%;Van Leer格式对空间网格的敏感度更高,20°攻角时2套网格的摩阻系数相差约8%。不同空间格式间的摩阻计算结果差异明显,而且随着攻角增加差异趋于明显;Roe格式计算的摩阻最小,AUSM+格式比Roe格式略微偏大2%~4%,Van Leer格式的摩阻最大,相比于Roe格式偏大20%~30%。结合相关理论及上述计算结果,可知黏性分辨率越高、数值耗散越小,黏性摩擦阻力的计算结果越精确。
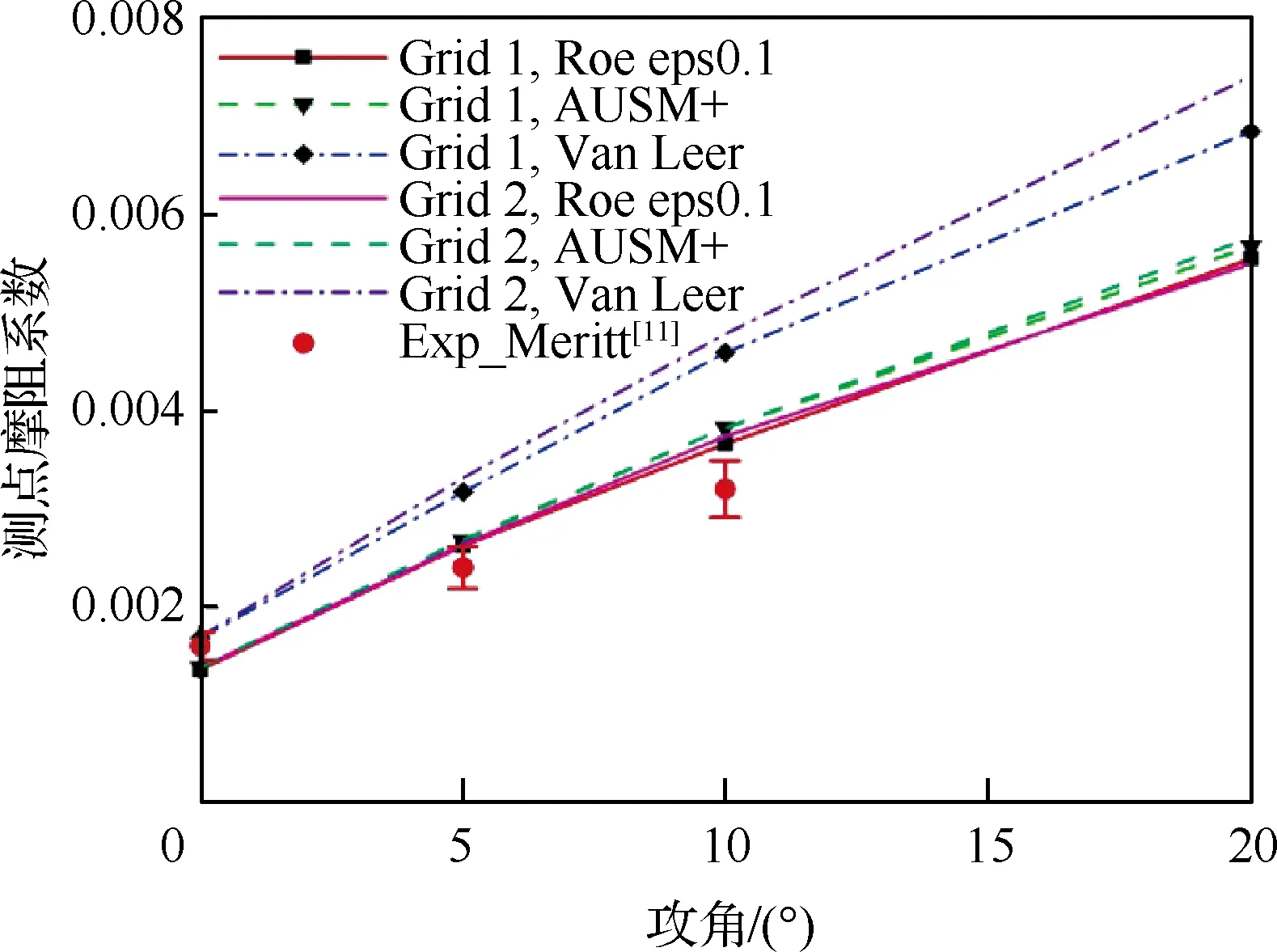
图4 不同空间格式测点摩阻系数对比Fig.4 Comparison of measurement location friction coefficients among different space schemes
2.1.2 熵修正方法
基于二阶Roe格式,对比Müller[21]和Harten-Yee[22]2种熵修正方法以及不同熵修正比例系数对摩阻计算的影响。2种熵修正方法均基于式(1),但是δ的取值不同,Harten-Yee熵修正方法δ的表达式为
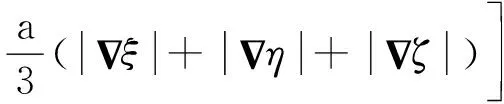
(2)
式中:δ*为熵修正比例系数;V为速度矢量;a为当地声速;ξ、η、ζ为计算坐标系的3个方向。Müller熵修正方法δ的表达式为(以ξ方向为例)
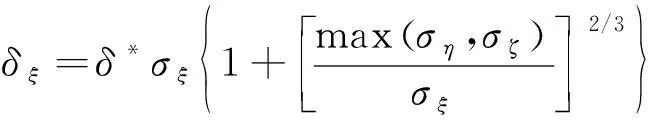
(3)

图5给出了圆锥模型不同熵修正方法和熵修正比例系数测点摩阻系数的计算对比。可以看到,2种熵修正方法的测点摩阻系数计算结果相差4%~8%,Müller型熵修正对黏性边界层的模拟精度更高。相比于Harten-Yee熵修正,Müller熵修正方法考虑了速度和网格的各向异性,对网格长细比较大的边界层区域具有更高的分辨率。此外,2种熵修正方法均表现为熵修正比例系数越大,Roe格式的数值耗散越大,计算的摩阻系数也相应越大。
从图5中可以得到的结论是,表面摩阻计算结果与格式的数值耗散特性密切相关,对于Roe格式而言,熵修正比例系数越小,计算摩阻系数越小。基于此,本文尝试在边界层内近壁区关闭熵修正,图6给出了这种处理方式下10°攻角时圆锥模型迎风面子午线(迎风面中心线)的摩阻系数,并与常规熵修正(Harten-Yee eps0.1)的摩阻结果进行了对比。

图5 不同熵修正方法测点摩阻系数对比Fig.5 Comparison of measurement location friction coefficients among different entropy fix methods
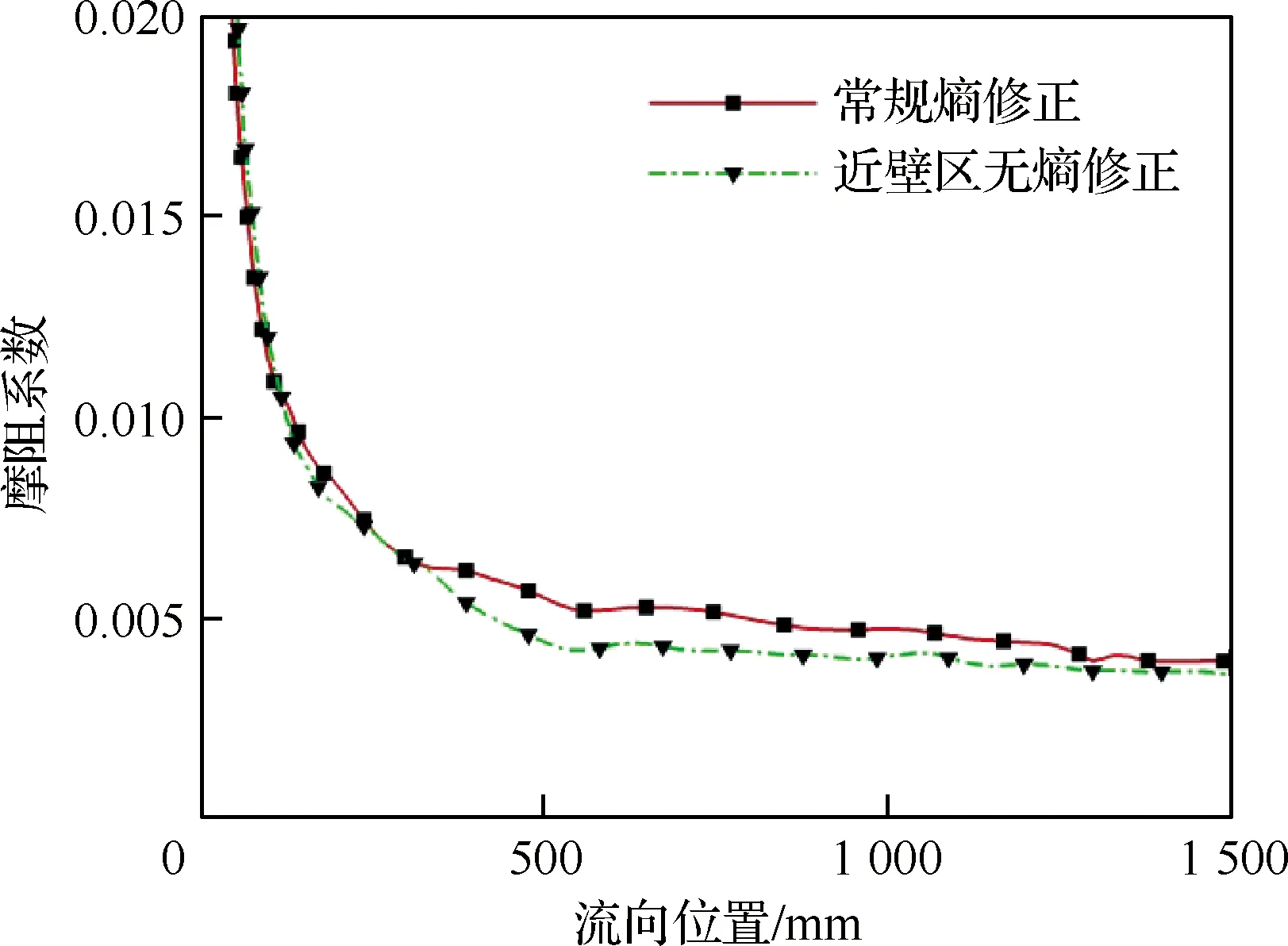
图6 近壁区无熵修正时10°攻角迎风面子午线摩阻系数Fig.6 Friction coefficient along center windward ray while closing entropy fix near wall under conditions of α=10°
可以看到,边界层内近壁区关闭熵修正得到的摩阻系数在120 mm后小于常规熵修正,在1 350 mm处偏小7%。然而由于处理方式比较简单,导致圆锥头部区域(120 mm之前)的摩阻系数有一定程度的增加。
2.2 壁面温度边界条件的影响
2.2.1 壁面温度
从低速到低超声速流动,来流总温较低,飞行器表面温度变化不明显,壁温对摩阻计算的影响问题不突出;而高马赫数飞行时,气动加热现象显著,计算时壁面温度的选取对于摩阻计算会产生较大影响。
第一,根据皖河流域山区环境的特点,构建低耗、优质、高产、高效的农田生态系统。主要内容有:山区土地整治和土壤改良,保持耕地的绿色覆盖,建设生态水系和现代灌溉系统,山坡耕地保护或退耕等。
对表1所列的层流风洞试验状态进行数值模拟,对比不同壁面温度条件对表面摩阻的影响,无黏通量空间离散使用二阶Roe格式,黏性通量使用二阶中心差分格式。图7给出了不同壁温条件下,圆锥模型在0°攻角(图7(a))和20°攻角(图7(b)) 迎风面子午线摩阻系数的对比情况,其中Tw为壁面温度。
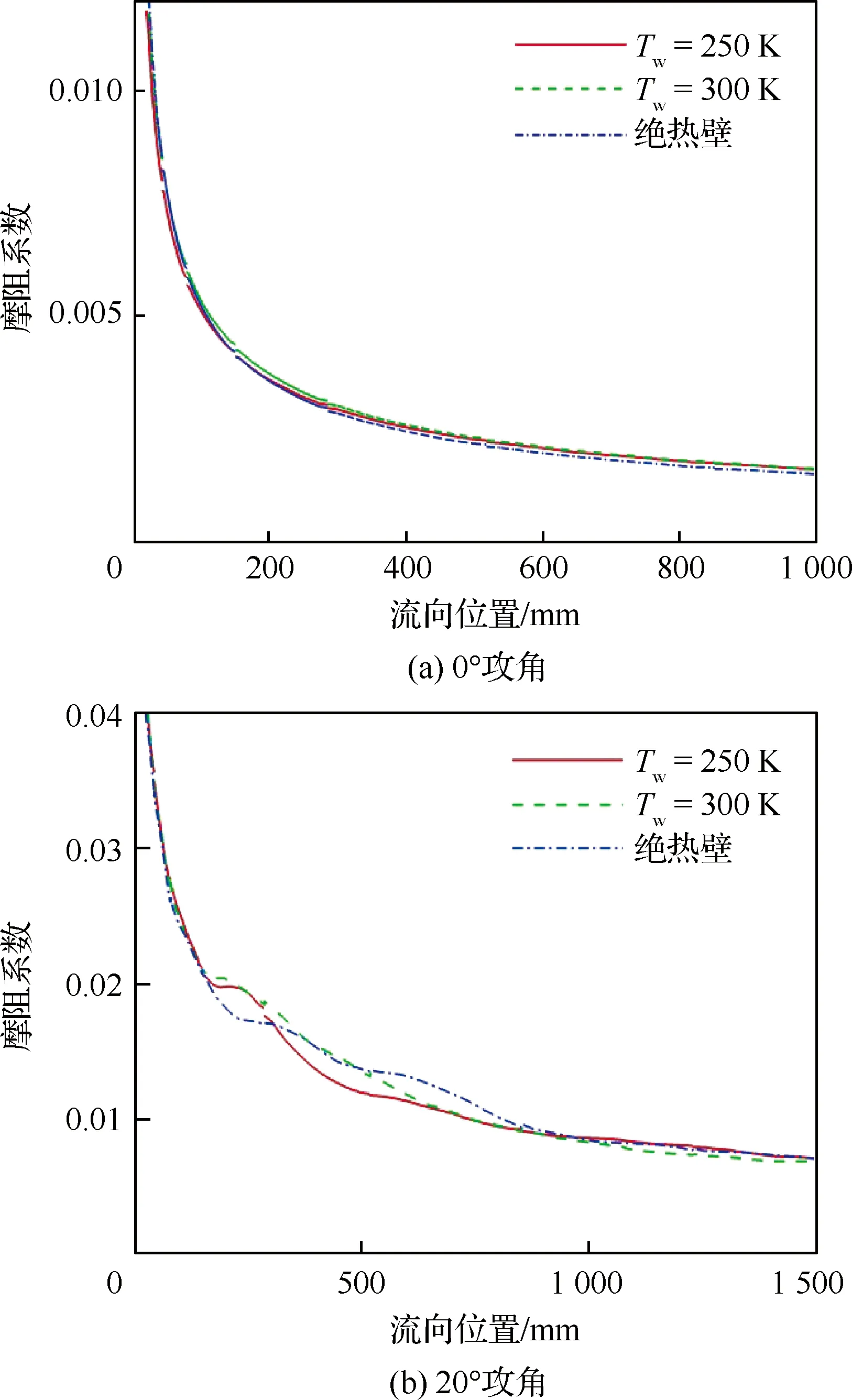
图7 不同壁温下圆锥外形迎风面子午线摩阻系数对比Fig.7 Comparison of friction coefficients along center windward ray of cone model at different wall temperatures
0°攻角时,边界层流动相对简单,壁面摩阻对温度边界条件不敏感,流向位置60 mm之前,绝热壁的当地摩阻更高;随着边界层发展,流向位置200 mm之后,绝热壁的当地摩阻低于等温壁。
20°攻角时,壁面摩阻随壁面温度的变化相对复杂。流向位置200~900 mm,壁温250 K(低壁温)对应的迎风面子午线的壁面摩阻小于壁温300 K的,二者在460 mm处最多相差13%;900 mm 之后,壁温250 K对应的迎风面子午线的壁面摩阻要更大,二者在1 220 mm处最多相差9%。这说明,当圆锥有攻角时,出现绕圆锥的横向流动,边界层内流动更加复杂,壁温对流场的影响较大;此时,不仅壁面附近网格上的耗散特性影响表面摩阻,整个边界层流动的模拟精度都会对摩阻产生较大影响。高马赫数流动时,不同物面位置处,壁温对表面摩阻的影响也不相同,这种现象对于复杂的飞行器外形更加突出,因此在进行数值模拟时真实壁面温度的选取对于计算结果的精度至关重要。
图8给出了三角翼模型在Ma∞=8来流中进行摩阻测量时红外测得的表面温度场,局部区域(尤其是头部和侧缘)气动加热明显。考虑到壁面温度设置对摩阻计算结果的影响,如果CFD软件能够实现基于边界层当地流场变量的壁面温度自适应调整,将有助于提高现阶段数值计算的摩阻预示精度。

图8 三角翼模型摩阻试验表面温度分布(Ma∞=8,T0=749 K)Fig.8 Surface temperature distribution of delta-wing model in friction test (Ma∞=8,T0=749 K)
2.2.2 壁面温度边界条件的表征方式
目前,高速流动问题的数值模拟通常采用等温壁面,数值计算中2种常用的等温壁面边界条件表征方式如图9所示,1代表壁面内第1层网格单元中心,w代表固体壁面,-1代表固体壁面外第1层虚网格中心。方式1第1层虚网格中心的温度T-1满足:

图9 2种常用的等温壁面边界条件处理方式Fig.9 Two common ways of isothermal wall boundary in simulation
T-1=2Tw-T1
(4)
方式2第1层虚网格中心的温度T-1满足:
T-1=Tw
(5)
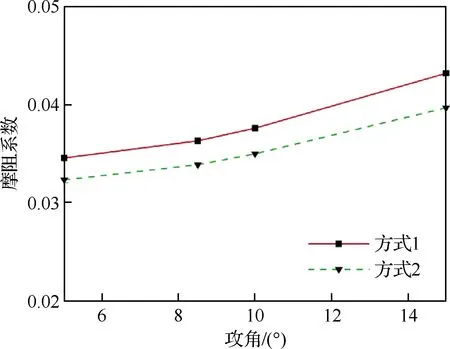
图10 高空高马赫数2种等温壁面处理方式飞行器摩阻系数对比Fig.10 Aircraft friction coefficients comparison between two ways of isothermal wall boundary at high altitude and high Mach number
2种处理方式对摩阻的影响可以通过雷诺比拟来解释。对于不可压平板层流流动,可以通过雷诺比拟建立摩阻系数Cf和斯坦顿数St间的联系[23]:
(6)
(7)
式中:Pr为普朗特数,层流一般取0.7~0.72;ρe和ue分别为边界层外缘的密度和速度;hw为壁面焓;haw为绝热壁焓;qw为壁面热流密度,其计算式为
(8)
其中:k为热传导率;T为流场温度;n为壁面法向方向。在数值求解Navier-Stokes方程时,基于网格中心的有限体积方法的壁面温度梯度的计算表达式为
(9)
其中:Δd为第1层网格中心与壁面的距离。由式(9)可知,图9中的表征方式1可以保证壁面处温度梯度不变,而表征方式2则会导致壁面处温度梯度偏小。结合式(6)~式(8)可知,使用方式2 进行等温壁面的温度条件处理会导致斯坦顿数St和摩阻系数Cf都相应偏小。摩阻和热流相关的计算主要涉及到速度和温度梯度的精确计算,目前的CFD方法中多以一阶离散为主,需要在现有基础上发展流场变量梯度的高阶表征方法。
3 摩阻精确预示的研究需求
通过本文对摩阻计算精度影响因素的分析发现,无黏通量离散格式的耗散特性和壁面温度条件对高马赫数流动的摩阻计算有重要影响。面向未来的工程应用需求,亟需依托于国家数值风洞工程发展高精度数值方法以精确模拟边界层黏性流动及其与激波、分离相互干扰作用中的流动问题,从而提高摩擦阻力的数值预示精度,具体需求包括:
1) 低耗散数值方法
计算的表面摩擦黏性应力与边界层近壁区数值方法的耗散特性密切相关,鉴于此,对整个流场可以采用不同区域不同耗散水平的处理方式——即分区低耗散数值方法,同时保证激波区域的计算稳定性和近壁区域的低耗散性。以Roe格式为例,可以采用基于当地流场参数的自适应熵修正方法,在近壁薄层内减小甚至关闭熵修正。但当边界层流动比较复杂,尤其流场变量梯度较大时,仅仅在近壁薄层内保证数值低耗散并不足以保证摩阻计算的准确性,需要发展高精度数值方法,提高边界层流动的整体模拟精度。
2) 基于边界层当地流场变量的壁面温度自适应调整技术
高速飞行时,来流的总温较高,气动加热现象往往比较严重,但是飞行器表面热流一般会随不同部位表现出巨大差异性,导致不同部位的表面温度差异明显。而高速流动时壁面温度与流场的相互耦合影响大,导致计算的摩擦阻力表现出很强的壁面温度相关性。现阶段数值计算中一般使用等温壁并将全局设为同一温度,其无法反映壁面温度的空间不均匀性。因此,需要根据壁面不同部位气动加热的程度,在给定基准壁面温度的基础上,发展可实现所有位置壁温的高效自适应调整技术。
3) 真实表面边界的建模和数值模拟方法
首先,材料与工艺水平会导致真实飞行器表面并不光滑;此外,高马赫数、长时间飞行时气动加热现象显著,飞行器表面材料出现熔解、烧蚀,产生质量引射并形成粗糙表面,这些效应与高速流动固有的高温、转捩等复杂流动效应相互耦合,对飞行器流场及摩阻等产生显著影响。因此,在重点发展的高精度数值方法方面,首先需要考虑层流状态下的粗糙表面、质量引射等边界的建模及数值模拟方法问题。
4) 高精度摩阻数值计算方法的验证
目前,可用于摩阻计算精度验证的试验数据仍十分缺乏,相关地面测量技术尚不成熟。相关研究已经获取的少量地面试验数据其精度和可靠性不足以支撑高精度摩阻数值计算方法的验证与改进。从计算方法的精度验证方面,需要开展能够反映典型流动特征的标准试验模型设计,系统开展精细化摩阻测量方法研究,并针对典型外形开展多种摩阻测量技术的对比验证风洞试验,研究并探索飞行试验摩阻科学测量技术,积累可靠的摩阻试验数据,为发展高精度数值模拟方法的验证提供数据支撑。
4 结 论
目前高马赫数层流的摩阻数值计算,相比于风洞试验测量结果仍然偏大,本文通过对无黏通量空间格式数值耗散和壁面温度边界条件对表面摩阻影响的计算和分析,得到了以下结论:
1) NNW-Flowstar在高马赫数(Ma=8~10)范围内,摩阻的计算精度与常用CFD软件相仿。
2) 表面黏性摩擦应力的计算精度与近壁区空间格式的耗散密切相关,数值耗散越小,表面摩阻的计算精度越高;在速度较低的边界层近壁区内关闭熵修正,将有助于提高表面摩阻的预示精度。
3) 高马赫数流动不同部位的壁温变化明显,进行数值模拟时壁面温度边界条件对表面摩阻的计算有重要影响。
4) 结合工程需要提出了高精度摩阻数值预示的研究需求,主要包括低耗散数值方法、基于边界层当地流场变量的壁面温度自适应调整技术、真实表面边界的建模和数值模拟方法、高精度摩阻数值计算方法的验证等。
致 谢
感谢国家数值风洞工程提供的网格划分软件NNW-Gridstar和数值计算软件NNW-Flowstar。
