国家数值风洞(NNW)工程中的CFD基础科学问题研究进展
2021-10-20袁先旭陈坚强杜雁霞郭启龙肖光明傅亚陆梁飞涂国华
袁先旭,陈坚强,杜雁霞,郭启龙,肖光明,傅亚陆,梁飞,涂国华,*
1. 中国空气动力研究与发展中心 空气动力学国家重点实验室,绵阳 621000
2. 中国空气动力研究与发展中心 计算空气动力研究所,绵阳 621000
随着计算机硬件能力的飞速提升,计算流体力学(CFD)已逐渐成为支撑武器装备、航空航天、交通运输和节能环保等诸多军民工业领域发展的核心手段。根据估算,波音飞机的设计过程中CFD已占据50%的份额,并预测随着CFD技术的发展,未来CFD将达到70%的份额[1]。
“数值风洞”是实现CFD技术应用于解决实际工程问题的重要工具,其研发建设在美欧等西方国家已经得到高度重视,目前国内市场上常见的与CFD相关的系列软件套装(包括网格生成、流场解算、多学科耦合分析与优化等),基本被西方国家产品垄断。2018年,中国启动了由中国空气动力研究与发展中心(CARDC)牵头建设的国家数值风洞(National Numerical Windtunnel, NNW)工程[2],旨在自主研发功能先进、种类齐全的CFD工业软件系统,建成拥有中国自主知识产权、国内开放共享的空气动力数值模拟平台。目前,已经面向全国发布了自主知识产权通用计算流体力学软件NNW-FlowStar、国内首款可控开源流体工程软件NNW-PHengLEI,在国内多家单位开始应用。
NNW工程套装软件的开发、优化与升级过程中催生了一批理论与关键技术创新,其中在软件架构、集成与测试、验证与确认等方面的主要进展在文献[3-6]中给出了较为全面的综述。
为了加强NNW工程套装软件在国防工业与国民经济发展中的重要作用,CFD基础理论方面的持续创新是必不可少的。以航空航天为例,总变差减小(Total Variation Diminishing, TVD)格式的提出及广泛应用为高超声速流动提供了高效鲁棒的求解方法,增强了CFD对高速飞行器气动力/热的鉴定评估能力;而高精度数值方法和大涡模拟(LES)理论的成熟使涉及边界层转捩、大范围分离湍流问题的CFD预测更加精确。因此,NNW工程在若干基础科学问题研究方面投入了大量资源,通过联合国内众多高校及研究机构,在湍流与转捩模型、多相多介质模型、多物理场耦合模型、高阶精度算法等方面取得了一系列阶段性的原创研究成果,对NNW工程软件系统的功能拓展和能力提升打下了坚实基础。
本文简要总结了NNW工程实施以来在若干基础科学问题方面取得的主要研究进展。随着工程进度进入后半程,满足一定成熟度要求的基础研究成果将会首先集成至NNW-PHengLEI软件并面向全国开源共享,经过充分的检验和改进后将进一步集成至面向流体工程应用的通用CFD软件。
1 转捩与湍流模型及计算方法
转捩与湍流是流体力学领域的两大“百年难题”,其复杂的流动机理至今尚未完全清楚[7]。为了满足中国工业CFD软件需求,NNW工程针对转捩与湍流预测模型及计算方法做了很多亮点工作,相应预测能力与精度均得到提高。
1.1 转捩预测模型
目前横流转捩模型预测速域主要集中在亚跨声速范围,多数模型不适用于超声速/高超声速横流转捩预测[8]。张毅锋等针对超声速/高超声速情况下三维边界层转捩面临的转捩机制复杂、影响因素多、缺乏标定数据等难点问题,基于γ-Reθ转捩模型,提出了合理的压力梯度修正、普朗特数修正[9],进行了横流转捩拓展,并开展了横流转捩模型参数不确定度分析[10]。陈坚强等[2,11-13]进一步拓展了高超声速横流转捩数据,构造了考虑表面粗糙度影响的高超声速横流转捩判据,提出了C-γ-Reθ转捩模型,并将该模型成功用于高超声速大攻角横流转捩预测,实现对带攻角锥的常规风洞试验/飞行试验、HIFiRE-5静音风洞试验的高超声速三维边界层转捩预测,预测结果与试验结果吻合良好(图1),并结合线性稳定性理论对HyTRV升力体表面的高超声速横流转捩开展了研究。
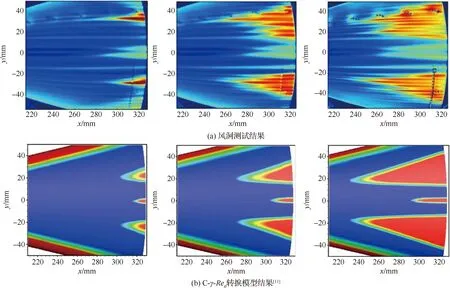
图1 HIFiRE-5横流转捩预测Fig.1 Prediction of cross-flow transition on HIFiRE-5
在转捩研究中,基于流动稳定性理论的eN方法被认为具有较为坚实的理论基础以及较好的精度。但传统稳定性分析与eN方法受限于积分路径等,对三维复杂问题实用性较差。黄章峰等[14]开展了感受性、三维边界层积分路线等方面的研究,基于广义增长率的守恒特性和三维扰动传播射线理论提出了改进的抛物化稳定性方程(Parabolized Stability Equations, PSE)、eN方法,显著提高了对一般三维复杂流动稳定性分析的计算效率和转捩预测可靠性。图2[14]对比了原始PSE方法及改进方法的预测结果,其中x表示沿着积分路径的流向坐标,A/Ax=110为横流波波幅比值,ω为圆频率,散点为直接数值模拟(Direct Numerical Simulation, DNS)计算数据,虚线为原始PSE计算结果,实线为改进方法(RTPSE)的计算结果。
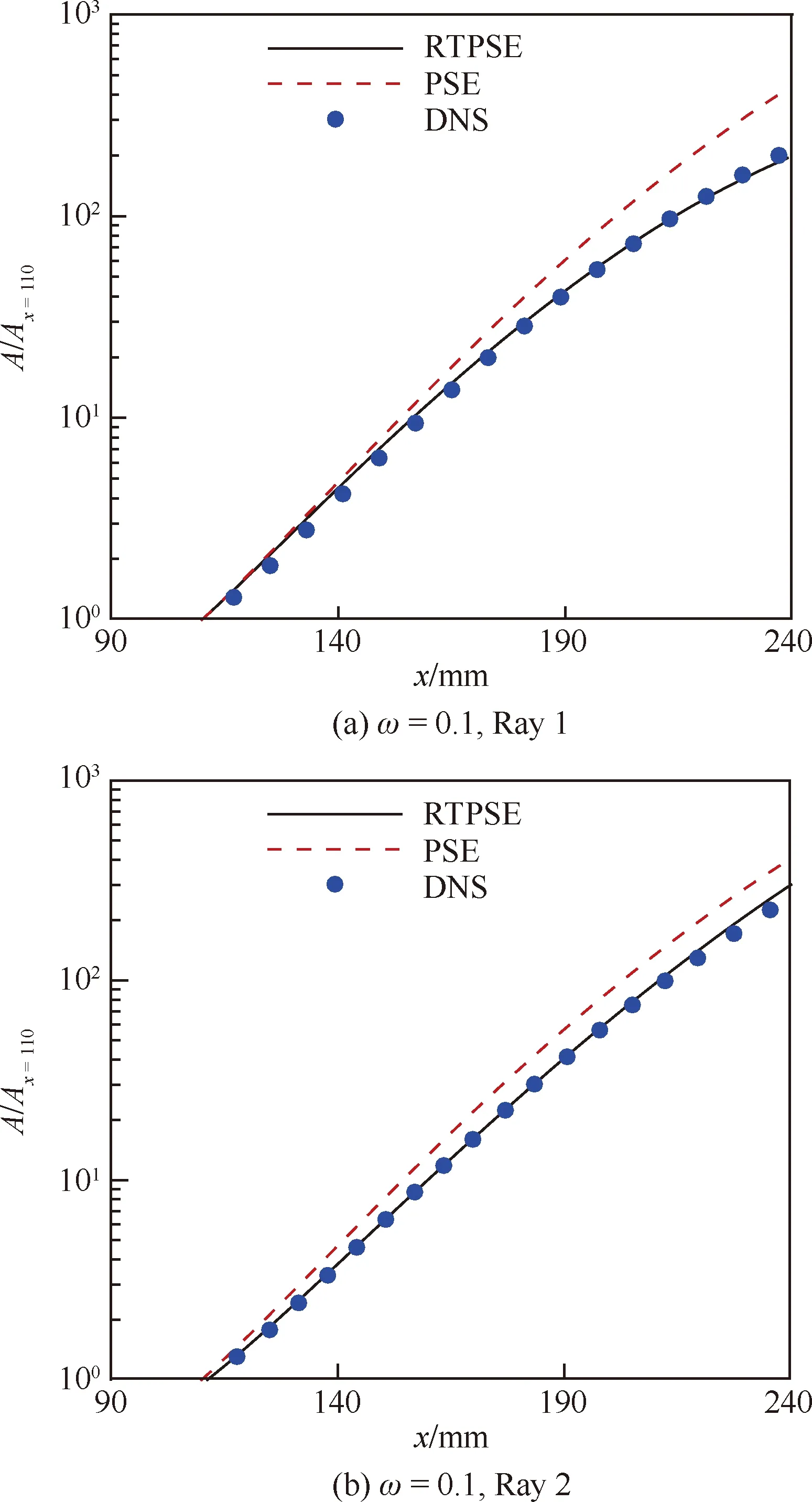
图2 新型PSE/eN方法预测结果[14]Fig.2 Prediction results of new PES/eN method[14]
毕卫涛等[15]基于结构系综理论(SED)提出了一种构建工程转捩模型的新思路,即通过试验和可靠的计算数据确定转捩边界层的结构系综,提炼反映转捩边界层物理状态和相似性的多层结构参数,进而形成物理图像清晰、定量描述精确的新型转捩模型。其研究结果表明该思路能够成功应用于刻画由自由来流湍流诱发的平板边界层强迫转捩和有攻角的高超声速尖锥转捩两类流动,图3[15]给出了6°攻角尖锥迎风面热流SED-SL模型预测结果与试验测量的对比,其中图3(a)为试验测得的温差ΔT云图,图3(b)为SED-SL模型计算得到的热流系数Ch,二者对比说明预测的转捩位置与试验取得了初步的一致性。
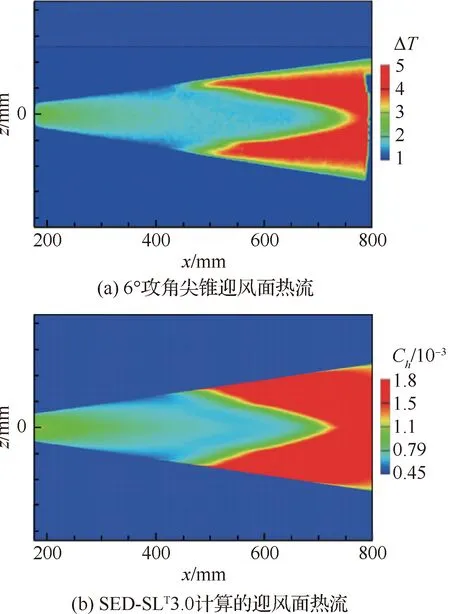
图3 6°攻角尖锥迎风面热流SED-SL模型预测结果[15]Fig.3 Prediction results of SED-SL model on windward surface in 6° angle of attack cone flow[15]
由于实际流动转捩对初值十分敏感,因此实际飞行条件和风洞试验条件之间的来流差异需要在各种预测模型中加以考量。涂国华等[16]对风洞试验和飞行试验的转捩N值进行了关联,发展了一种适合高超钝锥的转捩N值关联方法。此外,涂国华等[17]针对三维全局稳定性分析的Jacobian系数矩阵巨大、特征值不易求解的难题,提出了一种全局稳定性模态分解方法,可以有效实现复杂流动的全局稳定性分析。
1.2 湍流模拟模型
陈十一团队[18]开展了可压缩各向同性湍流的多过程分析方法和高保真度大涡模拟模型研究,基于亥姆霍兹分解和Kavasznay分解方法实现了可压缩各向同性湍流的多尺度性质分析,误差达到0.1%以内。通过使用人工神经网络方法,并结合可压缩湍流的物理机理,王建春等[19-20]发展了可压缩各向同性湍流的高保真度大涡模拟模型,图4给出了反卷积人工神经网格(Deconvolution Artificial Neural Network, DANN)结构示意图。新的大涡模型在先验验证中的相关系数达到0.95以上,在后验验证中,可以精确地预测能谱、结构函数等统计量,以及瞬态流场结构(图5)。
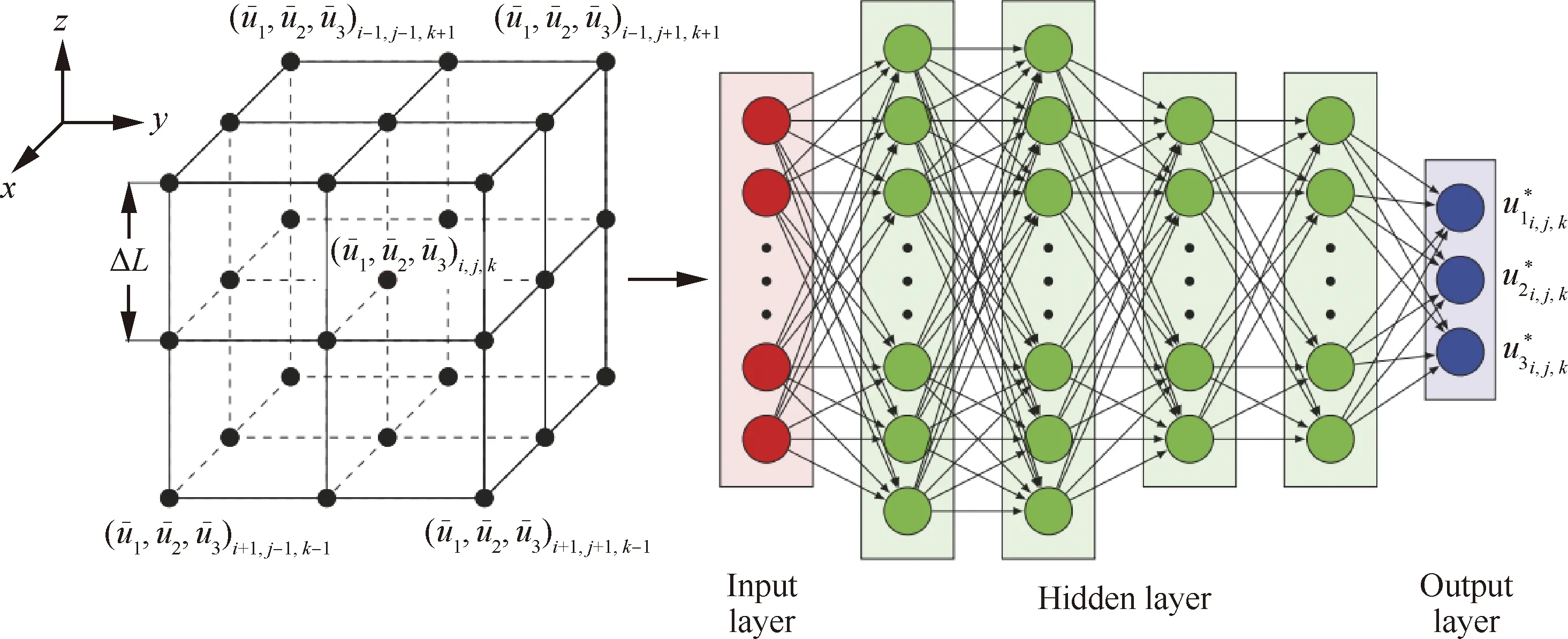
图4 反卷积人工神经网格结构示意图[19]Fig.4 Schematic of structure of deconvolutional artificial neural network[19]
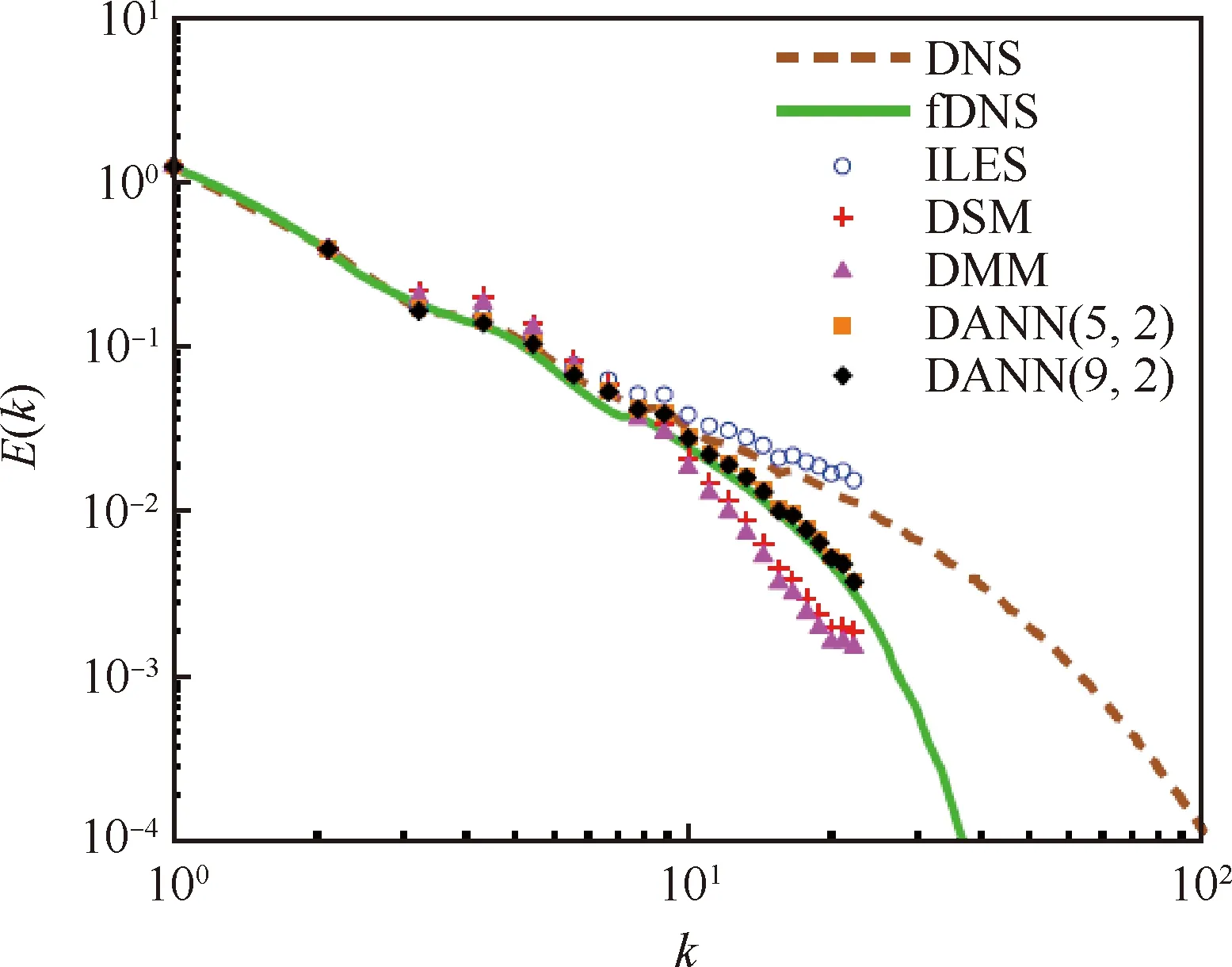
图5 DANN在各向同性湍流计算中的应用[19]Fig.5 Application of DANN in computation of isotropic turbulence[19]
针对高雷诺数壁湍流模拟网格需求过大的问题,吴霆等[21]实现了Werner-Wengle壁面应力模型的大涡模拟(LES)。
陈浩等[22]提出了一种基于分区混合和基于湍流尺度混合的双重RANS/LES混合模型,合理引入了壁面影响修正、网格拉伸修正以及多重过渡函数。在具有强非定常特性的大范围分离湍流模拟中,双重RANS/LES混合模型的预测结果较传统DES类方法有明显改进。
张伟伟等[23-24]结合量纲分析、标度理论以及神经网络机器学习方法,发展了可以独立于传统湍流模型的涡黏封闭方法,实现了将数据驱动模型与Navier-Stokes(N-S)方程求解器的动态耦合,并验证了方法对不同翼型/机翼/翼身组合体在不同马赫数、雷诺数、攻角等流动状态下的泛化能力。结果表明预测的气动力系数符合源数据(图6[24]),在一定流动状态范围内可以重现传统RANS模型的解,体现了机器学习方法在未来湍流模型化工作中的良好前景。
图6 NACA0012翼型表面摩擦阻力系数分布对比(实线:SA模型,符号:机器学习)[24]Fig.6 Comparison of skin friction coefficients on NACA0012 airfoil (solid-lines: SA model, symbols: machine learning)[24]
黄生洪等[25-26]针对湍流边界层入口条件生成问题,基于Kraichnan单波数脉动随机算法模型提出了一种入口边界湍流生成算法,即DSRFG(Discretizing and Synthesizing Random Flow Generation),成功解决了人工合成湍流产生符合预定湍流能量谱特性和空间相关性的入口条件(图7),图中f表示频率,fS表示不同频率Fourier模态的幅值,DSRFG从算法上精确满足了入口边界解的适定性(主要是湍流脉动的流量连续条件)。此外,DSRFG方法还具有良好的并行特性,目前已通过波数空间的log扩展,进一步使DSRFG方法能够产生大跨度波数空间湍流谱范围的脉动。

图7 DSRFG算法结合高精度大涡模拟结果[25]Fig.7 High-order LES result of DSRFG method[25]
2 多相多介质计算模型与方法
多相与多介质问题研究是航空航天、能源动力等领域的重要理论和关键技术基础[27],相关问题的数模模拟也对CFD技术的发展提出了极大挑战。为了拓展中国工业CFD软件的应用领域,NNW工程重点针对跨介质飞行器出/入水过程模拟、飞行器结冰与防除冰特性预测、流/热/固耦合热质传递分析以及热气动弹性预测等难点问题,发展了多类多相多介质计算模型及计算方法,有效提高了多相流数值预测的计算精度。
2.1 气/液两相流模型
准确捕捉气液两相界面是气/液两相流动过程模拟的核心问题。光滑粒子流体动力学方法(SPH)作为较流行的无网格粒子方法,具有拉氏计算准确描述物质界面的优势,能自然满足自由面边界条件,非常适合于模拟介质大变形等复杂现象。
施文奎等[28-29]发展了空间变光滑长度SPH方法和多自由度流固耦合模型,图8[28]给出了基于发展的SPH方法模拟带多自由度运动的三维返回舱水上回收问题的计算结果。将模拟结果与试验结果进行了定量比对,验证了方法和模型的有效性,分析了入水冲击现象和规律,拓展了SPH方法在复杂入水问题中的应用能力。

图8 返回舱水上回收模拟[28]Fig.8 Simulation of a space capsule water recovery[28]
张阿漫等[30]基于Roe近似黎曼求解器建立了多相流SPH模型,引入耗散项限制因子模拟黏性流动,保证了模拟大密度比复杂流动界面时压力场的光滑性和稳定性。针对三维轴对称问题,在柱坐标系下对轴对称SPH方程进行了全新的推导,建立了轴对称多相流模型[31],并通过经典的表面张力测试和气泡上浮算例验证了模型的有效性。图9[30]给出了Rayleigh-Taylor不稳定性问题求解的压力云图变化,图10[31]对比了不同Ar数和Bo数下的上浮气泡最终形状,与试验结果吻合较好。

图9 Rayleigh-Taylor不稳定性问题压力云图[30]Fig.9 Pressure contours of Rayleigh-Taylor instability problem[30]

图10 不同Ar数和Bo数下的最终气泡形状[31]Fig.10 Terminal bubble shape with different Ar number and Bo number[31]
刘谋斌等[32]发展了ES-FEM-SPH方法,利用ES-FEM方法处理结构变形,SPH方法求解流场信息,并发展了如图11所示的虚粒子耦合算法来传递单元-粒子交界面的物理信息,模拟了弹性挡板液舱晃荡减阻问题;同时将虚粒子耦合算法延伸应用到了流体-结构共轭传热问题中[33],突破性地基于FEM-SPH方法对传热-流体-结构耦合问题进行了模拟分析,图12给出了耦合过程中某一时刻的温度场云图。
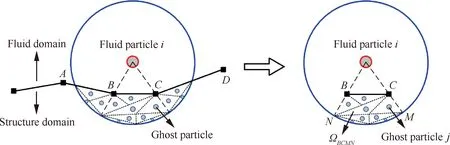
图11 单元与对应虚粒子耦合示意图[32]Fig.11 Schematic diagram of interaction between element segment and corresponding ghost particles[32]

图12 温度场云图(ES-FEM-SPH方法)[33]Fig.12 Contour of temperature with ES-FEM-SPH method[33]
2.2 飞机结冰模型
飞机结冰是多个物理过程综合作用下的复杂现象,既包含传热、传质和液体流动等宏观过程,又涉及晶粒形核和生长等微观过程[34]。
针对传统方法难以对三维孔隙结构进行定量表征的问题,李伟斌等[35]基于结冰孔隙呈球形、孔径取值连续、孔径服从特定分布等二维图像的合理假设,提出了基于结冰二维图像定量信息的三维微观结构建模方法。图13给出了1 cm3结冰三维孔隙结构的建模结果,d为孔隙直径,与实验结果的对比表明,该方法可行,为结冰精细化研究提供一种新途径。
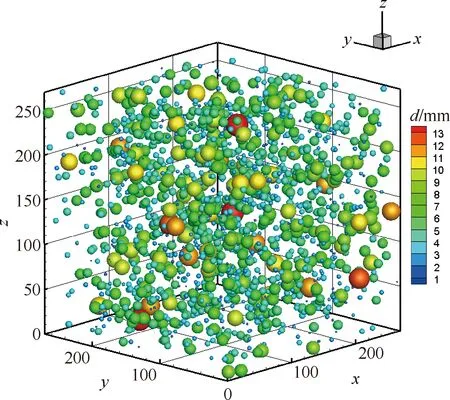
图13 1 cm×1 cm×1 cm结冰的孔隙分布[35]Fig.13 Pores distribution of modeling ice with size of 1 cm×1 cm×1 cm[35]
易贤等[36]根据光滑表面、粗糙表面及不同润湿性表面上液滴飞溅的试验结果,提出了更具普适性的液滴发生飞溅的临界条件预测公式,图14给出了预测公式计算结果与已有文献数据对比,验证了所提关系式的普适性。
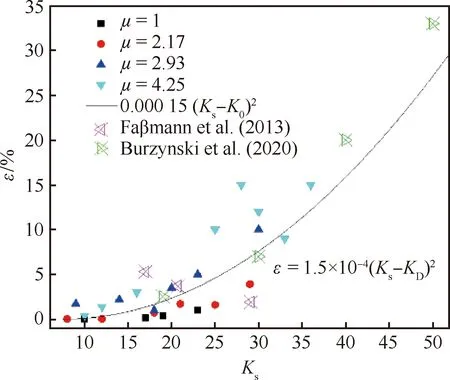
图14 飞溅量与飞溅参数之间的关系[36]Fig.14 Relationship between splashing quantity and parameter[36]
2.3 流/热/固耦合模型
未来高超声速飞行器在长时间飞行过程中,不仅涉及传统气动热、结构传热及应力变形等多因素耦合的流/热/固耦合问题,同时也需要进一步考虑新型复合防热材料的跨尺度效应和舱内热效应等综合热效应问题[37]。
杨肖峰等[38]根据高焓气流下表面反应传热过程的跨尺度动力学机理,建立了如图15所示的表面效应的CFD/RMD耦合计算方法,获得具有反应动力学物理意义的界面参量,提升了含多相催化效应的高超声速飞行器气动加热预测能力。
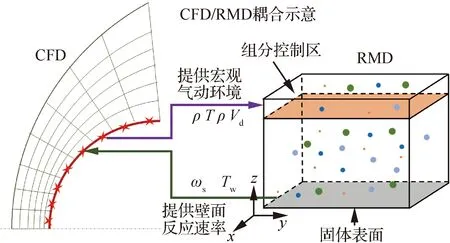
图15 求解表面跨尺度催化传热过程的CFD/RMD耦合计算[38]Fig.15 Transcale CFD/RMD coupling diagram of surface catalytic heat transfer process[38]
李明佳等[39]针对高温氧气氛下C/SiC复合材料内碳纤维的氧化烧蚀现象,首先通过阶梯逼近方法构建了C/SiC复合材料的三维几何模型,并基于格子Boltzmann方法建立了如图16所示的碳纤维的扩散-烧蚀模型,实现了氧化烧蚀过程中气体扩散和界面推移的耦合求解。
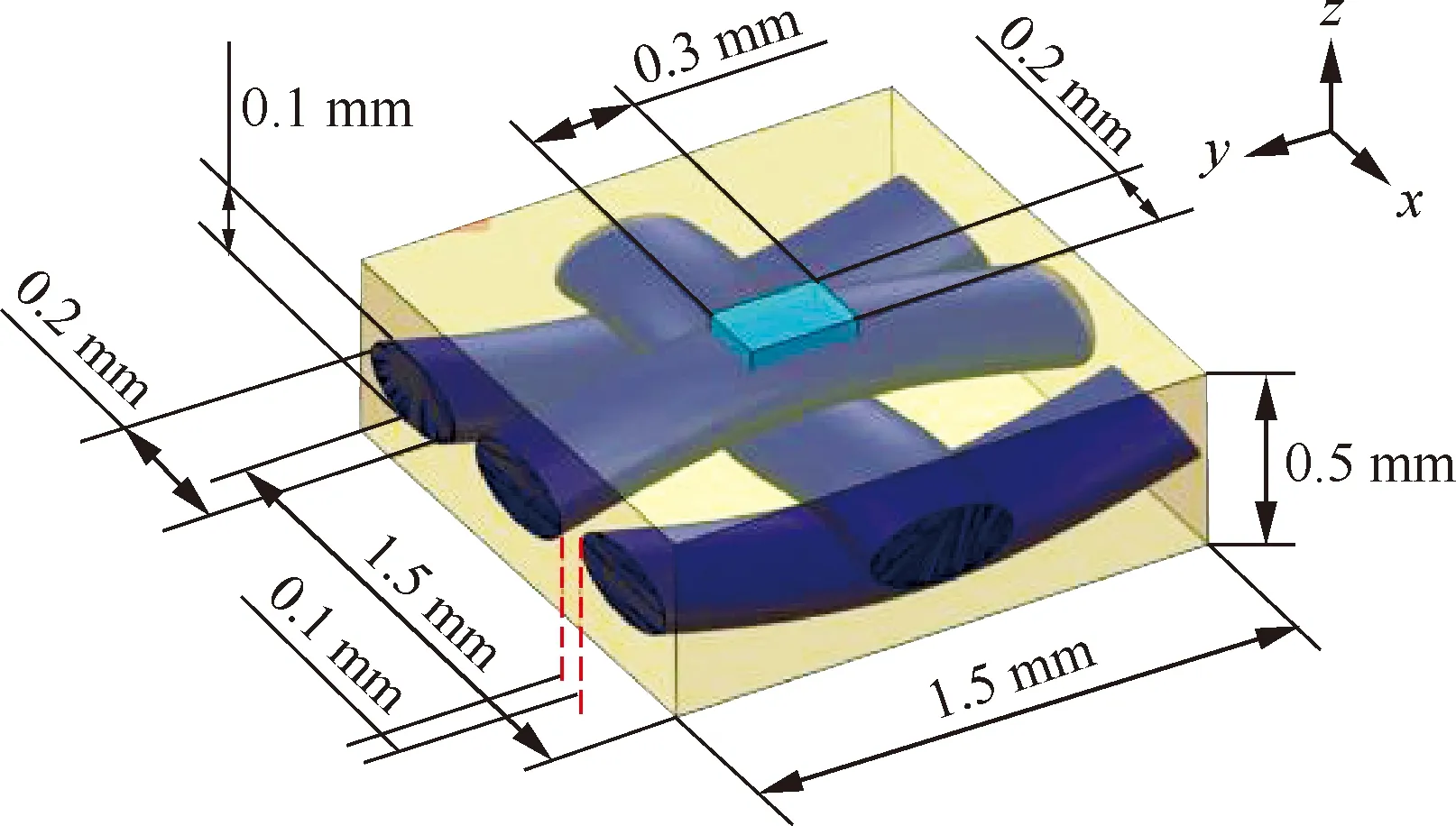
图16 平纹编织C/SiC复合材料三维介观烧蚀单元模型[39]Fig.16 3D ablation mesoscopic model of plain weave C/SiC composite[39]
张超等[40]发展了基于热格子Boltzmann方法及CPU/GPU异构并行算法,建立了一种适用于复杂构型舱内流动传热的数值模拟手段,实现了十亿量级网格规模的流/固耦合问题高效求解。图17给出了含人体模型的A320客舱内流场与温度场的精细化预测结果。
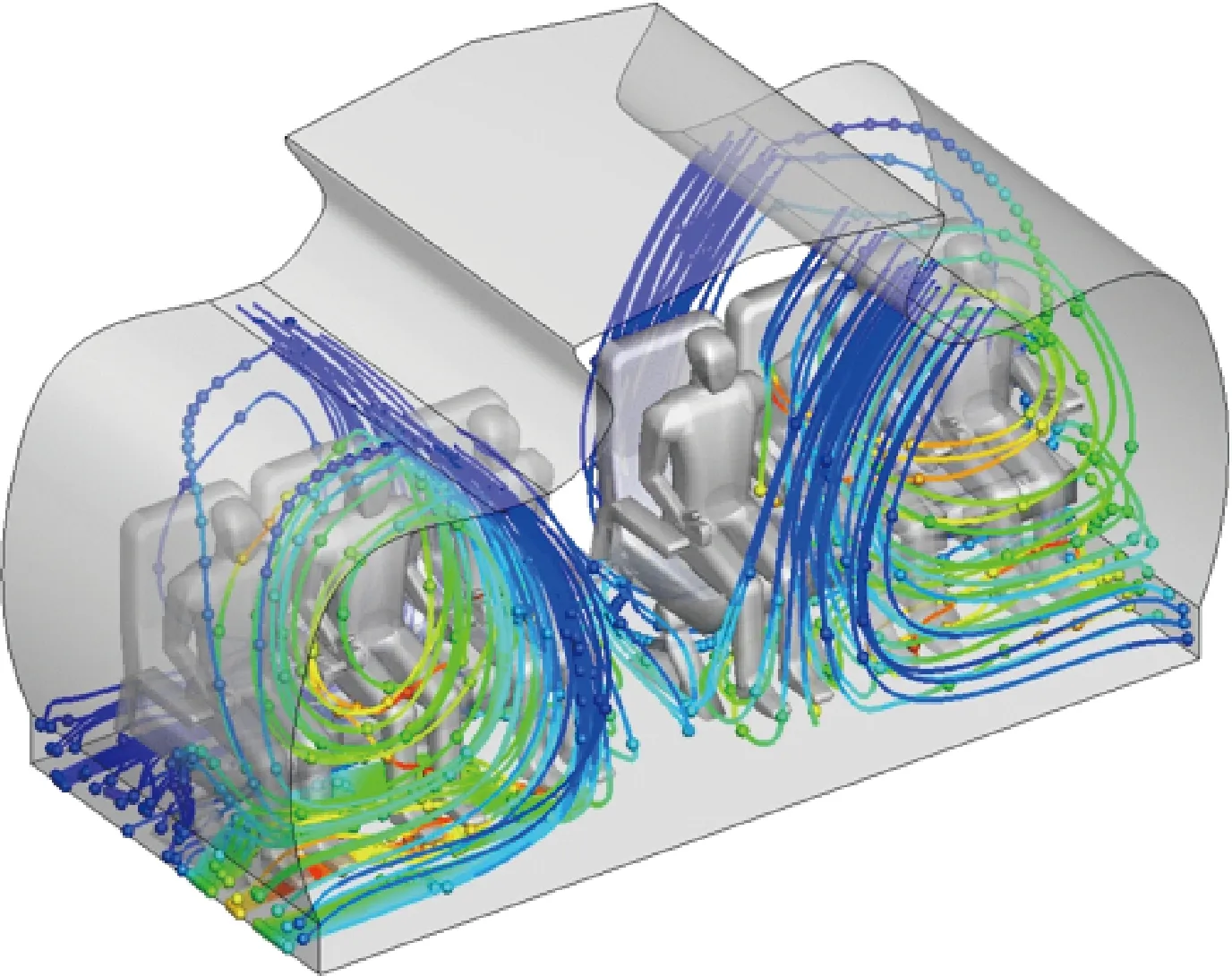
图17 基于热格子Boltzmann方法的A320舱内流场预测结果[40]Fig.17 Prediction results of flow field in A320 cabin based on thermal lattice Boltzmann method[40]
Chen等[41]发展了高温条件下固-固粗糙表面几何形貌表征与构建技术,并综合考虑界面多尺度传热、间隙辐射换热以及力/热耦合特性等,建立了典型防隔热材料固-固界面多尺度传热特性数值预测模型及数值计算方法。图18给出了不同温度、不同压力下高温接触热阻的变化规律。

图18 HTA-C与ZrB2-SiC材料间接触热阻预测[41]Fig.18 Prediction of contact thermal resistance between HTA-C and ZrB2-SiC[41]
赵建宁等[42-43]建立了基于多点接触的高温界面间断模型,研究获取了高温间断效应的形成演化机制和影响规律;构建了高效分析局部间断传热和力/热耦合问题的间断有限元(DG)方法,突破了间断问题分析中兼顾精度和效率等的方法瓶颈。图19[42]给出了某一维间断问题分析中DG与CG计算效率的对比结果。在此基础上,进一步发展了分区耦合的间断/连续伽辽金混合有限元(DG/CG)方法,形成了适应于复杂工程大规模计算的高效安全评估能力。图20[43]展示了基于DG/CG的疏导式防热结构热/力耦合分析结果。
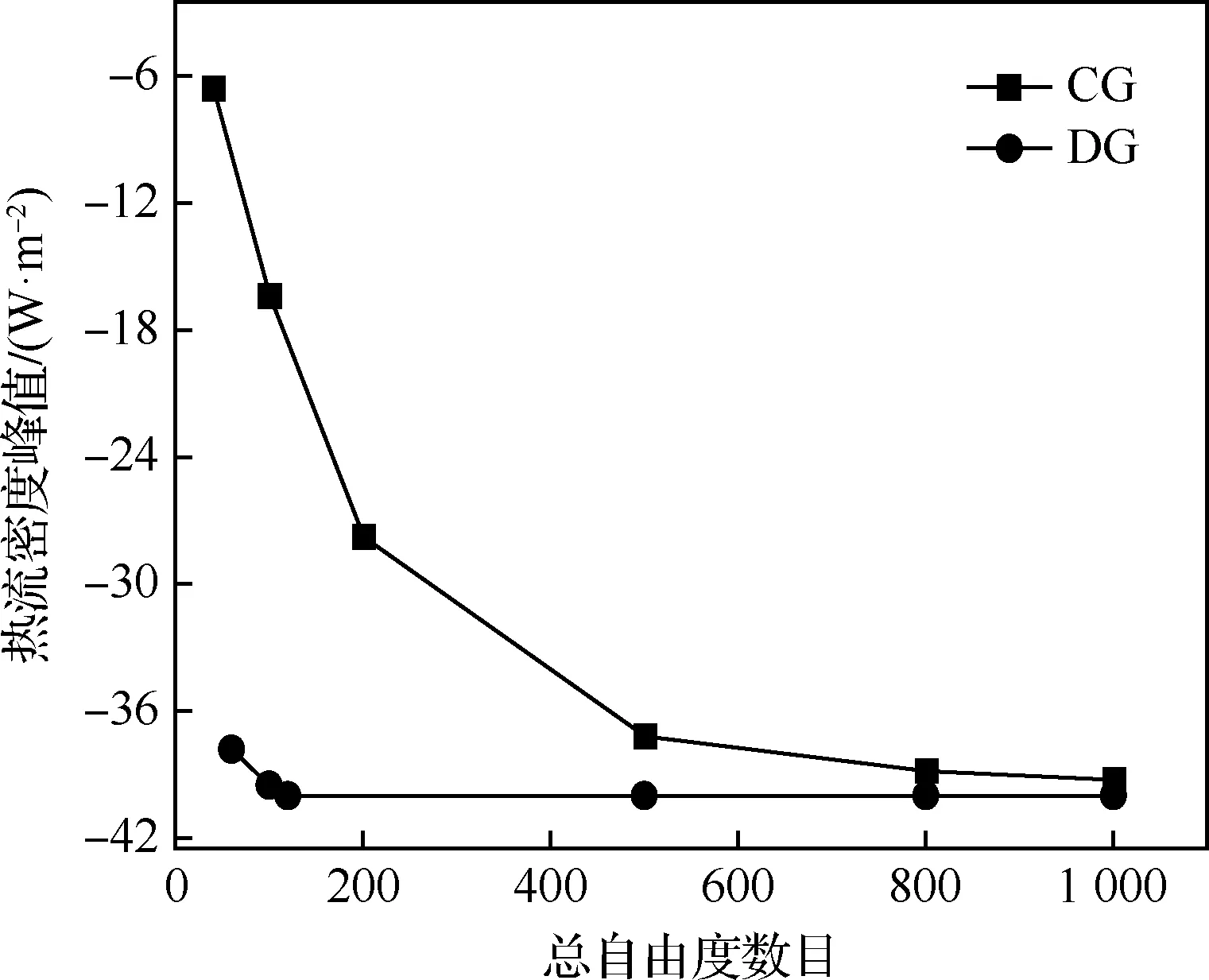
图19 某一维间断问题分析中DG与CG计算效率对比[42]Fig.19 Comparison of calculation efficiency of DG and CG for 1D discontinuity problem[42]
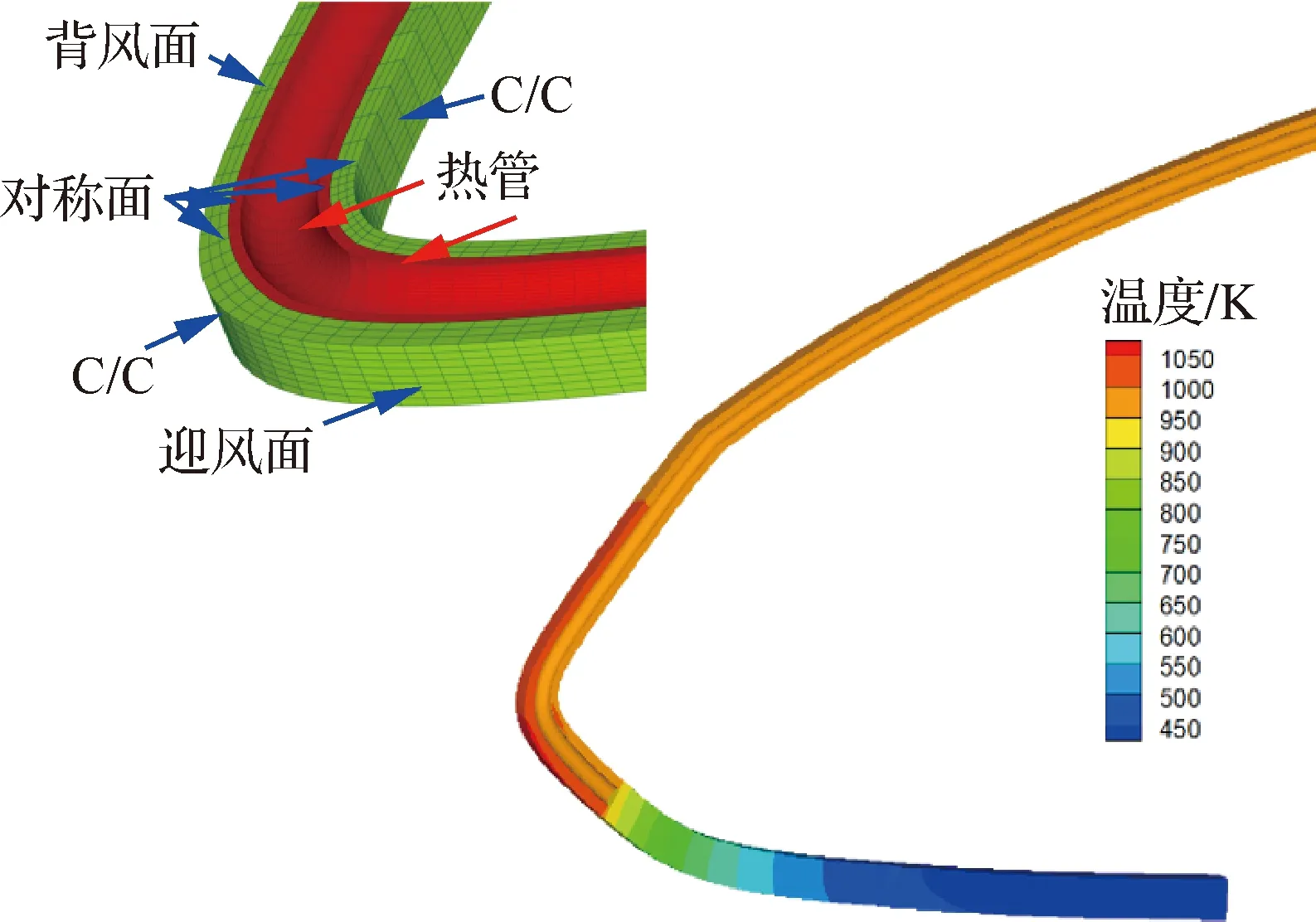
图20 基于DG/CG的疏导式防热结构热/力耦合分析[43]Fig.20 DG/CG based thermal mechanical coupled analysis of dredging thermal protection structure[43]
2.4 热气动弹性预测模型
长时间气动力/热综合作用下的热气动弹性问题给未来高超声速飞行器的热安全带来了前所未有的挑战[44]。为满足工程化应用需求,飞行器热气动弹性计算不仅需要准确计算单个物理场,还要考虑各个物理场之间的耦合效应,给数值模拟手段的计算精度与效率均提出了巨大挑战。
张伟伟等[45]发展了基于时空双向耦合策略的高效热气动弹性计算方法,构建了可适应于结构受热引发时变热模态的高超声速非定常气动力模型。图21[45]为适用于时变热模态的气动力降阶模型示意图及其与传统CFD结果对比。结果表明,该方法突破了结构模态随时间变化,以及材料热/力学特性随温度变化条件下非定常气动力高效重建这一瓶颈问题,大幅度提升了全耦合热气动弹性预测方法的工程实用性。
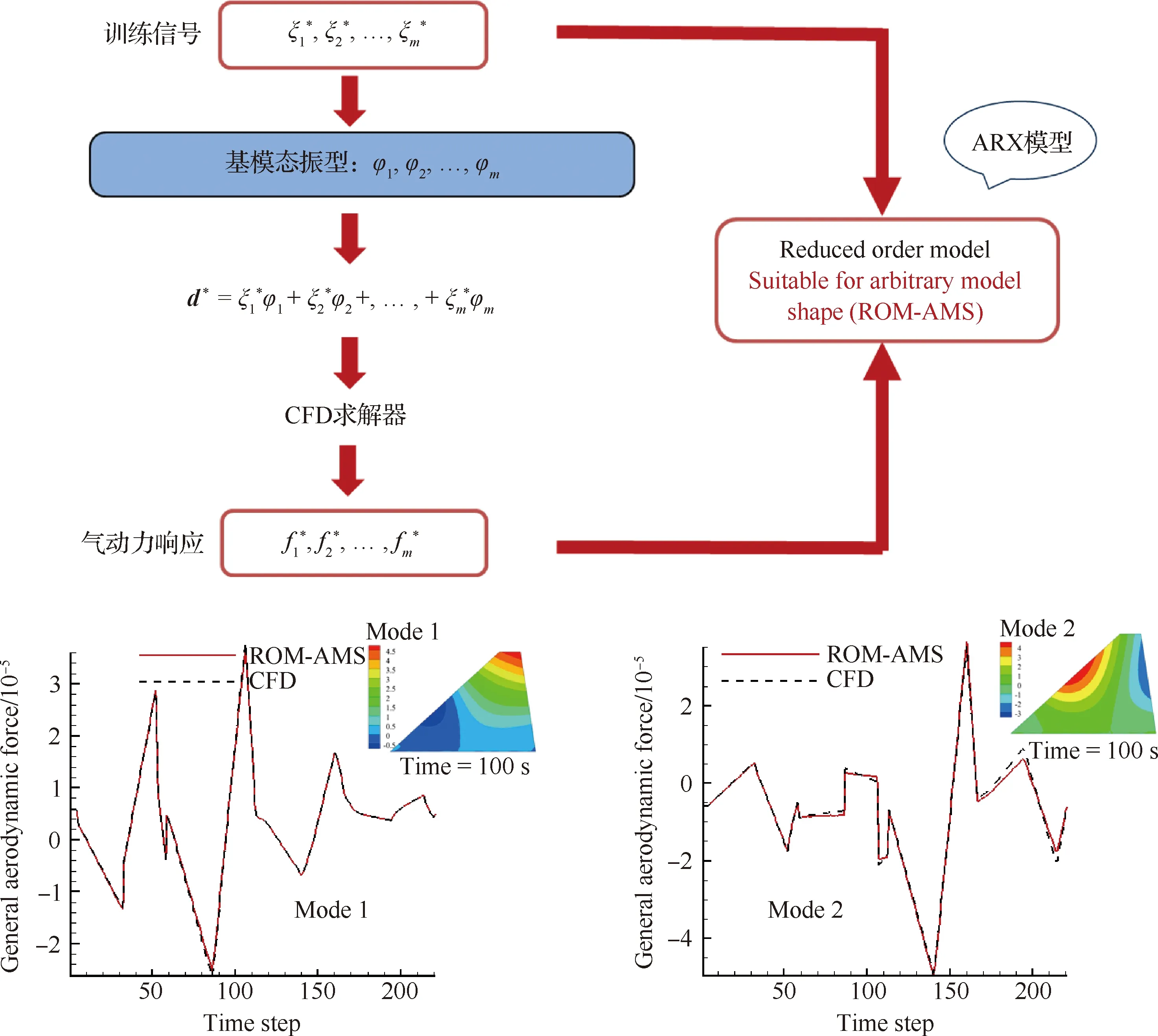
图21 适用于时变热模态的气动力降阶模型及其与传统CFD结果对比[45]Fig.21 Aerodynamic reduced order model for time-varying thermal modes and comparison between its results and CFD results[45]
3 多物理场耦合计算模型与方法
高超声速飞行器周围的气体流动存在稀薄效应、湍流效应、催化效应、烧蚀效应、辐射效应、非平衡效应等复杂的物理现象与化学反应,这些效应相互关联,耦合发生,在空气动力学上统称为多物理场。多物理场耦合问题的研究是模拟高超声速飞行器真实飞行状态的关键技术基础。NNW工程根据各自关注问题的侧重,开展了不同的物理模型和耦合方法研究。
3.1 高温近壁流动与材料表面催化烧蚀
在高温近壁流动方面,刘朋欣[46]、吴正园[47]等开展了高温化学非平衡湍流边界层直接数值模拟研究。刘朋欣等采用完全气体模型和高温空气化学反应模型对比了高超声速楔形体头激波后的流动状态,图22[46]给出了平板边界层瞬时流场的旋涡结构图,分析了化学非平衡效应对湍流统计量、湍流脉动量的影响趋势,并分析了边界层标度律,从图23[46]可以看出,Van Driest变换后的速度分布趋于一致。吴正园等对高温气体效应与湍流的耦合作用机理进行了分析,研究表明,高温气体效应使边界层内平均温度显著降低,平均密度显著升高,壁面平均压强和脉动压强均增加。
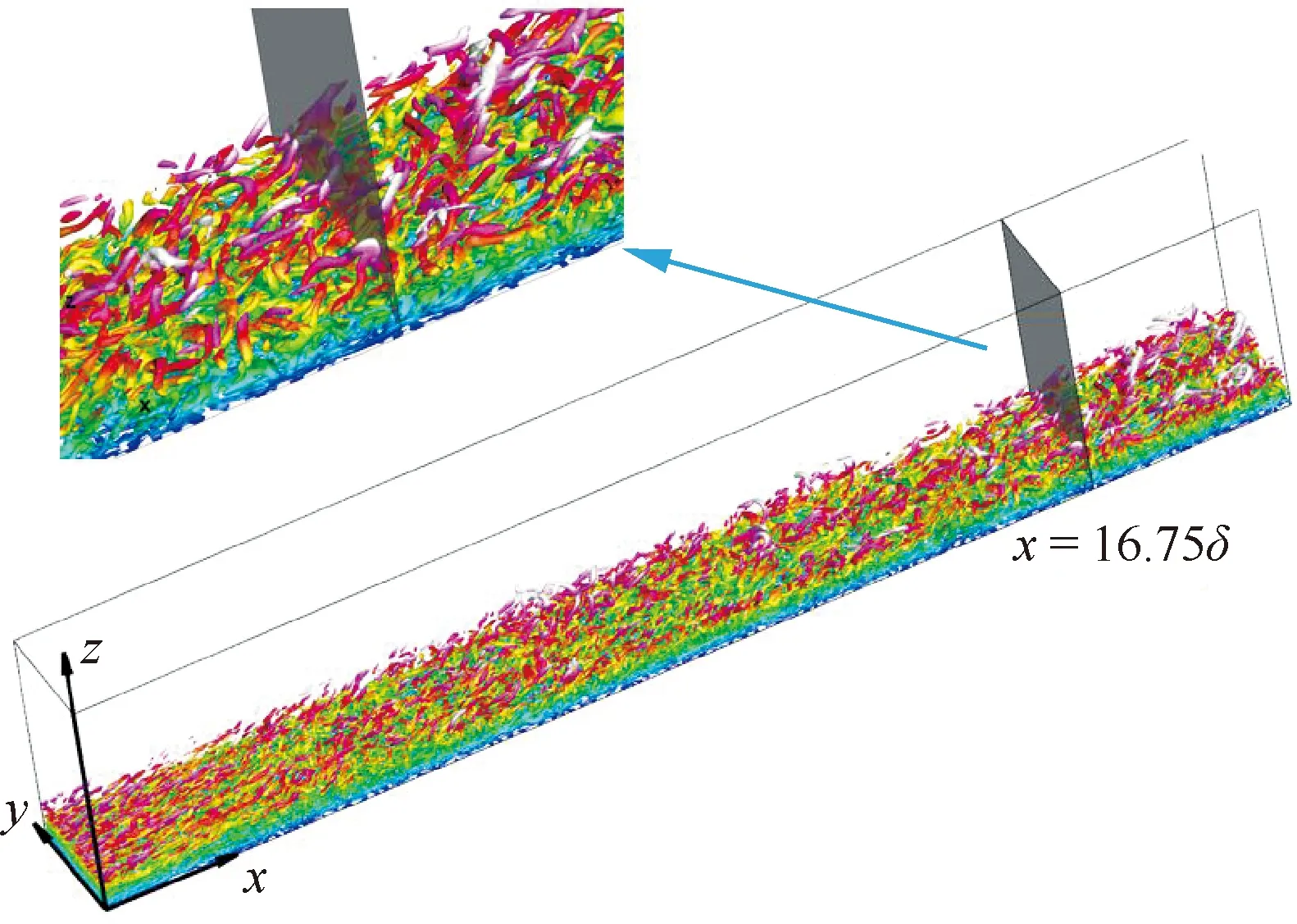
图22 Multi算例瞬时流场旋涡结构图(Qcr=0.05,法向高度着色)[46]Fig.22 Instantaneous vortex structures in Multi case(Qcr=0.05, colored by normal height)[46]
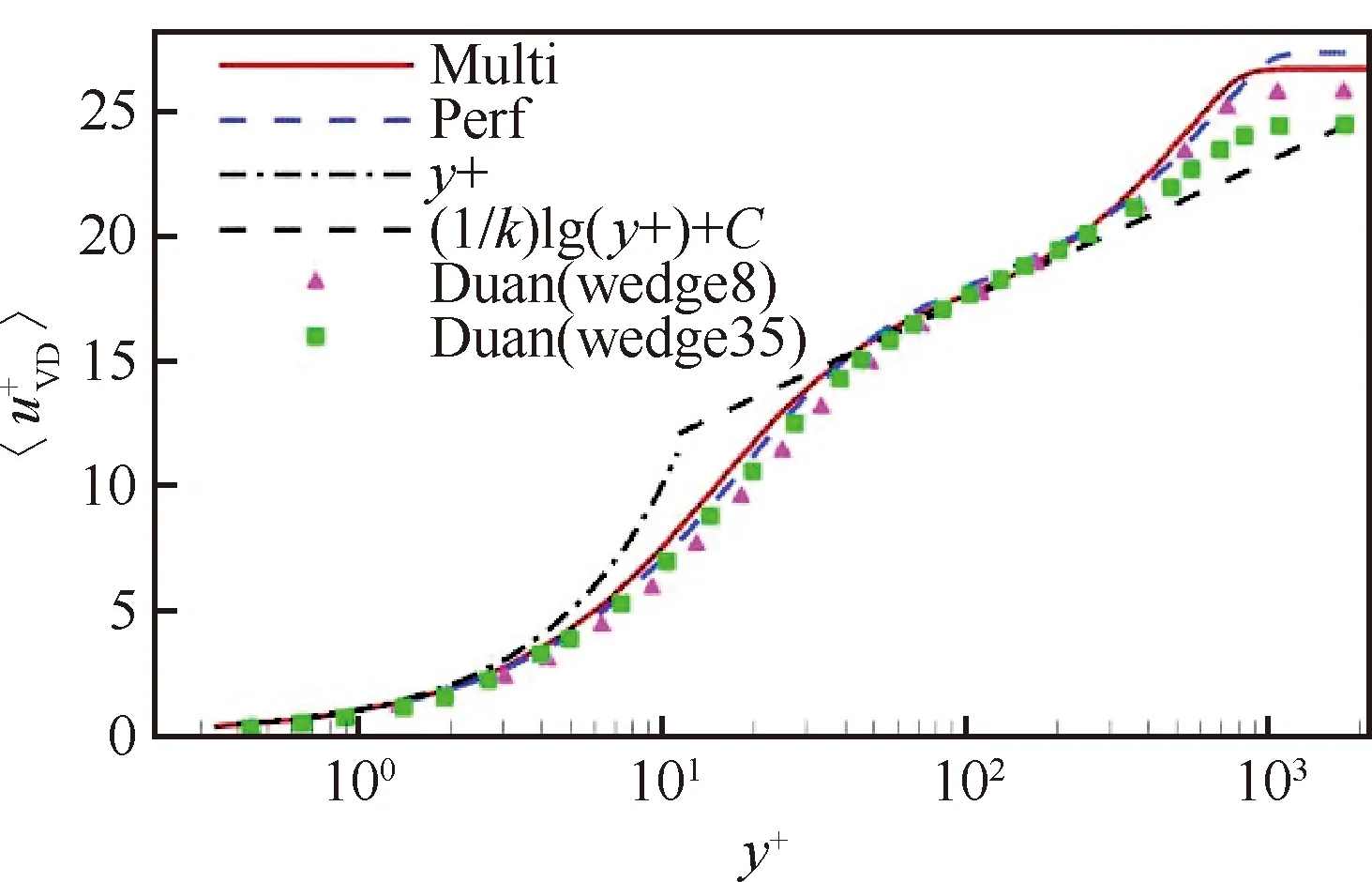
图23 Van Driest 变换后的速度分布[46]Fig.23 Profile of Van Driest transformed velocity[46]
李佳伟等[48]针对高超声速进气道前缘“Ⅳ型”激波干扰产生的气动加热与结构传热多物理场耦合计算问题,发展了一种基于有限体积法的流-热-固一体化计算方法,并提出了一种新的双温阻模型。该方法可以高效解决流场与结构传热稳态求解问题,较快计算出稳态结构与流场的温度分布。计算结果表明,“Ⅳ型”激波干扰作用会大大增加壁面最大压力系数和热流系数,对高速飞行器的热防护性能提出了更高的要求。
针对典型表面材料的催化/烧蚀特性以及与流场的耦合作用问题,崔志亮等[49]采用分子动力学模拟 MD 方法结合 ReaxFF 反应势函数,研究了高焓氧原子与碳基材料碰撞过程中发生的表面催化烧蚀过程及机理,探究了氧原子能流密度、石墨烯堆叠层数以及不同石墨表面晶型结构的影响。
磁流体控制与应用是空气动力学与电磁学相结合的内容,目前对耦合电磁场的高超声速流动机理的认识并不透彻。丁明松等[50]研究了高温气体效应对高超声速磁流体控制效率的影响,在低雷诺数下耦合求解了带电磁源项的三维N-S流场控制方程和电场泊松方程,对比分析了不同气体模型对磁流体控制的影响。研究表明,高温气体效应会极大地降低磁控增阻效果,会明显地增强部分表面区域的磁控热流减缓效果。
针对霍尔效应对高超声速磁流体力学控制的影响问题,丁明松等[51]耦合求解各向异性霍尔电场泊松方程和带电磁源项的高温热化学非平衡流动控制方程组,建立了高超声速流动磁流体力学控制霍尔效应数值模拟方法。图24[51]给出了环形电流密度的分布情况,计算结果表明,霍尔效应能改变洛伦兹力在等离子体中的分布,降低整体的磁控增阻特性;霍尔效应对高超声速 MHD 控制的影响,与壁面导电性和壁面附近漏电层的“漏电”现象紧密相关。
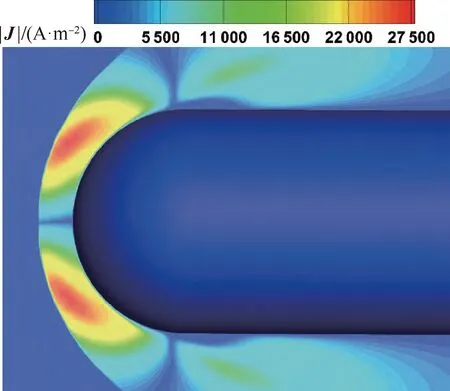
图24 环形电流密度大小[51]Fig.24 Density of annular electric current[51]
3.2 稀薄过渡流计算模型与方法
在跨流域飞行复杂流动方面,基于Navier-Stokes方程的CFD方法虽然有较高的计算效率,但对稀薄流动问题的物理描述不准确,亟需探索跨流域复杂流动问题的新型数值仿真模拟方法。
钟诚文团队[52-54]发展了计算高效、模型精确的确定论和统计论两套跨流域多尺度高效数值方法。在确定论方面,提出了非结构速度空间技术并发展了相应的积分补偿策略,空腔流动三维速度空间网格如图25所示[54];发展了双原子分子气体的全流域守恒隐式算法和多重隐式算法,提高了宏观量的预测精度和计算效率。
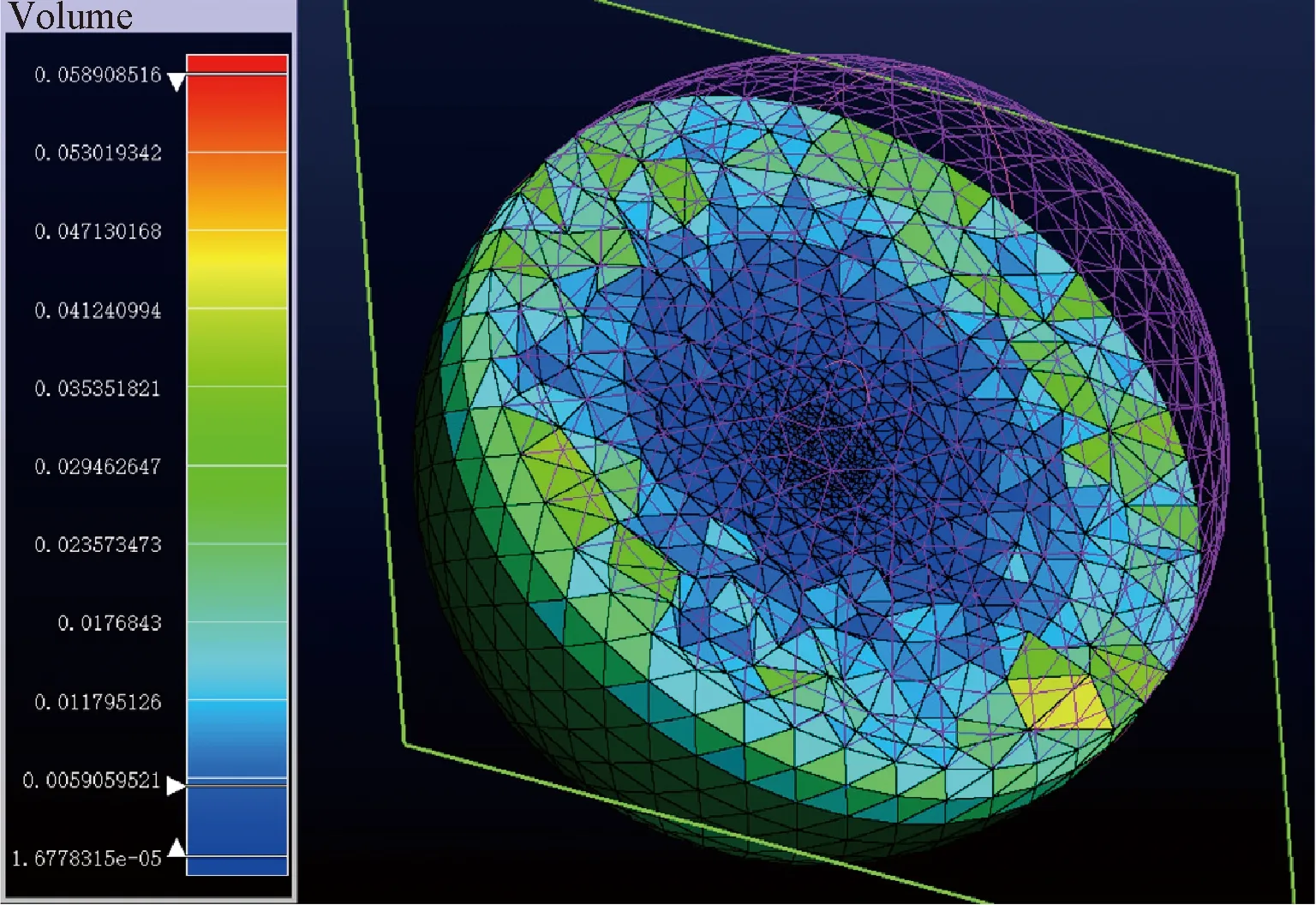
图25 空腔流动三维速度空间网格(49 950个网格)[54]Fig.25 3D velocity space mesh for cavity flow (49 950 cells)[54]
在统计论方面,钟诚文团队[55]发展了二维非结构网格下UGKWP (Unified Gas-Kinetic Wave-Particle) 算法,实现了非结构网格下波粒机制的耦合及多尺度计算,并验证了该方法在非结构网格下对全流域流动的模拟能力,在连续区能够还原为N-S方法。
费飞等[56-57]提出了基于BGK模型的多尺度随机粒子方法,比较了DSMC、BGK、FPM 3种方法中黏性系数与时间步长的关系(图26[57]),提高了随机粒子方法在连续流区域的计算精度,进一步扩展了随机粒子方法在跨流域流动中的计算能力。
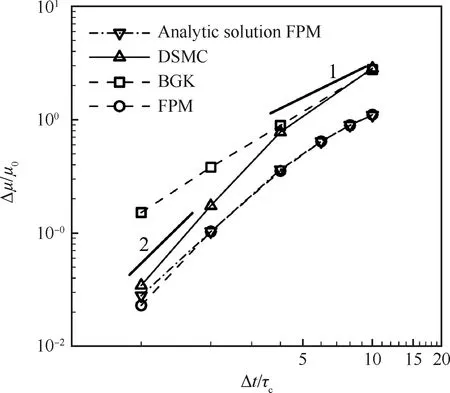
图26 DSMC、BGK、FPM 方法黏性系数与时间步长的关系[57]Fig.26 Relation of viscosity and time step for DSMC, BGK and FPM methods[57]
赵文文等[58]提出了一种改进的NCCR+ (Nonlinear Coupled Constitutive Relationsl) 模型,该模型具有模拟中等努森数非平衡高超声速流动压缩区和膨胀区的潜力。李廷伟等[59]针对统一气体动理论方法计算效率低的问题,采用数据驱动的思想,发展了一种稀薄非平衡流非线性本构关系求解方法。结果表明,该方法可同时提高计算效率和计算精度,应用潜力较高。
方明等[60]发展了一种采用组分追踪加权因子方法的DSMC模型,并将其应用于考虑稀有气体电离效应的三维复杂外形再入飞行器绕流计算,计算结果与飞行测量数据具有很好的一致性。
4 高阶精度数值计算方法
高精度数值计算方法在精度、分辨率等方面与传统方法相比有明显的优势,在复杂非定常、多尺度问题大规模精细模拟方面展现出很强的发展潜力,有助于提高NNW流场解算软件的精确性。然而,高精度方法在鲁棒性和高效计算方面仍然有很大的改进空间,有必要进行持续深入的研究。
4.1 结构网格高精度算法
高精度有限差分(Finite Difference)是最为常用的一类结构网格网精度算法,其中代表性的有WENO类格式等。随着工程上对高速流动的关注度越来越高,构造混合格式成为了有限差分方法的发展趋势。郭启龙等[61]在加权格式的算法框架上提出了一种基于特征变量的间断识别因子,并通过引入归一化函数极大地消除了间断识别因子的问题相关性,基于这种间断识别方法,可以构造出既能稳定捕捉激波又具有较低耗散的混合格式。相关算法已成功应用于转捩控制、湍流边界层DNS等[62-63]复杂流动研究中(图27)。随后,李辰等[64]将以上间断识别算法扩展到更窄的四点模板格式,通过降低模板的宽度有效增加了格式的鲁棒性。针对复杂外形模拟需求,李辰等[65-66]基于NND格式的模板,通过引入非线性加权和光滑度量因子改进,提出了WNND、WENO-L两种面向实际工程应用的高精度有限差分格式。
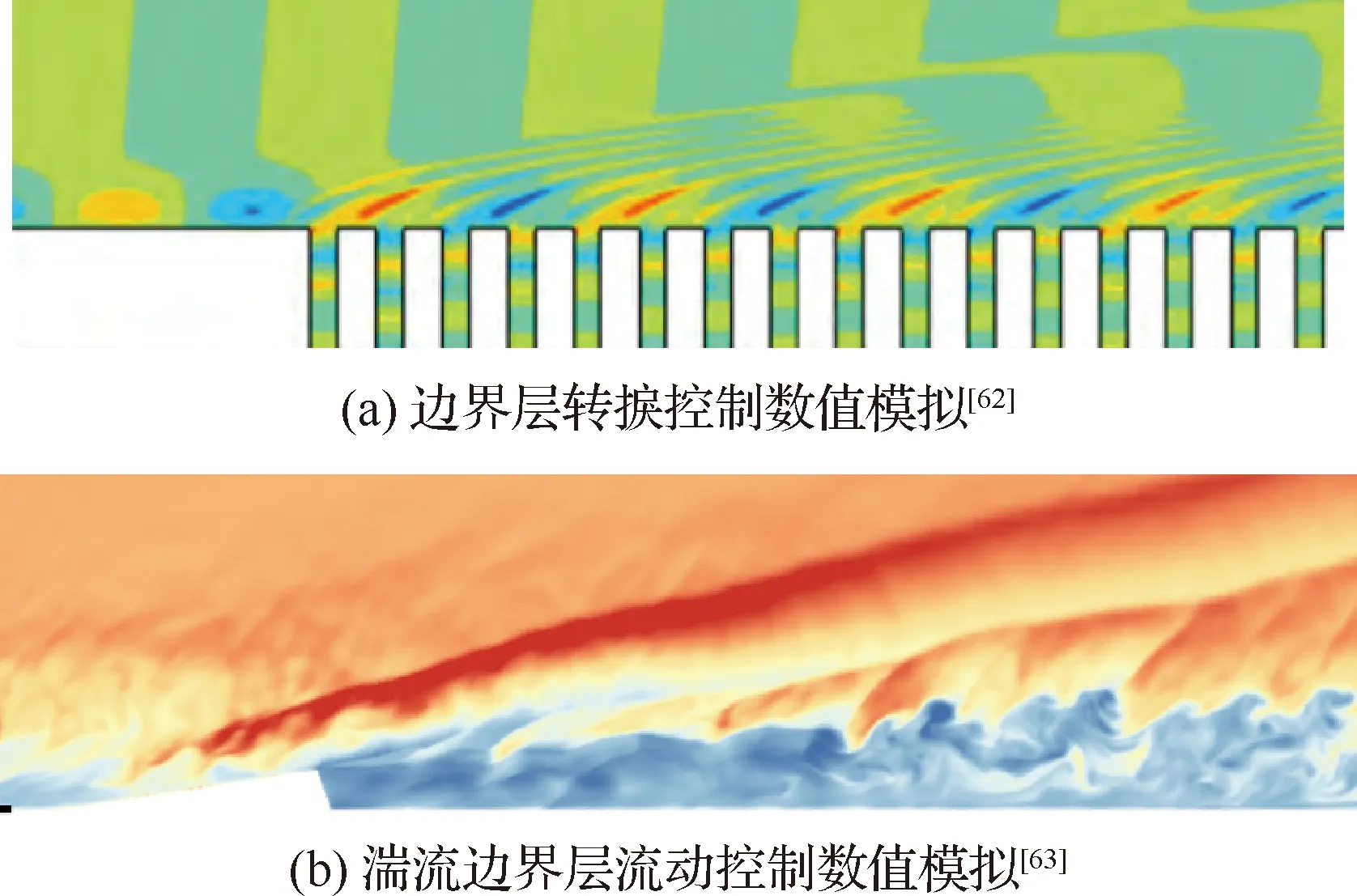
图27 高精度混合格式的应用Fig.27 Applications of high-order hybrid scheme
文献[67-69]基于对WENO格式光滑因子的分析,提出了对正弦函数为常数的光滑因子设计准则,基于该准则给出了一个光滑因子通用公式,并构造了七阶WENO格式及更高阶的WENO格式。新光滑因子在流场连续区域变化小而在间断附近变化大,且形式更简单,图28[67]中显示了一维间断附近不同光滑因子得到的最大值与最小值之比分布,其中新光滑因子(图中WENO7-S)的比值相比原始WENO7-JS结果高近2个量级,因此能为格式带来更好的间断稳定性。该系列WENO格式与其线性格式具有同样的近似色散关系,且同时具有计算量小、间断稳定性好和分辨率高的优势。

图28 间断附近各点通量计算中最大最小光滑因子的比值[67]Fig.28 Quotients of the largest smoothness indicator divided by the smallest one of every flux near discontinuities[67]
基于高阶精度基于重构的修正过程(Correction Procedure via Reconstruction, CPR)计算方法,朱华君等[70]利用与有限差分混合的方法,构造了具有强激波捕捉能力的计算方法,结合了两种方法的优势,显著提高了这类高阶精度计算方法在高超声速流动中的鲁棒性和应用能力,图29给出了该方法在极高Mach数问题计算中得到的密度云图。
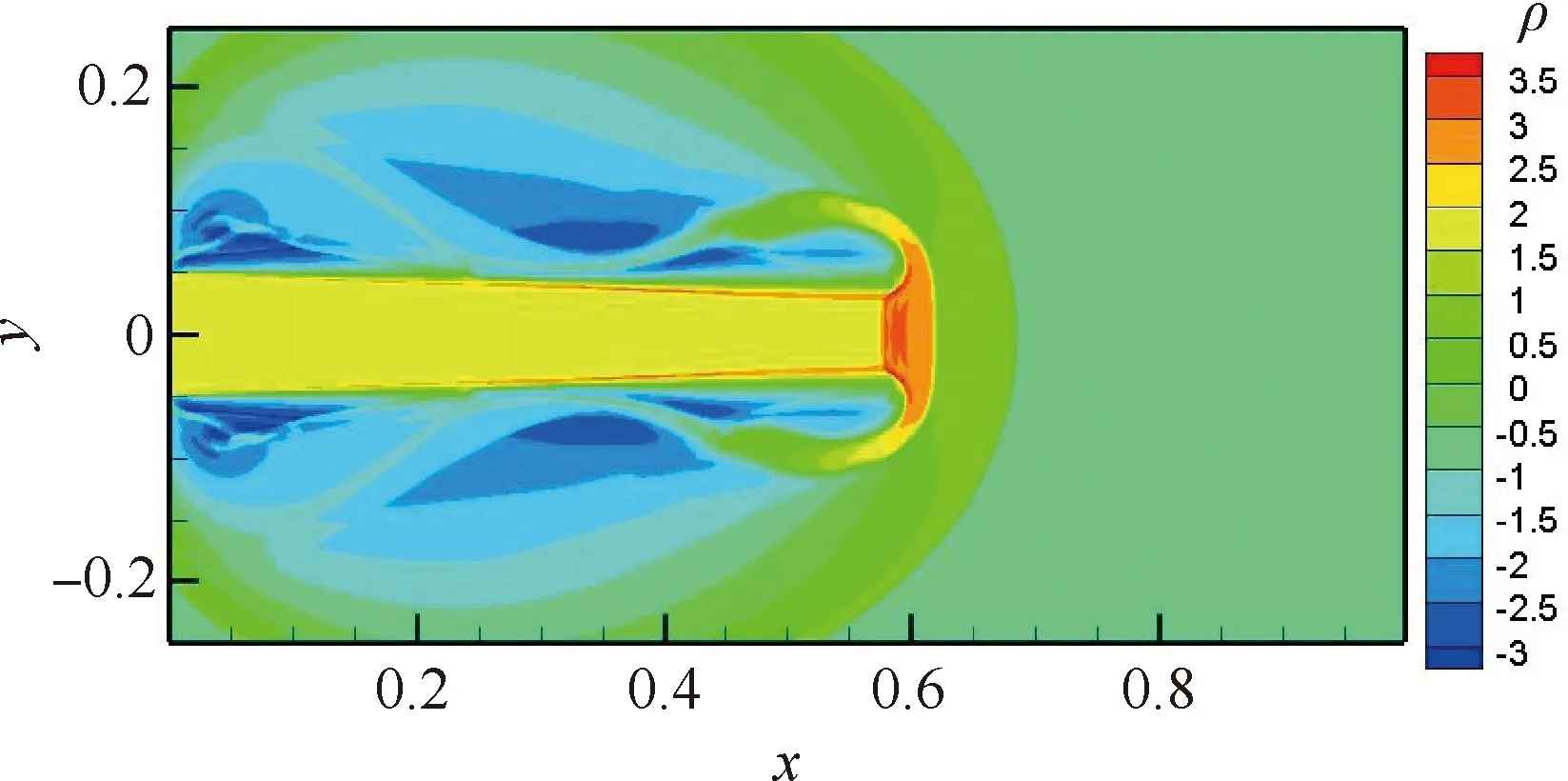
图29 强激波捕捉高阶精度CPR计算极高Mach数问题密度云图[70]Fig.29 Density distribution of extremely high Mach number problem using high-order CPR method[70]
4.2 非结构网格高精度算法
邵帅[71]发展了用于非结构DG方法黏性项离散的直接间断有限元方法(DDG),并将其推广应用于高阶精度DG/FV混合方法中。研究表明DDG方法相比传统DG黏性项离散的BR2方法具有单步计算量少,计算收敛所需步数少等优点。典型旋成体低速层流绕流算例三阶精度DDG-DG1/FV2相比BR2-DG1/FV2计算效率可以提高1.7倍,相比三阶BR2-DGP2计算效率可以提高4.3倍(图30)。

图30 旋成体标准算例密度残值收敛曲线[71]Fig.30 Density residual convergence of laminar flow over a body of revolution[71]
龚小权等[72]研究了基于精确雅可比矩阵计算技术的GMRES隐式方法。研究表明基于左端项Jacobi矩阵精确求解的GMRES计算效率相比Jacobi矩阵近似求解的GMRES和LU-SGS具有明显优势,典型亚声速无黏ONEAR-M6算例(DG四阶精度,马赫数为0.4,0°攻角,300万自由度)计算效率可提高一个数量级以上(图31)。
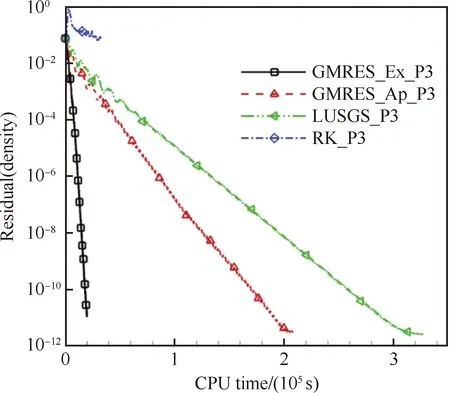
图31 ONERA-M6机翼DG(P3)的密度残值收敛曲线[72]Fig.31 Density residual convergence history of DG(P3) for ONERA-M6 wing[72]
燕振国等[73]基于非结构高阶精度算法,发展了一种新的预处理策略,并由此构建了高效隐式时间推进方法,显著提高了大规模非定常模拟的计算效率,且提高了非结构高阶精度方法在湍流高保真模拟等领域的模拟能力,图32展示了该方法在湍流圆柱绕流问题中计算得到的旋结构。

图32 非结构高阶精度算法湍流圆柱绕流计算网格和旋涡结构[73]Fig.32 Computational mesh and vortex structures of turbulent circular cylinder simulations using unstructured high-order methods[73]
任玉新等[74-75]基于前期提出的结构/非结构高精度算法理论框架,建立了不低于三阶空间精度的紧致有限体积算法,其中涵盖了保精度限制器、高效时间推进方法、高阶网格算法、高精度边界处理方法等,保证了算法的分辨率、计算效率以及鲁棒性。
文献[76-80]针对DDG方法中的激波捕捉问题提出了一种基于强残差的人工黏性技术,能够捕获激波,且隐式算法可以收敛到机器误差。同时设计了一种基于本地矩阵存储的隐式MPI并行算法,在二维、三维算例的测试中,计算效率提升了5%~10%,并且保证了千核并行效率在90%以上。
5 总结与展望
本文总结了NNW工程在CFD基础科学问题研究工作上的主要进展:在转捩与湍流模型及计算方法方面,发展了C-γ-Reθ转捩模型,改进了eN方法的三维转捩预测能力,建立了基于人工神经网络的大涡模拟模型等;在多相多介质计算模型与方法方面,发展了空间变光滑长度SPH方法和多自由度流固耦合模型,发展了ES-FEM-SPH方法,建立了表面效应的CFD/RMD耦合计算方法等;在多物理场耦合计算模型与方法方面,发展了基于有限体积法的流-热-固一体化计算方法,提出了基于BGK模型的多尺度随机粒子方法等;在高阶精度数值计算方法方面,构造了高精度混合有限差分格式,发展了新型DDG/FV格式等。
展望未来,NNW工程基础研究系统将在国内各参研团队的共同努力下,结合软件推广及实际应用中的基础理论及关键技术瓶颈问题,持续开展深入研究,以期进一步扩展国产CFD软件的能力边界。具体来说,各个重点方向的发展思路为:
1) 面向转捩与湍流,DNS能力边界将随着计算机性能的发展而大幅拓展,需要着力发展配套异构设备的高效高分辨率时空算法等技术;(隐式)大涡模拟、RANS-LES混合模拟将成为工程应用的主流,并需突破“灰区”抑制、近壁模型等关键技术。
2) 面向多相多介质流动,将更多地涉及微观/介观尺度的数值方法;同时需要进一步建立针对流/固界面大变形的非线性、不同相态转变等非平衡问题的计算模型与方法。
3) 面向多物理场耦合流动,需要考虑耦合的物理过程逐步增多,需要建立能够表征3种甚至4种物理过程的“耦合”的计算模型,重点涉及高温非平衡、气动噪声、电磁流等。
4) 面向高精度算法,主要解决实用范围扩展、鲁棒性不满足工程实用的难题,如基于非结构网格满足保正、保单调、能量/熵稳定的高精度算法;此外,针对各种极端流动条件下的高精度算法也是需要重点研究的方向。
致 谢
感谢中国空气动力研究与发展中心刘朋欣、李辰、向星皓、李明、燕振国、罗勇、李娜, 西北工业大学朱林阳, 中国科学技术大学黄生洪、薛正阳对本文的贡献。
