128m大跨度铁路应急钢桁梁极限荷载

2021-10-19陈士通孙志星许宏伟

中国铁道科学 2021年5期

赵曼，陈士通，孙志星，许宏伟

（1. 石家庄铁道大学土木工程学院，河北石家庄 050043；2. 石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室，河北石家庄 050043；3. 石家庄铁道大学河北省交通应急保障工程技术研究中心，河北石家庄 050043）

应急抢修钢梁主要用于自然灾害或战时桥梁损毁后的应急抢通，可反复拆装使用。应急使用过程中可能出现通行荷载不明确以及因碰撞、炸弹等外力导致构件局部损伤的现象，极限荷载分析是确保应急抢修钢梁极端条件下安全应用的前提。应急抢修钢梁多采用桁架结构，超载或杆件损伤易导致桁架结构强度或稳定破坏，出现极限承载力不足的情况［1-2］。为确保大跨应急抢修钢桁梁在极端条件下的结构安全，需深入研究结构的极限荷载，明确其非损伤状态和损伤状态下的破坏荷载及失效形式。

桥梁的极限荷载是研究桥梁极限承载力的重要指标，是桥梁工程师最关心的问题之一，国内外很多学者对其进行了研究［3-7］。早期采用线弹性理论，以屈曲分析的1阶荷载系数作为结构失效的极限荷载，这种方法过高地估计了结构的极限承载力。随着计算机的日益发展和广泛应用，非线性有限元法逐渐成为结构极限荷载分析的重要工具。文献［8］根据连续介质力学基本理论，采用非线性有限元法，研究了钢桁梁柔性拱桥在不同加载情况下的极限承载力，结果表明桥梁局部变形失稳是影响整体极限承载力的重要因素。文献［9］以贵州鸭池河特大桥为背景，研究了超大跨混合梁斜拉桥在荷载作用下的塑性区发展过程和极限状态下的破坏机理。文献［10］分析了主跨550 m 中承式钢拱桥的极限承载力，给出了影响大跨度拱桥极限承载力的主要参数。文献［11］通过对比3 种荷载工况的线弹性承载力分析，并考虑结构几何非线性与材料非线性的影响，系统分析了大跨度铁路钢桁梁柔性拱桥的极限承载力。文献［12］采用纤维模型法推导了材料非线性梁单元刚度矩阵公式，分析了大跨度钢桁拱桥加载全过程的塑性区发展和应力重分布情况，探讨了布载方式、拱上建筑联合作用等多种因素对结构极限荷载的影响。文献［13］以东江大桥为工程背景，开展了双层钢桁梁桥的弹性屈曲、非线性屈曲、极限承载力及失效机理和影响因素等各方面的研究和探讨。文献［14］以跨度61.5 m 双线下承式系杆拱桥为例，采用MIDAS Civil 和OpenSEES 软件建立了该桥弹性和弹塑性有限元模型，分析了初始缺陷对极限承载力的影响。文献［15］针对赣江二桥双塔双索面结合梁斜拉桥，考虑结构几何非线性及材料非线性，利用ANSYS 建立了该桥的整体稳定性分析模型，求解了4 种不同工况的弹性屈曲系数和第二类稳定的极限荷载。

综上所述，目前关于桥梁极限荷载的研究主要集中于永久性桥梁，针对铁路应急钢桁梁的研究相对较少，尤其是大跨铁路应急抢修钢桁梁。铁路应急抢修钢梁的构造、荷载与永久性桥梁存在较大差异，为明确大跨应急钢桁梁的极限荷载，本文依托128 m 跨铁路应急抢修钢桁梁，建立结构的三维非线性有限元模型，通过对非损伤状态下钢桁梁的弹塑性全过程分析，研究大跨应急钢桁梁破坏过程，确定钢桁梁结构的薄弱环节，并分析不同损伤状态下结构极限荷载变化规律。

1 128 m 大跨度铁路应急钢桁梁结构概况

大跨度铁路应急钢桁梁可拼组为上承式、半穿式和穿式梁，适用于56～128 m 跨度铁路桥梁抢修。相同桁高和桁宽时，128 m 跨钢桁梁稳定性和承载力最弱，故以128 m 跨为例展开分析。主桁杆件采用Q460qD钢材，平纵联及桥面系采用Q420D钢材。主桁中心距6.5 m，桁高12 m，主桁杆件均采用H 型钢，腹杆布置方式为不设竖杆的X 型体系，节间长度6 m 为主，辅以4 m 节间，可实现以4 m 为模数的跨度调整，主桁结构如图1 所示。最大使用跨度时结构宽跨比约1/20，与规范允许值下限相近［16］，结构整体刚度较弱。本钢桁梁共有20 种基本构件，其中主桁弦杆有重型弦杆、中型弦杆、轻型弦杆、端弦杆、畸零弦杆和弦杆端头6种；腹杆系杆件有基本长斜杆、端斜杆、轻型短斜杆和畸零短斜杆4种。

图1 128 m跨钢桁梁主桁结构图（单位：m）

2 有限元模型

为实现大跨应急钢桁梁极限荷载的精确分析，考虑几何、材料非线性对结构极限荷载的影响，采用ANSYS 软件建立结构非线性有限元模型［17-18］，如图2 所示。钢桁梁杆件采用beam189 模拟，主桁各杆件采用整体节点联结，节点按刚结处理，考虑的设计荷载包括恒载和活载，活载采用东风4型机车随挂70 kN·m-1均载，如图3 所示。鉴于战时随挂车辆的不确定性，出于安全考虑，结构设计时按随挂均载长度大于桥长考虑。

图2 128 m跨应急钢桁梁有限元模型

图3 货物列车荷载

主桁杆件材料本构关系采用图4 所示双线性弹塑性模型，即材料经过弹性阶段达到屈服应力后，进入强化阶段，强度会有小幅度提升，强化系数取为0.5%。钢材属于各向同性材料，适宜采用Mises屈服准则作为评判结构破坏的标准。Mises 屈服准则可表示为

式中：σe为截面等效应力；σy为材料屈服应力。

图4 主桁杆件的材料本构关系

3 极限荷载

结构的极限荷载是指结构失效前所能承受的最大外荷载，结构失效形式通常表现为2 种：一是个别构件应力达到材料屈服强度的失效，属于强度破坏；二是结构整体失稳或个别构件失稳，属于稳定破坏［13，19］。在研究桥梁极限荷载时，将恒载视为常量，施加的外荷载与设计活载的相对比值定义为活载系数λ，结构破坏时的活载系数即为极限荷载系数λu。

在此对恒载和列车活载作用下，128 m 跨应急钢桁梁非损伤状态和损伤状态下的极限荷载进行探讨。

3.1 非损伤状态线弹性条件下的极限荷载

结构的极限荷载除了与材料特性、结构刚度和边界条件等有关外，还与荷载组合方式及活载布置形式密切相关。针对列车荷载，其在桥上运行过程中，列车位置时刻变化，即不同位置的列车荷载对桥梁作用不同，故对于桥梁而言，需探求列车位置对其极限荷载的影响，在此选择列车车头位于L/8，L/4，L/2，3L/4，L，5L/4，3L/2，7L/4及2L（L为跨径）9 种工况进行线弹性分析，以确定结构最不利荷载工况。

图5 给出了列车荷载位于不同位置的极限荷载系数λu。由图5 可知：列车通过钢桁梁的过程中，极限荷载系数λu呈现先急剧下降、后缓慢下降再趋于稳定的变化规律。列车位于L/8 时，λu为17.071；位于L/2 时，λu为10.367；车头驶离钢桁梁后，λu为8.093，并保持不变。通过对λu的比较可确定，最不利荷载工况为车头驶离钢桁梁，随挂均载满布钢桁梁，故后续以此工况作为基本荷载进行分析。

图5 列车荷载不同位置时的极限荷载系数

3.2 非损伤状态弹塑性条件下的极限荷载

大跨桥梁的破坏常伴随发生大变形，并与材料非线性有着密切关系，因此考虑几何、材料双重非线性进行极限荷载分析。

3.2.1 钢桁梁竖向位移和等效应力纵向分布

非损伤状态下，不同活载系数λ时钢桁梁竖向位移的纵向分布如图6 所示。由图6 可知：活载系数λ不同时，位移分布曲线趋势基本一致，均呈现抛物线形，符合简支梁的受力特点。钢桁梁各处竖向位移随活载系数λ增大而增大，其中以跨中位移增大得最大。

图6 不同活载系数λ时竖向位移的纵向分布

图7 给出了不同活载系数λ时钢桁梁的等效应力的纵向分布。由图7 可见：钢桁梁两端应力较小，中间应力分布比较均匀，最大应力出现在跨中；λ=1时，最大应力为282.6 MPa，钢桁梁整体处于弹性阶段；λ=2.028 时，跨中杆件个别截面应力最先达到屈服应力460 MPa，是整个钢桁梁结构的控制杆件；λ=2.231 时，荷载达到极限值，中间区域杆件应力均达到屈服应力，并产生较大塑性变形；其他位置杆件受力相对较小，杆件发生较小塑性变形或依然处于弹性阶段，杆件距离跨中越远，安全富裕度越大；等效应力达到屈服应力杆件的位置范围约在34～94 m，说明钢桁梁破坏时，中间区域杆件基本上都处于屈服状态，材料性能得到了充分发挥；等效应力分布曲线呈锯齿状变化，这是由于平纵联杆件对主桁弦杆的横向作用，使得每根弦杆的应力分布不均匀；距离梁端40 m 左右处，杆件应力分布出现明显突变现象，其原因是该处为重型弦杆与中型弦杆分界点，不同类型杆件截面尺寸不同，引发截面应力突变，实际工程中，中型弦杆端部位置设有局部加强，而建模时未考虑杆件局部加强（偏于安全）所致。

图7 不同活载系数λ时等效应力的纵向分布

3.2.2 跨中竖向位移、应力和应变历程曲线

跨中杆件是整个钢桁梁结构的控制杆件，故选取跨中杆件进行历程分析。图8给出了不同活载系数λ下钢桁梁跨中杆件的竖向位移、等效应力和应变曲线。由图8 可知：λ=0（钢桁梁自重作用）时，跨中竖向位移为165.1 mm，截面应力为105 MPa，远低于屈服应力，此时结构中所有杆件均处于弹性阶段；λ=1（钢桁梁自重与活载共同作用）时，跨中位移为432.0 mm，截面应力为282.6 MPa，结构依然处于弹性应力状态；荷载逐渐增加至λ=2.028 时，跨中位移为710.6 mm，截面应力刚好达到屈服应力460 MPa，处于弹塑性变形的临界点；荷载继续增加，部分杆件开始屈服并发生塑性变形，且塑性应变随荷载增加迅速增大，塑性区范围以及屈服杆件的数量也随之快速增加，使得钢桁梁整体的竖向位移急剧增加，进而引发结构大变形；荷载增至λ=2.231 时，跨中位移为1 050.0 mm，钢桁梁因变形过大发生屈曲失稳，荷载和位移均达到最大值，钢桁梁处于极限状态，完全丧失抵抗更大荷载的能力。

图8 不同活载系数λ 下跨中杆件的竖向位移、等效应力和应变曲线

通过以上对跨中杆件的分析可知：当活载系数λ从2.028 到2.231（增加10.01%）时，竖向位移从710.6 mm 变为1 050.0 mm（增加41.99%），总应变相比弹性应变则增加约20 倍。综合上述分析可确定λ=2.028 时的外荷载为屈服荷载，λ=2.231 时的外荷载为钢桁梁失稳破坏的极限荷载，活载系数λ=2.231 即为钢桁梁的极限荷载系数λu。由于现行铁路桥规无相关规定，参考有关文献［20-22］规定“结构按弹塑性全过程分析时，安全系数可取为2.0”可知，非损伤状态下钢桁梁具有足够的安全保证。

3.3 杆件损伤状态下的极限荷载

应急钢桁梁使用过程中可能因外力导致构件损伤，构件损伤具有不确定性。在此根据杆件损伤位置、损伤长度和损伤形式，构建不同损伤程度下的损伤工况进行分析。

3.3.1 不同损伤位置的极限荷载

根据钢桁梁受力特点和结构特点，选择3 个损伤位置：L/4，3L/8 和L/2，损伤长度取为单位长度1 m，损伤形式为截面尺寸减小，用面积折减系数ζA模拟杆件截面损伤程度，分析时依次取ζA为1.00，0.95，0.90，0.85和0.80。

图9 给出了不同损伤位置时钢桁梁的极限荷载系数。由图9 可知：损伤位置在L/4 时，λu随损伤程度基本不变；损伤位置在L/2 时，λu随损伤程度增加而迅速减小；损伤位置在3L/8 时，λu的变化趋势则介于损伤位置在L/4 和L/2 之间。这是由于简支钢桁梁跨中杆件受力最为不利，是整个结构的控制杆件，故跨中杆件损伤对钢桁梁极限荷载影响最大，而其他位置的杆件为次要杆件，距离跨中越远，该处杆件的损伤对极限荷载影响越弱。由此可见，杆件损伤位置对钢桁梁极限荷载影响显著，损伤位置越靠近跨中，其影响越大。参考前述安全系数为2.0 的规定，当损伤位置位于L/4～3L/4 之间，ζA＜0.9时，极限荷载系数λu低于2.0，需及时采取加固或降载措施确保运营安全。

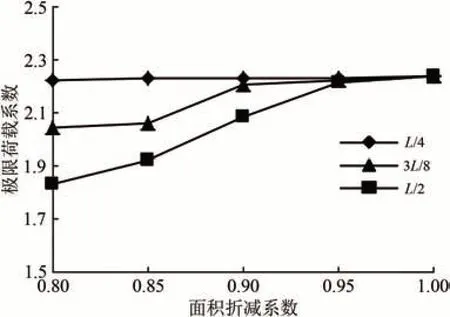
图9 不同损伤位置时的极限荷载系数λu

图10 给出了不同损伤位置时钢桁梁的极限位移。由图10 可知：杆件发生损伤后，极限位移都有不同程度减小，其中损伤位置在L/2时，极限位移下降速度最大；而损伤位置在L/4时，极限位移下降比较缓慢，主要是由于损伤位置对钢桁梁极限荷载的影响程度不同，且杆件损伤程度直接影响结构刚度和承载力，极限位移则必然随之递变。

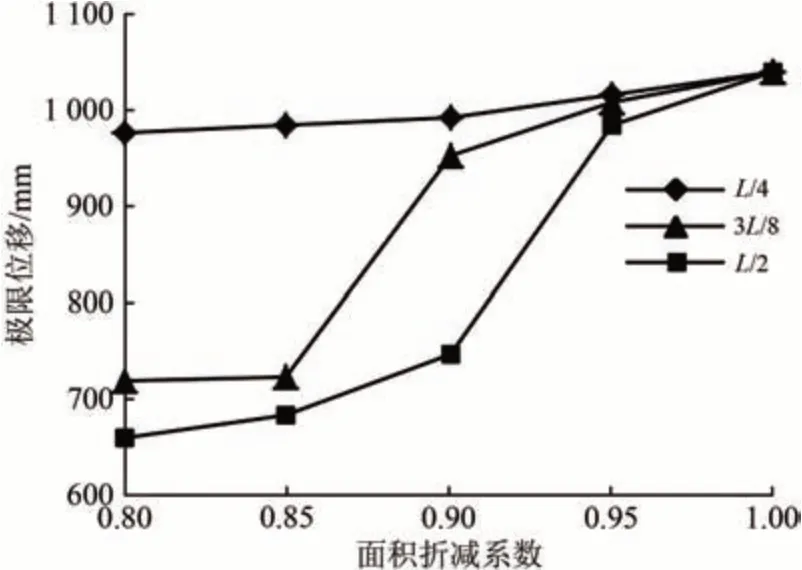
图10 不同损伤位置时的极限位移

图11 给出了不同损伤位置的位移-活载系数曲线。由图11 可见：截面损伤程度较小（ζA=0.95）时，不同损伤工况的跨中位移历程曲线变化趋势基本相似，破坏前都会产生较大变形，属于失稳破坏。截面损伤程度较大（ζA=0.85）时，不同损伤位置的荷载-位移曲线差别较大，损伤位置在L/4时，跨中极限位移为1 030 mm，虽然损伤程度较大，但是由于损伤位置在L/4处，杆件受力相对较小，对结构承载力影响较弱，故在此工况下，依然是跨中杆件控制结构承载力。而当损伤位置位于L/2 时，跨中极限位移只有680 mm，反映在位移历程曲线上是只有直线段，没有平缓段，说明结构破坏时没有发生明显大变形，其原因是跨中杆件损伤程度较大，截面尺寸明显减小，损伤区域是跨中杆件和整个钢桁梁结构的薄弱环节，在荷载作用下损伤区域首先达到屈服强度，同时因损伤杆件刚度锐减使得内力不能有效传递到其他尚处于弹性阶段的杆件，内力重分布效应减弱，因此损伤杆件会突然压溃，其失效形式是由于损伤构件自身承载面积不足引起的弹性阶段破坏，属于强度破坏，破坏前没有征兆，工程中应避免出现。

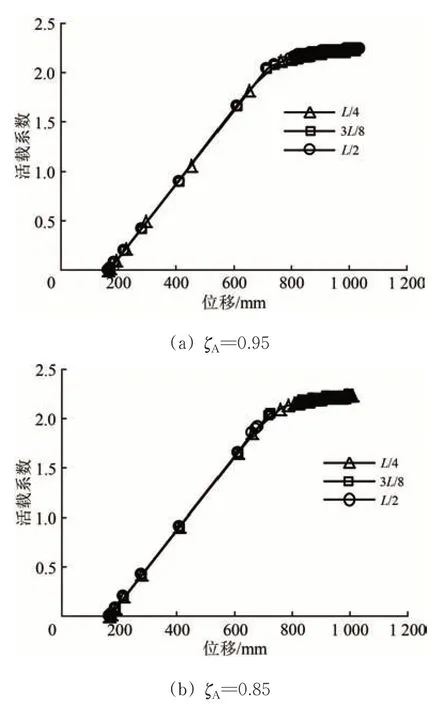
图11 不同损伤位置时的位移-活载系数曲线

3.3.2 不同损伤长度的极限荷载

为精确分析损伤长度对钢桁梁极限荷载的影响，需对杆件损伤单元的划分进行细化，其中非损伤单元长度为0.5 m，损伤单元长度为0.1 m。基于前面分析，选取损伤位置在跨中的工况进行极限荷载分析。

图12 给出了不同损伤长度的极限荷载系数。由图12 可知：跨中杆件损伤后，结构承载力会出现不同程度减小。损伤长度在0.6 m 左右时，极限荷载迅速减小，损伤程度越大，减小率越大，其原因是损伤长度较小时，损伤杆件的刚度减弱对内力影响较小，而对截面应力影响较大，结构因损伤杆件局部应力过大而发生强度破坏。损伤长度大约在0.6～3 m 之间时，极限荷载有小幅提高。这是因为杆件塑性区域随损伤长度增加而增加，有利于结构内力重分配，使得相邻未损伤区域的内力增加，而损伤区域的内力减小，其应力也随之减小，因此极限荷载会稍有增大。损伤长度≥3 m（1/2 节间长度）时，相同损伤程度下的极限荷载系数λu将趋于稳定，这是因为杆件屈服后的内力重分配范围有一定限制，极限荷载不再随损伤长度而变化。从损伤程度来看，极限荷载随损伤程度增加而减小，由于极限荷载降低，极限位移也随损伤程度增加而减小。综上所述，当杆件损伤长度≥3 m 时，不同损伤程度的结构极限荷载和极限位移不再随损伤长度而变化，而是分别趋于某稳定值。

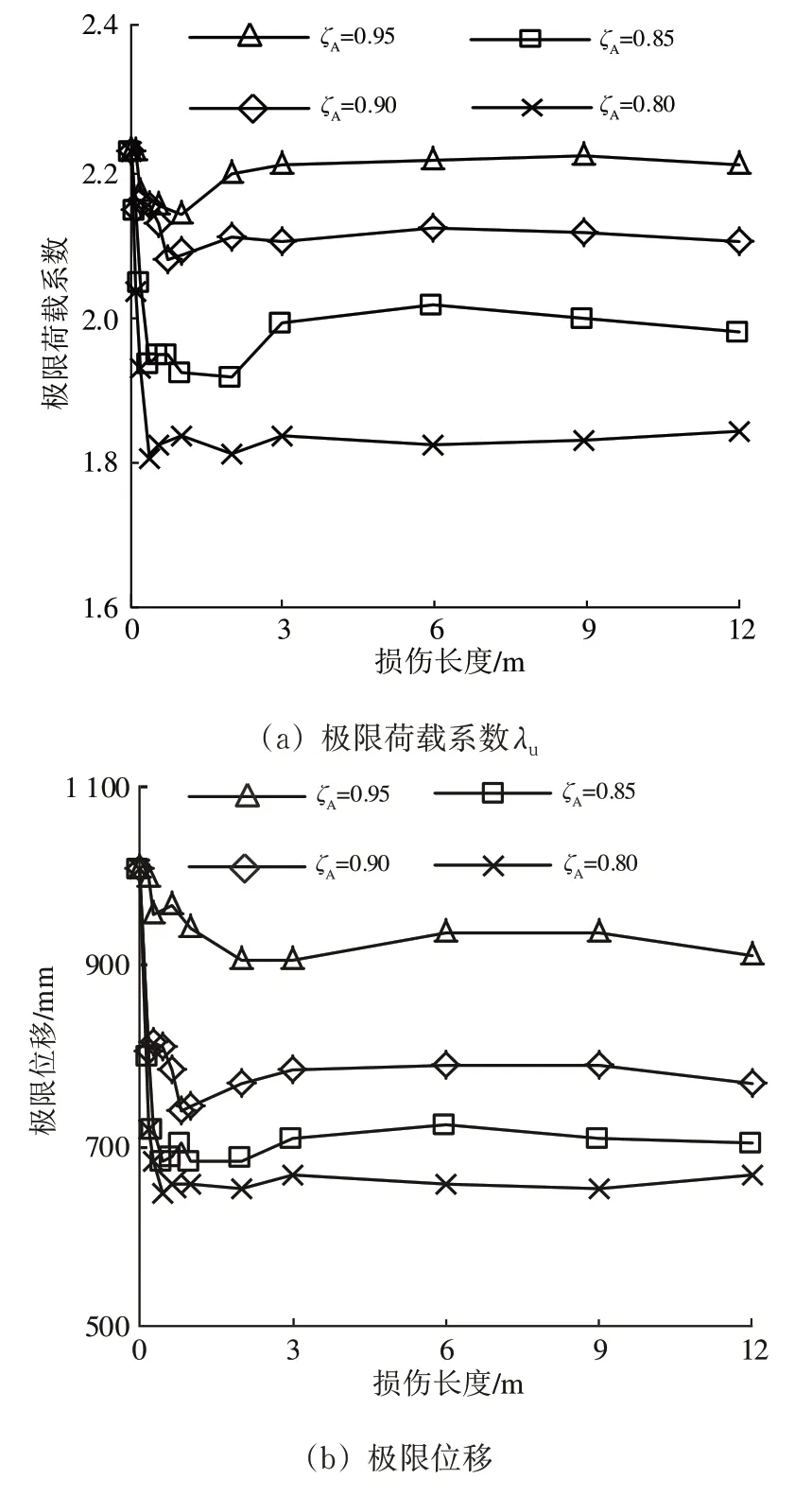
图12 不同损伤长度的极限荷载系数λu和极限位移

3.3.3 不同损伤形式的极限荷载

杆件损伤形式主要表现为：杆件截面尺寸减小、材料强度退化和材料刚度退化，分别对应杆件截面面积A、材料屈服强度σy和材料弹性模量E，相应折减系数可表示为ζA，ζσ，ζE。根据损伤长度对结构承载力的影响，下面对单点损伤和整杆损伤2种类型分别进行探讨。

单点损伤分析中损伤长度取单位长度1 m，损伤位置依然位于跨中。图13 给出了不同损伤形式的极限荷载系数λu和极限位移。由图13 可知：截面尺寸减小和材料强度退化引起的损伤对钢桁梁极限荷载影响显著，而材料弹性模量降低对钢桁梁极限荷载影响甚小。究其原因是杆件截面尺寸减小，使得相同荷载作用下截面应力增大，杆件提前进入塑性状态。同理，材料强度的退化意味着材料屈服应力降低，也会使杆件提前进入塑性状态。杆件屈服后，其刚度和抵抗外荷载的能力均随之降低，因此杆件截面尺寸减小和材料强度退化都会使钢桁梁极限荷载明显减小。而材料刚度退化对钢桁梁极限荷载影响很小，不同的弹模折减系数ζE时，极限荷载基本不变，主要是因为钢桁梁结构的最终破坏是因杆件达到屈服强度后发生大变形而失稳，而与材料弹性模量关系较小，因此不同刚度退化的极限荷载基本不变，但是刚度退化对极限位移有一定影响，弹性模量减小会使得结构抗变形能力降低，因此极限位移会随着刚度退化而稍有增加。当面积折减系数ζA和强度折减系数ζσ低于0.90 时，结构极限荷载系数λu小于2.0，同样需要降载通行或采取加固措施，杆件加固时需注意钢材材质，所用钢材屈服强度不宜低于原材料屈服强度，如材料筹集困难，可折算后通过增大杆件截面的形式予以临时加固，此外，利用不同材质钢材加固还需注意焊接工艺。

图13 单点损伤时不同损伤形式的极限荷载系数λu和极限位移

整杆损伤分析中损伤长度取为1 个节间长度6 m，图14 给出了整杆损伤时不同损伤形式的极限荷载系数λu和极限位移。由图14 可知：与单点损伤相同，弹模降低对极限荷载和极限位移的影响很小；与单点损伤不同的是，相比于强度折减，面积折减对极限荷载系数λu和极限位移的影响更明显，主要原因是整根杆件截面尺寸的损伤，除了会降低杆件承载面积外，还会减小杆件截面惯性矩，加之结构破坏时大变形的影响，使偏心弯矩引起的弯曲应力加大，因此极限荷载降低最明显。

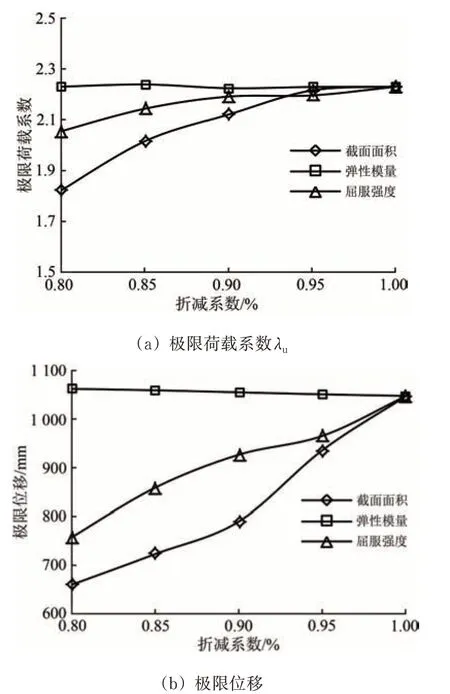
图14 整杆损伤时不同损伤形式的极限荷载系数λu和极限位移

综上所述，不论是单点损伤还是整杆损伤，不同损伤形式对钢桁梁极限荷载的影响差异较大，杆件截面损伤和材料强度退化对极限荷载的影响明显，而材料刚度退化的影响可基本忽略。

综合来看，钢桁梁中某杆件发生损伤后，相比非损伤状态，极限荷载都会有不同程度减小，但其减小率均小于杆件损伤率，究其原因是杆件损伤易引起杆件局部区域塑性变形和局部破坏，交汇于某一节点的单一杆件局部破坏后，将引起节点局部失衡，外力作用下，局部失衡损失的抗弯或抗剪刚度将向节点周围构件转移，引发内力重分布，并形成新的平衡系统。但随着外部荷载的增大，将有更多杆件进入塑性状态并逐渐发生破坏，最终导致整个桁梁结构不能继续承载而完全破坏。