基于HHT的地震作用下基覆型边坡坍塌特性研究

2021-10-19杨长卫童心豪蔡德钩瞿立明郭雪岩

中国铁道科学 2021年5期

杨长卫，童心豪，蔡德钩，张良，瞿立明，郭雪岩

（1. 西南交通大学土木工程学院，四川成都 610031；2. 中国铁道科学研究院集团有限公司铁道建筑研究所，北京 100081）

我国国土面积大，分布着数量众多的各类型边坡，复杂险峻的边坡对沿线交通、房屋及公共建筑造成了极大的威胁［1］，其中，边坡坍塌是边坡破坏的重要表现形式之一。近年来，边坡安全问题已成为工程领域内的热点研究，国内外学者对于边坡的滑坡、落石和坍塌等灾害发生机理方面已经有了丰硕的研究成果，对于边坡工程的防护也取得了极大的进展。地震是我国中西部地区频发的自然灾害，常导致边坡防护失效，我国汶川地震时就造成约3 万～5 万处山体滑坡、崩塌和碎屑流灾害，地震次生地质灾害造成遇难人数占总遇难人数的1/3［2］。坍塌是指坡面或边坡上覆土层发生一定规模变形而坡体尚未大面积变形的边坡变形形式，主要发生在堆积层或破碎岩层［3］，其发生可能性仅次于崩塌和滑坡［4］。

边坡坍塌常常与其他边坡灾害混淆，国内外许多学者将边坡坍塌归类于崩塌或滑坡之中，缺乏深入研究。边坡坍塌时坡体会出现部分塌陷或碎石掉落，导致下部结构遭受落石或滚木等突然性的小型冲击，但由于坍塌不会像崩塌或滑坡一样造成坡体整体位移，容易被人忽略其危害性。实际上，坍塌是边坡结构遭遇整体破坏的早期征兆，地震导致的边坡崩塌和滑坡也很可能是先发生边坡坍塌破坏再引起整体结构发生位移。

边坡破坏的内因有岩土体类型［5］、坡度等，外因有地震、降雨、地下水变化等，目前已有许多学者针对边坡破坏的相关原因进行了研究。Keefer［6］通过历史地震信息提出了地震滑坡分类方法，分析了滑坡与地震参数之间的关系；Hutchinson等［7］通过地面激光扫描测定了地震对岩石边坡的影响；Zhao 等［8］通过实地调查分析了九寨沟7.0级地震导致滑坡的破坏特点；郑静等［4，9］通过对汶川8.0 级地震现场调查分析了地震导致边坡破坏的形式和具体类型，发现坍塌主要发生在二元结构的边坡上，且坍塌物主要是上部松散覆盖物，是由内至外、由下至上发展；范刚［10］通过模型试验研究了含软弱夹层层状岩质边坡地震响应并提出了稳定性判别方法；蒋薇等［11］基于极限平衡理论提出了确定地震荷载作用下加筋土边坡滑裂面的水平条分法；祝珣［12］研究了某黄土边坡坍塌的原因和治理方案；张翾等［13］通过现场测试和有限元软件计算分析了某隧道洞口段边坡的坍塌原因及过程；吴峰等［14］研究了岩溶边坡的滑塌过程并提出了稳定性分析方法；张建明［15］等通过鲁甸8.0 级地震调查了公路边坡的破坏类型，认为边坡坍塌与土的饱和程度有关。

目前针对地震作用下边坡破坏的原因和防治措施已经有了较为丰富的研究，但对于特殊类型的边坡坍塌破坏过程研究仍然较为匮乏，难以发现、描述和控制边坡地震破坏过程，对交通安全有极大的威胁。

本文通过模型试验观测地震作用下基覆型边坡坍塌破坏的现象，并监测边坡的加速度和位移；运用Hilbert-Huang Transform （HHT）方法，进行边坡坍塌全过程的地震动响应特征分析，相关结论对边坡工程的发展有一定的参考价值。

1 振动台模型试验概况

由于岩土体长期受到自然力的影响，具有较大的离散性和颗粒性，理论计算和计算机模拟往往难以得到岩土动力特性的精确解答，而使用物理模型试验能得到与实际情况更为接近的结果［16］。下文以川藏铁路沿线位于理塘—德巫断裂带附近的典型边坡为原型，设计模型与其相似比为1∶10，通过振动台试验模拟边坡坍塌的过程。值得注意的是，由于地下水会导致边坡坍塌变形难以控制，为避免其影响，本试验不设置地下水。

1.1 模型制作

由于坍塌是边坡结构出现的局域性破坏，在坡度较高且边坡土体较为松弛时容易出现，这是由于应力波从坚硬岩土体传入软弱土层时在界面处将会存在有较大的拉应力，因此本试验设置堆积土作为滑体，中间设置软弱夹层，下部设置硬岩层，根据相似理论对试验模型进行设计［17］，主要过程如下。

选取试验相关的物理量，根据π定理［18］，物理量之间需满足特征方程

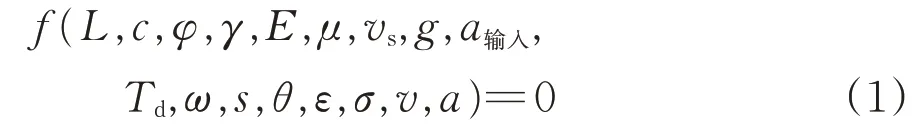
式中：L为几何尺寸；c为黏聚力；φ为内摩擦角；γ为重度；E为动弹性模量；μ为动泊松比；υs为剪切波速；g为重力加速度；a输入为输入加速度；Td为持续时间；ω为振动频率；s为线位移；θ为角位移；ε为应变；σ为应力；v为速度；a为响应加速度。

将上述物理量无量纲化后，能够得出相似准则的表达式，并得出相似关系。

设控制量为几何尺寸、重度和重力加速度，上述控制量的原型与模型相似比分别取10∶1，1∶1和1∶1，根据相似关系计算相应参数的原型与模型相似比，黏聚力为10∶1，内摩擦角为1∶1，动弹性模量为10∶1，动泊松比为1∶1，剪切波速为3.16∶1，输入加速度为1∶1，持续时间为3.16∶1，振动频率为0.316∶1，线位移为10∶1，角位移为1∶1，应变为1∶1，应力为10∶1，速度为3.162∶1，响应加速度为1∶1。

试验选用水、河砂、石膏、黏土为原材料制作模型边坡，包括滑体（堆积体）、软弱夹层和滑床（基岩）结构，其中滑体为散粒土，滑床为以石英砂岩夹板岩为主的硬岩，分别进行分层填筑夯实。模型整体高度为1.5 m，坡高1.25 m，坡度约为50°，模型底部长2.21 m，宽2 m；上顶面长0.25 m，宽2 m。经室内试验得出堆积层的基本性能参数，其天然含水率约为10%，密度ρ为1.91 g·cm-3，黏聚力c为5.50 kPa，内摩擦角φ为37.90°。试验使用的振动台台面长度和宽度均为3 m，使用的模型箱两侧装配有12 mm 厚的有机玻璃以实现可视化，并在模型边界上涂抹润滑剂以减少摩擦，并在模型与钢板接合处安置泡沫板以减少边界效应。

1.2 模型监测点设置

为监测边坡坍塌过程，选用加速度传感器及位移传感器对坡面进行监测，模型监测点布置如图1所示。图中位移传感器测点为D1—D3，加速度传感器测点为A1—A3。

图1 模型监测点布置图

1.3 地震波

试验选取归一化后的实测汶川卧龙地震波、Kobe 地震波以及El Centro 地震波作为输入波，每次加载地震波前均施加白噪声，通过依次逐级加载0.1g，0.2g，…，1.0g峰值加速度的汶川卧龙地震波、Kobe 地震波以及El Centro 地震波，从而模拟不同烈度地震荷载，研究边坡坍塌过程。地震波加载方向为坡面至临空面水平向，地震波波形如图2所示。

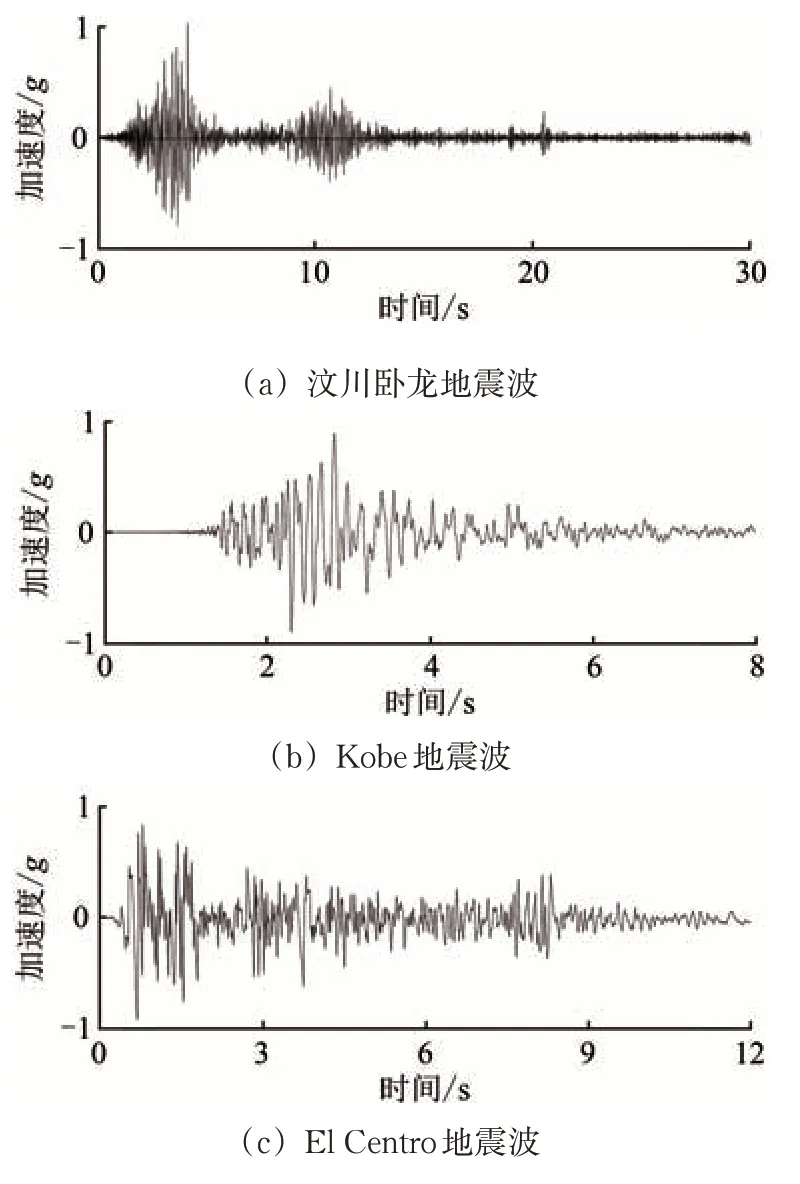
图2 地震波波形

2 HHT分析方法

HHT 是一种处理振动信号的典型方法［19］，能较好地反映地震动响应的频谱特性，已有学者将其运用到结构损伤判别之中［20］。HHT 分析方法主要分为2 个步骤，即经验模态分解（Empirical Mode Decomposition，EMD）和Hilbert 谱分析（Hilbert Spectrum Analysis，HSA）。主要过程如下。

（1）基于局部极值点作出监测信号x(t)的上包络线Xmax(t)和下包络线Xmin(t)，在原序列x(t)中减去上下包络线的平均值m1(t)，得到新序列h1(t)，并判断其是否满足固有模态函数（Intrinsic Mode Function，IMF）的要求，如满足该要求，则令该序列为第1 个IMF 分量，否则将h1(t)替换原序列并重复上述过程，直到IMF分量出现。

（2）将IMF 分量从原序列中剔除，将剩余序列作为新的原序列继续求下1个IMF分量，直至剩余序列Rn(t)变为单调函数或小于某阈值时结束。

（3）将IMF分量h(t)与1/(πt)卷积，即

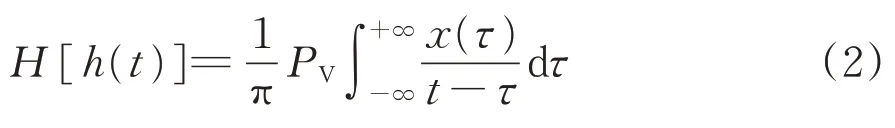
式中：PV为柯西主值；x(τ)为各阶IMF 分量；τ为频率。

在振幅-时间平面上，原信号可表示为

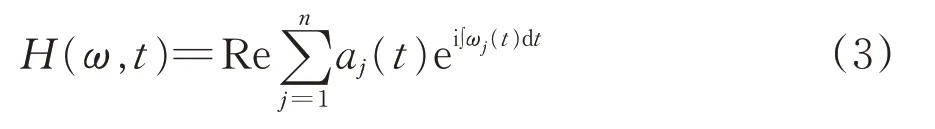
式中：n为IMF 分量的数量；aj(t)和ω(t)分别为IMF分量的瞬时振幅和瞬时频率。

HHT 的优势在于减小了傅里叶变换的拟合误差，有效避免了海森堡不确定性原理中时间与频率之间的对应性问题［21］，适用于突变信号，且能同时表征结构振动过程中的时域及频域响应。因此，使用HHT 方法研究边坡地震动响应可以较为准确地反映土体受力状态的变化情况。

3 地震作用下基覆型边坡坍塌特性

下文根据试验现象及传感器响应结果，进行边坡坍塌特性分析。

3.1 试验现象

在输入峰值加速度（Peak Ground Acceleration，PGA）为0.3g的El Centro 地震波时，边坡出现部分碎屑流，总体上保持稳定，无肉眼可见的裂缝，如图3所示。

图3 PGA为0.3g的El Centro地震波作用下边坡变形

在输入PGA 为0.6g的El Centro地震波时，边坡发生剧烈碎屑流，坡面上部出现裂缝，滑体部分位置坍塌，坍塌位置主要在坡面下部，可见剧烈碎屑流，同时有坡面凸起发生，同时软弱夹层和硬岩间出现滑坡现象，如图4所示。

图4 边坡坍塌过程

3.2 边坡坍塌过程

由于岩土体结构动力变形形式极为复杂，在地震动荷载作用下使岩土体发生瞬时位移后，岩体能够依靠自身特性抵消应力波［22］，根据试验现象、位移响应及加速度HHT 谱，可将边坡在地震作用下的坍塌阶段划分为边坡稳定振动阶段、裂缝扩张阶段和坍塌破坏阶段。

3.2.1 边坡稳定振动阶段

图5 给出了输入PGA 为0.1g的El Centro 地震波时边坡各测点的位移。由图5 可见：位移变化范围始终保持在0.1 mm 左右，且无永久位移，说明该点处地震动响应较小，下部硬岩及上部堆积体已经耗散了大部分能量，输入汶川卧龙地震波和Kobe 地震波时边坡各测点的位移相似，在此不再赘述。

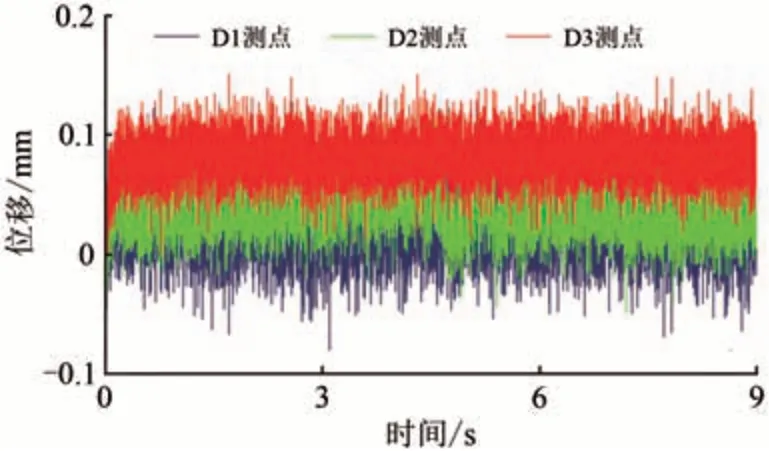
图5 输入PGA为0.1g的El Centro地震波时坡面位移时程

图6 给出了输入PGA 为0.1g的不同地震波时坡面A3测点加速度的HHT 谱。由图6可知：汶川卧龙地震波作用下该测点在0～20 s 时的加速度HHT 谱幅值较高，Kobe 地震波作用下该测点在2～4 s 时的加速度HHT 谱幅值较高，El Centro 地震波作用下该测点在2～4 和6～8 s 时的加速度HHT 谱幅值较高；不同地震波作用下该测点加速度的HHT 谱在时域分布较为集中，在频域上卓越频段均位于0～25 Hz 之间；加速度HHT 谱的幅值大小顺序为汶川卧龙地震波＞Kobe 地震波＞El Centro 地震波；在输入El Centro 地震波时加速度的HHT 谱会出现多个幅值明显的时域带，这应当是El Centro 地震波卓越频率与边坡自振频率相近的原因。上述现象说明：不同类型地震波作用下边坡各位置的加速度HHT 谱响应有明显的差异，根据坡面测点位移和加速度HHT 谱可知，边坡此时还处于稳定状态。

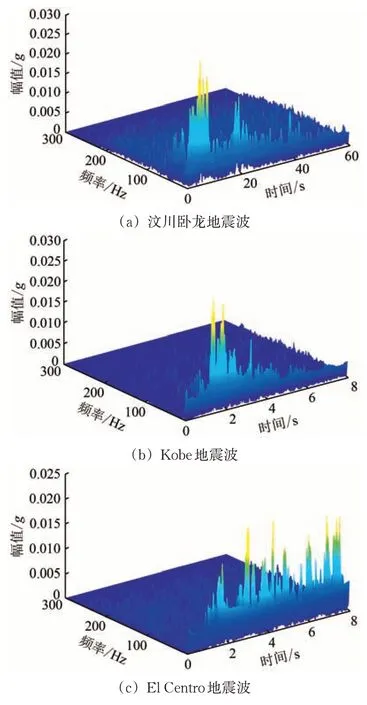
图6 输入PGA为0.1g的地震波时A3测点加速度HHT谱

综上可知，自然边坡在低烈度地震作用下还保有一定的抵抗能力，原因是岩土体内部的黏聚力、土-水间分子作用力等阻力可以抵消地震动荷载，由于该阻力主要由岩土体的介质特性决定，因此不同岩土体之间存在一定的差距，在此时期岩土体出现微弱位移，卓越频率较为集中，主要为低频振动。

3.2.2 边坡裂缝扩张阶段

在输入PGA为0.3g的汶川卧龙地震波及Kobe地震波时，D1—D3 测点位移变化较小，但在输入PGA 为0.3g的El Centro 地震波时，D1—D3 测点出现较为明显的突变位移，发生永久位移时间约为0.4 s″，约为0.1 mm，如图7 所示。此时A3 测点的加速度HHT 谱如图8 所示。由图8 可见：该测点在2～4 和6～8 s 的加速度HHT 谱幅值较高，且较图6（c）有明显增长，卓越频段仍然处于0～25 Hz 范围内，但位于50～75 Hz 的HHT 谱幅值明显提升，这应当是由滑体中的散粒土导致的，此时坡面虽然出现一定的碎屑流及微弱裂缝，但边坡仍能保持主体稳定，这与“累积效应”描述相符。该现象反映了边坡坡面防护的重要性，以减少碎屑流为目标进行坡面防护可有效提升中低地震烈度地区的抗震减灾能力。

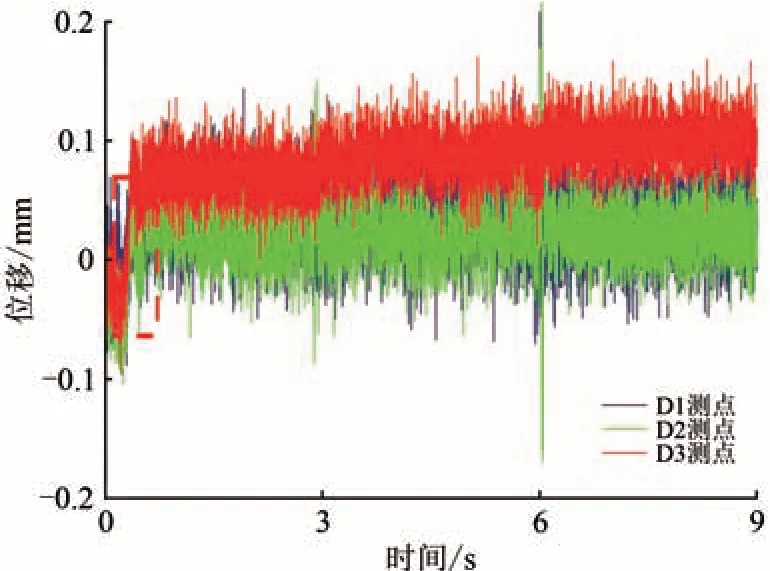
图7 输入PGA为0.3g的El Centro地震波时位移时程

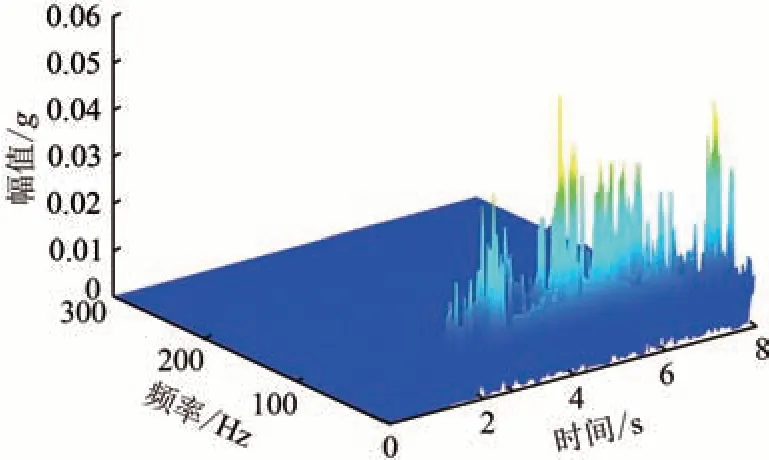
图8 输入PGA 为0.3g 的El Centro地震波时A3测点加速度HHT谱

输入PGA 为0.5g的3 种地震波都导致边坡坡面发生较大永久位移，图9 给出了坡底的D3 测点位移。由图9 可见：汶川卧龙地震波作用下坡底永久位移最大，约为0.5 mm，El Centro 地震波次之，Kobe 地震波最小，这应当是由于汶川卧龙地震波持时最长的原因。

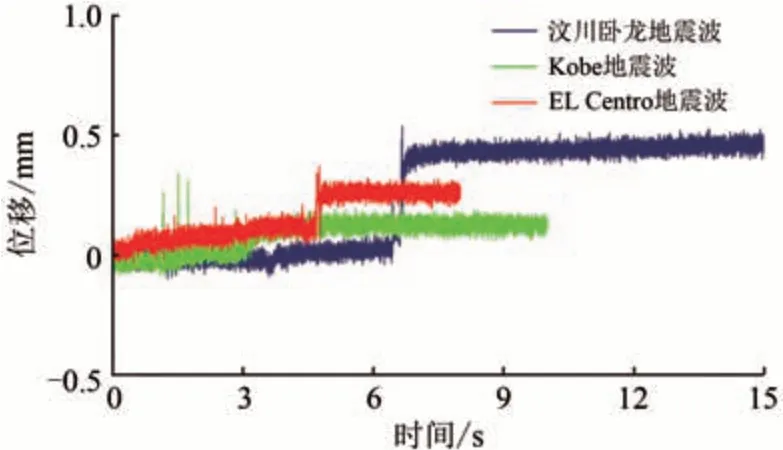
图9 输入PGA为0.5g的地震波时D3测点位移时程

图10给出了不同地震波作用下A3测点的加速度HHT 谱。由图10 可见：在输入PGA 为0.5g的地震波作用下该测点的加速度HHT 谱幅值较输入PGA 为0.1g的地震波时有较大提升；该测点在El Centro 地震波作用下加速度HHT 谱仍存在多个幅值明显的时域带；位于50～75 Hz 频率范围内加速度HHT谱幅值有明显增大。

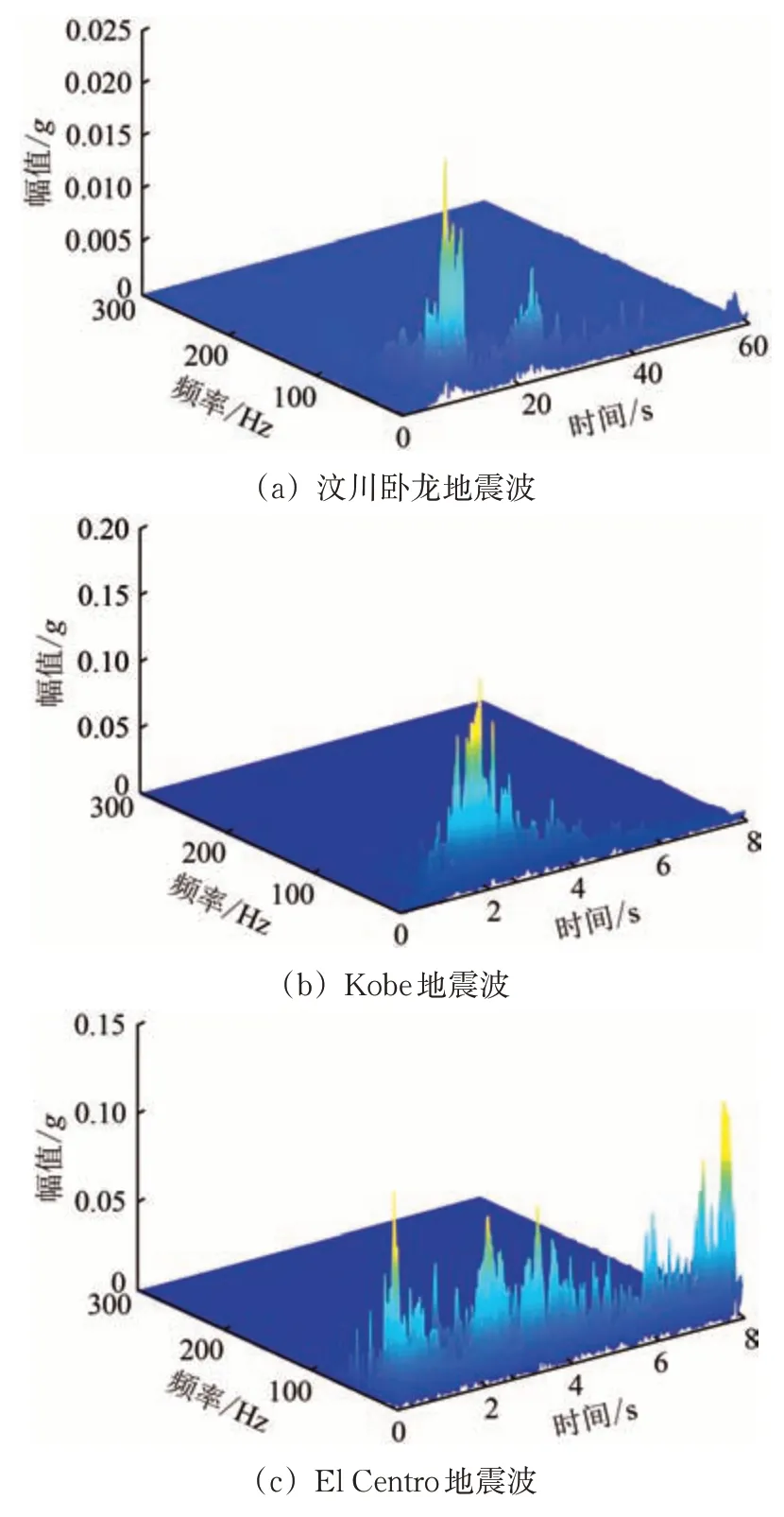
图10 输入PGA为0.5g的地震波时A3测点加速度HHT谱

根据位移响应的变化大小可知此时边坡坡面裂缝进一步扩大，土体内部节理面扩大，部分土体发生位移后不能复原，根据加速度HHT 谱可知由于地震波在增强后在节理面、坡面等位置由于折射反射和叠加而造成破坏效应增强，因此可以认为结构进入破坏前的临界状态。

综上可知，边坡岩土体在承受PGA 较大的地震动荷载后其本身的抗震能力已经难以耗尽地震波能量，原因是岩土体之间的孔隙逐渐扩大，导致其力学强度急剧降低，土体张拉应力超过极限强度，出现节理面并继续发展。值得注意的是，在进行逐级加载时由于“累积效应”，岩土体在地震力作用下可能在一瞬间会出现剪切失稳，但并不破坏，直到剪切面中的锁固段被突破或越过某些凸起体后才导致最终破坏。

3.2.3 边坡坍塌破坏阶段

图11—图13 给出了在输入PGA 为0.6g地震波时D1—D3 测点的位移时程。由图11—图13 可见：3 个测点的位移变化曲线较为相似，且位移大小顺序为D3 测点＞D2 测点＞D1 测点，汶川卧龙地震波作用下＞Kobe 地震波作用下＞El Centro 地震波作用下；坡面3个测点的位移时程表明坡面发生了剧烈变形，D1—D3 测点位移均超过10 mm，但变化趋势相近，说明地震波对边坡坡面造成的位移变化较为一致，滑体还保持相对稳定，坍塌是局部破坏现象。

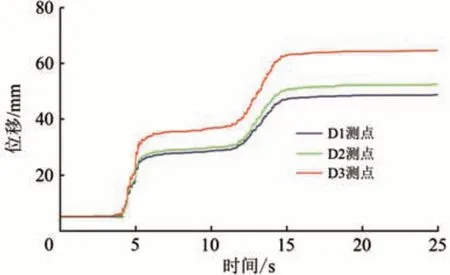
图11 输入PGA为0.6g的汶川卧龙地震波时坡面位移时程

图12 输入PGA为0.6g的Kobe地震波时坡面位移时程

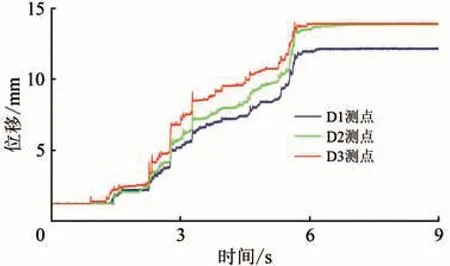
图13 输入PGA为0.6g的El Centro地震波时坡面位移时程

图14 给出了A1—A3 测点的加速度HHT 谱。由图14可见：在时域分布上，加速度HHT 谱幅值均值上A1测点＞A2测点，这与坍塌和变形主要位置（坡面下部）的距离相近；在大小关系上，A1测点的加速度HHT 谱幅值最大，且与其他2 个测点相比加速度HHT 幅值更大，说明坍塌区域出现较大的应力波动，原因是土体结构出现剧烈变形，加速度HHT 谱幅值变化加剧，该处裂缝面贯通，土体发生坍塌。

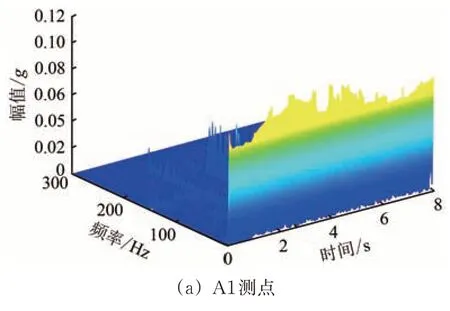
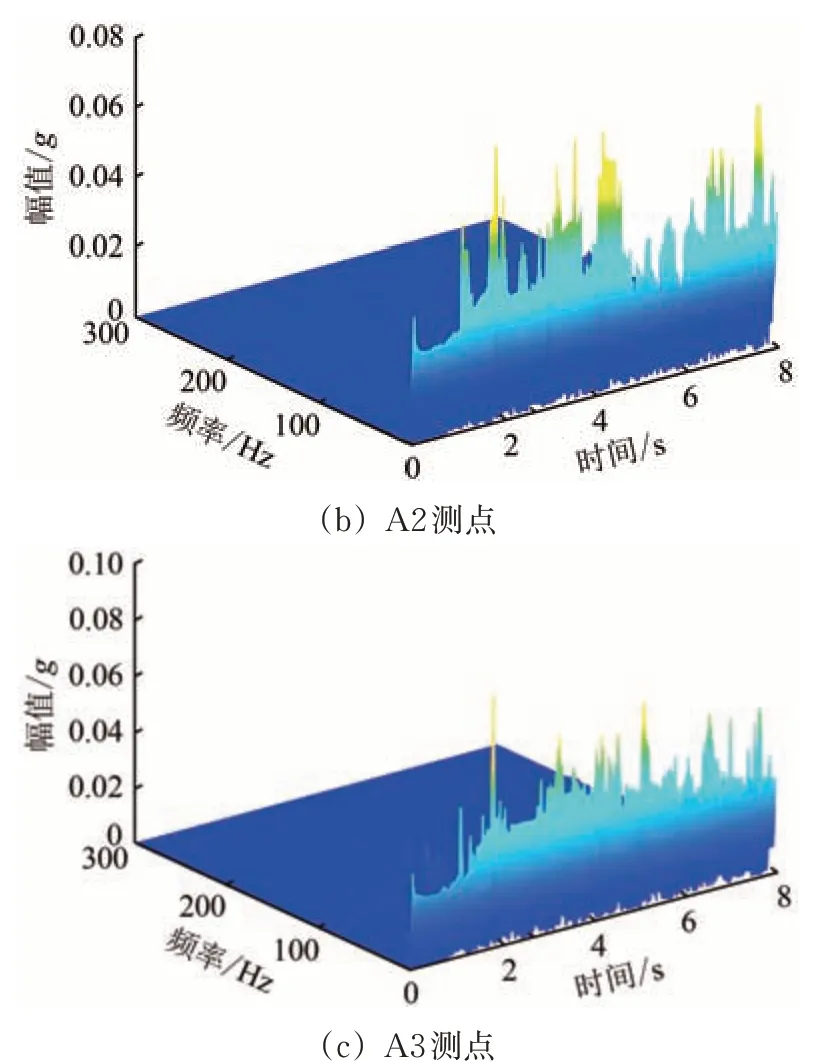
图14 输入PGA为0.6g的El Centro地震波时HHT谱

综上可知，边坡坍塌前岩土体内部松弛，加速度HHT 谱幅值波动明显，裂隙面不断扩大，部分土体位移后不能复原，边坡抵抗外力能力降低，伴随坡面碎屑流现象，在承受较大地震荷载后，土内锁固面被突破发生严重变形，最终导致坡面坍塌，同时还可能发生错落，此后将演变为崩塌或滑坡，HHT方法对于边坡坍塌特性能够进行有效分析。