超高性能混凝土增强普通混凝土复合梁受弯承载力

2021-10-19蔺鹏臻杨子江

中国铁道科学 2021年5期

雒敏，蔺鹏臻，杨子江

（兰州交通大学土木工程学院，甘肃兰州730070）

超高性能混凝土（Ultra-High Performance Concrete，UHPC）是一种掺入不同活性粉末及纤维材料的水泥基复合材料。UHPC 抗压强度高、韧性及耐久性好，具有拉伸应变硬化等优异特性，特别适用于超大跨度、超高层结构建设以及既有旧结构加固等领域。

国内外学者针对UHPC 试块、UHPC 梁和UHPC 板等UHPC 结构做了大量的力学性能研究。SHAMSAD 等［1］分析了水养护、自然养护及钢纤维含量对UHPC 抗压强度和弹性模量的影响，发现在一定程度上纤维含量的增加可以提高UHPC抗压强度和弹性模量。RUI 等［2］对不同掺和料的UHPC 进行力学、经济和环境等方面的综合评判，提出了综合效果最好的UHPC 掺和料配合比。朋改非等［3］通过高温后混凝土的残余断裂能、残余抗压强度和残余劈裂抗拉强度等特性对比分析了UHPC 和活性粉末混凝土的优劣，结果表明，高温后UHPC 的残余抗压强度较好，适用于受压结构，而活性粉末混凝土的残余断裂能和残余劈裂抗拉强度较好，适用于受弯结构。郭晓宇等［4］基于UHPC 单轴受压试验的抗压强度、峰值应变和弹性模量等试验数据特征，提出修正系数法拟合UHPC 本构关系，该方法拟合结果具有较高的精度。欧阳雪等［5］采用试验分析了不同水胶比及粗骨料对UHPC 受压性能的影响，并结合试验结果提出了考虑粗骨料影响的UHPC 弹性模量半经验计算公式。

UHPC 梁是常用的UHPC 结构之一，为进一步促进UHPC 结构的应用及发展，对UHPC 梁进行受弯性能研究是非常必要的。杨剑等［6］通过3点弯曲梁试验分析了UHPC 梁受弯力学性能，并结合模型试验结果提出了UHPC 梁受弯承载力理论计算方法。马熙伦等［7］通过试验分析了5 根钢筋UHPC 梁的受弯破坏形态、荷载-挠度曲线、截面应变等，并结合试验结果提出了不同纤维掺量下的钢筋UHPC 梁受弯承载力理论计算方法。可知，既有研究大多将UHPC 视为整体材料，通过试验及理论计算分析UHPC 力学性能［8-9］，但UHPC主要由常规混凝土基材和钢纤维两部分组成，其性质更加类似于钢筋混凝土结构。因此，有必要基于细观力学理论将UHPC 中钢纤维作为主要受拉材料来分析UHPC 增强普通混凝土复合梁受弯性能，以期为UHPC的推广应用提供理论补充。

本文以UHPC 增强普通混凝土复合梁（简称复合梁）为研究对象，进行受弯性能试验，分析复合梁受弯破坏形式及力学特性；基于细观力学理论提出复合梁受弯承载力计算式，并结合试验结果进行验证。

1 复合梁受弯性能试验

复合梁长度为400 mm，截面宽100 mm，高100 mm。复合梁包括UHPC 和普通混凝土2 个部分。普通混凝土采用常规C40混凝土材料。UHPC材料为：水泥采用甘肃祁连山牌P·O 52.5 级水泥；砂为剔除颗粒直径大于1.18 mm 的标准砂；减水剂为减水率大于30%的聚羧酸高效减水剂；纳米二氧化硅采用20 nm 的超细型；硅灰采用上海埃肯公司生产的微硅粉；钢纤维采用赣州大业公司生产的长度8 mm 的钢纤维。纳米二氧化硅和钢纤维的材料性能指标分别见表1和表2。

表1 纳米二氧化硅性能指标

表2 钢纤维性能指标

采用钢纤维体积掺量为2.0%时对应抗压强度fcu为138.41 MPa 的UHPC，配合比为水泥∶砂∶硅灰∶水∶水胶比∶减水剂∶纳米二氧化硅＝1∶1.2∶0.2∶0.244∶0.2∶0.02∶0.02。

复合梁采用湿浇方式黏结，即先浇筑底层UHPC，振捣密实并抹平其上表面后立即浇筑上层普通混凝土再振捣密实。UHPC 参照标准GB/T 31387-2015《活性粉末混凝土》［10］制作。试件成型24 h后拆模，标准养护28 d，将试件擦拭干净后进行试验。

按UHPC 层不同高度占比设计了5组试验，每组3 片复合梁共计15 片。复合梁尺寸为400 mm×100 mm×100 mm，从1 组到5 组复合梁截面UHPC高度分别为0，15，25，50和100 mm。

加载试验如图1 所示，跨中截面沿高度方向布置电阻应变片测量应变，跨中及1/4 跨处布置百分表测量复合梁挠度。加载方式为单调逐级加载，每级加载的荷载增量为2 kN，直至复合梁破坏［11-13］。

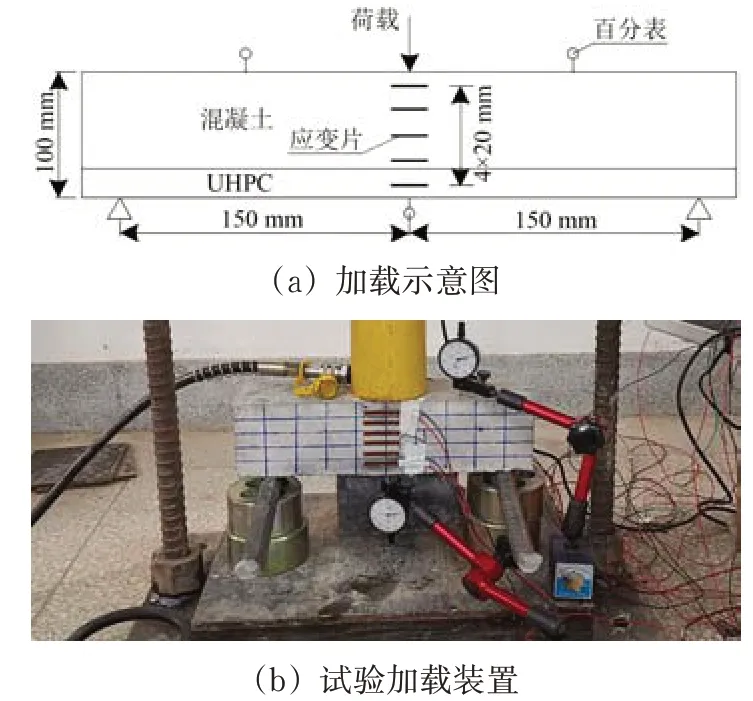
图1 复合梁加载试验

2 试验结果及分析

2.1 复合梁跨中截面应变

图2 为不同荷载作用下的复合梁跨中截面应变沿截面高度分布曲线，以拉为正。

由图2 可知：复合梁截面应变与截面高度呈较好的线性关系，满足平截面假定；UHPC 高度越大，复合梁的变形能力及临近破坏时的持荷能力越强；各荷载工况下中和轴基本在截面中心处，UHPC高度较大时中和轴有向上移动的趋势，如图3所示。

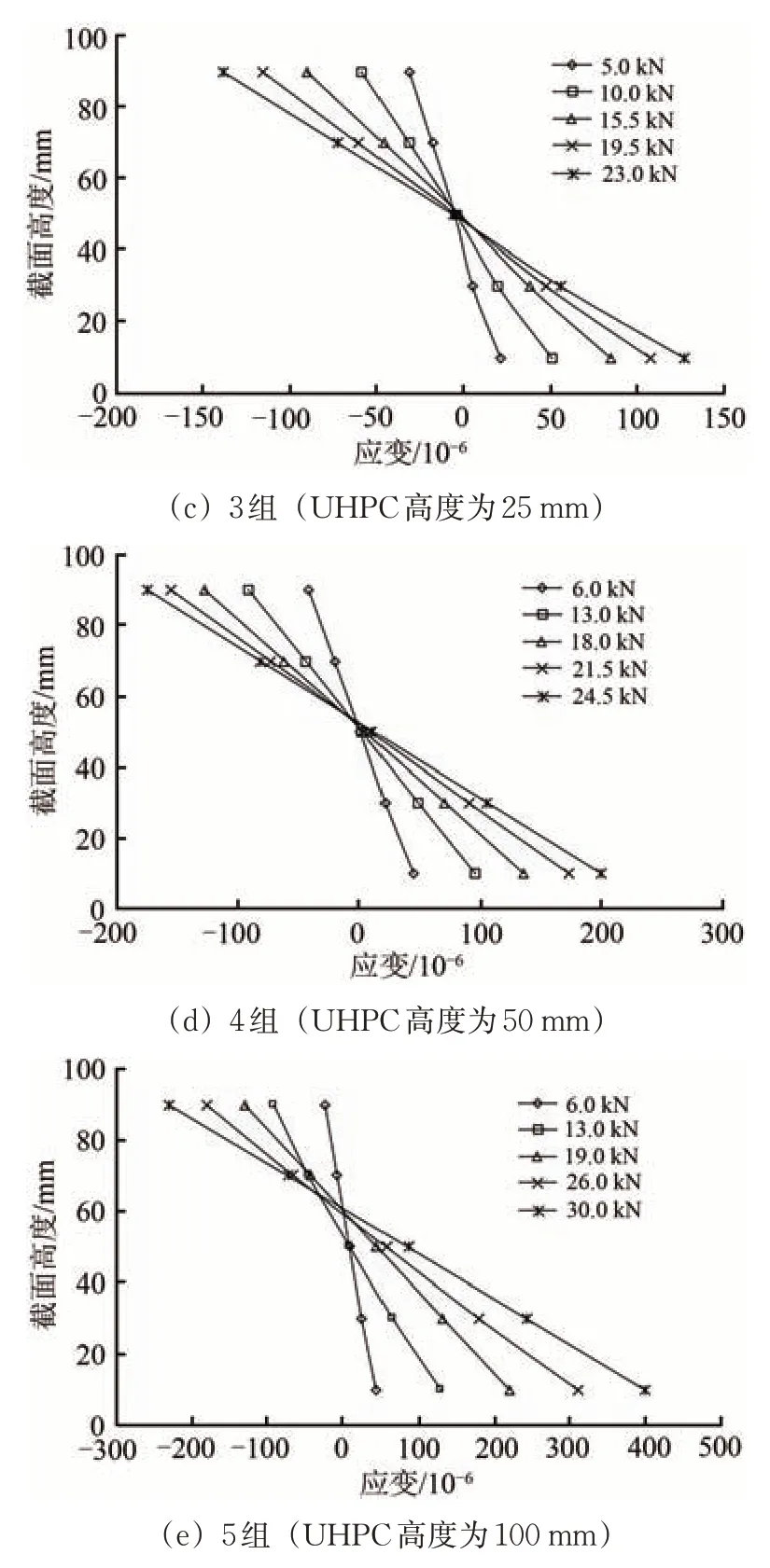
图2 不同荷载作用下跨中截面应变沿梁高分布

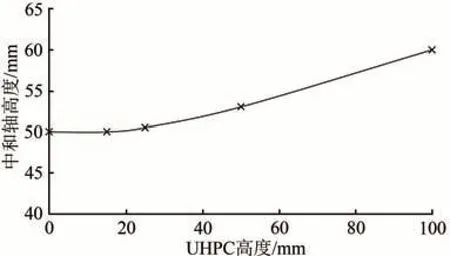
图3 中和轴高度与UHPC高度关系曲线

2.2 复合梁破坏形态

根据UHPC 高度的不同，复合梁破坏形态主要分为2种类型。

（1）无UHPC 或UHPC 高度较小时，复合梁受弯破坏形态与普通混凝土梁类似，极限荷载前，复合梁表面无可见裂缝；极限荷载后，竖向裂缝一旦出现便迅速贯通整个截面，复合梁一分为二，出现明显的脆性破坏，如图4（a）所示。

图4 复合梁破坏形态

（2）UHPC 高度较大时，复合梁破坏形态随UHPC 高度增加由脆性破坏逐渐转为塑性破坏。复合梁下表面先出现若干条细小微裂缝，随着荷载的增加，其中一条裂缝逐渐发展为贯通主裂缝，伴随着裂缝宽度的增大及裂缝向上发展过程常听到纤维被拔出、拉断的“啪啪”声。加载结束时复合梁断裂面仍被纤维紧密连接在一起，未见脆性断裂等现象，如图4（b）所示。该现象表明纤维具有较强的控裂增韧能力，使得复合梁在裂缝较多及宽度较大时仍具有一定的承载力及变形能力，避免了复合梁脆性破坏。复合梁承载力及变形能力随UHPC高度的增加而提高。

2.3 承载力与变形关系

图5 为不同UHPC 高度下复合梁的荷载-应变曲线及挠度曲线。因应变片量程限制及安全考虑，试验中未采集到复合梁破坏阶段应变，且在观察到裂缝较大时即卸下百分表。

由图5 可知：加载初期，荷载相同时1 组复合梁挠度小于5 组，但大于其他3 组。分析原因，主要有以下2 点。①1 组和5 组梁均为1 次浇筑成型，而其他组复合梁为分层浇筑且每层浇筑后均进行了振捣密实成型，复合梁开裂前1 组和5 组梁的刚度小于其他3 组，因此荷载相同时挠度大于其他3组。②1 组梁采用常规C40 混凝土材料，掺合料中包含有大量碎石等粗骨料，而5组整体UHPC梁中掺合料粒径均较小，其性质与水泥砂浆类似，因此，1 组梁开裂前的初始刚度大于5 组梁，其挠度小于5 组。此外，复合梁开裂后，1 组梁刚度快速降低并随即破坏，而5 组梁在钢纤维的作用下随着荷载的增大截面挠度继续增大。

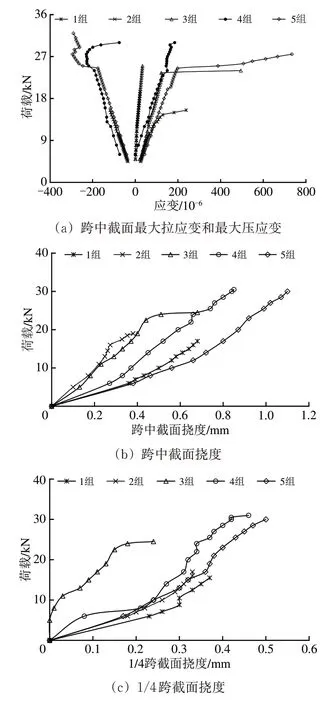
图5 复合梁荷载与变形关系曲线

UHPC 高度较大时，复合梁受弯破坏过程可分为：变形随承载力线性增大阶段（弹性阶段）、随着受拉区变形增大初始裂缝形成并向上发展阶段（裂缝阶段）和裂缝贯通整个截面阶段（破坏阶段）。

承载力是指结构或构件承受荷载或弯矩的能力，将结构或构件所能承受的最大荷载或最大弯矩称为极限承载力，它是结构设计时重要的评价指标之一。复合梁极限承载力见表3。

表3 复合梁极限承载力

由图5、表3 可知：荷载相同时，截面应变和截面挠度随着UHPC 高度的增大呈现总体增大的趋势；UHPC 高度越大，复合梁极限承载力越大，当UHPC 高度超过截面高度的一半后（4 组和5组），复合梁极限承载力增长幅度减缓，基本保持一致，但UHPC高度越大，复合梁的变形能力越强。

3 复合梁受弯承载力计算

3.1 基本假定

（1）不考虑混凝土拉应力，普通混凝土和UHPC 本构关系如图6 所示［14］。图中：σcp为普通混凝土抗压强度；εcp为极限弹性压应变；εcu为极限压应变；ft为UHPC 开裂抗拉强度；σUHPC为UHPC裂后抗拉强度；fcu为UHPC抗压强度；εtp为UHPC极限弹性拉应变；εtu为UHPC 极限拉应变；ε′cp为UHPC极限弹性压应变；ε′cu为UHPC极限压应变。

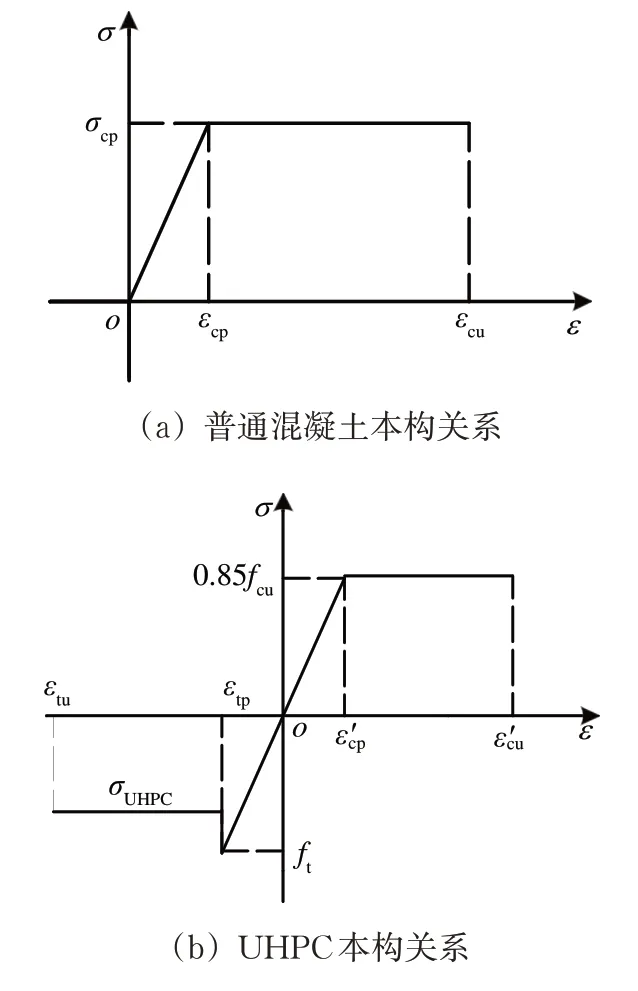
图6 普通混凝土和UHPC本构关系

（2）复合梁中UHPC 与普通混凝土间的界面黏结良好。

（3）纤维在UHPC中均匀分布。

3.2 UHPC抗拉强度

既有研究表明，在纤维作用下UHPC 具有高强、高韧等优良的力学特性，纤维的作用主要体现为纤维与UHPC 基体界面的黏结力。将UHPC 看作混凝土与纤维的混合物，基于细观力学理论计算UHPC 中单根纤维与UHPC 基体界面的黏结力。设单位面积内纤维的根数n［15］为

式中：ρ为纤维率，文中取2.0%；d为纤维直径。

则单根纤维与UHPC基体界面的黏结力F为

式中：τ为纤维与UHPC 基体界面的黏结应力；l为纤维长度。

因纤维在UHPC 中属乱向分布，假设UHPC中有m（m→∞）根纤维，任取1 根纤维进行受力分解，如图7 所示。图中：x，y和z轴分别为复合梁长度、宽度、高度方向；α为任一根纤维与xoy面的夹角；β为该纤维在xoy面上的投影与x轴的夹角。

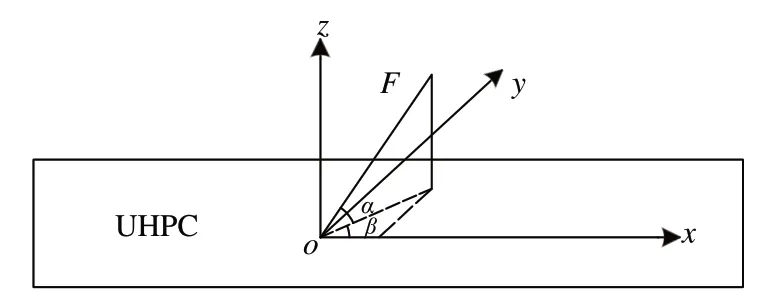
图7 纤维受力分解

第i根纤维与UHPC 基体界面的黏结力记为Fi，其值Fi=F。Fi在x方向的分力Fi，x为

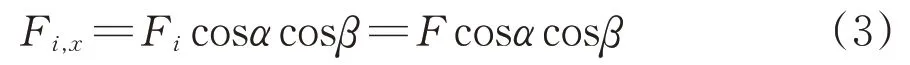
可得复合梁长度方向单根纤维和UHPC 基体界面的平均黏结力为

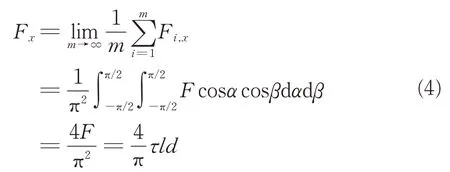
对于垂直于复合梁长度方向的任一截面，当纤维长度方向的中点恰好位于该截面上时，单根纤维能为该截面提供的最大拉力T为

而纤维未与截面相交时，纤维为该截面提供的拉力为0。采用平均拉力表征单根纤维沿复合梁长度方向能提供的有效拉力，即

则单位面积上纤维能提供的有效拉力（即UHPC裂后抗拉强度）为

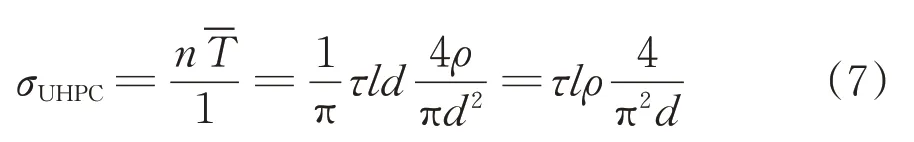
参考文献［16］，纤维与UHPC 基体界面黏结应力τ可取为故式（7）可写为

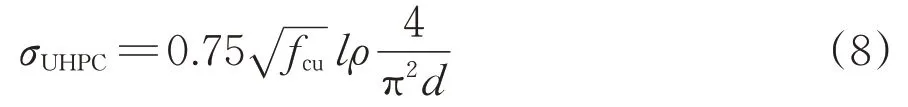
3.3 复合梁受弯承载力计算式

1）计算式推导

由试验结果可知复合梁受弯破坏过程主要分为3 个阶段：①弹性阶段，梁受力较小时，截面无裂缝产生，梁处于弹性阶段；②裂缝阶段，梁受力逐渐增大时，受拉区拉应力递增，微细裂缝逐渐形成，拉应力超过UHPC 极限拉应力后，裂缝以较快速度发展，受压区面积逐渐减小；③破坏阶段，随着梁所受荷载进一步增大，裂缝贯通整个截面，梁即破坏。

不考虑混凝土拉应力，且UHPC 中纤维与UHPC 基体界面的黏结力小于其抗压强度，复合梁受弯破坏各阶段截面应力应变分布如图8 所示。图中：h0和h1分别为复合梁梁高和中性轴高度；h2和h3为UHPC 高度和受拉区塑性高度；x为截面任一点高度；εc和σc为截面顶部的应变和应力；εt和σt为截面底部的应变和应力。

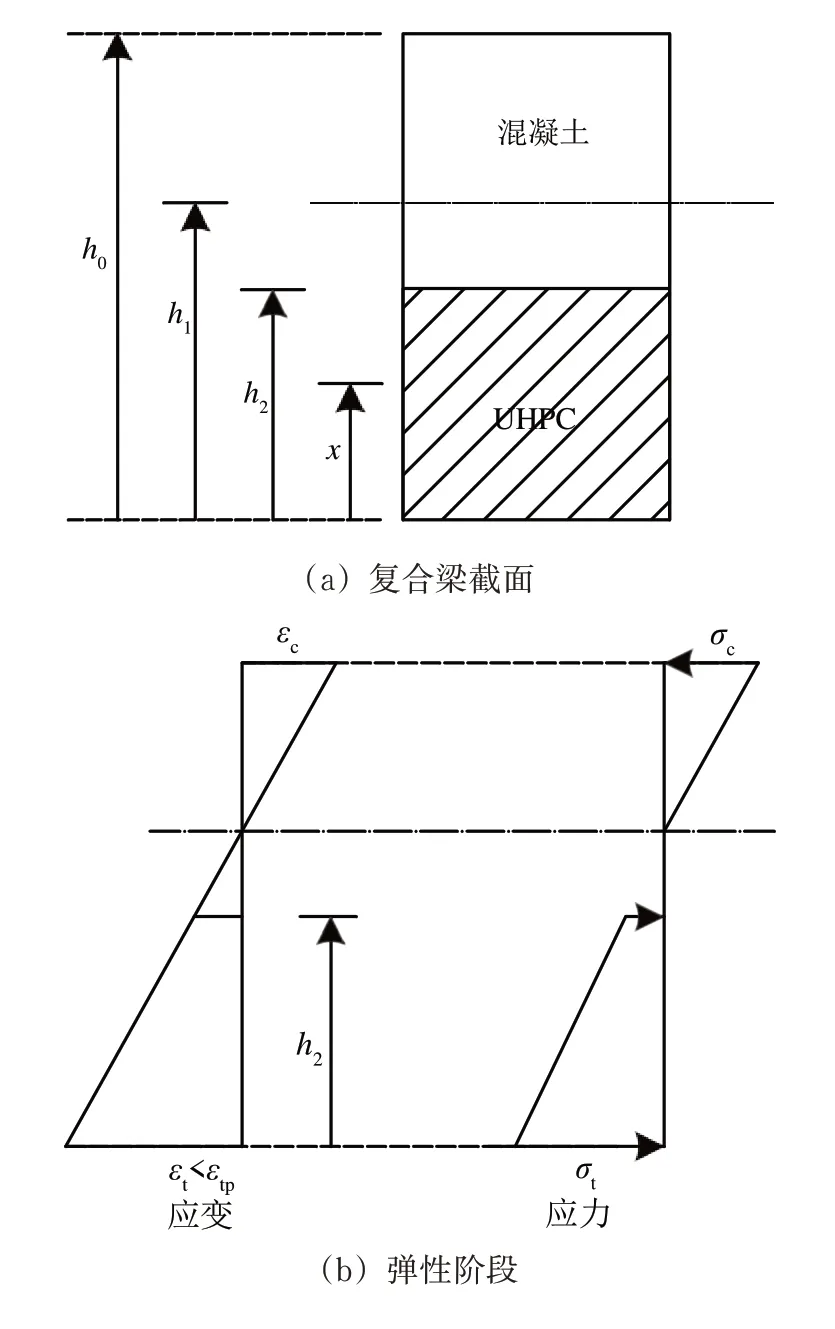
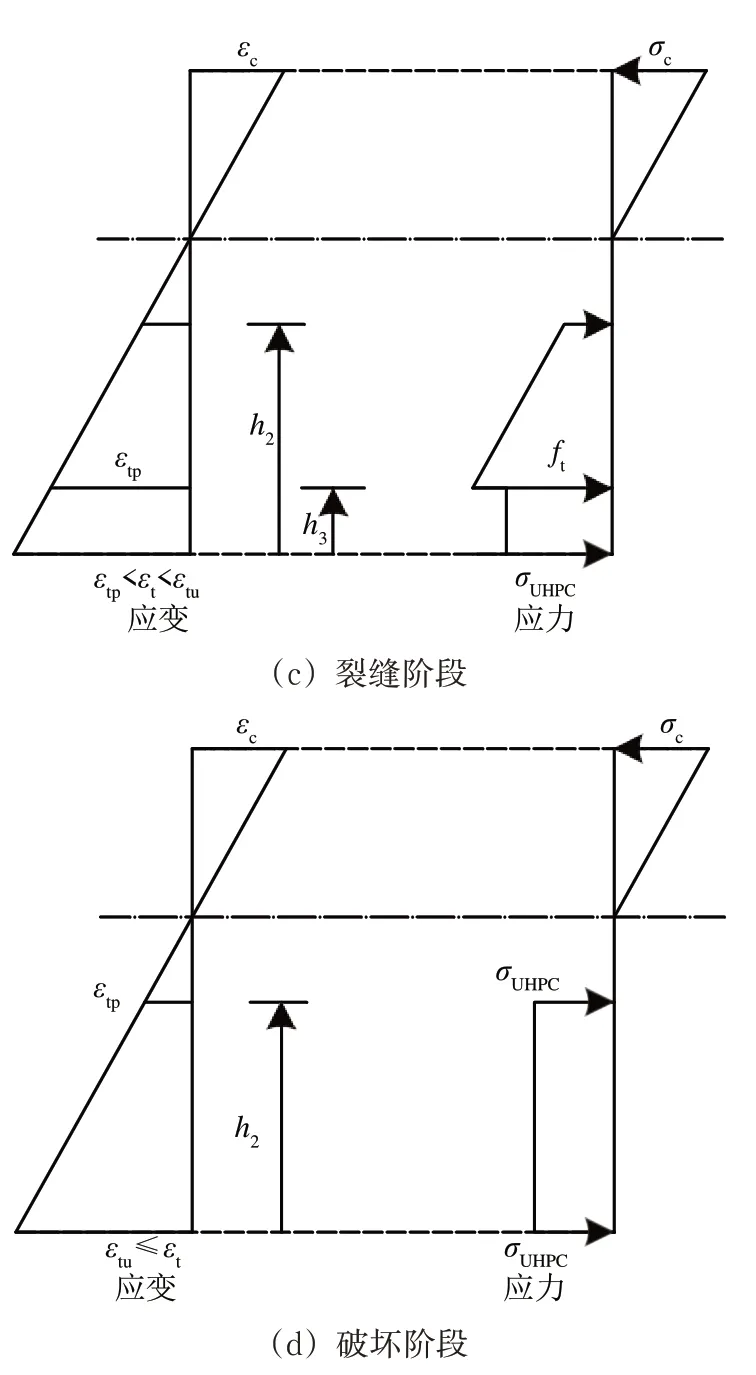
图8 复合梁截面及各阶段应力应变

各阶段截面应力分布如下。

（1）弹性阶段

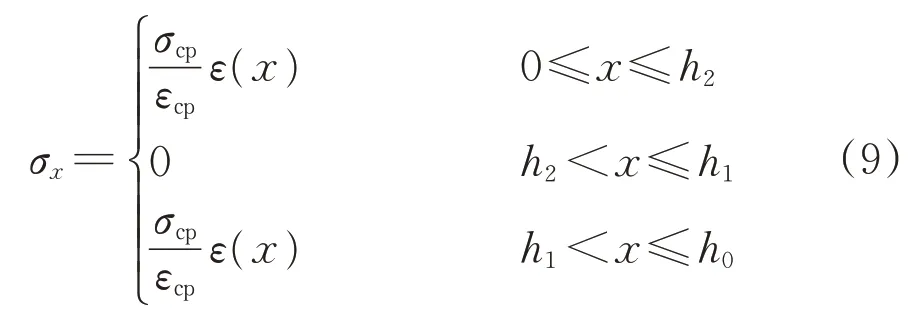
（2）裂缝阶段

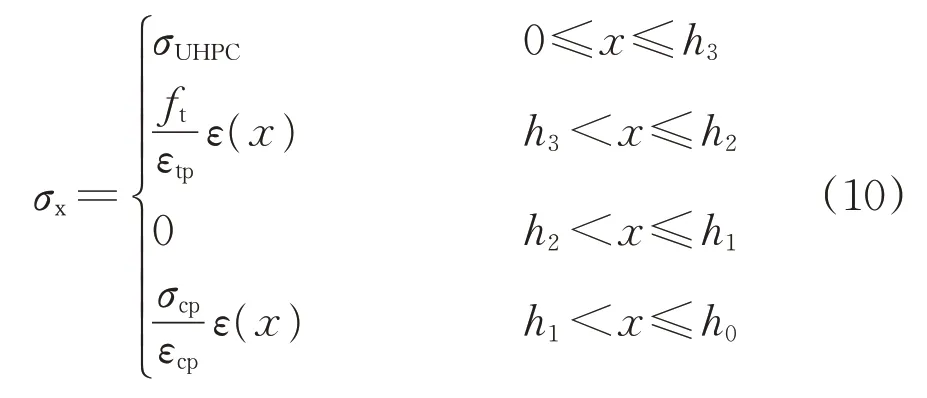
（3）破坏阶段

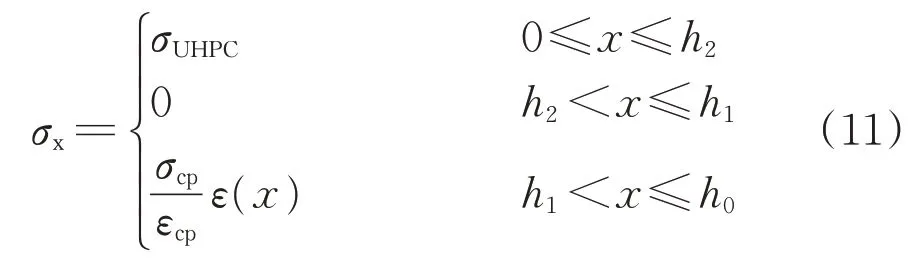
由平衡条件截面轴力为0，可得

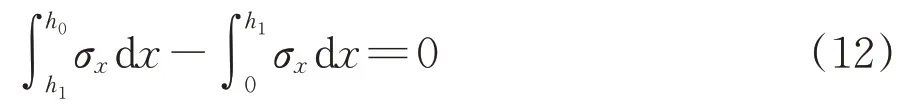
将式（9）—式（11）分别代入式（12），可得各阶段复合梁截面受压区高度。

则截面弯矩M计算式为

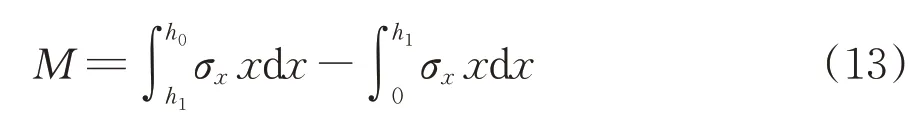
当受拉区UHPC 拉断时，可得复合梁截面受压区高度h1为

式中：Ec为普通混凝土弹性模量；EUHPC为UHPC弹性模量，其值由UHPC 立方体试件轴压试验测得，经测定钢纤维体积掺量为2.0%时的UHPC弹性模量为40 GPa。

则复合梁极限弯矩（即复合梁承载力）为

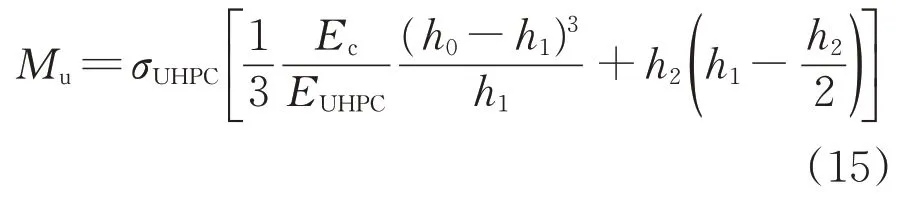
2）计算式验证

选取4种不同UHPC 高度的复合梁，将复合梁跨中弯矩-跨中截面最大压应变的计算值与试验值进行对比，如图9所示。

由图9 可知：本文基于细观力学理论提出的可考虑UHPC 高度变化的复合梁受弯承载力理论计算值与试验测试值基本一致，理论计算中不考虑受拉区混凝土拉应力。理论计算值与试验值均表明随着UHPC 高度的增大，极限状态时复合梁截面弯矩、截面变形呈增大的趋势，进一步说明了UHPC 具有较高的变形能力，即UHPC 高度越大，复合梁承载力和变形能力越大。

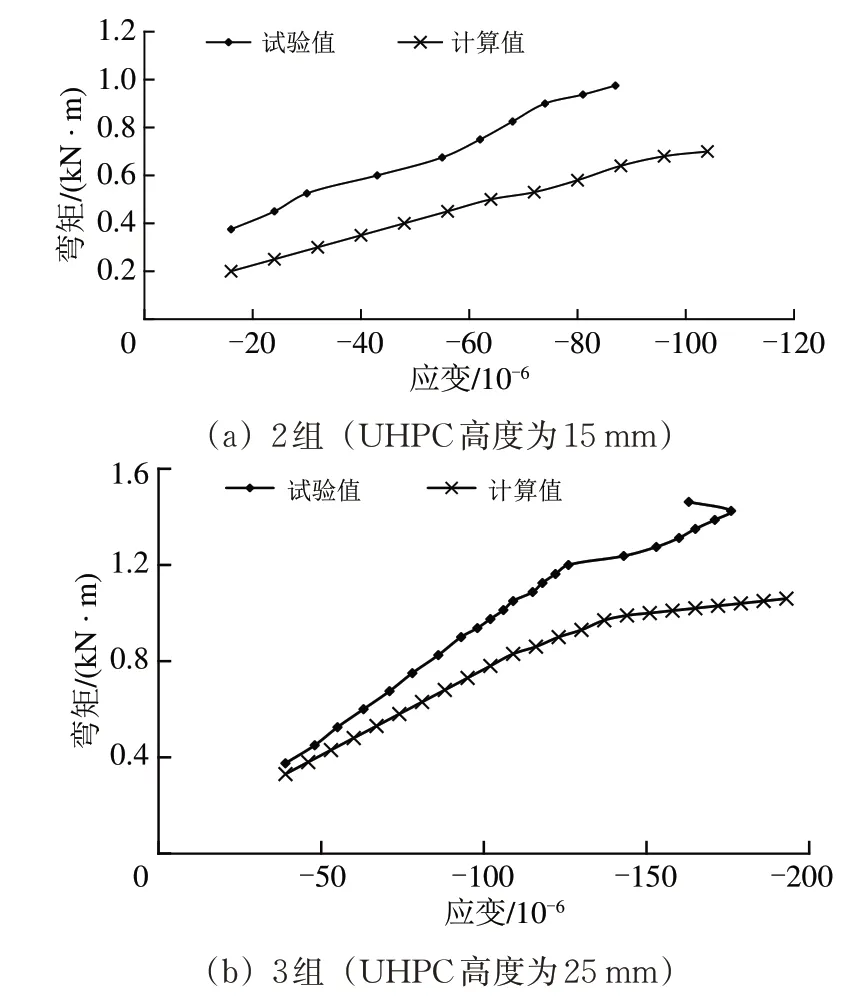
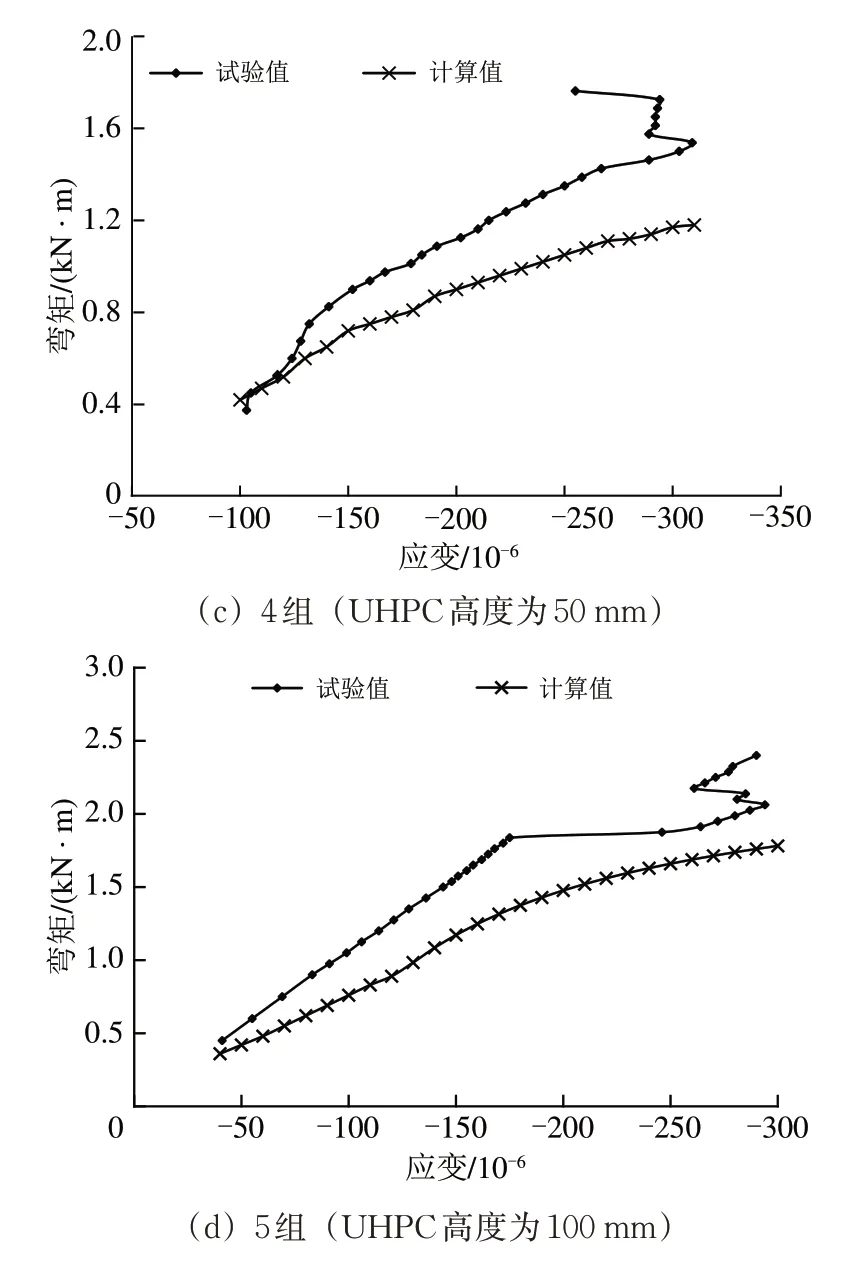
图9 计算与试验结果对比

3.4 影响因素

纤维率ρ、纤维长度l和UHPC 抗压强度fcu是影响复合梁承载力的重要因素。为评价其影响程度，提出纤维率、纤维长度和UHPC 抗压强度对复合梁承载力的增强指标—增大率μρ，μl和μfcu，计算公式如下。

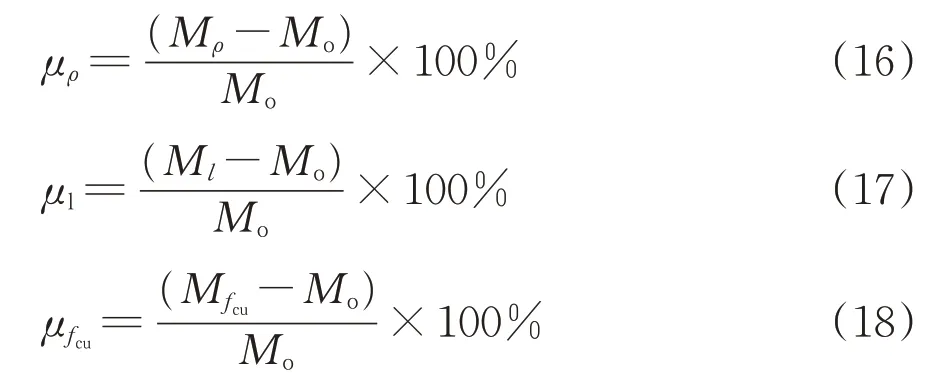
其中：Mρ，Ml和Mfcu为考虑不同纤维率ρ、纤维长度l和UHPC 抗压强度fcu后的复合梁承载力；Mo为不含纤维同尺寸梁承载力；纤维率ρ的取值为0.5%～3.0%，纤维长度l的取值为6～18 mm，UHPC抗压强度fcu的取值为100～160 MPa。

以3 组和4 组（UHPC 厚度分别为25 和50 mm）复合梁为例，根据式（16）—式（18）计算出不同UHPC 高度下复合梁承载力增大率的变化规律，如图10所示。

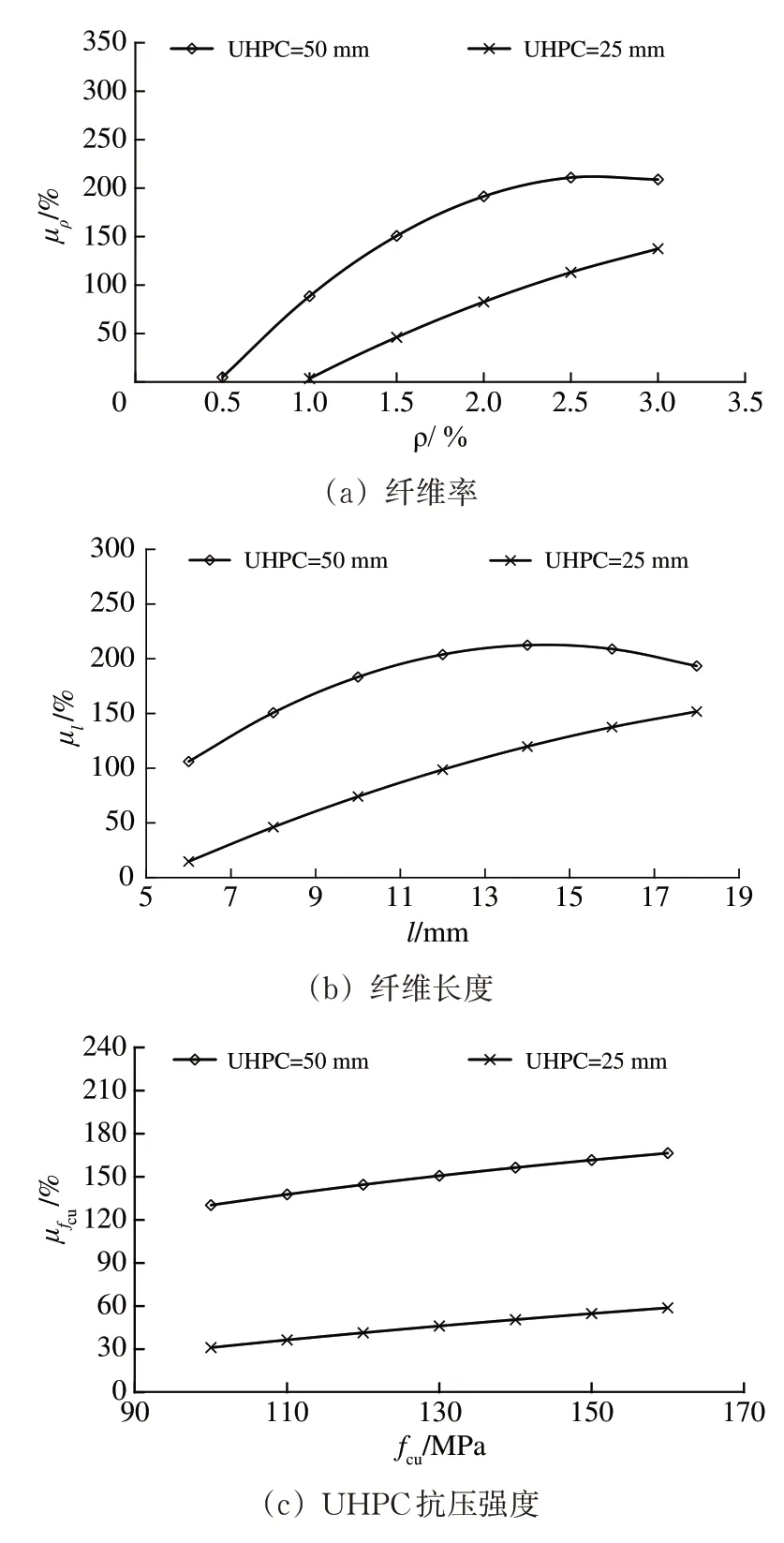
图10 不同参数对复合梁承载力的影响

由图10 可知：复合梁受弯承载力随纤维率ρ、纤维长度l、UHPC 抗压强度fcu的增大而增大；纤维特性对复合梁受弯承载力的影响较大，尤其纤维率的提高可大幅提升复合梁受弯承载力，但纤维率较高时纤维易发生团聚现象，建议纤维率取值在2.0%左右；UHPC 抗压强度的增大对复合梁受弯承载力的影响较小。因此，还可考虑适量增大纤维率的方法提升复合梁承载力，并且纤维率的提高有益于复合梁裂缝的控制。