带质心的K最近邻增强模糊最小最大神经网络的集成方法
2021-10-19赵建成余肖生
陈 鹏,赵建成,余肖生
(三峡大学 计算机与信息学院, 湖北 宜昌 443002)
解决稳定性-可塑性难题是ANN学习中的关键问题,尤其是当数据样本的数量随时间增加时,ANN模型必须以自主和增量的方式学习这些样本。为了解决稳定性-可塑性难题[1],Simpson[2]提出了2种混合的ANN模型(Fuzzy Min-Max(FMMN)网络),即模式分类的监督模型;模式聚类的无监督模型[3]。FMMN使用超盒模糊集在其网络结构中创建和存储知识,即作为隐藏节点,该网络已经得到了广泛的研究与应用,尤其是在分类任务上[2]。为了提升FMMN网络的性能,Mohammed等[4]提出了增强的模糊最小-最大神经网络(EFMMN),该算法在解决超盒的重叠测试和收缩测试时都更加有效。为了避免在获胜超盒附近产生过多的小超盒,从而降低FMMN的网络复杂度,Mohammed等[5]提出了K最近邻超盒展开规则的改进的模糊最小最大神经网络,实验表明通过该网络可以有效地降低网络的复杂度。Nandedkar等[6-7]提出了通用反射模糊最小-最大神经网络(GRFMN)。 GRFMM将FMM聚类和分类算法以及人体反射机制的概念组合到一个通用框架中,以解决重叠问题。刘金海等[8]提出了一种基于数据质心的模糊最小最大神经网络分类方法,该方法能够根据实际数据的质心特征自适应地调节超盒隶属度,从而来提高分类的精准率。
为了使FMMN实现半监督的能力,Ngan等[9]提出了模糊最小最大神经网络中的半监督聚类。Liu等[10]提出了一种基于模糊最小最大神经网络的半监督分类方法(SS-FMM)。在SS-FMM中,对模糊最小最大网络进行了修改,以处理标记和未标记的数据。
现有的FMMN及其变体,在训练网络以及进行最终预测时,都没有考虑之前训练的样本位于该超盒内的大体分布情况,仅计算样本点的隶属度的高低来选择扩展的超盒,这样不利于超盒更加准确的收缩以及最终精准的预测。同时,现有方法都过于依赖扩展系数的选择,如果选择糟糕的扩展系数,则会导致模型性能变差,另外对于每个数据集选择最佳的扩展系数也是非常耗费时间的事情。因此,提出了带质心的K最近邻增强模糊最小最大神经网络的集成方法(ensemble method ofk-nearest neighbor enhancement fuzzy minimax neural networks with centroid,简称为E-CFMM),该方法考虑了每个超盒数据集中的位置,即增加质心的同时,又集成了5个不同的扩展系数的弱分类器,并将5个弱分类器的预测结果作为随机森林的输入数据进行再训练。这样既可以不用考虑扩展系数的问题又能提高整体网络的预测性能。
1 K最近邻增强模糊最小最大神经网络
1.1 基本的模糊最小最大神经网络(FMMN)
FMMN的网络结构由3层组成,如图1所示。首先,Fa是输入层,其输入节点数等于输入要素数。其次,Fb是超盒层,每个Fb节点代表一个超级盒子模糊集。Fa和Fb节点之间的连接是最小和最大点,它们存储在2个矩阵V和W中,而隶属函数是Fb的传递函数[2]。第三,Fc是输出层,其节点数等于输出类数。

图1 FMMN网络结构
FMMN学习算法包括3个过程,即超盒扩展、超盒重叠测试和超盒压缩[11]。在FMMN是通过使用一组数据样本Ah来进行学习的,其中h=1…N,N是训练样本的总个数。根据训练样本,FMMN逐步创建许多超盒。每个超盒由单元超立方体(In)中n维空间中的一组最小和最大点表示。每个超盒模糊集定义为[5]:
Bj={Ah,Vj,Wj,f(Ah,Vj,Wj)},∀Ah∈In
(1)
式中:Bj是超框模糊集;Ah=(ah1,ah2,…,ahn)是输入数据;Vj=(vj1,vj2, …,vjn)和Wj=(wj1,wj2,…,wjn)分别是Bj的最小值和最大值。
当训练数据样本包含在超盒中时,则该数据样本具有该超盒的完全隶属度。超盒的大小由扩展系数控制,扩展系数的大小为θ∈[0,1]。每个Fc节点代表一个类别,Fc节点的输出代表Ah在输出类别k中的适合程度。Fb和Fc节点之间的连接是二进制值来表示。
1.1.1隶属度函数
当提供新的训练样本时,FMMN使用隶属度函数,其取值范围为0~1,用于表示样本相对于超盒的拟合度,查找最匹配的超盒。隶属度函数使用式(2) 计算[2]:
max(0,1-max(0,γmin(1,vji-ahi)))]
(2)
式中:Bj表示第j个超盒;Ah=(ah1,ah2,…,ahn)∈In是第h个输入样本,并且γ是一个灵敏度参数,用于调节隶属函数随着Ah与Bj之间的距离增加而减小的速度。
1.1.2扩展规则
在训练阶段,执行超盒扩展过程以将输入数据包括在各自的超盒中。当超盒Bj扩展为包括输入模式Ah时,必须满足以下约束[2]:
(3)
如果输入数据不属于任何超盒,即不满足式(3)中的约束,则创建了一个新的超盒以便输入数据被网络学习。如果输入数据满足式(3)中的扩展要求,则通过式(4)更新该超盒。公式如下:
(4)
1.1.3重叠测试
重叠测试是确定是否有不同类别的重叠的超盒。由于扩展过程中可能会导致现有超盒之间存在重叠的情况,所以需要通过测试来确定是否存在重叠。这个测试主要考虑以下4种情况[2]。如果满足其中任意一个情况,就认为超盒之间存在重叠。
情况1:
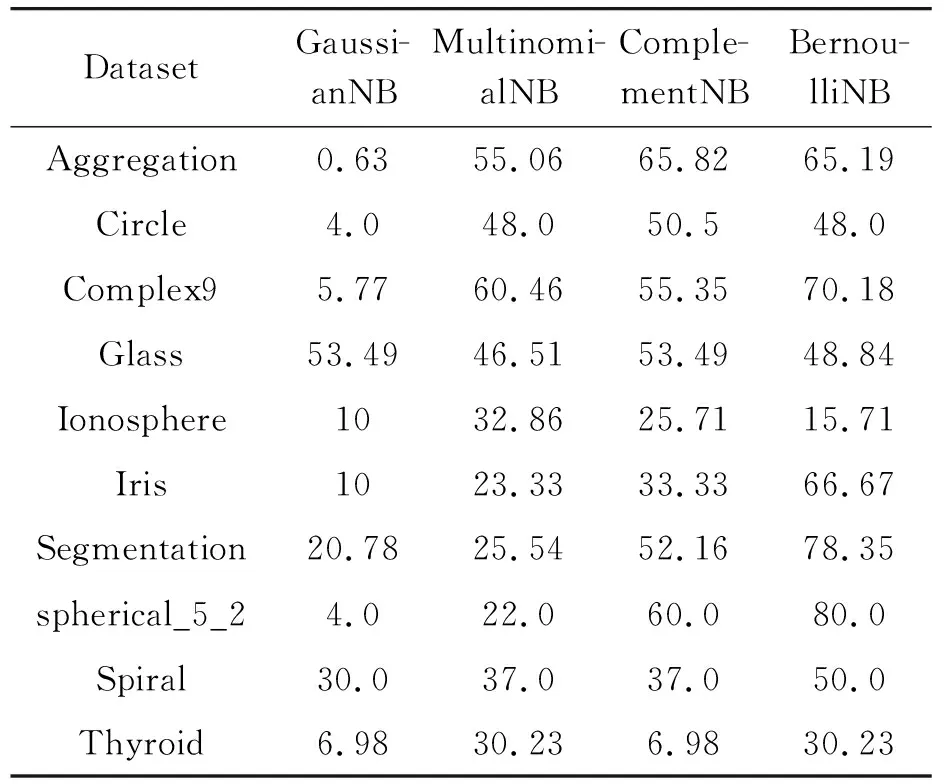
Vji (5) 情况2: Vki (6) 情况3: Vji min(min(Wki-Vji,Wji-Vki),δold) (7) 情况4: Vki min(min(Wji-Vki,Wki-Vji),δold) (8) 最初假定δold=1。如果δold-δnew>0,则Δ=i&δold=δnew。这表明重叠检测到第一个维度,测试继续进行下一个维度。如果不存在其他重叠区域,则测试停止,并通过设置Δ=-1,即将下一个收缩步骤表示为“不必要”[12]。注意,相同类别的超盒可以存在重叠。 1.1.4收缩规则 如果来自不同类别的超盒存在重叠,则会启动超级框收缩过程以消除重叠的区域。在收缩过程中,通过仅调整每个重叠的超级盒中n个维度中的一个维度来保持超级盒尺寸尽可能大。即,通过最小化调整每个超级框来消除重叠区域。 增强的模糊最小最大神经网络主要在扩展规则、重叠测试以及收缩方面进行了改进。 在扩展规则方面,为了解决现有FMMN扩展过程中可能会导致后续过程中的不同类的超盒超范围扩展这一难题[13]。Mohammed 等[4]提出如下的新扩展规则: maxn(Wji,Ahi)-minn(Vji,Ahi)≤θ (9) 根据式(9),第j个超级框的每个维度都经过独立测试,以调节其是否超过扩展系数(θ)。当所有超盒尺寸不超过θ时使用扩展。 在重叠测试和收缩方面,在超盒重叠测试期间,使用FMMN模型中给出的当前4种情况不足以识别整个覆盖范围。为了解决此难题,Mohammed 等[4]进一步完善了重叠测试的情况,将重叠测试和收缩由4种情况修改为如下的9种情况: 情况1: Vji δnew=min(Wji-Vki,δold) (10) 情况2: Vki δnew=min(Wki-Vji,δold) (11) 情况3: Vji=Vki δnew=min(min(Wji-Vki,Wki-Vji),δold) (12) 情况4: Vji δnew=min(min(Wji-Vki,Wki-Vji),δold) (13) 情况5: Vki=Vji δnew=min(min(Wji-Vki,Wki-Vji),δold) (14) 情况6: Vki δnew=min(min(Wji-Vki,Wki-Vji),δold) (15) 情况7: Vji δnew=min(min(Wji-Vki,Wki-Vji),δold) (16) 情况8: Vki δnew=min(min(Wji-Vki,Wki-Vji),δold) (17) 情况9: Vki=Vji δnew=min(Wki-Vji,δold) (18) 为了避免在获胜超盒附近产生过多的小超盒,Mohammed等[5]提出了K最近邻模糊最小最大神经网络。该模型与原始FMMN仅关注一个获胜的超盒不同,该模型选择了K个具有相同类别标签的超盒来确定超盒扩展过程最终获胜的超盒,这样能够避免在获胜超盒附近产生过多的小超盒,从而降低FMMN网络复杂度。同时,该模型可以应用于FMMN的多种变体,包括增强模糊最小最大神经网络,形成K最近邻增强模糊最小最大神经网络(KEFMMN)。 首先,选择获胜的超盒(具有最高隶属函数的超盒),然后,使用式(3)将其所有维度与扩展系数进行比较。获胜的超盒对式(3)的任何违反都会导致选择下一个最近的超盒,以通过相同的检查步骤。如果所有K最近邻超盒都不能满足式(3),则将创建一个新的超盒来对输入样本学习。通过这种方式,能够避免在获胜超盒附近创建过多的小型超盒,从而降低了网络的复杂度。 FMMN及其变体在训练网络的时候没有考虑超盒内部训练数据的分布情况,并且考虑扩展系数的问题也不是很充分,导致每次训练新数据集都要重新选择最优的扩展系数。E-CFMM通过增加数据质心来表示超盒内部训练数据的分布情况,通过集成的方法来解决选择扩展系数的问题。第一,每个超盒增加了数据质心,在扩展规则、收缩规则以及预测的时候都考虑了数据质心的问题;第二,增加了删除同类型超盒的步骤,以便减少网络复杂度;第三,通过集成的方法解决了传统的FMMN及其变体选择最优扩展系数的问题。具体如下。 当输入为第1个训练数据或者没有满足扩展要求而要单独形成超盒的数据时,此时形成的超盒,如式(19)所示: Vji=Wji=Cji=ahi,(i=1,2,…,n) (19) 式中:ahi是第h个数据样本的第i维度值;j为第j个超盒,i样本的维度。 当输入的数据满足扩展超盒,则通过递推算术平均法进行更新质心值,如式(20)所示[14]: (20) 在训练模糊最小最大神经网络时,选择获胜的超盒不仅依靠隶属度而且还考虑输入的样本点与超盒数据质心之间的距离,具体设计如下: 当输入的样本点位于相同类别的超盒隶属度为1时,即输入的样本点完全位于某个相同类别的超盒内,这时不考虑输入样本点与超盒内的数据质心之间的距离。当输入的样本点位于相同类别的超盒隶属度不为1时,则考虑样本点与这些超盒数据质心之间的距离。样本点与质心之间距离的计算公式采用欧式距离计算,具体计算如式(21)所示。 (21) 式中:n为输入样本的维度;x表示输入的样本;y表示超盒数据质心。 在计算完具体的距离以后,需要将其转换为具体的距离权值。计算方法如式(22)所示。 (22) 式中:m为相同超盒的个数;dist为式(21)计算的结果。 在选择最终获胜的超盒时,将每个超盒的隶属度的值(由式(2)所求)与其距离权值相加,用相加后的值由大到小排序超盒,选择前K个获胜超盒,并进行下一步的扩展判断。 从3.2节选择的K个获胜的超盒中,选择第1个超盒进行扩展条件判断,如果满足扩展条件,则进行重叠测试。如果存在重叠则进行收缩,收缩的规则如表1所示。其中情况1、2以及情况4都考虑了质心是否在重叠区域的问题。并且在每个收缩后的超盒都增加一个长度为0.01单位的间隔,这样可以避免输入的样本点刚好落在2个重复超盒收缩的边界。 表1 E-CFMM的收缩规则 续表(表1) 续表(表1) 通过表1的方式收缩存在重叠的超盒后,还要判断本次超盒收缩得是否过多,当收缩不到原来超盒大小的1/3时,则拒绝本次收缩并选择下一个候选超盒进行扩展和收缩判断,如果所有的候选超盒都不满足上述情况,则样本点单独形成一个超盒。当收缩大于原来超盒大小的1/3时,则还要判断收缩后的超盒的数据质心还在不在超盒内,如果不在,则需要使用如下的方法更新质心: 如果超盒数据质心小于该超盒的下限V,则该质心独立形成一个超盒,并将原来的超盒所隶属的样本数量与质心形成的超盒所隶属的样本数量平分,原来的超盒数据质心设置为超盒的下限V。 如果超盒数据质心大于该超盒的上限W,则该质心独立形成一个超盒,并将原来的超盒所隶属的样本数量与质心形成的超盒所隶属的样本数量平分,原来的超盒数据质心设置为超盒的上限W。 由于利用重叠测试值来判断不同类别的超盒之间是否存在重叠时,可能会导致同类超盒存在完全被包住的情况,如果不删除被完全包住的超盒的话不但不会提升模型的准确率而且还可能会增加网络的复杂度。为此,增加删除同类完全被包住的超盒的方法,并更新较大超盒的质心以及超盒样本数量。更新质心的方法见式(23),更新超盒样本数量方法见式(24)。 (23) cardin_parent=cardin_parent+cardin_current (24) 式中:cardin_parent表示较大超盒所拟合的样本数量;cardin_current表示较小超盒所拟合的样本数量;cluster_parent表示较大超盒的数据质心;cluster_current表示较小超盒的数据质心。 第1步,训练弱分类器。首先,选择5个带质心的K最近邻增强模糊最小最大神经网络作为弱分类器,扩展系数分别为0.1、0.3、0.5、0.7、0.9。其次,打散训练集,将训练集平分,其中前一部分训练集用于训练弱分类器,而后一部分训练集用于通过训练好的弱分类器来进一步生成训练数据。复次,每个弱分类器随机选择前一部分训练集中的1/3的数据用于训练初始网络,再随机选择1/3的训练样本测试第一个弱分类器,并保留预测错误的样本,测试之后用这些数据训练第一个弱分类器。再次,在错误的样本中添加新的训练样本,使得数量等于训练样本的1/3,并将该数据用于测试第2个弱分类器,进行上面同样的操作。如果是第5个弱分类器产生的预测错误的样本,则留给第1个弱分类器进行训练使用。当某个弱分类器预测错误率为0或者在3轮中最小错误率没有改变时,则停止训练该弱分类器。最后,当没有可以训练的弱分类器时,则停止训练,进行下一步的操作。 第2步,形成随机森林所需要的新的数据。训练完成弱分类器之后,使用后一部分训练集和测试集用于刚刚训练好的弱分类器形成新的样本,此时每个弱分类器输出10个离散属性值,分别为: 该超盒预测的类别值。 测试样本所属的超盒的样本的数量。 求得测试样本中最高隶属度相同类别的超盒个数。 求得测试样本中最高隶属度不同类别的超盒个数。 测试样本与数据质心之间距离最小的超盒类别,如果多个选择第1个。 求得测试样本中最大隶属度所属的类别,如果多个选择第1个。 测试样本最大隶属度是否为1。 测试样本点与超盒数据质心之间距离最近的5个超盒所属类别中,类别相同个数最多的类别,如果多个选择第1个。 测试样本点所求得的前5个最大隶属度所属类别中,类别相同个数最多的类别,如果多个选择第一个。 测试超盒的正确率,其正确率转换为0~10个等级,等级越大正确率就越大,其中使用的数据为训练弱分类器的数据。 第3步,数据预处理。首先,将每个弱分类器输出的10个离散属性值进行拼接组成拥有50个条件属性和1个决策属性的数据。其次,使用信息增益与属性依赖度进行特征选择,选出信息增益与属性依赖度之和大于零的特征。最后,进行标准归一化。其中,信息增益计算方法参见式(25),属性依赖度计算方法参见式(26)。 (25) 式中:a为离散属性,有V个可能的取值{a1,a2,…,aV};Dv表示所有在属性a上取值为aV的样本。Ent(D)计算方法参见式(27)。 (26) 式中:U为论域;PosB(D)表示正域,其计算方法参见式(28)。 (27) 式中:i表示第i类样本所占的比例为pi(i=1,2,…,N)。 (28) 本文中,X为依据决策属性划分的数据集,R为一个条件属性,U为整个数据集,Y为依据R的值划分的数据集。 第4步,训练并测试随机森林。将这些整理好的训练数据作为随机森林的训练数据,将整理好的测试数据作为随机森林的测试数据,最后输出预测结果。 实验部分使用UCI资料库中的数据集[15]。这些基准数据集已被广泛用于评估机器学习算法。数据集的详细信息如表2所示。在以下实验中,所有数据集中的训练数据与测试数据之比为8∶2。 表2 实验数据集 为了进一步比较E-CFMM与其他算法的性能,使用准确度、精确率、召回率以及F-score,并使用ROC曲线和AUC值以及箱型图的方式来做性能评估指标分析。表3为由二分类问题定义的混淆矩阵表。 表3 混淆矩阵 准确度定义如下: Accurate=(TP+TN)/(TP+TN+FN+FP) (29) 精准率定义如下: (30) 召回率是分类器正确检测到正类实例的比率,其计算公式如下: (31) 根据精准率和召回率的计算结果,F-score的公式定义如下: (32) 此外,AUC得分是根据ROC曲线下的面积来测量的,该曲线根据真实阳性率(TPR)和错误阳性率(FPR)绘制。 TPR=TP/(TP+FN) (33) FPR=FP/(FP+TN) (34) 为了比较FMMN、EFMNN、KNEFMNN以及CFMM之间的准确度和运行时间。在实验中使用3种不同尺寸的扩展系数,即小尺寸θ=0.1,中等尺寸θ=0.55和大尺寸θ=1.0。其他参数设置为K=2,γ=1。比较结果如表4所示。 通过表4可以看出:在不同扩展系数下,CFMM在准确率方面都是最好的。同时,相比于其他模糊最小最大神经网络方法,CFMM在准确率方面随着扩展系数θ=1的增大而更有优势。但CFMM在训练时间方面比其他方法耗时要多,特别是在小尺寸的扩展系数的时候。导致CFMM训练时间长的根本原因在于增加了计算质心和更新质心这2个步骤所消耗的时间。导致CFMM的准确率随着扩展系数θ=1的增大而增大的根本原因在于扩展系数越大,超盒扩展的越“粗糙”,而考虑了质心以及新的收缩规则的情况会使得超盒扩展得更加准确。 表4 CFMM与FMMN、EFMNN、KNEFMNN在不同扩展系数下的实验结果 由于FMMN及其变体需要考虑扩展系数选择的问题,而E-CFMM不需要考虑扩展系数的问题,为了更直观地表现实验结果,对准确度、精准率、召回率以及F-score进行比较。因为评估指标只适用于二分类的情况,因此使用Circle、Ionosphere和Spiral数据集作为比较的数据集。此处,FMMN及其变体的扩展系数与E-CFMM中的弱分类器的扩展系数相同,即扩展系数分别选择0.1、0.3、0.5、0.7、0.9,而E-CFMM采用运行5次的结果作为比较结果。其中K=2,γ=1。箱型图比较结果见图2~4。 图2 E-CFMM与FMMN及其变体 在Circle数据集上的比较结果 图3 E-CFMM与FMMN及其变体 在Ionosphere数据集上的比较结果 图4 E-CFMM与FMMN及其变体 在Spiral数据集上的比较结果 通过箱型图的比较可以发现,E-CFMM算法每次运行的结果在准确度、精准率、召回率以及F-score方面大部分优于FMMN及其变体,并且E-CFMM不受到扩展系数选择的影响。这主要是因为不同的数据集在使用训练好的每个带有不同扩展系数的弱分类器生成数据时,最接近拥有最优扩展系数的弱分类器生成的条件属性在使用随机森林训练时,该条件属性会有更高的信息增益率,即越接近拥有最优扩展系数的弱分类器生成的条件属性越重要。 删除同类完全包住的超盒对E-CFMM的影响,如表5所示。 表5 比较删除同类完全包住的超盒对E-CFMM的影响 虽然同类超盒可能有一些其他有用信息,但通过表5可以发现,删除同类完全包住的超盒对E-CFMM几乎没有影响。导致这个现象的原因是因为集成方法有更好的泛化能力。 在分类性能方面,E-CFMM与其他流行的机器算法(如朴素贝叶斯、K最近邻、支持向量机和随机森林)进行了比较,其中支持向量机使用了径向基函数(RBF)内核。此处,直接利用了scikit-learn工具箱[16]的这些机器学习算法,所有的参数都使用默认值,对于具有随机性的算法,采用运行5次取平均值的方法来表示预测结果。最终实验结果如表6所示。 表6 E-CFMM与其他机器学习的实验结果比较 通过表6发现,如果从最小错误率的个数来看,所提出来的算法(E-CFMM)与随机森林的性能差不多,相比于其他的机器学习算法来说最优结果的个数最多。 为了更全面地比较E-CFMM与其他机器学习方法的分类性能,此处采用假设检验来进行测试。零假设是:H0: 10个不同的实验数据集中,E-CFMM与流行的机器学习算法的性能上没有差异。为了拒绝这个假设,在本次实验使用Friedman秩和检验用作测试多个方法之间的显著性差异。首先,Friedman秩和检验对分类算法的性能进行排名,其中最佳分类器被分配为第1等级,第2个最佳分类器被分配为第2等级,依此类推。最后,Friedman检验对分类器的平均等级进行比较。表7显示了E-CFMM与流行的机器学习算法的测试误差等级以及10个数据集中的平均等级。 表7 E-CFMM与流行的机器学习算法的测试误差等级 以及10个数据集中的平均等级 如果实验结果满足零假设的话,则说明所有算法的执行情况相似,因此它们的平均秩Rj应该相等,弗里德曼(Friedman)统计量计算参见式(35): (35) (36) 该度量根据具有k-1和(k-1)·(N-1)自由度的F分布进行分配。如果否定假设被拒绝,即模糊最小最大神经网络的性能在统计上不同,则需要进行事后检验,以便发现这些模型的平均等级之间的关键差异。 使用95%置信区间(α=0.05)作为识别模糊最小最大神经网络的统计意义的阈值,使用弗里德曼检验计算出F分布: 本次实验具有10个数据集和5个分类器,FF根据F分布具有分布5-1=4和(5-1)×(10-1)=36自由程度,F(4,36)的显著性水平的临界值α=0.05是2.634。观察到FF>F(4,36),因此原假设被拒绝。这也就意味着在所考虑的数据集上, E-CFMM与流行的机器学习算法的性能上有差异。 下面比较E-CFMM算法与其他机器学习算法的性能指标,如表8~10所示,算法的ROC曲线结果见图5。 表8 在Circle数据集上各种机器学习算法的精准率、召回率和F-score 表9 在Ionosphere数据集上各种机器学习算法的精准率、召回率和F-score 表10 在Spiral数据集上各种机器学习算法的精准率、召回率和F-score 通过表8~10可以发现,E-CFMM算法在Ionosphere数据集以及Spiral数据集上无论是在精准率、召回率以及F-score方面都表现的最优。同时,通过图5可以发现,E-CFMM算法在Circle数据集和Spiral数据集中AUC表现也是最优的。 图5 不同算法在不同数据集表现的ROC曲线 为了使得实验结果更具有参考价值,增加对机器学习方法的重要参数的比较实验。表11~14展示了不同参数下的朴素贝叶斯、KNN、SVM和RF的性能,表中字体加粗的表示其性能优于E-CFMM。 通过表11~14可以发现:当随机森林的n_estimators设置为100时与E-CFMM的性能不相上下,其他的参数的机器学习方法的性能都略低于E-CFMM,尤其是朴素贝叶斯在准确率方面大部分结果都是低于E-CFMM。 表11 不同版本的朴素贝叶斯的性能 表12 不同参数下的KNN性能 表13 不同参数下的SVM性能 表14 不同参数下的RF性能 提出了一种带质心的K最近邻增强模糊最小最大神经网络的集成网络方法(E-CFMM),通过实验发现:E-CFMM可以有效地克服FMMN及其变体过于依赖扩展系数的选择问题而且还提升了准确度,并且通过箱型图的分析看出,E-CFMM算法每次运行的结果在准确度、精准率、召回率以及F-score方面大部分是优于FMMN及其变体。同时,可以发现E-CFMM测试误差平均等级是1.95,这在其他机器学习方法的测试误差平均等级中是最低的。1.2 增强的模糊最小最大神经网络(EFMMN)
1.3 K最近邻模糊最小最大神经网络(KFMMN)
2 带质心的K最近邻增强模糊最小最大神经网络的集成方法
2.1 增加超盒的数据质心

2.2 扩展规则
2.3 收缩规则



2.4 删除同类完全被包住的超盒
2.5 集成方法
3 实验结果及分析
3.1 数据集
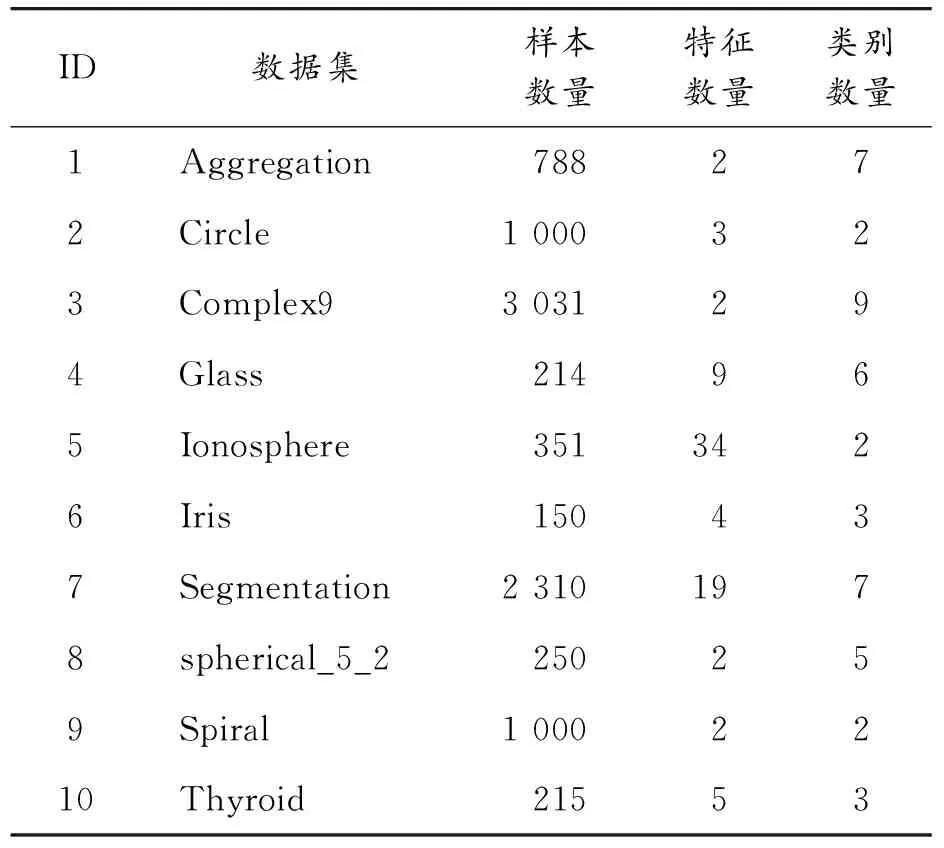
3.2 性能评估指标

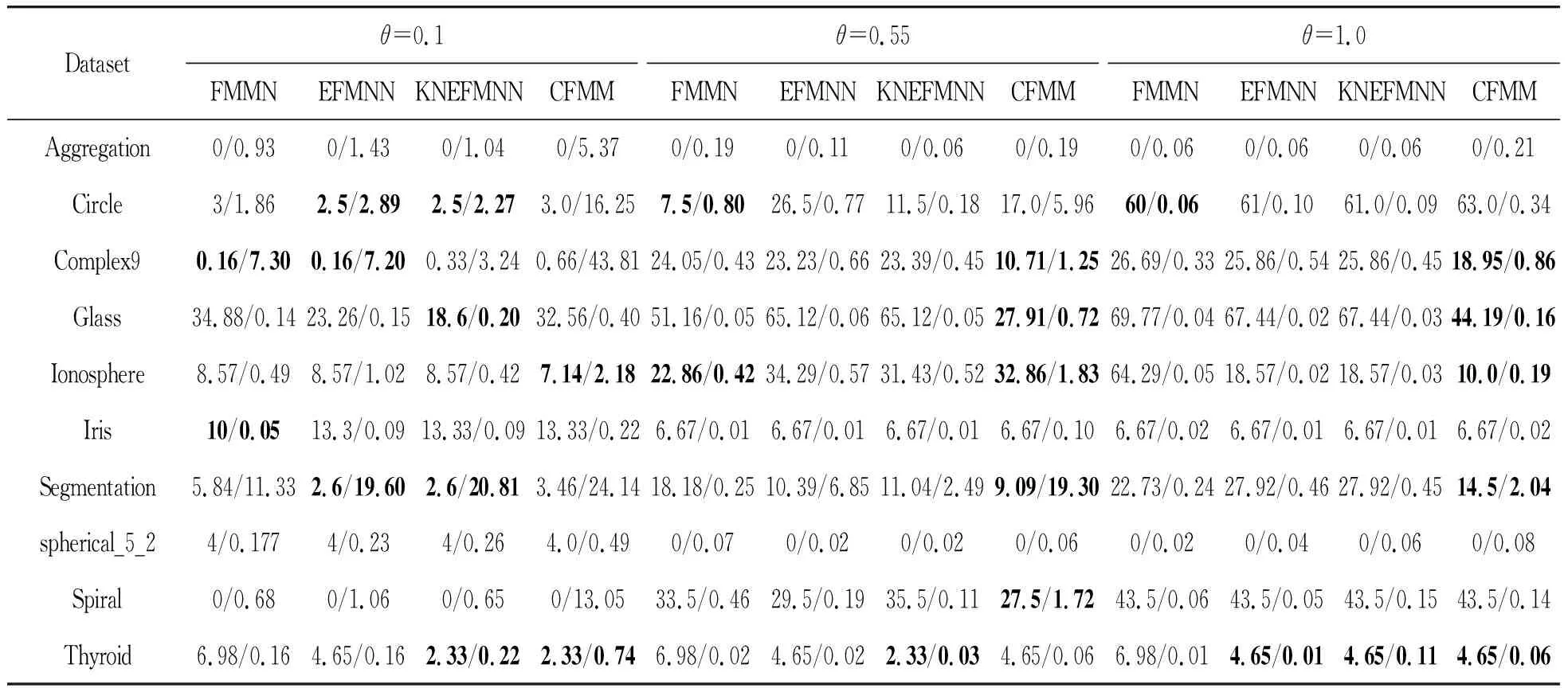
3.3 带质心的K最近邻增强模糊最小最大神经网络(CFMM)与其他模糊最小最大网络的比较
3.4 E-CFMM与其他模糊最小最大网络的比较



3.5 删除同类完全包住的超盒对E-CFMM的影响

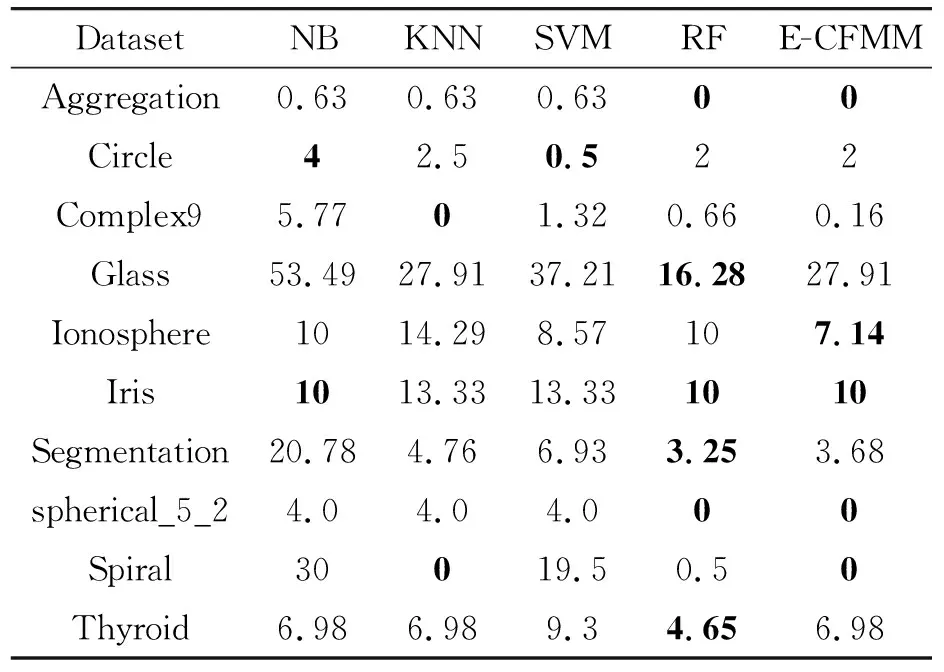
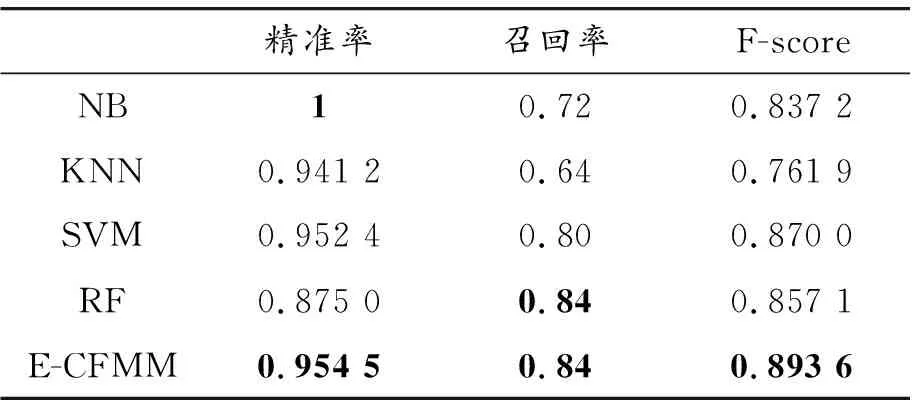
3.6 E-CFMM与其他机器学习算法的比较








4 结论
