燃料电池客车驱动系统建模及能量管理策略优化研究

2021-10-19严正峰王浩琳吴景铼

重庆理工大学学报(自然科学) 2021年9期

严正峰，王浩琳，，吴景铼，张农

(1.合肥工业大学汽车与交通工程学院，合肥 230009； 2.合肥工业大学汽车工程技术研究院，合肥 230009)

燃料电池是一种清洁、高效的能量源，具有极大的发展潜力[1-4]，整车经济性和电池寿命等是制约其商业化发展的关键因素[5]。燃料电池输出功率的响应速度较慢，因此，通常需要与动力电池配合满足整车动力需求的快速响应，即通过燃料电池-动力电池混合动力驱动整车。燃料电池混合动力汽车的关键技术之一是制定合理的能量管理策略，通过对整车的能量管理策略进行合理的设计，提高燃料电池的工作效率，提升客车的经济性，增加燃料电池的使用寿命等[6-7]。

燃料电池汽车的能量管理策略可主要概括为基于规则的控制策略和基于优化的控制策略[8]。基于规则的能量管理策略是目前商业化应用最普遍的控制策略，其思想是根据动力电池SOC状态控制燃料电池输出功率，以达到维持动力电池SOC和减少系统能耗的目的。这种控制策略的效果往往与设计人员的经验有很大的关系，无法保证燃油经济性达到最优[9-10]。基于优化的控制策略可分为瞬时优化和全局优化，基于全局优化的DP策略可以实现最优[11]，但由于计算量大且需要未来工况作为输入条件，较难应用到实际行驶中。

本文提出2种结合规则和优化算法的能量管理策略，对控制规则通过优化算法进行改进。目前对于燃料电池能量管理策略的研究大多数都以经济性为目标[12]，缺少考虑燃料电池寿命的能量管理策略研究。本文将模糊控制策略与遗传算法相互结合，既运用了模糊控制不过于依赖精确数学模型的优良特点，又结合了遗传算法的寻优能力。同时利用序列二次规划算法对基于简单规则策略进行了优化，取得了良好的效果。当前的研究多数是基于某种单一工况的仿真研究，但对于实际行驶而言，单一工况下整车运行时间较短，很难验证控制策略的稳定性，难以观察到整车在长时间运行下动力电池SOC的维持状态和整车的能耗情况。本文在中国典型城市公交工况的基础下，对20个重复工况进行仿真，避免了单工况仿真的局限性，更符合整车实际运行状态。结果显示：优化后的2种控制策略不仅在整车经济性方面优于未经改进的模糊控制策略，而且避免了燃料电池输出功率的瞬时大幅度波动，有助于延长燃料电池的使用寿命。

1 燃料电池客车动力系统建模

燃料电池混合动力客车驱动系统的关键部件包括储氢罐、燃料电池堆、DC/DC转换器、动力电池、电机控制器、驱动电机、机械传动系统等，动力系统如图1所示。车辆建模时需要构建多个系统，考虑不同的系统之间的相互联系，模型较为复杂，涉及到许多参数。本文研究重点为燃料电池能量管理策略的制定，因此选取后向建模的方法，简化建模步骤，去掉驾驶员模型，由已知工况代替。对电机及电池等复杂系统侧重于效率的模型，合理运用已有的实验数据，在显著简化了建模步骤的同时缩短了仿真时间。本文后向仿真整车能耗模型主要包括燃料电池的效率模型、电机能耗模型、动力电池等效电路模型、整车纵向动力学模型等。

图1 燃料电池客车动力系统示意图

1.1 燃料电池模型

燃料电池模型的准确建立需要复杂的建模和大量的数据。对于整体模型来说，只需要了解燃料电池输出功率与效率的关系。为了保证模型的准确性同时降低建模复杂程度，通过项目方提供的数据，拟合得出燃料输出功率与效率的曲线，如图2。由图可知，制定的能量管理策略要想保证燃料电池的高效率，输出功率应在5～30 kW。

图2 燃料电池的功率-效率曲线

1.2 动力电池模型

动力电池由192个单体电池组成，对于动力电池的建模采用Rint等效电路[13]，如图3所示。

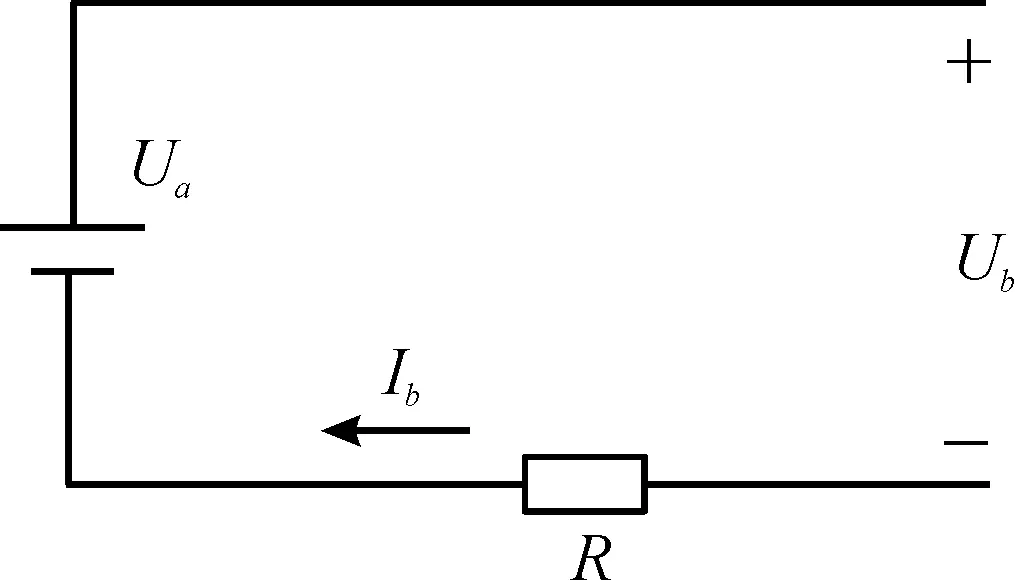
图3 动力电池Rint等效电路示意图

从图3可以得到，动力电池等效电路中电流Ib和输出功率Pb存在以下关系：

(1)

式中：Ua为动力电池开路电压；Ib为动力电池输出电流；Pb为动力电池输出功率；R为动力电池内阻。

电池的母线电压Ub可由下式所得：

Ub=Ua-IbR

(2)

动力电池荷电状态(SOC)作为能量管理的重要参数，每一时刻的SOC数值可由下式得到：

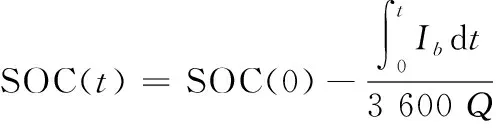
(3)

式中：SOC(t)表示当前t时刻的动力电池SOC值，SOC(0)表示动力电池初始时刻的SOC值，Q表示动力电池的容量。

动力电池的内阻R和开路电压Ua均可由电池的SOC确定，内阻R和开路电压Ua随电池的SOC变化如图4所示。

图4 内阻和开路电压Uoc与电池的SOC关系曲线

1.3 等效能耗模型

燃料电池客车在行驶时不仅仅依靠燃料电池提供能量，动力电池也参与到工作中。因此，在计算氢耗时，不能仅仅计算燃料电池自身消耗的氢气，还应该考虑动力电池消耗的电能，对此本文引入一个等效能耗概念。行驶过程中整车消耗氢气等同于整车消耗能量的转换，因此，直接采用等效能量消耗代替等效氢耗，氢耗最小即消耗能量最小。对燃料电池而言，燃料电池的能量消耗用下式表达：

(4)

动力电池的等效能量消耗计算如下：

(5)

整车等效能耗计算为：

WR=WFC+WB

(6)

式中：WFC为燃料电池消耗能量(J)；PB为动力电池输出功率(W)；PFC为燃料电池输出功率(W)；ηFC为燃料电池的效率；WB为动力电池消耗能量(J)；WR为整车等效能耗(J)。

1.4 整车动力学模型与电机模型

燃料电池混合动力客车在行驶时受滚动阻力、坡度阻力、空气阻力、加速阻力的外力作用，其动力学方程为[14]：

(7)

式中：Tr为施加在车轮上的转矩；r为车轮半径；m为整车总质量；g为重力加速度；f为滚动阻力系数；α为爬坡坡度；δ为汽车旋转质量换算系数；v为车速(m/s)；ρ为空气密度；A为迎风面积；CD为空气阻力系数。

在驱动模式下，车辆的驱动力全部由电机提供。而在制动方式下，制动力由电动机和摩擦制动器提供。电机制动能量再生策略为当车速大于10 km/h时，40%的制动力由电机提供。当车速低于10 km/h时，由于效率较低，电机不再生制动能量。因此，电机转速和转矩按下式确定：

(8)

(9)

式中：ω为电机转速(r/min)；i为传动比；T为电机转矩(N·m)。

电机特性通常用效率映射来描述，但当电机转矩和转速较低时，效率映射存在空白区域。为了解决这一问题，将效率映射转换为功率损耗映射，根据效率图计算功率损耗图的具体方法可参考文献[15]。功率损耗曲线如图5，其中红色曲线表示电机的最大输出转矩随转速的变化。

图5 电机损耗功率曲线

电机实际消耗功率为：

(10)

式中：PR为电机实际消耗功率；PS为电机损耗功率(W)。

驱动系统建模中所用的参数如表1所示。

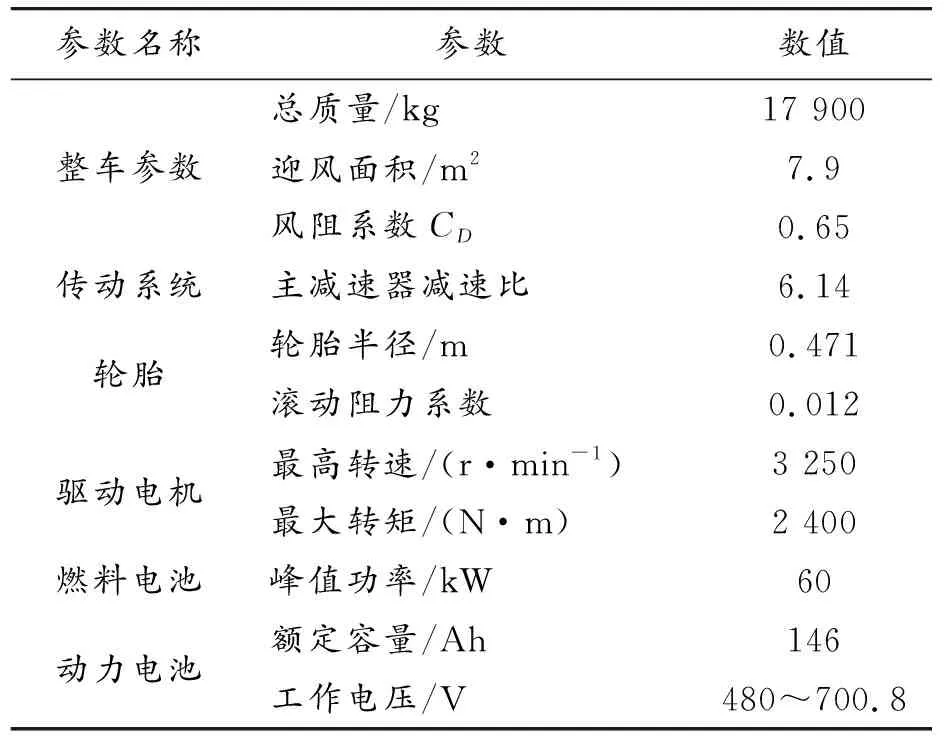
表1 整车动力系统参数

2 能量管理策略

2.1 能量管理策略目标

在分配燃料电池和动力电池的能量时，需要满足以下要求：

1) 动力电池的SOC需要维持在合理区间内，并且在低SOC时可由燃料电池充电，高SOC时可放电保持SOC的平衡。

2) 保证整车能耗较低，提高整车能耗的经济性。

3) 减少燃料电池输出功率的大幅度变化，延长燃料电池的使用寿命。

2.2 基于遗传算法优化的模糊控制能量管理策略

2.2.1模糊控制器的设计

模糊控制器选取2个参数作为输入变量：第1个是整车动力系统需求的总功率PR，第2个是当前动力电池的SOC。经计算整车动力系统需求总功率论域为[-70，250]kW，动力电池SOC论域为[0，1]。输出变量为燃料电池需求功率PFC，动力电池输出功率PB则提供剩余的功率需求，按下式计算：

PB=PR-PFC

(11)

由模糊控制理论，定义输入变量总功率PR模糊子集为{NB，NS，Low，Medium，High}，定义动力电池SOC的模糊子集为{L1，L2，Medium，H1，H2}，定义输出变量PFC的模糊子集为{L1，L2，Medium，H1，H2}，隶属函数选取三角形函数与梯形函数相结合的形式。其中输入变量PR横轴的坐标为[-16，24.5，65，105.5，146]kW，SOC的坐标为[0.2，0.35，0.5，0.65，0.8]，输出变量PFC的坐标为[12，21，30，39，48]kW，输入输出参数各个参数的隶属函数分布曲线如图6所示。

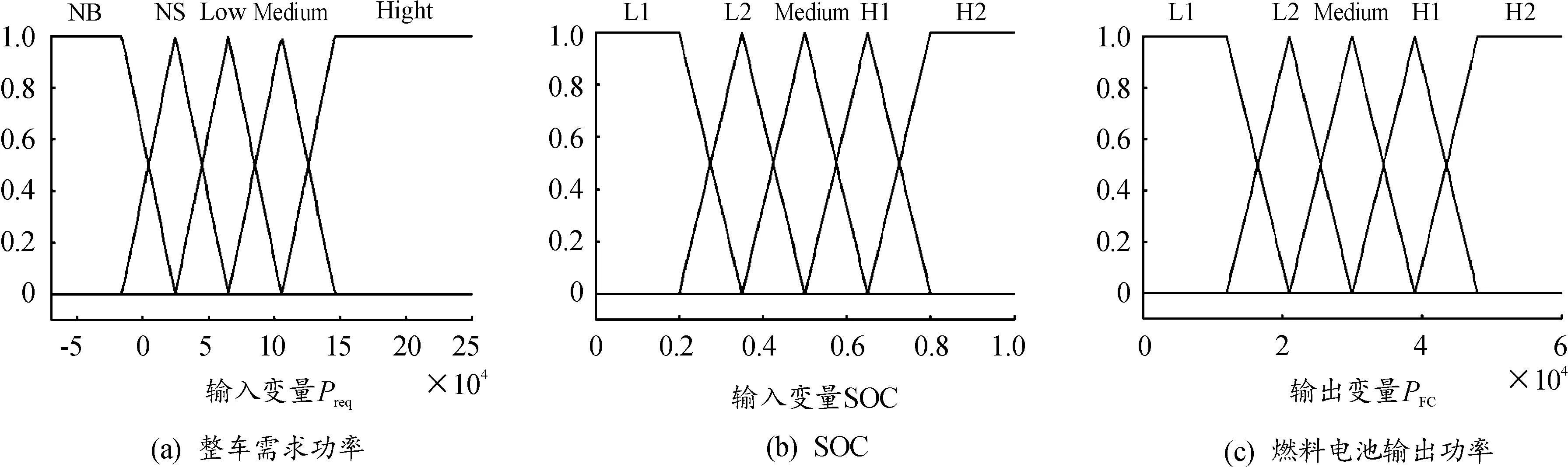
图6 模糊隶属函数分布曲线

模糊规则的制定需要满足以下条件：

1) 动力电池SOC过高时，在不影响动力性的前提下，燃料电池输出功率尽可能降低，此时整车功率主要由动力电池提供，通过放电让SOC降低到合理范围。

2) 动力电池SOC中等时，根据整车需求功率大小，调整燃料电池输出功率，让其尽可能跟随整车需求功率，以保证动力电池的SOC在正常范围波动，此时燃料电池和动力电池应共同提供整车功率。

3) 动力电池SOC过低时，燃料电池应以高功率状态输出，此时不仅需要提供整车需求功率，也要给动力电池充电，保证动力电池SOC在规定范围内，若整车需求功率过大，则燃料电池以最大功率输出。

模糊控制器整体功率分布如图7所示。

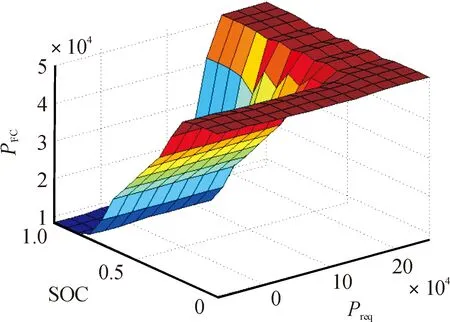
图7 模糊控制器整体功率分布曲面

2.2.2适应度函数的选取

以上给定的模糊控制器的坐标节点通常并非最优，现使用遗传优化算法对这些坐标节点进行优化设计。优化目标为整车等效能耗，同时减小燃料电池输出功率的变化频率，选取的适应度函数为：

(12)

式中：x为对设计变量进行编码后的染色体对应序号；α为惩罚系数，本文取值分别为α1=3×105，α2=3×107，α3=5 000；fi为与燃料电池输出功率变化率和电池SOC相关的惩罚函数，定义为：

(13)

(14)

(15)

式中：SOC0表示电池初始SOC值，取0.7；c为一个较小的SOC变化值，取0.01。

通过构造的适应度函数可以看出，适应值F(x)与整车能耗WR成反比，整车能耗越小适应值越大，满足在遗传算法中适应值越大的个体遗传到下一代的概率更大的条件。

2.2.3遗传算法编码及运行参数的设定

考虑到编码精度不超过0.01，对坐标X1…X5代表的输入变量PR用15位2进制数表示，对坐标X6…X10代表的输入变量SOC用10位2进制数表示，对X11…X15代表的输出变量PFC用13位2进制数表示，生成长度为5×15+5×10+5×13=190的二进制字符串，每一个字符串代表一个染色体，确定初始种群的大小为190，生成190×100大小的二进制矩阵。在编写遗传算法时，预先设定相关参数如表2所示。

表2 相关参数

2.3 基于规则的能量管理策略的优化

基于规则的能量管理策略是目前商业化应用最普遍的控制策略，其思想是根据动力电池SOC状态控制燃料电池输出功率，以达到维持动力电池SOC和减少系统能耗的目的。燃料电池输出功率与动力电池SOC状态之间的关系是影响该控制策略性能的关键。本文将采用最简单的控制规则，即通过多段线性函数描述燃料电池输出功率与动力电池SOC之间的关系，如图8所示。

图8 燃料电池输出功率与SOC关系曲线

由于期望动力电池SOC维持在[0.6，0.8]，因此，定义这2个点对应的燃料电池输出功率PFC1和PFC2为设计变量。当动力电池SOC在此区间变化时，燃料电池输出功率通过插值得到。当动力电池SOC低于0.6时，需要更加快速地提升燃料电池输出功率，因此对应的线性函数斜率将增加，记为k1。当动力电池SOC高于0.8时，燃料电池输出功率需要进一步降低，此段线性函数斜率采用k2描述。当PFC1、PFC2、k1和k2确定之后，控制规则即被制定。为减少系统能耗，可通过优化方法确定4个变量值。本文采用序列二次规划方法，使用Matlab中的优化函数对这4个变量进行设计。

3 仿真分析

3.1 优化的能量管理策略

以中国典型城市公交工况(图9)作为燃料电池客车的运行条件，对模糊控制策略和基于规则的控制策略进行优化。

图9 中国典型城市公交工况曲线

经遗传算法优化后的输入输出参数的模糊隶属函数曲线如图10所示。

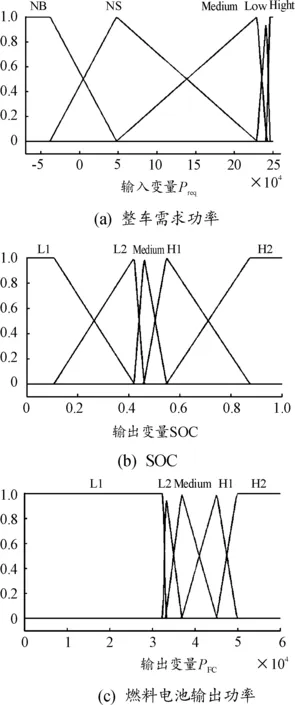
图10 优化后的隶属函数分布曲线

优化后的基于规则的能量管理策略的控制规则如下：PFC1=33.0 kW，PFC2=3.1kW，k1=-110.6 kW，k2=-95.6 kW，如图11所示。

图11 优化后燃料电池输出功率与电池SOC的关系曲线

3.2 能量管理策略对比

分别将模糊控制策略、经过遗传算法优化后的模糊控制策略、基于规则式的能量管理策略进行对比，3种能量管理策略对应的SOC变化如图12所示。

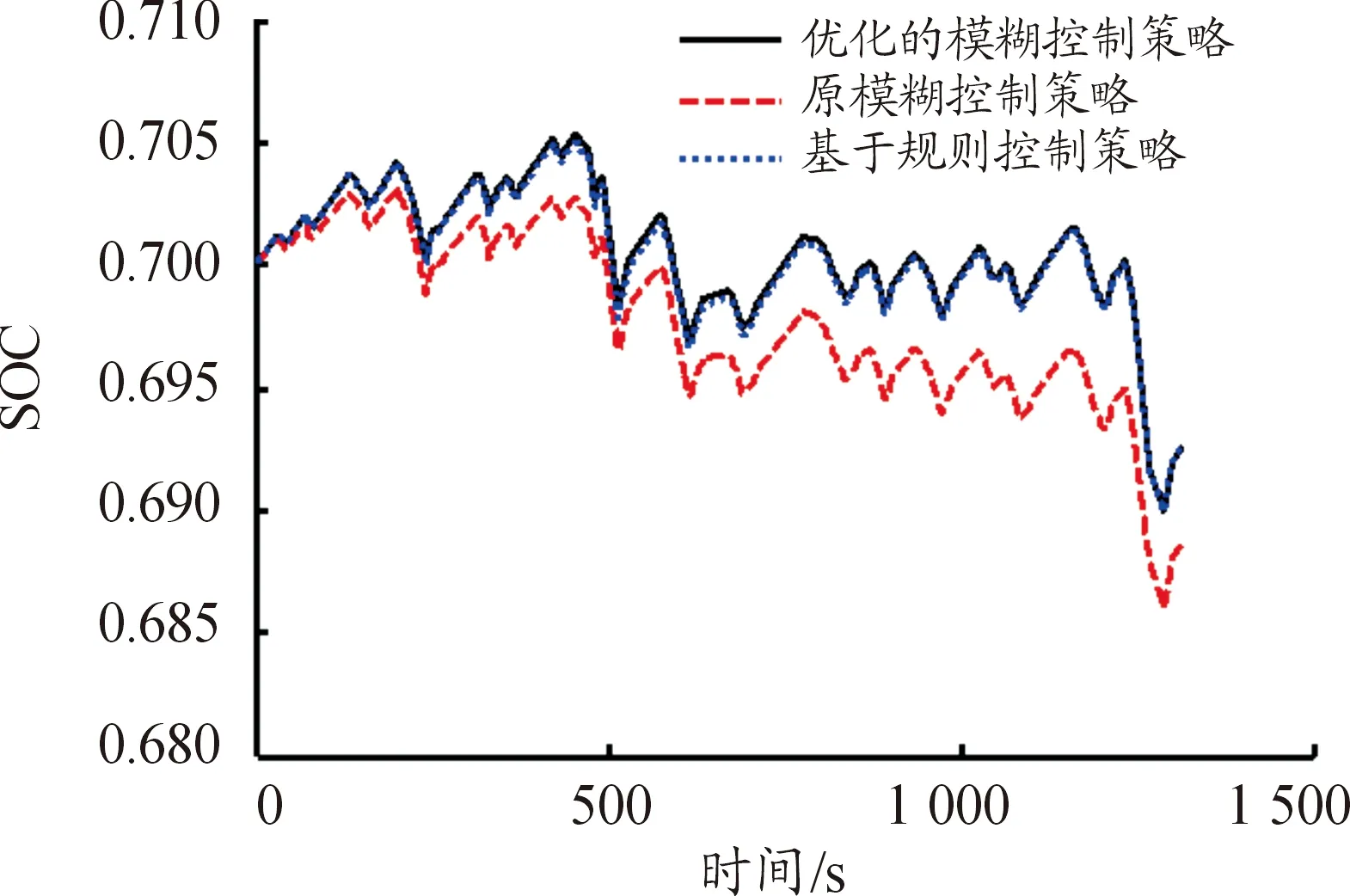
图12 SOC变化曲线

由图12可知，在初始值为0.7的前提下，3种能量管理策略均能保证SOC在合理范围内波动，但最终SOC的值也有显著差异，经过遗传算法优化的能量管理策略和基于规则式的能量管理策略SOC波动明显小于优化前的SOC波动，SOC变化率更小意味着动力电池单位时间内电量变化更小，更有利于动力电池的寿命。

3种能量管理策略对应的燃料电池输出功率变化如图13所示。

图13 燃料电池输出功率曲线

由图13可知，优化前的模糊控制策略会出现大幅度的燃料电池功率的波动，缩短燃料电池的寿命，而优化后的模糊控制策略和优化后的基于规则的能量管理策略均能保持较为稳定的状态，不会有剧烈波动，有助于延长燃料电池的使用寿命。

单工况下仅模拟客车行驶20 min，而实际行驶时间要远大于20 min。为更接近真实行驶状况，防止单工况下表现良好，而在延长工况下表现不良的情况，将单工况连续重复运行20次。仿真结果如图14所示。

图14 延长工况后SOC变化曲线

由图可知，基于规则的方法在SOC初始值为0.7时，20个工况后SOC已经可以稳定维持在0.68附近，表明该能量管理策略是可行和稳定的。经过遗传算法优化后的能量管理策略尽管在20个工况后SOC仍然下降，但将SOC起点改为0.5再进行仿真测试时，最终SOC仍会上升到0.6以上，将会在叠加更多工况后稳定维持在0.6以上，同样保证了动力电池在高效区域工作。

图15为电池初始SOC为0.7时各种能量管理策略下燃料电池的输出功率。由图可知，未经优化的模糊控制策略下，燃料电池输出功率会出现频繁的大幅抖动，不利于燃料电池的寿命。经过遗传算法优化后的能量管理策略和优化的基于规则的能量管理策略仍然表现稳定可靠。

图15 延长工况后燃料电池输出功率曲线

3种能量管理策略的等效能耗和燃料电池功率大幅变载次数如表3所示。由表3可知，经优化的模糊控制策略和基于规则的能量管理策略均比模糊控制能量管理策略表现更好，无论是在单工况还是多个重复工况下，整车经济性都得到了提升，且燃料电池输出功率大幅变载次数全部消失。当20个工况重复运行结束后客车共计行驶118.1 km，基于遗传算法优化的模糊控制策略等效能耗降低1.3%，基于规则的等效能耗降低0.8%，且SOC均在允许范围内波动，大幅变载工况均被避免。