效率最优的混合动力客车控制策略研究
2021-10-19谭伟,任萍
谭 伟,任 萍
(重庆理工大学 汽车零部件先进制造技术教育部重点实验室,重庆 400054)
混合动力汽车具有节能减排的显著特点,在动力性和续驶里程方面明显优于传统车辆和纯电动汽车。使用双行星排式动力耦合系统的混合动力车辆,输出动力通过两排行星机构将发动机输出功率分流成两部分传递,一部分通过机械路径传递至车轮,另一部分由电路径转化为机械能输出。由于两排行星机构具有分流汇流功能,可以使发动机与车轮处转矩和转速双重解耦,使发动机处于低油耗、高效率的工作区间,因此,车辆的燃油经济性较好。
由于双行星排式混合动力汽车在行驶过程中存在多种动力源耦合输入,在动力传动系统控制方面,需要综合考虑发动机和电机部件效率特性、耦合机构工作特性,因此,控制策略的设计变得非常复杂。针对行星排式混合动力汽车,许多研究学者进行了基于等效燃油消耗、模糊控制、线性二次规划、动态规划等优化算法的研究[1-4]。模糊控制具有非线性、鲁棒性和实时性等显著特点,在混合动力汽车控制中应用较多[5-8]。王伟等[9]针对双排行星式混合动力系统,以整车燃油经济性为目标,基于模糊智能控制提出发动机OOL控制策略;Leach S等[10]根据双模式电机复合无极传动系统功率分流特性建立功率损失模型,并进行仿真计算,但没有使用优化算法;王庆年等[11]对功率分流式混合动力系统提出基于瞬时效率最优的最佳分离因子算法,提升了其燃油经济性。综上,针对行星排式混合动力系统控制策略主要以发动机燃油消耗量为优化目标,国内外研究学者较少考虑到整个系统效率特性来设计能量管理策略。
本文从系统构型出发,基于杠杆理论建立动力耦合机构杠杆模型,分析得到不同动力源理论上的理想转矩分配特性,设计能量管理策略使发动机工作在机械点上或其附近,减少不同能量转化之间的损耗,并结合模糊智能控制,以达到在传动系统效率最优的基础上提升整车的燃油经济性的目的。
1 系统构型与整车参数
1.1 混合动力系统构型
图1表示采用行星轮系的混合动力耦合系统装置结构:该动力系统耦合装置由前排PG1和后排PG2两部分构成。发动机通过缓冲锁止机构与前排的行星架C1相连,后排齿圈R2固定在壳体上,齿圈R1与行星架C2相连,该构型实现了2个行星排的动力传递,最终动力经输出轴输出。

图1 动力耦合系统装置结构示意图
1.2 整车参数
表1为某款基于双行星排式的城市公交客车的整车主要技术参数。
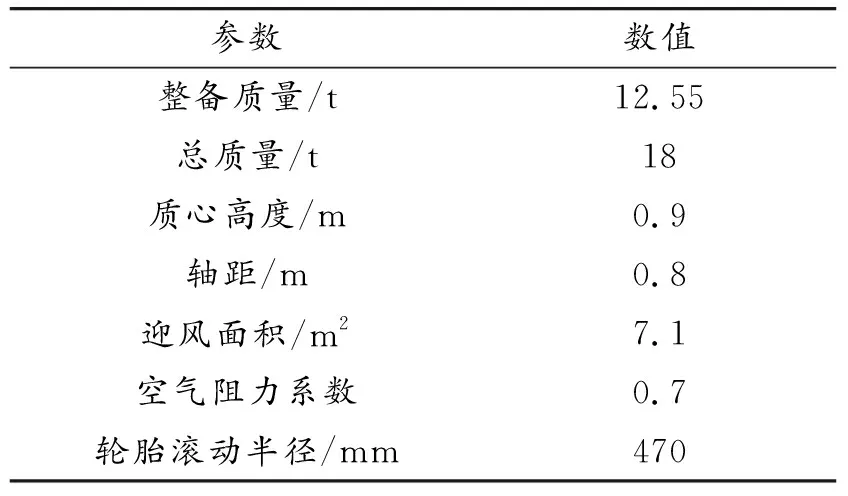
表1 整车主要技术参数
2 机械点分析
2.1 动力耦合机构杠杆模型
杠杆法可以通过简单、清晰的杠杆模型描述复杂的行星轮系,其基本原理为:将行星机构中各构件看成具有3个支点的垂直杠杆模型。垂直杠杆模型上的3个节点分别代表了混合动力耦合系统的太阳轮(S)、齿圈(R)及行星架(C),各节点的具体位置由行星排中的齿圈和太阳轮的齿数决定,各构件对应节点的水平位移及水平作用力表示相应的角速度和转矩,同时将行星轮系的旋转运动等效转化为直线运动,可以直观地对动力耦合机构工作特性进行分析,动力耦合机构垂直杠杆模型见图2。图示中K1与K2分别表示前后行星排的特征参数;ωR1、ωC1与ωS1分别表示前排各单一构件相应的转速,后排相应转速如上述表示;Tin表示前行星排齿圈和后行星排行星架相互作用的内力矩;TR2表示作用在后排齿圈上的外力矩;TC2则表示整车作用在动力耦合机构输出轴外力矩;TC1、TS1与TS2分别表示动力源作用在相应构件上的外力矩。
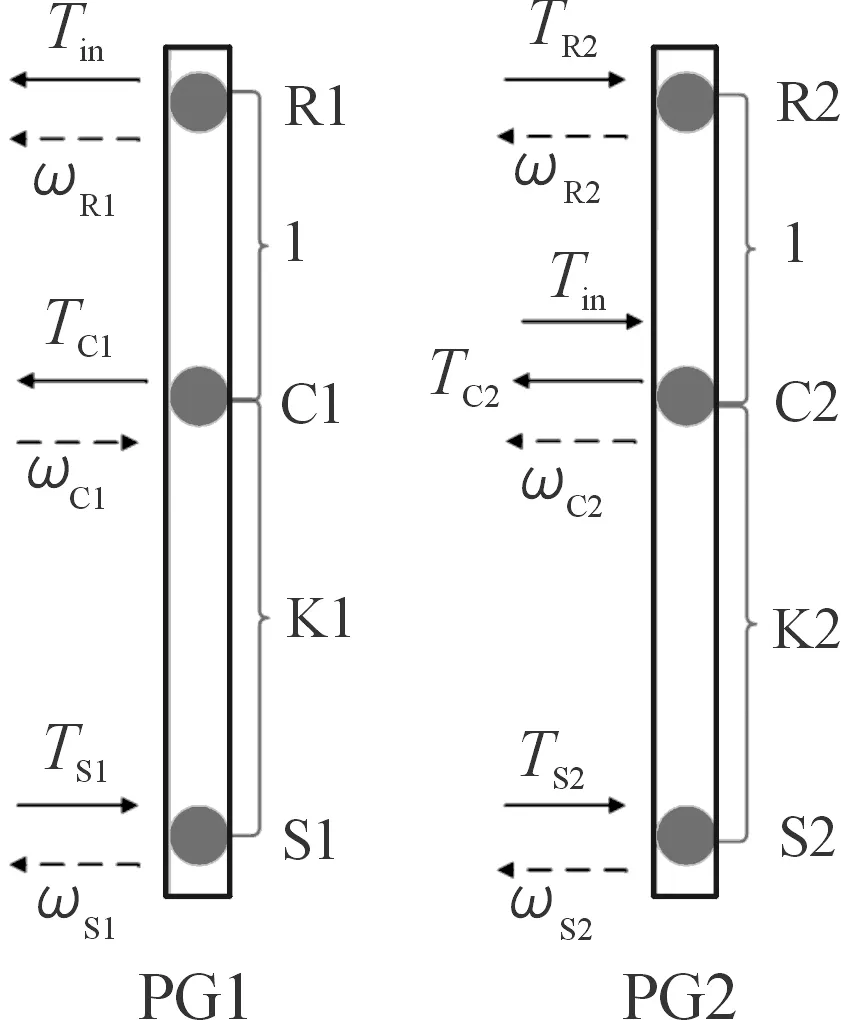
图2 动力耦合机构杠杆模型示意图
2.2 动力系统静态模型
为了准确分析动力耦合机构的工作特性和设计符合该模型的能量管理策略,建立动力耦合系统的数学模型。假设动力耦合系统各构件都为理想的无质量元件,且为刚性连接。
由上述的杠杆模型分析,针对前后行星排有:
TC1+TS1-Tin=0
(1)
TS1(1+K1)+TC1=0
(2)
TS2-TC2+TR2+Tin=0
(3)
TS2K2-TR2=0
(4)
其中,TS1和TS2又满足如下关系:
TS1=TMG1
(5)
TS2=TMG2
(6)
TC2=Tout
(7)
由上述动力耦合机构构型分析,可以得到前排PG1和PG2中各个构件的转速有如下关系:
(1+K1)ωC1=ωS1+K1ωR1
(8)
(1+K2)ωC2=ωS2+K2ωR2
(9)
从系统构型知发动机、MG1及MG2分别和前排行星架、前排太阳轮和后排太阳轮连接,故转速存在下述关系:
ωMG1=ωS1
(10)
ωMG2=ωS2
(11)
ωE=ωC1
(12)
由于该动力耦合系统后排齿圈固定,有:
ωR2=0
(13)
式中:TE、TMG1及TMG2分别表示发动机、电机MG1与电机MG2的转矩;ωE、ωMG1与ωMG2分别表示发动机、电机MG1和电机MG2的转速。
1) 当缓冲锁止机构处于锁止状态时,发动机不工作,结合上述公式,可以推导出MG1和MG2的转矩关系为:
(14)
2) 当缓冲锁止机构处于分离状态时,动力耦合系统各动力源的转矩分配有如下关系:
TC1=TE
(15)
(16)
(17)
以上建立了动力传动系统动力耦合机构的静态模型,得到不同动力源理论上的理想输出转矩。将其运用于整车能量管理策略的设计,为动力系统控制优化提供参考。
2.3 构型特性分析
对于本文中研究的双行星排式混合动力耦合系统,因为后行星排的齿圈被锁止,车辆在运行的状态中驱动电机MG2的转速不可以为0,因此,系统只存在1个机械点i,其具体值表示为:
(18)
该混合动力耦合系统输入与输出的转速比值为:
(19)
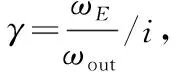
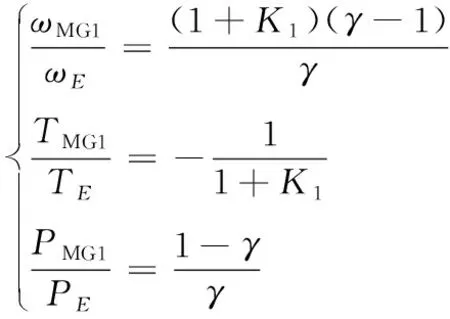
(20)
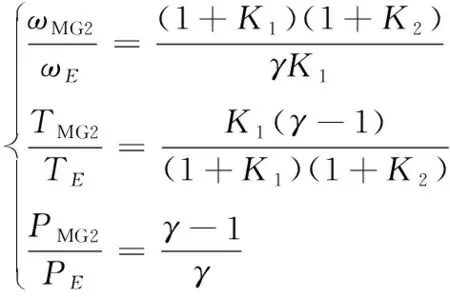
(21)
3 控制策略设计
3.1 动力系统工作模式
通过对上述混合动力耦合系统构型分析可知,混合动力耦合系统能实现串联和并联状态的相互切换,通过合理控制多个动力源的工作状态,让动力传动系统在以下4种工作模式之间切换,如表2所示。

表2 动力系统工作模式
通过以上对动力耦合机构的不同动力源工作状态的控制,该动力耦合系统可实现以下工作模式:
1) 纯电动模式:当车速和整车需求功率均较低,同时电池SOC满足纯电动驱动条件时,混合动力系统处在纯电动模式状态。
2) 混合驱动模式:当动力电池SOC不足且整车需求功率较高时,发动机启动并处于工作状态,此时使发动机工作在最优工作曲线上,其余功率由电机补充提供。
3) 制动能量回收模式:当车辆减速行驶时,通过电机产生力矩对车辆进行制动,同时进行制动能量回收。
4) 停车充电模式:当动力电池SOC较低,在车辆停车期间,让电机工作在发电模式,此时通过电机给动力电池充电。
3.2 基于效率最优的机械点控制策略
由上述的动力耦合系统可知,基于双行星排式的混合动力汽车的燃油经济性不仅取决于单一部件的效率,还需要考虑整车的系统损耗[12-13]。为了提升车辆的整车燃油经济性,需要考虑动力耦合机构双行星排工作特性,若电路径功率值为零时,混合动力系统输出功率全部为发动机经过机械路径提供,系统的传动效率达到最高点,对应的传动比即系统的机械点。
为了更好地降低油耗,将动力耦合机构各部件特性综合考虑,通过调节系统传动比,减少系统的功率循环,从而保证传动系统的效率较高,达到提升整车燃油性的目的[14]。根据上述建立的动力耦合机构静态模型,在混合驱动模式中,机械点控制策略通过调节系统传动比R使电机对发动机转速进行协调控制,设定阈值K,让发动机能够在机械点或者附近运行,从而确保系统传动效率较高[15-16]。
3.3 模糊控制策略
为了实现动力耦合系统不同动力源最佳功率分配、降低油耗且兼顾动力电池SOC,同时解决上述机械点控制策略下发动机低效率问题,设计了模糊控制器[17-20]。当发动机参与工作时,给定输入变量SOC与油门踏板开度,将2个输入变量进行模糊化处理,然后根据制定的模糊控制规则优化决策,最终将优化的发动机需求功率输出。本文中设计的模糊控制工作原理如图3所示。

图3 模糊控制工作原理示意图
模糊智能控制策略属于智能控制算法范畴,核心为模糊控制器,且由规则库、推理机制、模糊化接口和去模糊化接口四部分构成。这里的模糊控制策略在Matlab/Simulink中完成设计,其中隶属度函数的设计为模糊控制器的基础,隶属度函数的形状直接影响系统灵敏度和系统控制特性。动力电池SOC的模糊集合为{XS,S,M,B,XL},分别代表极低、低、中、高、极高;油门踏板开度的模糊集合为{VS,S,M,B,VB},分别代表极小、小、中、大、极大;发动机需求功率的模糊集合为{SS,S,M,B,BB},分别代表极小、小、中、大、极大。本文中设计的模糊控制器输入及输出的论域与隶属度函数如图4所示。
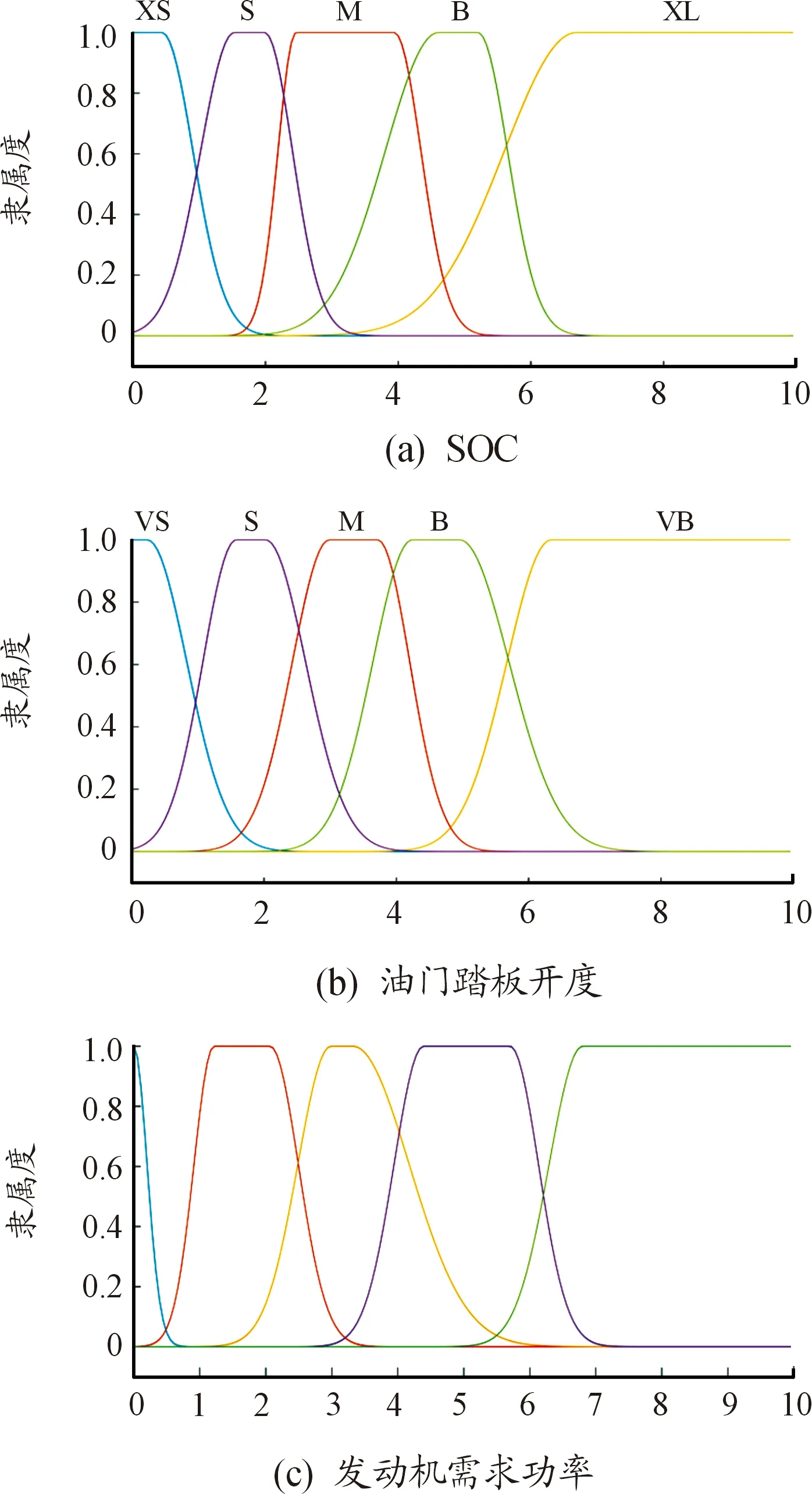
图4 模糊控制器输入、输出变量隶属度函数
模糊控制规则依据规律如下:
1) 当动力电池SOC较高时,如果整车需求扭矩大于发动机最大扭矩,则使发动机工作在最优曲线周围,余下转矩则由电机补充;当车辆需求转矩较小时,则控制发动机运行在经济工作区间,剩余转矩由电机补充。
2) 当动力电池SOC较低时,如果整车需求扭矩小,在满足整车动力性的基础上,使发动机运行在经济区间,同时多余的能量为电池充电;如果需求转矩大,则发动机提供最大扭矩,余下扭矩则为电池充电。
3) 当动力电池SOC处于上述两个中间状态时且车辆需求转矩不高,此时使用上述设计的机械点控制策略。
制定的模糊规则采用“IF-THEN”推理规则,具体见图5。
图5 模糊控制规则曲面
4 仿真与结果分析
为了验证所提出的机械点控制策略和模糊控制策略结合具有合理性和优越性,在AVL/Cruise搭建整车仿真模型,Matlab/Simulink搭建整车控制策略,使用DLL接口进行联合仿真。搭建的整车模型和控制策略原理见图6、7。
图6 整车模型示意图
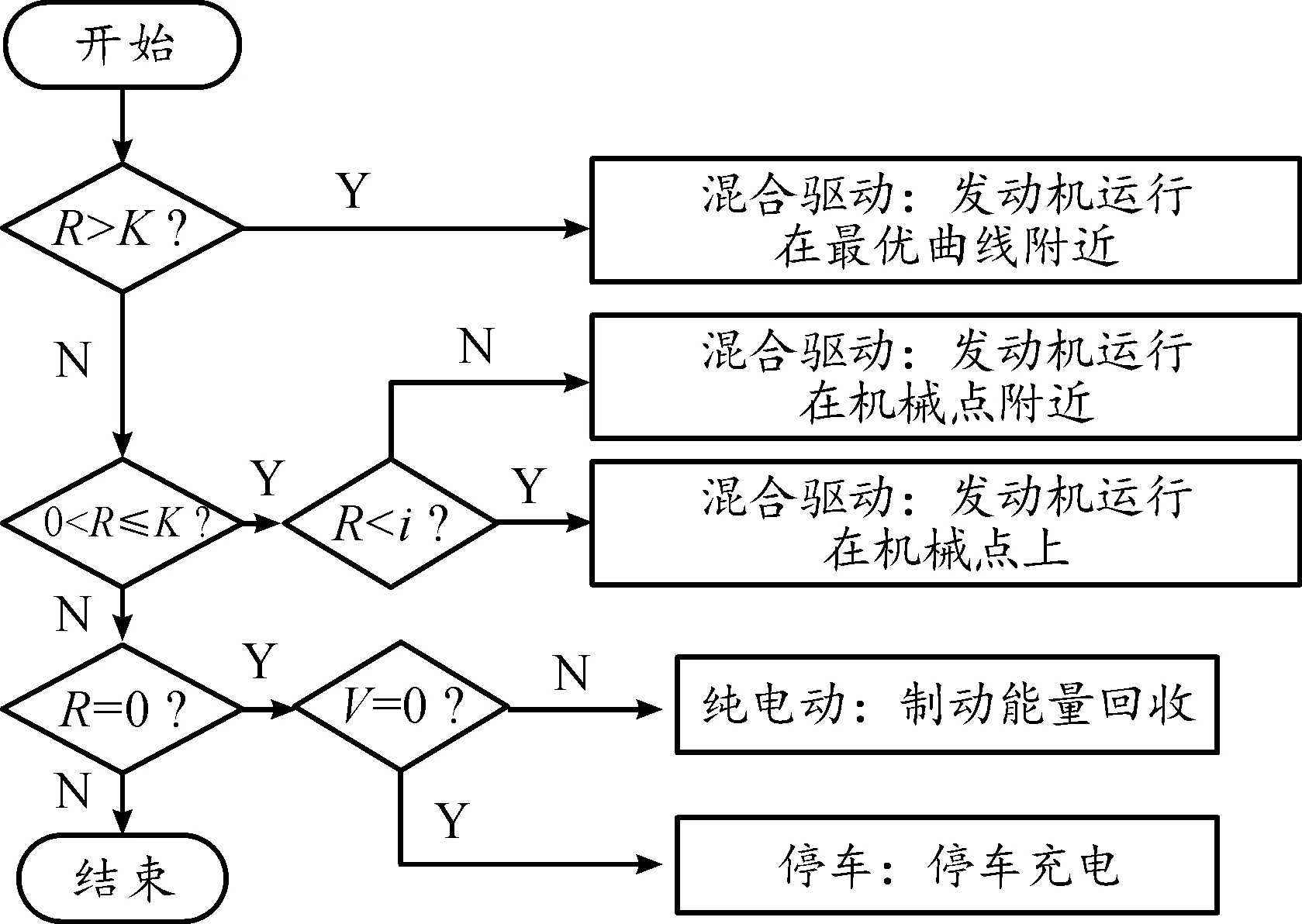
图7 控制策略原理框图
选用中国典型城市公交循环工况进行车速跟踪及仿真测试,该循环工况具体信息见表3。

表3 CBCC循环工况
图8为搭建的模型在中国典型城市公交循环工况下车速跟随仿真验证测试结果。从图8中可以看出,循环工况目标车速与实际车速2条曲线基本吻合,结果表明建立的模型能较好地跟随循环工况车速的变化。
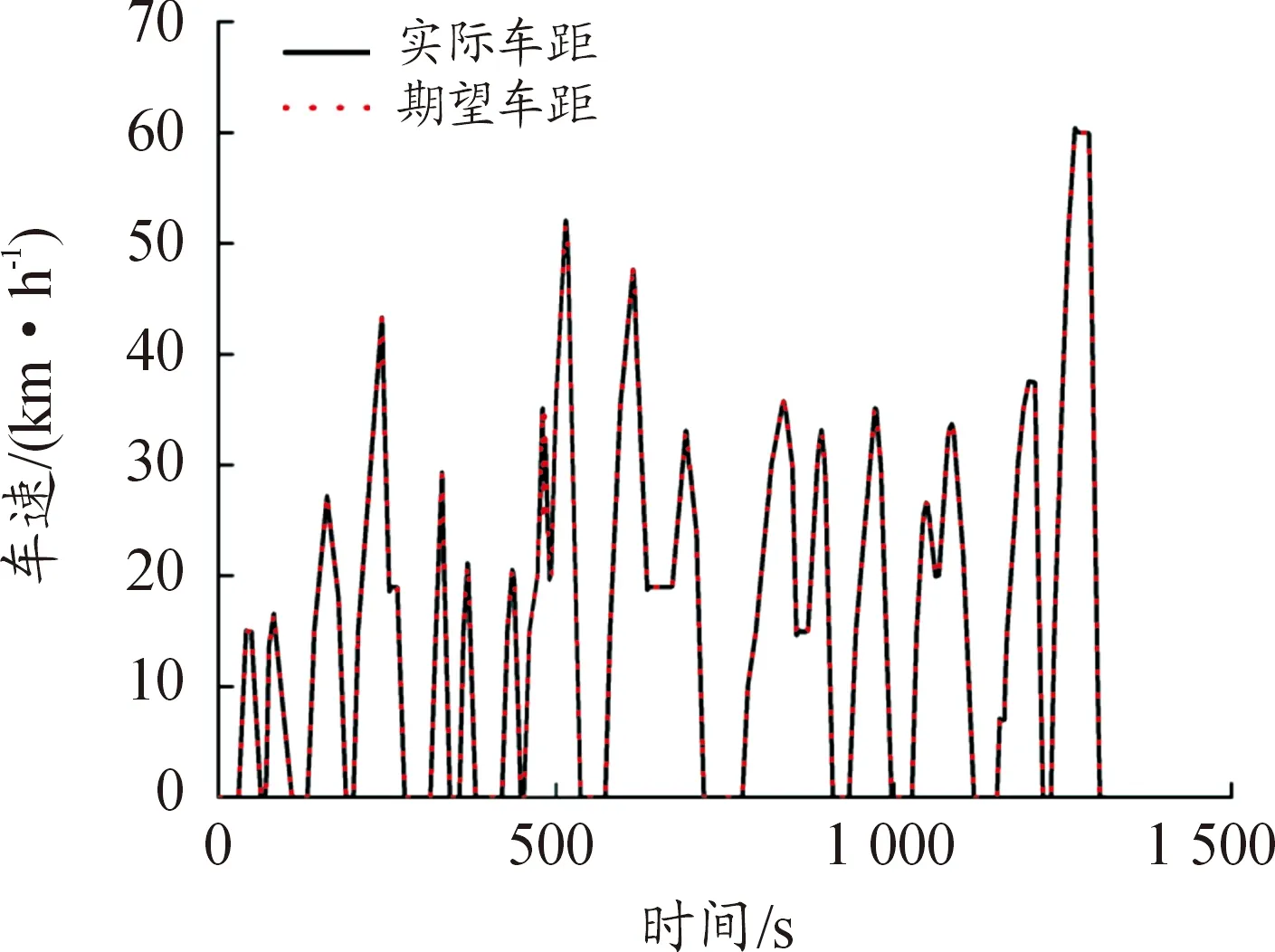
图8 车速跟随曲线
图9显示了动力电池SOC变化情况。分析可知,SOC在整个循环工况发生较小范围波动,且其值保持在50%以上,实现了动力电池SOC动态均衡,表明车辆在整个行驶过程中,动力电池不仅向车辆提供动能,还在整车需求功率较低时将多余的能量储存起来,达到电池的设计要求。
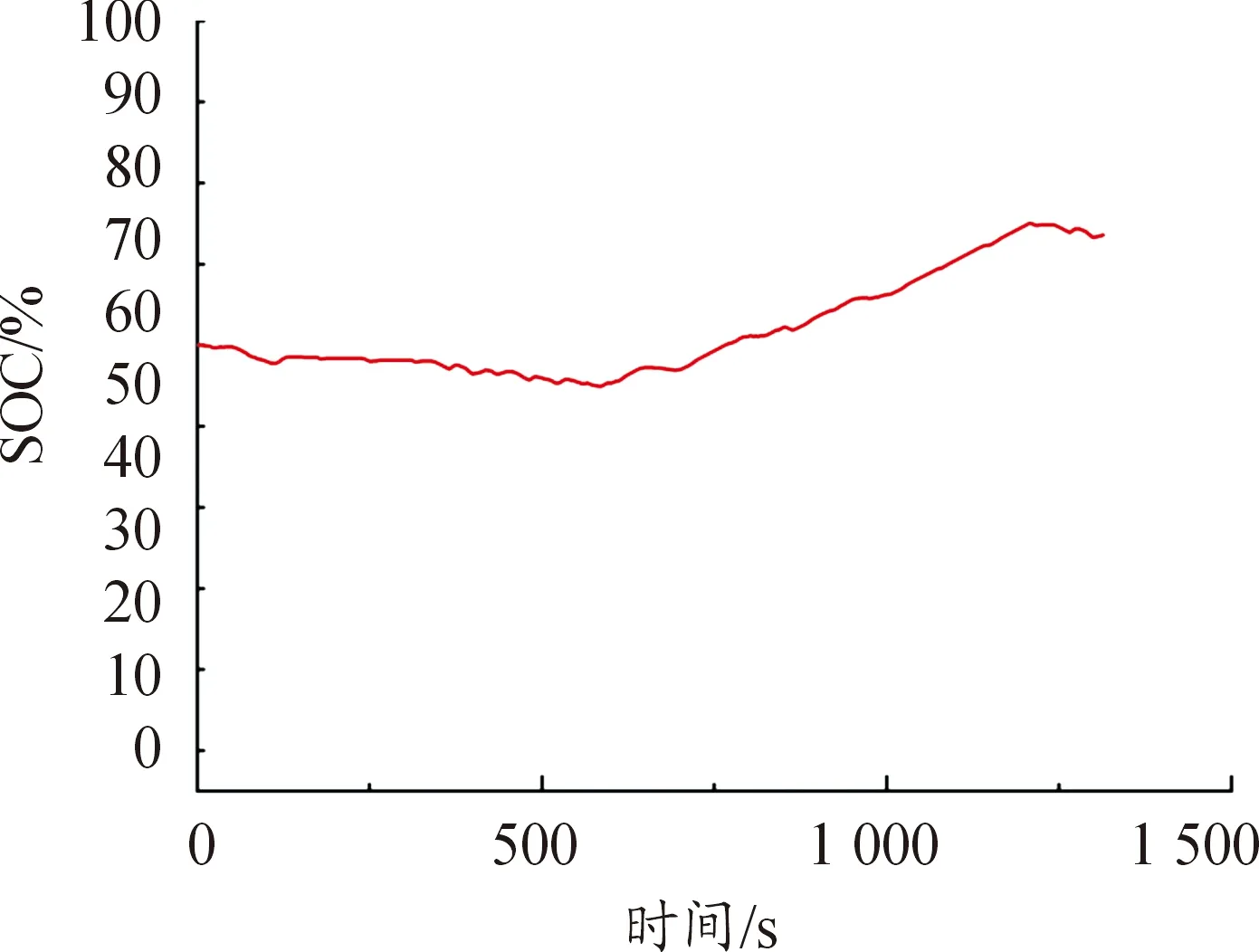
图9 SOC变化曲线
图10、11表示联合仿真结果所得到的动力耦合系统2个电机的扭矩图,图12为发动机输出功率曲线。可以看出,混合动力系统在纯电动模式下运行时间占比较多,这时驱动电机MG2驱动车辆运行;当系统为停车充电模式时,发动机带动电机MG1给动力电池充电,让动力电池SOC稳定维持在给定范围内;当系统工作在混合驱动模式时,发动机和2个电机均处于工作状态,此时MG1与MG2提供动力辅助发动机驱动车辆。
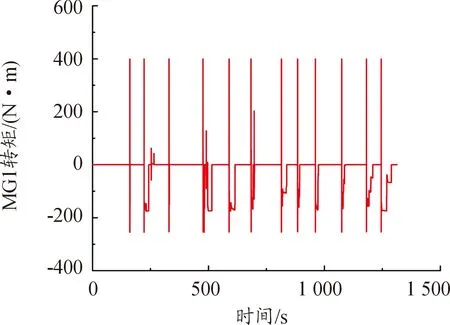
图10 电机MG1扭矩曲线
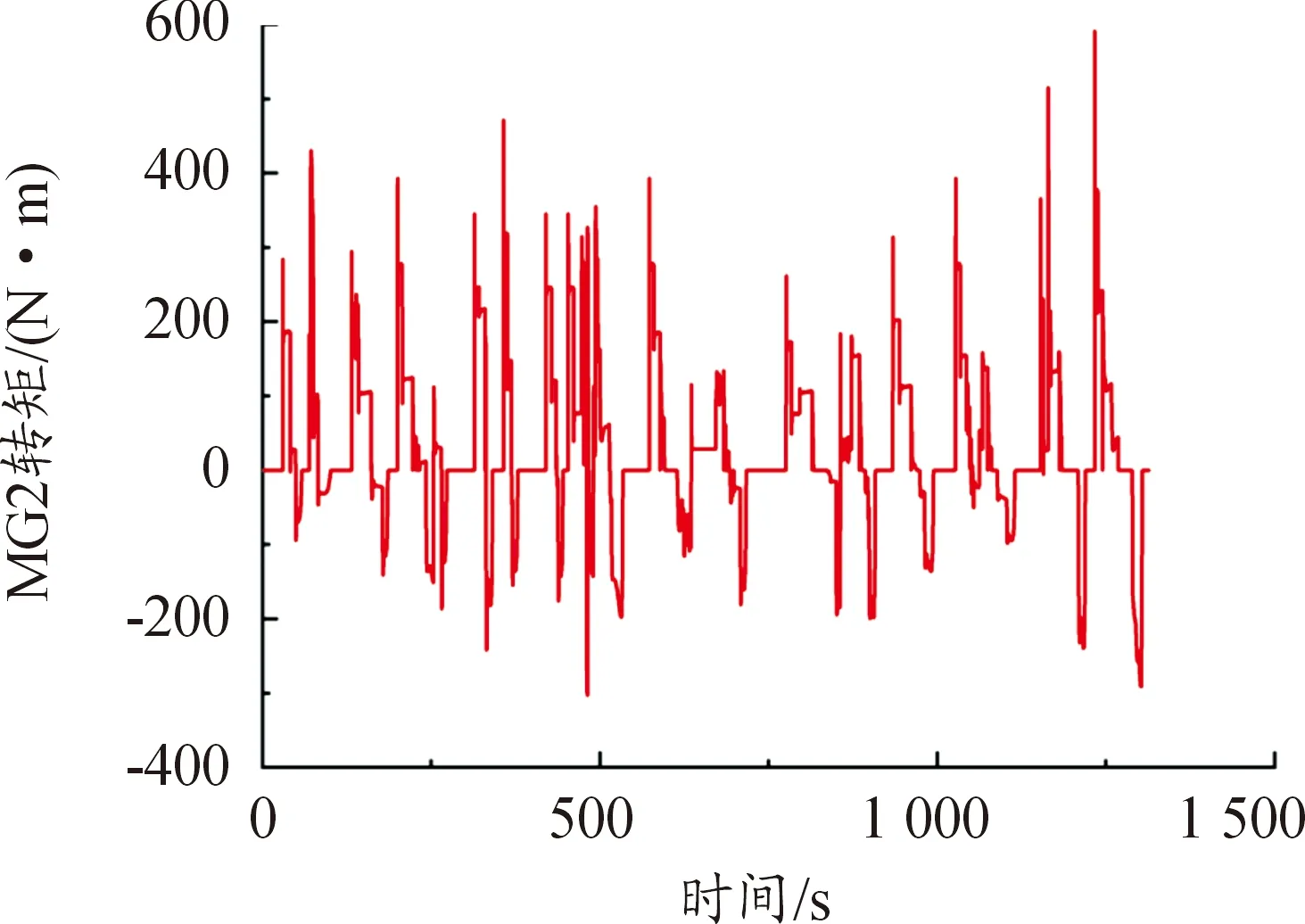
图11 电机MG2扭矩曲线
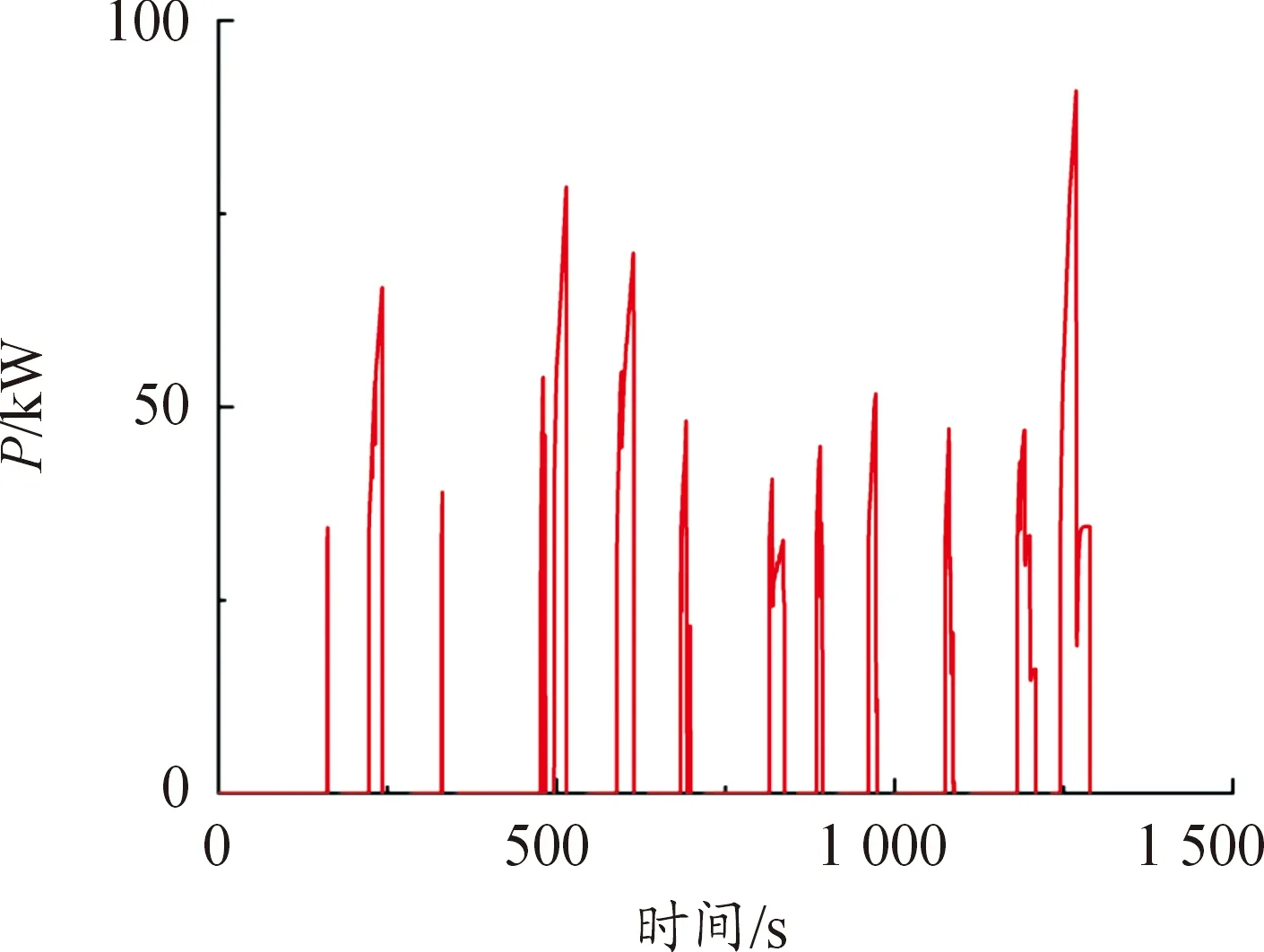
图12 发动机的功率曲线
图13为发动机工作点的分布情况,发动机工作在图中标注的两点。可以看出,发动机工作点在低油耗区域,符合设计的控制策略思想,达到了提高燃油经济性的目的。

图13 发动机工作点分布情况示意图
基于提出的控制策略,在中国典型城市公交循环工况测试下,动力性方面,最高车速可以达到90 km/h,大于法规规定的公交车最高车速69 km/h。在燃油经济性方面,百公里油耗为20.29 L,与该动力耦合系统应用于城市公交车的试验结果相比,燃油经济性提升了23.4%。
考虑到所提出的功率分配策略在不同循环工况下的通用性与适用性,仿真选用FTP75、NEDC市区工况及UDDS工况组合进行研究。工况信息和仿真车速跟随结果如图14所示。
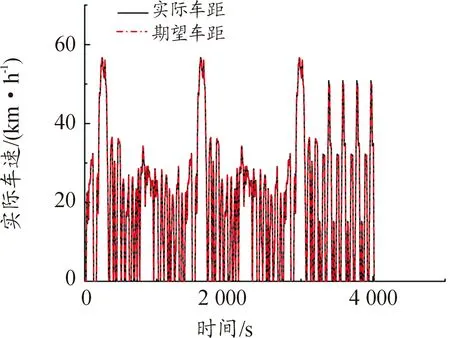
图14 混合工况车速跟随曲线
在混合工况仿真测试下,图15、16为驱动电机和发动机的仿真结果。表4给出了不同工况下的燃油经济性,分析可知,动力耦合系统的功率分配合理,验证了控制策略的优化控制效果。
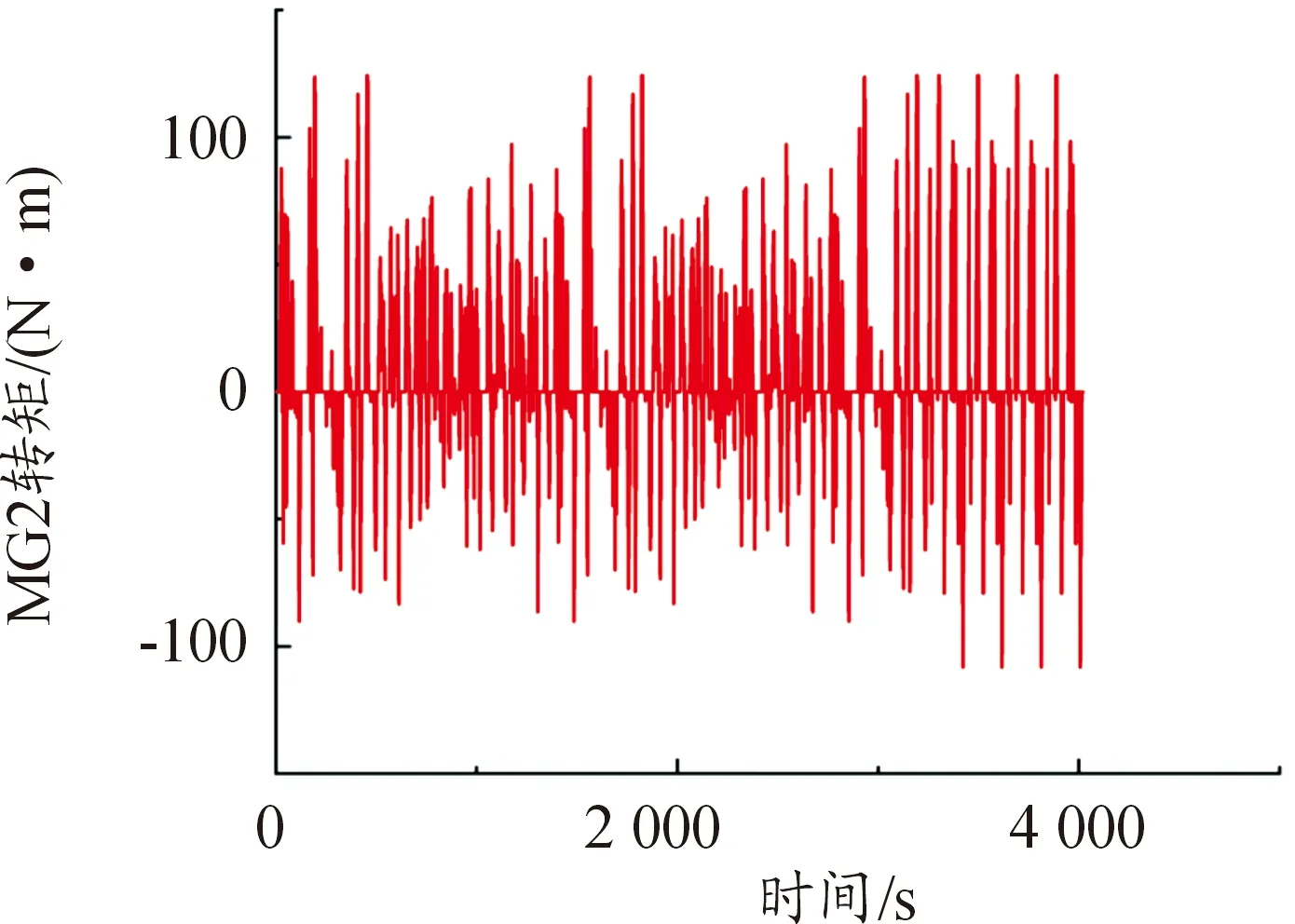
图15 电机MG2扭矩曲线
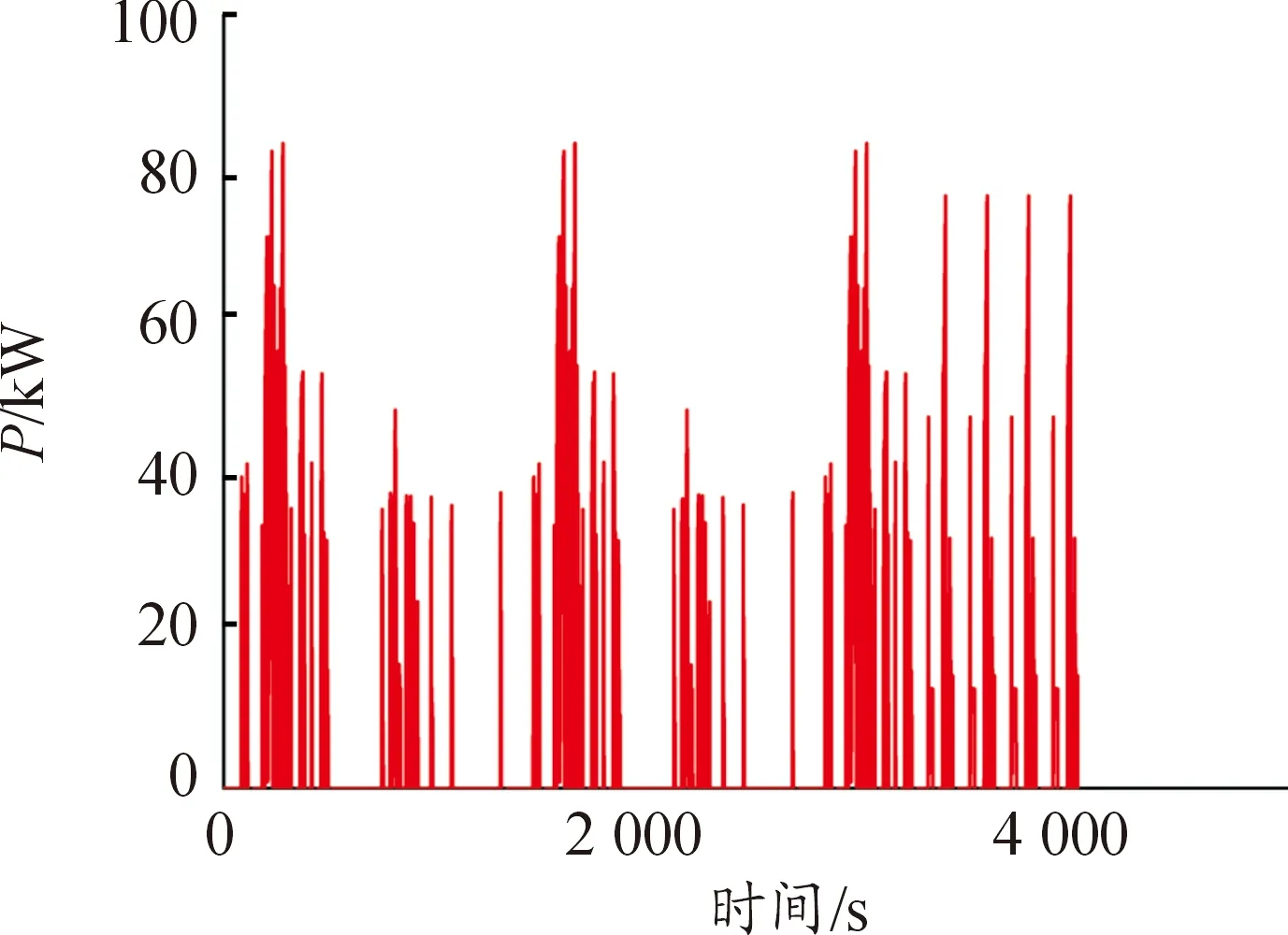
图16 发动机的功率曲线
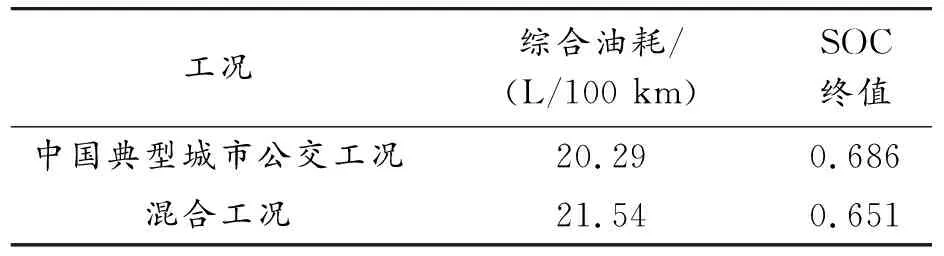
表4 不同工况的燃油经济性
5 结论
基于某双行星排式混合动力客车,针对动力耦合系统不同部件工作特性,基于杠杆法建立动力耦合机构静态模型,为减少功率循环,保证动力传动系统较高效率,提出了机械点控制策略,同时结合模糊智能控制对整车能量管理策略进行优化控制。在Matlab/Simulink中设计整车能量管理策略,模式切换在Stateflow中搭建,整车模型在CRUISE中搭建,在中国典型城市公交循环工况下进行仿真验证。结果表明:所搭建的整车仿真模型能够较好地跟踪循环工况车速变化,达到整车的设计需求,能够使动力电池SOC在理想范围内波动,实现了发动机与2个电机的协调工作,发动机工作点落在经济区间,且降低了整车油耗,验证了所提出的控制策略对混合动力系统能够实现较好的控制。以上分析结果对双行星排式混合动力客车的动力系统控制策略研究有参考意义。
