基于设计地震动的斜入射波时程确定方法对土石坝地震响应的影响

王 飞, 宋志强, 刘云贺, 张剑峰

(1.西安理工大学 省部共建西北旱区生态水利国家重点实验室,西安 710048； 2.中国三峡建设管理有限公司,成都 610041)

地震动输入是大坝抗震设计计算的前提，入射波是地震动输入的基础。GB 51247—2018 《水工建筑物抗震设计标准》[1]规定采用平坦基岩地表水平向地震动峰值加速度作为表征设计地震动强度的主要参数，设计地震动是抗震计算的依据，因此，研究设计地震动下入射波幅值及时程确定方法具有重要实际工程意义。在进行大坝抗震设计计算时，通常假定地震波垂直入射[2]，按一维反演方法依据坝址设计地震动水平分量确定入射波幅值和时程。然而，当工程场地距震源较近时，地震波经过有限次反射和透射后到达地表，并不满足垂直入射假定[3-5]。因此，有必要研究地震波斜入射时基于水平和竖直两向设计地震动的入射波幅值和时程确定方法。

进行地震波斜入射下结构地震响应分析时，很难确定地基底部地震波时间序列，通常仍然按照垂直入射的方法，直接把实测地震动记录或者人工合成地震动水平分量当作入射波，再或者进行1/2倍调幅，把调幅后的地震动作为入射地震波。张树茂等[6]将场地谱地震动时程作为地基底部入射波，研究了P波和SV波斜入射下土石坝加速度反应随入射角的变化规律。王飞等[7]以实测近断层地震动记录作为基岩地基底部的斜入射波，研究了近断层地震动斜输入作用下水电站厂房的非线性地震响应。孙纬宇等[8]以EI-Centro波、Northridge波和宁河波作为入射波，研究了P波和SV波斜入射下河谷场地地震动放大系数随入射角的分布特征。Sun等[9]和李明超等[10]将平坦基岩地表水平向设计地震动按1/2倍调幅，以调幅后的地震动作为基岩地基底部的入射波，分别研究了地下水工隧洞和重力坝的非线性地震响应随地震波入射角度的变化规律。单纯分析地震波斜入射下结构的地震响应时，上述入射波时程确定方法是能够接受的，但上述方法在任意角度下入射波幅值和时程是不变的，没有考虑斜入射波时程与入射角度的内在联系，造成地表水平地震动峰值随入射角变化而变化[11]，获得的结构地震响应随入射角变化的规律包含了地震动强度变化的贡献，导致结构的地震响应并不是设计地震动作用下的结果。

本文在P波和SV波组合斜入射前提下，考虑两者对半无限空间自由场的共同贡献，基于波场叠加原理，构建了均质基岩二维空间自由场，根据控制点自由场运动分量与设计地震动对应分量相同的原则，建立入射波时程与入射角度的函数关系，提出了基于设计地震动的入射波时程确定方法。分析了按垂直入射假定确定斜入射波时程时半无限空间地表自由场和基岩-覆盖层-土石坝系统地震响应相对于本文方法的偏差。应用本文方法分析了斜入射引起的地表非一致运动，研究了相同设计地震动条件下，不同斜入射角对土石坝的非一致地震响应影响规律。

1 基于设计地震动的斜入射波时程确定方法

1.1 方法1

通常情况下，基岩平坦地表地震动假定由垂直地表的入射波和同相位等幅值的反射波叠加组成，该假定对于距震源较远场地上的地震动是合理的，此时，基岩地基底部入射波可按平坦自由地表水平向设计地震动1/2调幅获得，称为方法1。

当P波或SV波入射角为0°时，平坦地表自由场地震动幅值和波形与设计地震动吻合。但当震源距离坝址较近时，入射波传播方向与水平地表并非垂直，而是与水平地表的法向存在不确定性夹角。当研究基于设计地震动的斜入射地震波对结构地震响应的影响时，仍按方法1确定斜入射波时程，由于不考虑斜入射波时程随入射角度的变化而变化，因此随着入射角增大，平坦地表地震动幅值和波形将逐渐偏离设计地震动：根据王飞[12]的研究结论，当平面P波斜入射时，平坦地表水平向地震动强度随入射角增大先增大后减小，竖向地震动强度随入射角增大而减小；当平面SV波斜入射时，水平向地震动强度随入射角增大而增大，竖向地震动强度随入射角增大先增大后减小。

1.2 方法2

近地表入射地震波成分复杂，基岩平坦地表设计地震动不能假定仅由某一类型体波组成。而应该考虑两种体波的共同作用。平面P波和SV波斜入射至自由地表均会产生反射P波和SV波，如图1所示。虚线箭头表示地震波的传播方向，实线箭头表示质点振动方向。坐标原点O为控制点，设计地震动水平分量为ux(t)，竖向分量为uy(t)。入射P波位移波函数为g(t)，振动矢量m(0)=(sinα, cosα)，入射SV波位移波函数为f(t)，振动矢量n(0)=(cosγ,-sinγ)。半无限均质弹性空间任意点自由场由两种体波(P波和SV波)的入射波场、反射波场共同叠加组成[13]

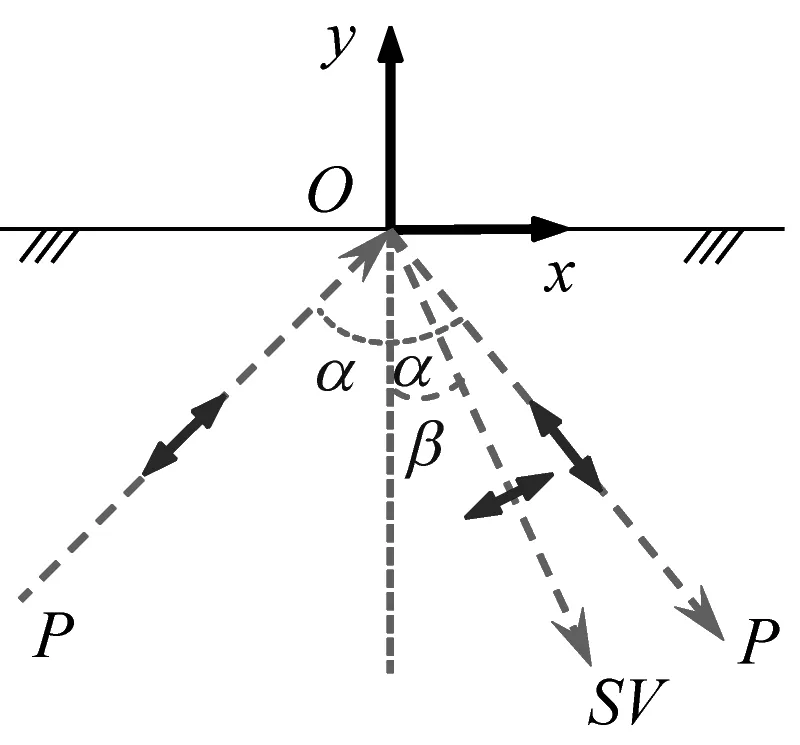
(a) P波斜入射

水平向

(1)

竖向

(2)

式中：cP和cS分别为P波和SV波波速；A1，A2为P波斜入射下反射P波和反射SV波幅值与入射P波幅值的比值;B1,B2为SV波斜入射下反射SV波和反射P波幅值与入射SV波幅值的比值，分别如下

(5)

式中,E,ρ和μ分别为介质的弹性模量、密度和泊松比。

在水平自由地表，y为一常数且等于零，结合Snell定律，水平自由地表任意点自由场可表示为

水平向

(7)

假设水平自由地表任意点的运动在整个时间历程中由入射P波和SV波共同作用，即P波和SV波同时传播至水平自由地表，则有式(8)成立

(8)

取任意点为控制点O(x=0,y=0)，则需要满足的条件是该点的自由场水平向和竖向分量与设计地震动对应的两向分量相同，根据式(6)和式(7)，可得到两个方程

水平向

ag(t)+bf(t)=ux(t)

(9)

竖向

cg(t)-df(t)=uy(t)

(10)

式中:a=(sinα+A1sinα-A2cosβ);b=(cosγ-B1cosγ+B2sinθ);c=(cosα-A1cosα-A2sinβ);d=(sinγ-B1sinγ-B2cosθ)。当设计地震动两分量和半无限空间介质信息已知时，联立式(9)和式(10)，可以建立P波和SV波时程关于入射角的函数关系式，进而可由入射角推求组合入射波时程。为方便起见，将本文建立的考虑斜入射P波和SV波对设计地震动的组合贡献、根据入射角度确定入射波时程的方法称为方法2。

2 不同斜入射波时程确定方法对均质半无限空间自由场响应的影响

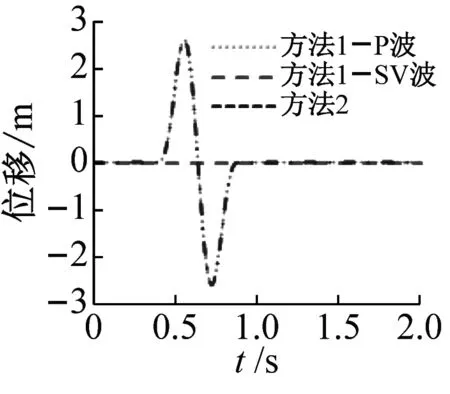
从平面半无限均质空间截取长度为400 m(2L)、深度为200 m(H)的有限域地基，如图2所示。地基弹性模量为1.3 GPa，密度为2 000 kg/m3，泊松比为0.25。P波波速为883 m/s，SV波波速为510 m/s。地表控制点O设计地震动水平和竖向位移时程均如式(11)所示，位移波形如图3所示。位移峰值为2.60 m。基于设计地震动时程，按照方法1确定P波或SV波单波斜入射时程，按照方法2确定与入射角度相关的P波和SV波组合斜入射时程。假定单波或组合波均从地基左侧斜向上入射，分析不同斜入射波时程确定方法对O点自由场响应的影响。

图2 半无限均质弹性空间计算模型(m)

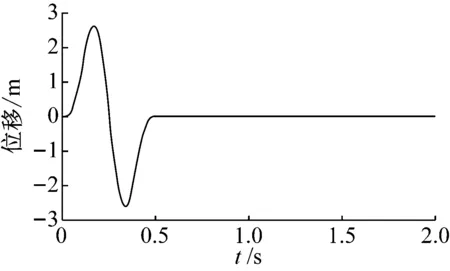
图3 水平向和竖向设计地震动时程

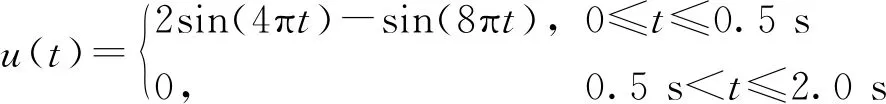
(11)

方法1和方法2均是先给定P波斜入射角，然后按照式(8)确定SV波斜入射角，表1给出了不同入射角度下入射波位移峰值、地表O点水平和竖向位移峰值及其相对设计地震动峰值的误差。表1表明，方法1任意入射角度下，入射P波或SV波位移峰值均是设计地震动水平向峰值的1/2，即为1.30 m。方法2中入射P波位移峰值随入射角度增大而增大，入射SV波位移峰值随入射角增大而减小。不管何种入射角下，方法2中O点水平和竖向位移峰值均与设计地震动吻合，而在相同入射角下，方法1获得的地表O点自由场响应与设计地震动差异显著：其中当P波入射角为45°时，O点水平向和竖向位移峰值分别比设计地震动减小了23.85%和31.63%，当SV波入射角为24.1°时，O点水平向和竖向位移峰值分别比设计地震动减小了2.31%和62.69%。

表1 不同入射波时程确定方法下O点位移峰值及其相对设计地震动误差

图4和图5分别给出了不同入射角下地表O点水平向和竖向位移时程曲线，由图4和图5可知:方法2中P波、SV波组合入射前提下，不论何种入射角度组合，地表点O水平向和竖向位移波形与设计地震动完全吻合，该斜入射波时程确定方法能够反映设计地震动作用下半无限空间自由场响应。方法1中，当P波斜入射或者SV波斜入射时，点O位移波形均与设计地震动有较大差异。

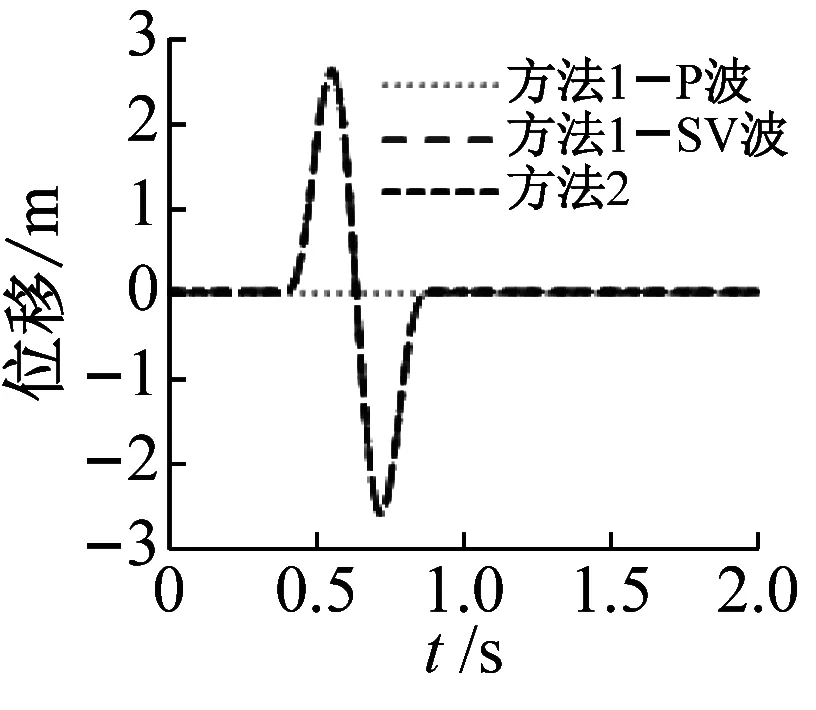
(a) P波0°，SV波0°

(a) P波0°，SV波0°

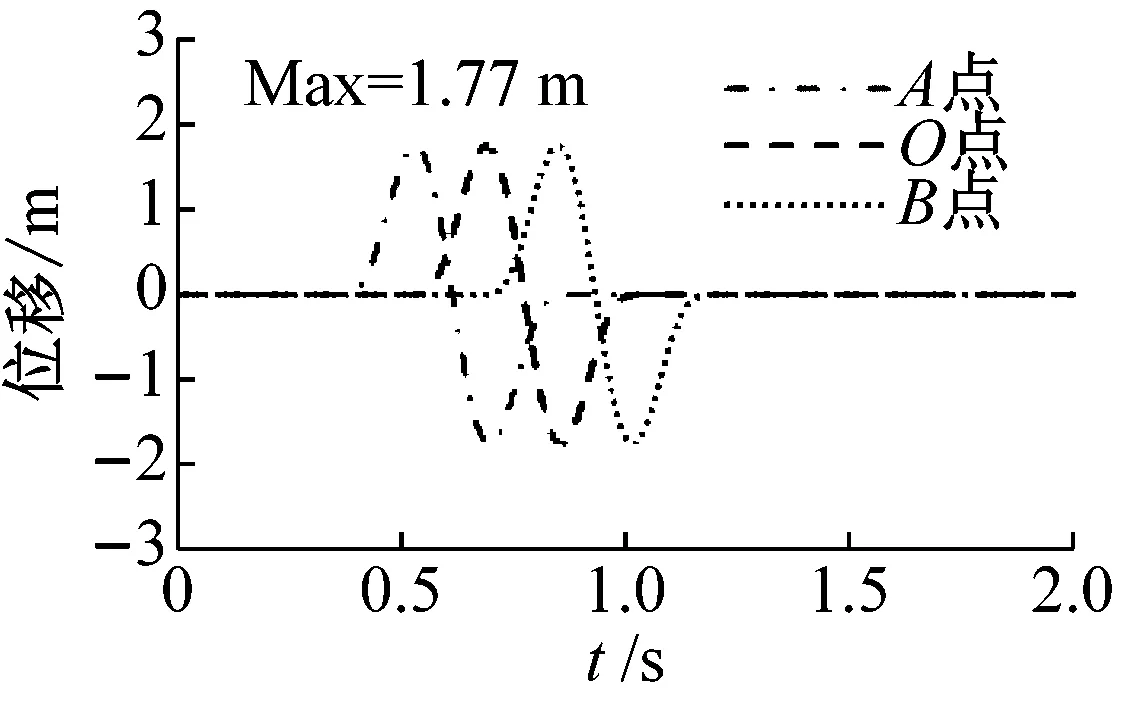
图6和图7分别给出了两种方法获得的P波入射角为45°、SV波入射角为24.1°时地表O点和左上角A点、右上角B点的水平向和竖向位移时程曲线。由图6和图7可知:地震波斜入射引起地表空间点发生非一致运动，任意两点开始振动的时间间隔随入射角的增大而增大。方法1表现的非一致运动峰值与设计地震动峰值有较大的误差，方法2表现的非一致运动波形和峰值均与设计地震动吻合，方法2能够反映设计地震动下的地表非一致运动。

(a) 方法1中P波斜入射

(a) 方法1中P波斜入射

当斜入射波幅值取设计地震动幅值的1/2且只包含一种体波(P波、SV波)时，地表自由场运动与设计地震动误差较大，难以反映设计地震动下的斜入射波作用下结构的地震响应。考虑P波和SV波对半无限空间自由场的共同作用，按入射角确定入射P波和SV波时程，获得的地表自由场运动与设计地震动吻合，并且各点地震动呈现出明显的非一致性，能够合理反映设计地震动下的斜入射波作用下结构的非一致地震响应。

3 不同斜入射波时程确定方法对土石坝地震响应影响

3.1 计算模型

以坐落在覆盖层地基上的均质土石坝为研究对象，坝高100 m，坝顶宽10 m，上游、下游坝坡均为1∶1.6，覆盖层深度为100 m，基岩地基底部取至地表以下200 m处，基岩-覆盖层-土石坝系统，如图8所示。采用邓肯-张E-B模型[14]描述坝料和覆盖层的静力非线性弹性行为。动力时程计算采用等效线性方法，坝料和覆盖层土体采用沈珠江等[15]建议的修正等效黏弹性模型，动力计算参数,如表2所示。表2中k1，k2和n均为土石料动三轴试验参数，λmax为最大阻尼比，μ为泊松比。基岩弹性模量、密度和泊松比分别为8 GPa，2 750 kg/m3和0.24。

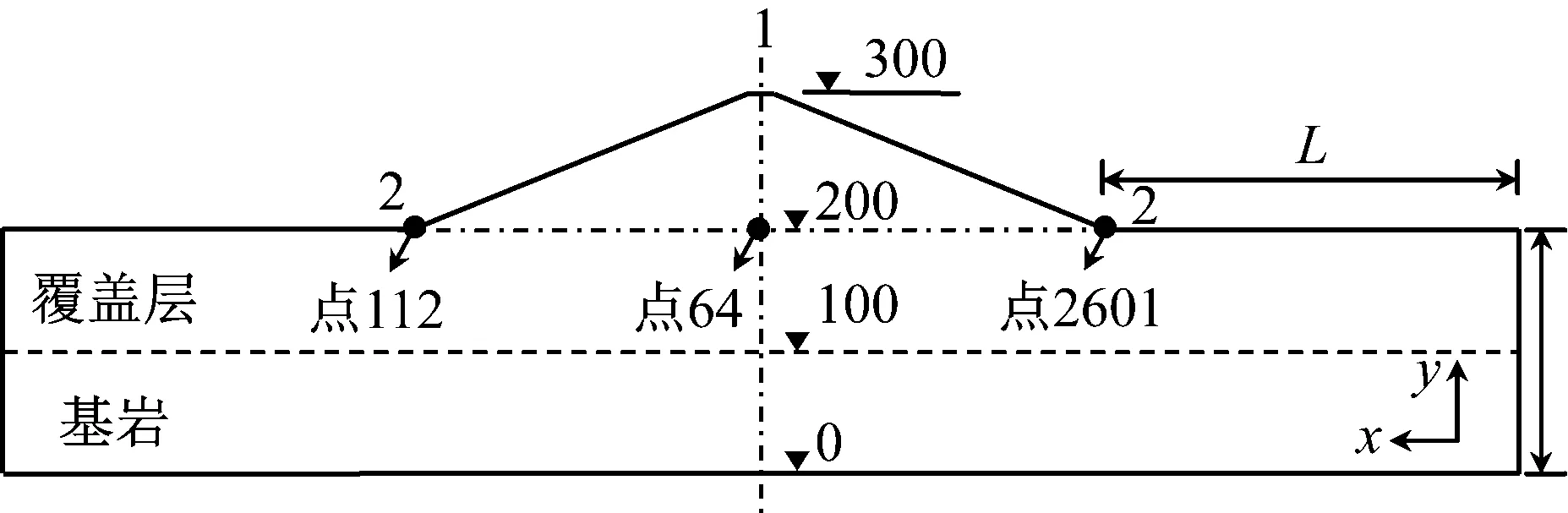
图8 基岩-覆盖层-土石坝系统计算模型(m)

表2 动力计算参数

以Imperial Valley-02地震(1940年，美国)中EI-Centro Array#9台站记录到的实测地震动作为平坦基岩表面上的设计地震动，设计地震动水平向和竖向位移分量，如图9所示。

(a) 水平向

3.2 二维基岩-覆盖层地基斜入射输入方法

通常，一般工程根据GB 18306—2015《中国地震动参数区划图》[16]确定设计地震动峰值加速度和场地特征周期，然后人工合成设计地震动。对于设防类别为甲类的重大工程，根据地震部门给出的场址危险性分析结果确定其设计地震动。这两种方法获得的设计地震动均是指工程场地所在地区半无限空间均质岩体在平坦地表的地震动，为此，本文选取不受河谷地形影响的平坦基岩表面C点作为控制点，在C点所在的顺河向半无限基岩平面(平面1)内，利用本文所建立的方法(方法2)获得基岩地基底部入射波时程，然后将顺河向基岩平面空间(平面1)地基底部的斜入射波时程平移转换至基岩-覆盖层地基底部(平面2)，如图10所示。地震波入射方向与水流向是平行的，只产生平面内运动，在入射方向上不存在河谷地形散射效应。

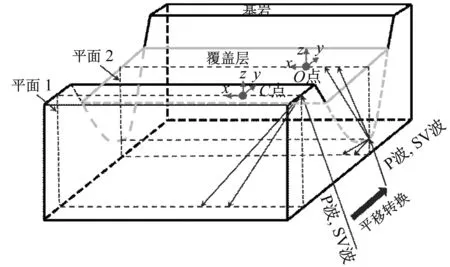
图10 基岩-覆盖层地基底部入射波时程获取方法示意图

基岩地基底部及上、下游侧采用黏弹性人工边界[17-21]结合等效结点荷载的地震波动输入。覆盖层土体在地震作用下具有明显的非线性特性[22]，无法通过解析方法获得覆盖层上、下游侧截断边界上的边界参数和等效结点荷载。为此，地基上、下游采用远域边界模拟辐射阻尼效应，远域地基的截取范围根据楼梦麟等[23-24]的研究结论，取地基深度的7倍，已经可以满足工程精度要求。

3.3 土石坝加速度反应

土石坝加速度的计算方案与前面自由场计算的方案一致，其中方法1包括P波斜入射和SV波斜入射两种情况。图11为两种方法获得的坝顶最大加速度以及方法1相对方法2的偏差。从图11可知，方法1 P波斜入射情况获得的坝顶水平向和竖向最大加速度与方法2有较大的差异，相对于方法2水平向和竖向加速度最大偏差分别为90.0%和53.0%，相对偏差均随入射角增大而减小。方法1 SV波斜入射情况计算得到的坝顶竖向最大加速度相对方法2偏差较大，最大偏差超过了70%，相对偏差随着入射角度增大先减小后增大；坝顶水平向最大加速度与方法2相近，原因是方法1中地表水平向地震动强度随角度变化小，与设计地震动水平分量接近。

(a) 水平向

从图11可知，方法2坝顶水平向和竖向最大加速度随入射角的增大而减小，原因从图12(建基面典型点位移时程，点1112和点2601分别位于上、下游坝角，点64位于坝轴线底部)可以得到解释，与垂直入射相比，地震波斜入射建基面任意两点地震动初至时间间隔增大，造成各点地面运动存在相位差(图12中15～20 s的放大位移时程)，地面运动呈现非一致性，减弱了坝体的同频共振。在位移峰值上，建基面典型点水平向位移峰值最大差异为12.5%，竖向位移峰值最大差异为25.0%。方法1由于控制点已经偏离了设计地震动峰值，所以其难以正确构建非一致地面运动，获得的坝顶加速度大小随角度变化的规律中包含着地震动幅值变化的贡献，无法分析基于设计地震动的入射角变化或者非一致地面运动对坝体响应的影响。

(a) 水平向

由此可见，在任意非垂直入射角度下，基岩地基底部斜入射波幅值取平坦地表水平向设计地震动幅值的一半得到的坝体地震响应不是设计地震动强度下的结果，并且与设计地震动下的计算结果偏差较大。考虑P波和SV波对坝址场地自由场的共同贡献，根据入射角确定斜入射波时程，可以获得的坝体非一致地震响应，能够在相同的设计地震动强度作用下，单纯分析入射角对坝体地震响应的影响规律。

图13和图14分别为方法2中土石坝1-1剖面和2-2剖面最大加速度分布。1-1剖面和2-2剖面的位置示意,如图8所示。从图13可知，土石坝1-1剖面水平向和竖向最大加速度随入射角的增大而减小，与0°入射角相比，当入射角为45°时水平向和竖向最大加速度减小幅度可达20.8%和31.1%。减小的原因是地震波斜入射引起建基面各点地震动出现相位差，减弱了覆盖层-土石坝系统的同频共振，入射角越大，相位差越大，地震动非一致性越显著。水平向和竖向最大加速度随高度的增加先减小后增大，在建基面附近，加速度最小，主要是覆盖层土体进入强非线性状态，阻尼耗散能力增强，强震作用下覆盖层对地震波有抑制作用。

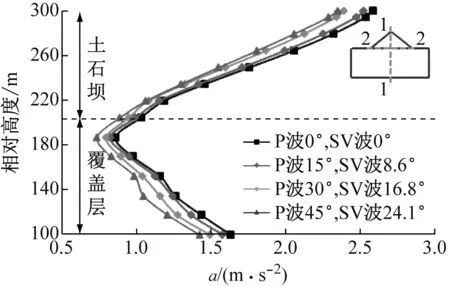
(a) 水平向

图14表明，土石坝2-2剖面(建基面)水平向和竖向最大加速度随入射角的增大而减小，与0°入射角相比，当入射角为45°时水平向和竖向最大加速度最大减小幅度分别为27.8%和25.9%。由于上游静水压力的作用，覆盖层-土石坝系统上游侧震前围压大于下游侧，导致建基面上游侧水平向加速度小于下游侧，随着入射角度增大，上下游侧加速度差距更明显，最小加速度位置逐渐向坝中心移动。上游静水压力对竖向加速度的分布规律影响较小，建基面上竖向加速度关于坝体中心对称分布，坝中心位置竖向加速度最小。

(a) 水平向

4 结 论

本文分析了当前基岩地基底部斜入射波时程的确定方法和适用性，基于设计地震动建立了P波和SV波组合斜入射时程相对于入射角度的函数关系式，实现了入射波时程随入射角变化，研究了不同斜入射波时程确定方法对半无限均质空间自由场和基岩-覆盖层-土石坝系统地震响应的影响。结论如下：

(1) 考虑P波和SV波对半无限空间自由场的共同作用，利用入射P波和SV波时程表示了空间任意点自由场，根据控制点自由场分量与设计地震动对应分量相同的原则，建立了斜入射波时程相对于入射角的函数关系式，确定了随入射角变化的入射波时程。研究了斜入射波幅值取设计地震动幅值的1/2和本文方法下的半无限空间自由表面的位移响应，斜入射波幅值取设计地震动幅值的1/2时，地表位移峰值相对设计地震动有较大误差，该方法不能应用于确定设计地震动强度下的斜入射波时程。本文方法获得的地表位移响应与设计地震动吻合，验证了本文方法的合理性。

(2) 在任意非垂直入射角度下，基岩地基底部入射波幅值取设计地震动幅值的1/2，获得的土石坝地震响应不是设计地震动强度下的结果，坝顶加速度大小随角度变化的规律中包含着地震动强度变化的贡献，与设计地震动强度下的计算结果有较大偏差，无法分析基于设计地震动的入射角变化或者非一致地面运动对坝体响应的影响。

(3) 本文提出的根据入射角确定斜入射波时程的方法，考虑了P波和SV波对坝址场地自由场的共同贡献，能够在相同的设计地震动强度作用下，正确反映斜入射角度引起的建基面的非一致运动，可以单纯分析斜入射角度对土石坝地震响应的影响。分析结果表明，土石坝加速度反应随入射角的增大而减小，主要原因是入射角增大，建基面振动方向相位差增大，各位置点运动呈现出非一致现象，减弱了坝体同频共振的趋势。