基于多源实测数据的RC结构基本周期统计分析

王泽涛， 陈 隽,2， 申家旭

(1.同济大学 土木工程学院，上海 200092；2.同济大学 土木工程防灾国家重点实验室，上海 200092)

钢筋混凝土(reinforced concrete，RC)结构应用广泛，其基本周期是固有的力学特性，也是开展结构动力分析、抗震评估以及参数化建模时的重要指标，能综合反映结构的刚度和质量特性[1]。基本周期值显著影响结构在风和地震等动力作用下的反应，因此，结构设计时一般要使其基本周期远离强迫荷载的周期或场地卓越周期，避开共振或类共振效应，减小结构的动力响应。然而，对于新建结构，在结构细部设计尚未完成的条件下，其基本周期很难通过理论分析获得足够精确的值。此外，对城市中的已建结构开展抗灾评估和参数化建模时，往往必须以结构几何参数(建筑几何形状、平面尺寸、高度、层数等)、结构体系、建筑材料等可获取信息为基础，确定建筑的动力性能。因此，研究RC结构基本周期的统计特性，依靠其结构高度或平面尺寸等宏观参数估算其基本周期，则可在初步设计阶段总体把握结构的刚度和质量是否适当，为结构设计方案备选调整提供便利，同时可为已建结构的抗灾评估提供建模依据。

鉴于RC结构基本周期的合理取值在工程设计与评估中的重要性，国内外学者很早就开始研究此问题。主要采用两种研究方法：一种是理论分析方法，如顶点位移法、能量法、刚度法[2]等；另一种是基于实测值的统计分析。理论分析方法的力学基础完善，但需要对材料、构件、结构的物理特性进行必要的简化或引入为假设。相比之下，实测值显然能更准确地反映结构的实际特性，特别是在大量数据支撑的统计意义上。例如，Satake等[3]将日本的25栋RC建筑和43栋钢框架-钢筋混凝土(steel reinforced concrete，SRC)建筑视为同一类样本，统计分析了其基本周期实测值的分布规律。国内学者对钢筋混凝土建筑的经验计算公式也进行过大量实测研究。漆桂芬[4]对国内的32栋RC建筑基本周期进行了脉动法实测，并给出了相应的经验公式。此后，王广军[5]、施卫星等[6]、那仁满都拉等[7]也开展了实测研究工作。上述工作都提出非常有价值的成果，同时也都指明了需进一步改进的问题，主要包括：①由于研究所固有的统计特质，增大实测数据量始终具有重要意义，需要不断更新；②伴随数据量的增大，可讨论不同方向或参数的影响，如明确区分结构长轴与短轴(或纵轴与横轴)的基本周期特性；③讨论不同国家/地区结构特性的差异；④引入新的数据分析手段，检验数据的可整合性能，深入挖掘数据中所蕴含的价值。

针对上述问题，本文在学习、吸收大量已有工作的基础上，系统性收集了文献中多国、多地区的RC结构实测周期值，显著扩充了样本数量。进而采用聚类分析方法对样本集进行子类划分，利用分类高度限值结果说明数据集的代表性及可整合性。基于不同的变量因子得出基本周期值随结构几何参数的变化规律，并将基本周期的回归公式与现有规范、文献中的公式进行比较。通过数据库中部分样本的对比分析，阐述了RC结构总体数据库中部分子类分布规律的差异性及其成因。

1 RC结构基本周期经验公式

建筑物的自振周期不仅与主体结构的质量和抗侧刚度有关，还受非结构构件(如填充墙的刚度贡献，楼梯间的位置分布等)、节点连接形式、建筑材料、场地条件以及土-结构相互作用等多种因素的影响。通过理论计算或现场测试，并对分析或测试数据进行统计回归提出经验公式，是分析特定结构自振周期分布规律的常用方式。

从20世纪60年代开始至今，国内外学者对RC结构基本周期的计算开展了持续的研究，提出了大量的经验公式，部分研究成果逐步形成了各国历届规范中的经验公式[8]。对于多层和高层RC结构，表1总结了国内外规范中应用范围较广的经验公式；表2则列举出来部分学者利用实测数据给出的拟合公式、结构所在国家(地区)以及样本数量。需要指出，规范的经验公式通常用于确定(偏于保守的)地震基底剪力设计值，往往对实测样本的最佳拟合公式系数进行了调整。

表1和表2中的基本周期经验公式可以分为两类：一类是单参数，往往以结构的高度或层数为变量因子；另一类是双参数，往往以结构的高度和平面宽度共同作为变量因子。此外，表2中基于实测数据公式的最大数据量为244栋RC建筑，位于意大利、斯洛文尼亚、克罗地亚和马其顿共和国4个欧洲国家[9]。

表1 国内外规范中基本周期经验公式

表2 不同学者提出的基本周期经验公式

2 RC结构周期实测数据库

2.1 实测数据来源

通过广泛文献检索，多渠道收集并建立了包含873栋高度100 m以下的RC结构的基本周期实测数据库。数据库中建筑的结构高度最低为3 m，最高为99.6 m(对应建筑层数29层)；建筑层数最低为1层，最高为34层(对应结构高度为97.2 m)。其中609幢建筑包含长轴、短轴两个正交方向的基本自振周期的实测值，因此获得了长短两轴共1 482个基本周期实测值。数据库中的RC结构体系包括框架结构，框架-剪力墙结构，剪力墙结构等，不包括钢筋混凝土核心筒体系。下面是本文数据库的数据来源的简要描述。

(1) Goel等[12]记录了美国27栋RC框架在真实地震下的长短两轴的基本周期，其中8栋位于地震动峰值加速度不小于0.15g的高烈度地震区，8栋包含2次或3次观测记录。该文献采用真实地震动下的结构响应进行周期的识别，由于结构振幅大，一般实测周期会略高。

(2) Lee等[13]对韩国境内50栋RC剪力墙结构进行了环境激励测试，记录了长短两轴的基本周期。

(3) Gallipoli等对4个欧洲国家共244栋RC建筑进行环境振动测试，记录了长短两轴的基本周期，其中65栋位于意大利，47栋位于斯洛文尼亚，62栋位于克罗地亚，70栋位于马其顿共和国。

(4) Pan等[14]总结了对新加坡116栋高层RC住宅建筑的环境振动测试值，并记录了19栋受远场地震影响的RC建筑基本周期观测值。文献未提供结构高度，本文后续分析按照底层3.6 m、其他楼层2.8 m层高估算结构高度。同时，文献未具体说明实测值方向，基于文章内容判断，一律视为结构短轴基本周期。

(5) 日本建筑学会[23](architectural institute of Japan, AIJ)收集了日本137栋钢框架结构，43栋钢框架-钢筋混凝土结构和25栋RC结构在多种激励方式下的模态测试结果，记录了长短两轴的基本周期值。本文选用了其中的25幢RC结构的实测数据，其中6栋包含2次及以上的观测记录。

(6) 王广军等[24]在《建筑自振周期计算方法和实测资料手册》中收录了246栋中国多地的RC结构实测周期信息，其中175栋RC框架，32栋RC现浇壁板结构，18栋RC框剪结构，21栋RC剪力墙结构。

(7) 施卫星等总结了对上海31栋RC框架的环境激励测试结果，利用自行研发的结构振动信号采集分析系统获得了建筑物长短两轴的一阶自振频率。

(8) Ho等[25]对日本福冈的22栋RC建筑、2011年7—8月对中国呼和浩特的36栋RC建筑实施环境激励测试，记录了长短两轴的基本周期。

(9) 其余实测数据包括：胡进军等[26]对中国云南省16栋高层RC建筑的环境振动测试结果(本文全部视为短轴基本周期)；刘红彪等[27]对中国西昌市9栋RC结构、吴伟达[28]对中国福州市20栋RC结构以及任旋[29]对中国福州市21栋RC结构，均采用脉动法测试获得了结构的长短轴基本周期。

2.2 实测数据预处理和特性分析

首先对以上9个源数据库的实测信息进行预处理：统一以周期形式记录；对包含多次观测记录的建筑取其平均值作为代表周期；删去7个结构高度超过100 m和2个缺少高度及层数的数据，最终共收录873栋100 m以下的RC结构的1 482个周期样本。图1对数据库样本进行了可视化展示，分别将其按样本点所属源数据库(见图1(a))以及“周期-高度关系”对应的方向(见图1(b))进行分类；并将0～100 m高度等分为10个区间，统计了数据库中各高度区段包含的RC建筑数量和比例，结果如图2所示。由图2可知，超过60%的样本分布在10～40 m高度内，约20%的样本分布在40～60 m高度内。

(a) 不同学者的实测周期

图2 数据库中RC结构的高度区间分布

多个数据来源是大样本数据库建立的必然途径，因此有必要对多源数据的特性进行讨论。图1中除方框内数据外呈现出一致趋势，其图1中方框内数据(Lee等和Goel等的数据)则具有不同的特征：样本点分布呈现出在同一高度，结构基本周期有较大范围的变化，尤其在40～80 m高度区段。因此，后续分析中将Lee等和Goel等的数据作为对比数据集，其余数据则视作一类数据，作为拟合周期公式所用的样本，并称为分析数据集。

3 数据样本的聚类分析

当RC建筑超过一定高度后，需要调整其结构体系以满足相关设计规范的要求。例如，按照JGJ 3—2010《高层建筑混凝土结构技术规程》(简称《高规》)[30]的规定，高层RC建筑是指10层及10层以上或房屋高度大于28 m的住宅建筑以及房屋高度大于24 m的其他民用建筑混凝土结构。图1(b)在数据集中标识了此两条高度界限。

当RC结构基本周期记录数据足够多时，可采用不同的分类方法并依据数据的某一属性对实测周期样本进行归类。聚类分析是无监督机器学习中的一种，该方法就是把一组数据按照相似性归成若干类别，使属于同一类别的数据间的距离尽可能最小，属于不同类别的数据间的距离也尽可能最大[31]。聚类分析无需先验信息，可作为实测数据代表性的一种检测方式。聚类方法有多种，本文采用K均值聚类方法，该方法是典型的基于距离的聚类分析，采用距离作为相似性的评价指标，认为两个对象的距离越近，相似度就越大；由距离靠近的对象组成类，将紧凑且独立的类作为分析结果。K 均值聚类方法的具体步骤如下，设定样本集的聚类簇数为m类时：

步骤1随机选择m个样本点，每个样本点代表一个子类的初始聚类中心点；

步骤2对除聚类中心点之外的所有样本点逐个归类，按照所设定的距离指标，将每个样本点归入与它距离最小的聚类中心所在的簇，直到所有样本点都归类结束，初始分类完成；

步骤3重新计算m个初始分类中样本点的均值，作为新的样本聚类中心点，按照上述步骤2的计算方法，对每个样本点重新归类，每类的样本数据会发生调整，调整后的每类样本的均值为该类的新聚类中心点；

步骤4重复步骤3，直到每类的样本数据都不再发生变化，得到最终的分类结果。

常用的距离指标有欧氏距离、曼哈顿距离、闵可夫斯基距离等，这里用曼哈顿距离，即两个向量各分量差的绝对值之和作为距离评价指标，两个n维向量xs=(a1,a2,…,an)和xt=(b1,b2,…,bn)之间的距离可表示[32]为

(1)

如图3所示，对分析数据集内的周期样本点在全域高度下执行聚类分析。当设置类别为两类时(见图3(a))，聚类中心点坐标依次为第一类(0.32 s,20 m)、第二类(0.70 s,45 m)，取第一类(黑色空心圆点)样本点中的最大高度与第二类(空心菱形点)样本点中的最小高度的平均值作为聚类分析的高度分界线，则高度分界线为32.375 m，与《高规》中多层和高层住宅建筑的分界高度较为接近；设置类别为三类时(见图3(b))，同理可得，聚类中心点坐标依次为第一类(0.99 s,61 m)、第二类(0.53 s,34 m)、第三类(0.29 s,18 m)，聚类分析的第一条高度分界线为26.05 m，与《高规》中一般建筑的多层和高层分界线极为接近。结合分析数据集中的RC结构多具有较为简单的平面形状，聚类分析的结果进一步说明本文数据库中的多源实测样本可以代表典型的RC建筑结构。

(a) 类别设置为2类

4 基本周期与几何参数回归分析

4.1 单参数回归分析

4.1.1 拟合方法与评价指标

从第1章可知，应用最为广泛的结构基本周期—高度公式为T=CHx型，T为周期，H为结构高度，C为待定系数，x为幂指数，其产生的理论根据是瑞雷法。对于一定高度的建筑，采用瑞雷法推导其基本周期时，首先做如下4点假设：等效水平力沿结构高度方向线性分布；地震基底剪力与参数1/Tγ成比例；结构质量沿其高度均匀分布；在水平均布力作用下结构变形沿建筑高度呈线性变化，各层层间位移角相同。基于上述4条假设，可导出

T=α1H1/(2-γ)

(2)

式中:T为基本周期,s；H指结构高度,m；α1和γ为常参数，可依据不同的样本集拟合得出。

为方便使用，本文在γ=1的情形下进行约束拟合，产生结构周期—高度的线性拟合公式，并参照文献[33]中对智利建筑采用的结构概念分类方法，采用“三直线”回归模型，在给出最佳拟合公式的基础上进一步给出“偏刚”和“偏柔”情形下的拟合公式。具体做法是首先对长轴或短轴全部样本点进行最小二乘回归，将落在回归直线下方和上方的数据点视为两个单独的集合，再分别进行最小二乘回归，即可得到3条回归直线。对于刚度较大的建筑，基本周期较小，则可采用下方直线进行估算；反之对于刚度较小的建筑，则可采用上方直线进行估算。

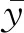
(3)

4.1.2 基本周期与结构高度的关系

本节对分析数据集中的RC建筑长轴(见图4(a))和短轴基本周期(见图4(b))与结构高度的关系分别进行最小二乘回归。数据库中，对应长轴周期的有效样本点有562个，短轴周期的有效样本点有792个，均远远多于此前研究的样本量。指定回归形式为T=α1H，拟合结果如表3所示。本文所有周期拟合结果的量纲均为s。

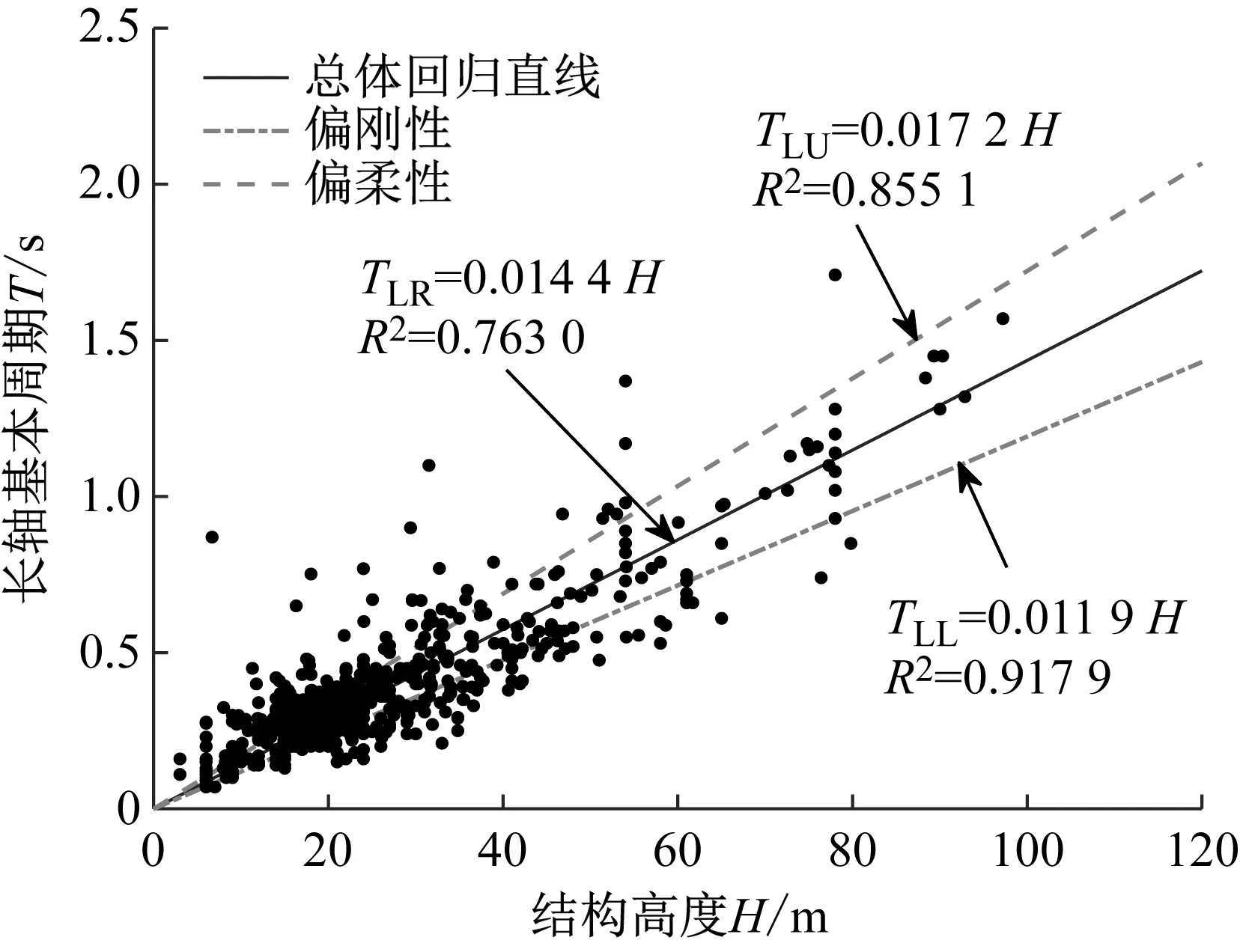
(a) 长轴周期-高度

RC建筑的长轴平面通常包含更大的抗侧力面积和更多的抗侧力体系，刚度较短轴一般更大，从而基本周期略小于短轴。由拟合结果看，长轴方向各拟合系数均小于短轴方向对应系数，也符合结构动力学的基本概念。对比Satake等和施卫星等对结构动力特性实测值的拟合经验，其决定系数在0.6～0.8。表3中各拟合公式的决定系数均已达到较大值，因此在缺乏更多结构信息的情形下，推荐采用总体回归直线(刚柔性)方程进行基本周期的估算。结合表2对比，本文长轴总体回归直线TL=0.014 4H与黄真萍等的长轴拟合结果极为接近，短轴总体回归直线TS=0.016 6H与Gallipoli等的预测模型相当接近。如果以“偏刚性”和“偏柔性”对应的直线分别作为预测区间的下限和上限，则长轴预测区间为TL=(0.011 9～0.017 2)H，下限最接近于徐培福等，上限最接近于Lagomarsino；短轴预测区间为TS=(0.014 4～0.019 5)H，下限同样最接近于黄真萍等，上限最接近于Gilles等。

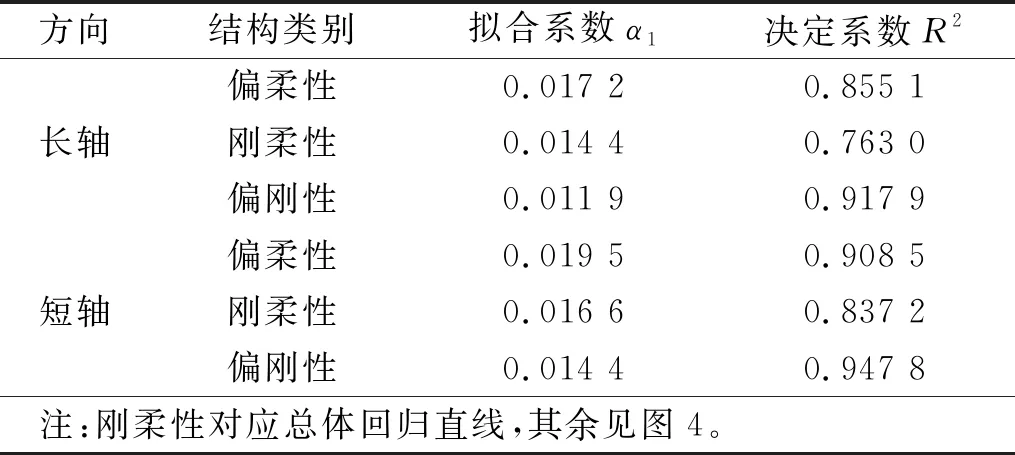
表3 基本周期与高度拟合结果

4.1.3 基本周期与结构层数的关系

本节对分析数据集中的RC建筑长轴(见图5(a))和短轴基本周期(见图5(b))与结构层数的关系进行了回归分析，方法同4.1.2节。数据库中，对应长轴方向的有效样本点有190个，短轴方向的有效样本点有344个，指定回归形式为T=α2n，拟合结果如表4所示。考虑到结构初步设计阶段有时层高并未确定，且结构层数较之高度是一个无量纲数，而且它包含了一个重要的结构动力学特性——楼层质点数量[35]，故相比于以结构高度作为RC建筑的竖向几何参数，采用结构层数n来替代结构高度H有时更加直观和方便。对长短两轴拟合结果的分析和说明则与4.1.2节同理，不再赘述。结合表2对比，本文长轴总体回归直线TL=0.042 4n与Michel等的拟合结果相当接近，而短轴总体回归直线TS=0.048 6n与Navarro等的预测模型极为接近。

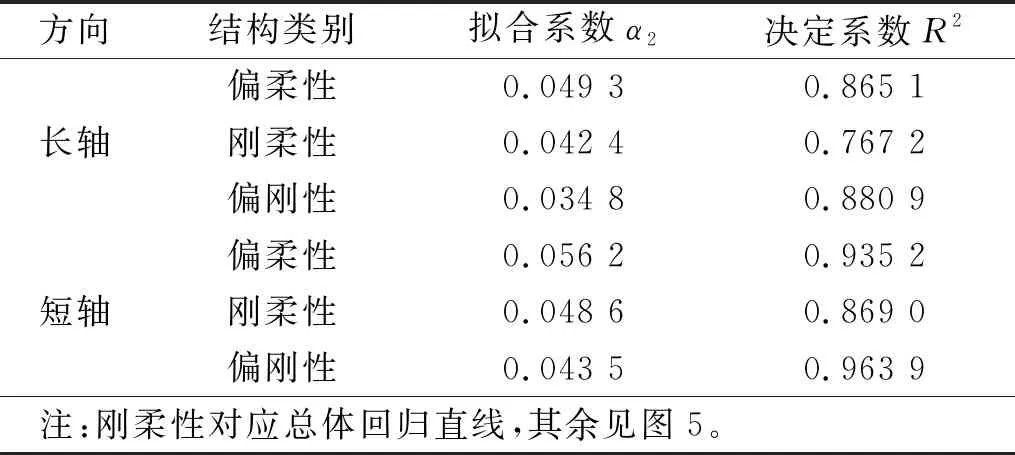
表4 基本周期与层数拟合结果

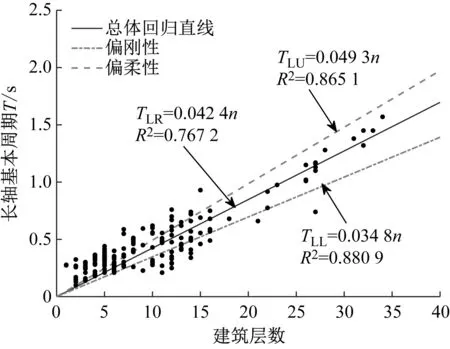
(a) 长轴周期与层数

4.2 双参数回归分析

除去单参数分析，同时采用竖向和平面双几何参数进行回归分析也是常见的方式。以结构高度与平面宽度为变量因子的经验公式，最初是根据王明振等测得的142条含有黏土砖填充墙的框架结构实测周期数据，采用最小二乘法拟合而来。以此为基础，本节指定的双参数拟合形式为

(4)

式中:T为结构基本周期,s；X为结构平面尺寸,m，考虑到为平面快速建模提供便利，拟合长轴和短轴时，分别采用平面长度L,m;平面宽度B,m；α3,α4,β,λ为待定拟合系数。

首先按GB 50009—2012《建筑结构荷载规范》的形式，指定β=2,λ=1/3进行约束回归，数据库中，对应长轴高宽比的有效样本点有285个，短轴高宽比的有效样本点有293个，进而得到结构长轴(见图6(a))和短轴(见图6(b))基本周期与结构“高宽比”的最佳拟合方程为

(5)

(6)

式中:TL和TS分别为长轴和短轴基本周期；H为结构高度；L为结构平面长度；B为结构平面宽度。如图6所示，给出了决定系数R2和标准差σ，并在回归直线两侧绘制了偏差为±1σ和±2σ的条带域以便直观地反映变异性。从结果上看，R2已经达到较大值，且拟合系数与GB 50009—2012《建筑结构荷载规范》相当接近，相较表2中王广军和施卫星等的同一形式的经验公式，本文长短两轴的预测周期均偏低。在此基础上，进一步尝试在指定α4=0而对其余拟合系数不做约束的情形下进行回归，得到

(7)

(8)

对比图6可以发现，式(7)和式(8)的拟合优度基本不变，但公式复杂度显著上升；且L和B的幂次差距相当明显，不便于统一应用，故不推荐采用类似式(7)、式(8)的经验公式。

(a) 长轴周期-高宽比

5 数据集差异性分析

随着数据来源途径的增加和数据库中样本数量的扩充，部分子类往往会呈现出不一致的分布趋势，掌握数据库中部分子类样本的差异特征及其成因，对数据库进一步纳入更多的观测数据有着重要的参考价值。Goel等和Lee等在拟合实测周期值的过程中，均未区分长短轴而是将两正交方向的周期值一并拟合以增加数据量，为方便对照，这里沿用上述方法并结合本文的拟合公式，对数据库中对比数据集的差异特征及其成因进行探讨。

如图7所示，在相同高度下，本文的拟合结果相较于Goel等的实测周期值和预测值均偏小且差距较大。两个可能的原因是:①Goel等的实测周期均是在真实地震作用下经由安装在RC建筑内部的加速度计获得的，而RC结构中的混凝土构件在地震中不可避免地会产生和开展裂缝，造成结构抗侧刚度的下降；②由于中美设计规范要求与结构体系(包括少分隔墙的建筑布置风格等)存在差异。

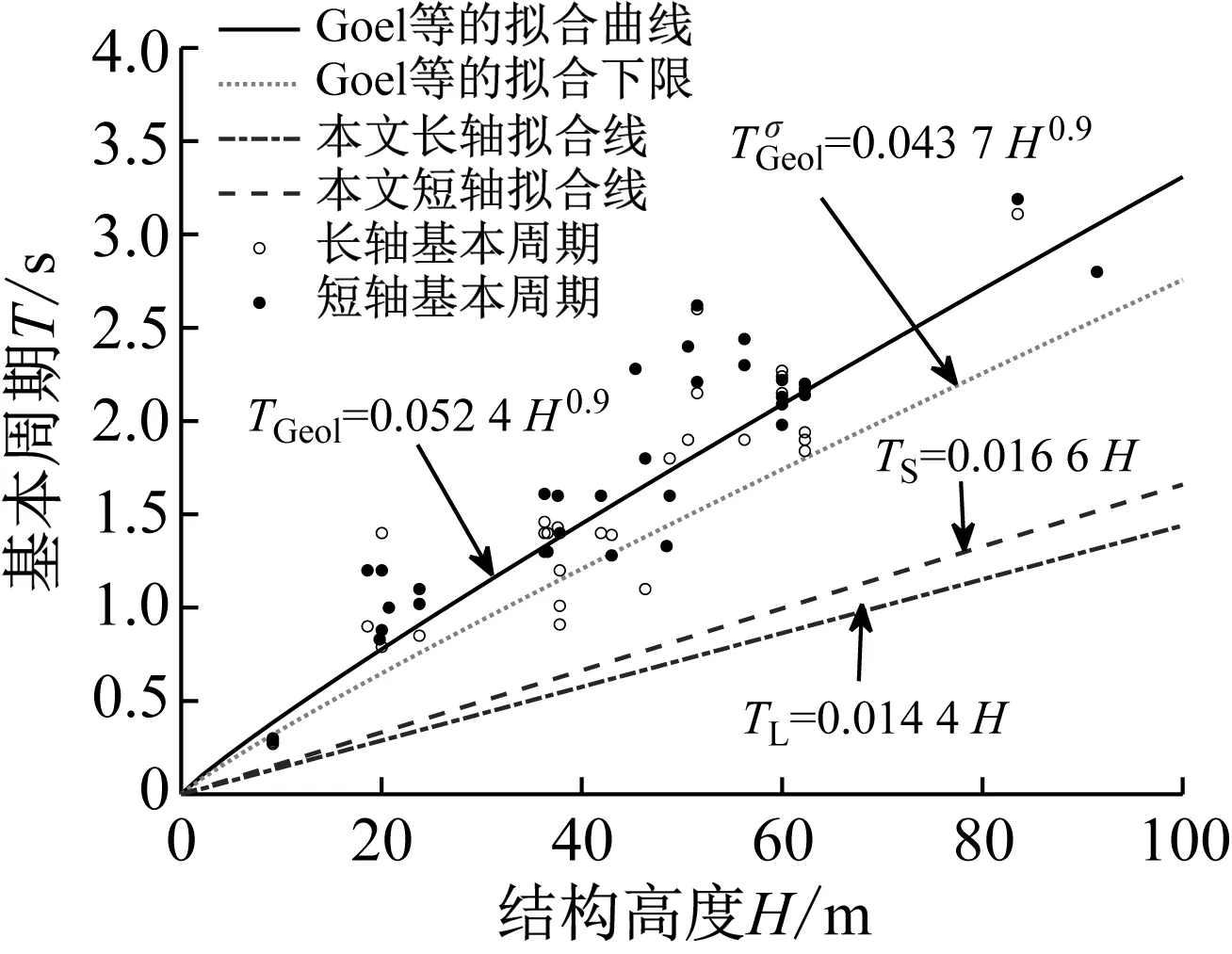
图7 Goel等的拟合公式与本文的对比

进一步将Goel等和Lee等的实测周期数据归并在一起进行对照和回归，结果如图8所示。在指定拟合形式为T=CHx的情形下，得到回归曲线为

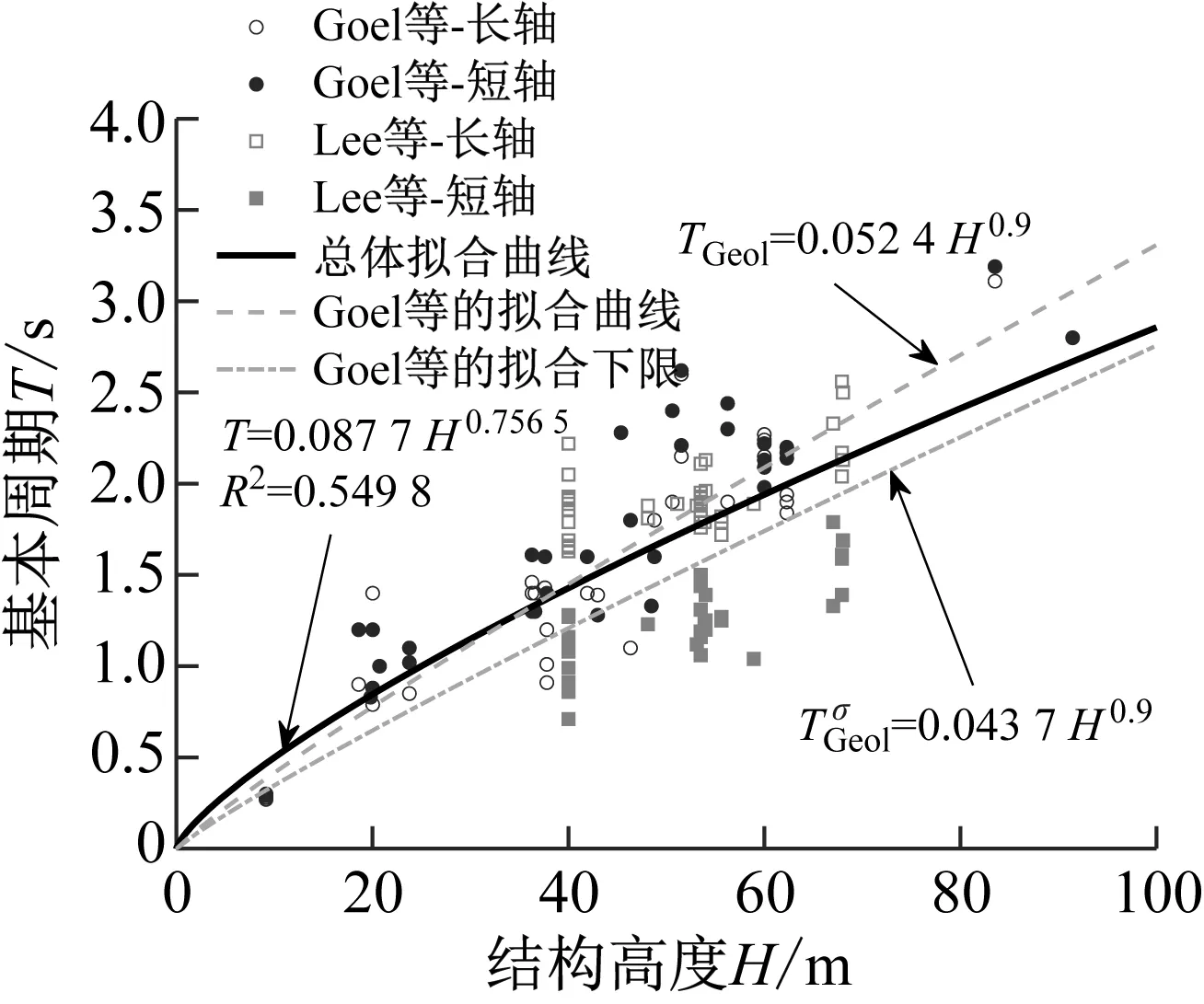
图8 Goel等和Lee等的拟合公式对比

T=0.087 7H0.756 5

(9)

与Goel等所给的另一替代公式T=0.110 7H0.75较为接近，但决定系数R2=0.549 8却较小。这是因为Lee等的实测样本高度集中在40 m，48 m，54 m和67 m附近，但长轴或短轴基本周期却在相当大的范围内变化，数据的离散程度非常高。相较于本文的周期-高度拟合直线，反映出Lee等实测的RC建筑呈现“偏柔性”的特点。

对Lee等提供的实测数据，本文经过多种拟合方式的尝试后发现，除Lee等给出的拟合方式,如图9所示。其余所有常用经验公式的拟合结果对样本点的可解释性均不够强。图9中Lw为结构平面单位面积内剪力墙墙肢平均长度(区分长短轴)，其余字母含义同前文。

结合图9和Lee等的数据列表进一步观察Lee等对韩国的50栋RC剪力墙结构测得的周期样本可以发现，其中22栋仅给出一个方向的基本周期，剩余28栋给出长轴和短轴两向的基本周期，但均是长轴基本周期大于短轴基本周期。这与以往的经验、本文数据库中其余学者实测数据的一般情况以及本文的拟合结果恰恰相反。造成这种特殊现象的原因是：韩国的50栋RC剪力墙结构中长轴方向平面单位面积内剪力墙墙肢平均长度比短轴小的结构为49栋，其中长轴-短轴平面单位面积内剪力墙墙肢平均长度比值小于等于0.6的数量为35栋，从而导致长轴抗侧刚度普遍小于短轴。图9也说明了针对RC剪力墙结构的经验公式可能与其余RC结构有不同形式，在数据量支持的情况下应纳入更多的影响因子(尤其是剪力墙的位置分布和面积占比)做进一步的研究。

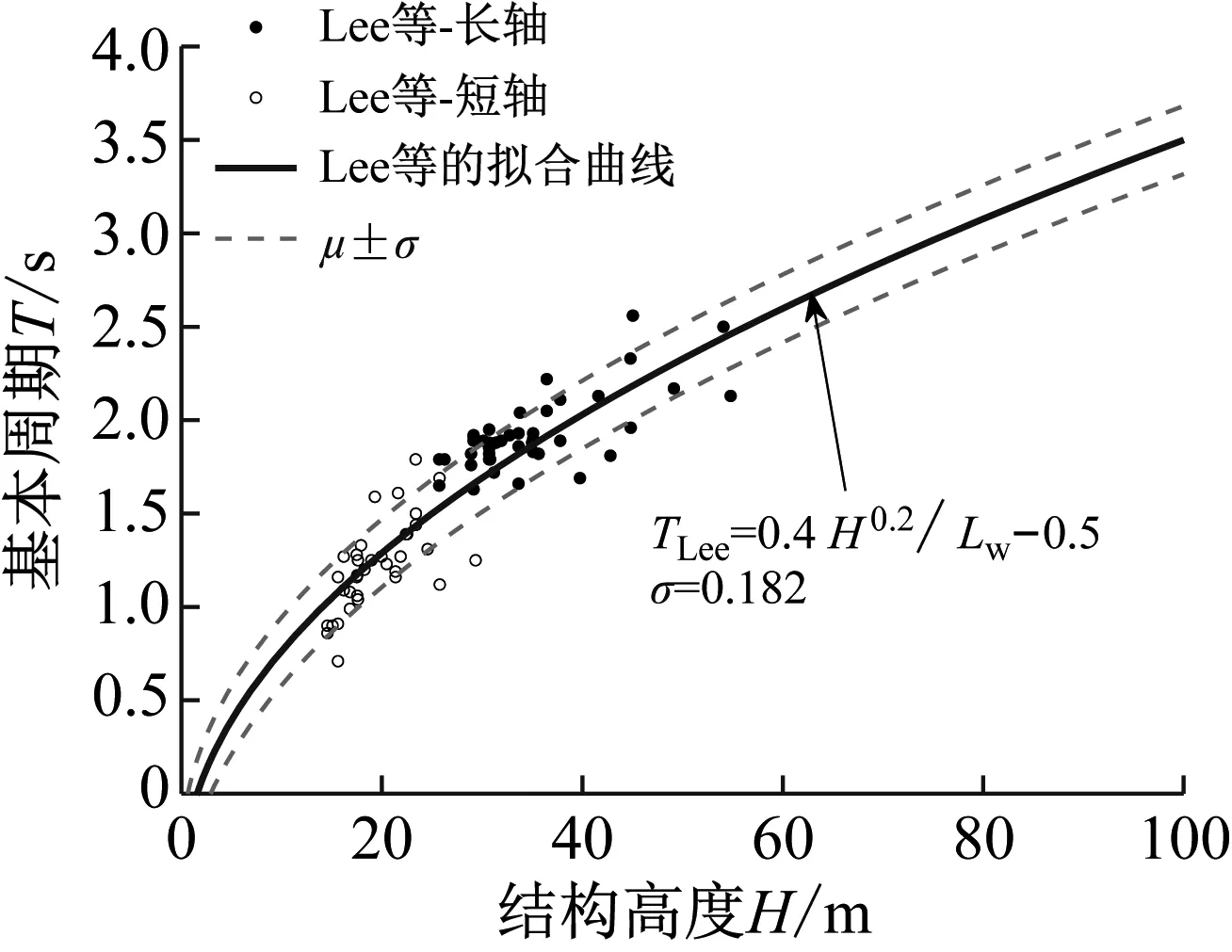
图9 Lee等的拟合公式

6 结 论

本文以钢筋混凝土结构的基本周期为研究对象，归纳了典型形式的基本周期经验公式，吸收总结了大量已有的研究工作的宝贵经验和成果，以实测数据为基础对RC结构的基本周期分布规律得到了进一步的认识。

(1) 利用大量的实测信息作为样本，通过873栋100 m以下高度的RC结构的1 482个基本周期数据点，研究了钢筋混凝土结构基本周期的分布规律，考虑多个几何参数的影响，分别以结构高度、结构层数、结构高宽比为变量因子进行回归分析，给出了不同形式下的经验公式。实测数据量的扩大增加了本文拟合结果的精度和可靠性。

(2) 通过数据对比，讨论了数据库中对比数据集的差异特征，并分析了造成差异的原因，对数据库进一步纳入更多的观测数据有着重要的参考价值。

(3) 建筑结构自振周期经验公式的确定，既需要更多的场地实测信息支撑，又需要更优越的理论分析手段，这将是一个长期逐步深入的过程。进入数据时代，实测信息成为RC结构自振周期规律研究新的推动力量。然而，研究过程发现，相关数据资源还存在整合度差、碎片化严重、共享程度低的问题，阻碍了数据价值的深度挖掘和有效利用。为此，本文数据库将伴随文章同步发表，实现数据的共享。