基于导波多点散射的在役拱桥吊杆腐蚀损伤识别
2021-10-18朱劲松林阳子官幼平
陈 鑫, 朱劲松, 林阳子, 官幼平
(1.天津大学 建筑工程学院,天津 300072;2.中铁大桥科学研究院有限公司,武汉 430034;3.广东荣骏建设工程检测股份有限公司,广州 528251;4.深圳市索杆桥梁工程检测有限公司,广东 深圳 518000)
吊杆作为上、中承式拱桥的主要受力构件,其健康状况直接影响结构的安全性与耐久性。吊杆长期暴露在空气中,极易受水、空气及腐蚀性介质侵蚀而产生腐蚀,给桥梁结构带来重大隐患[1-2]。近年来,桥梁在运营过程中吊杆突然断裂的重大安全事故时有发生[3],及时、有效的进行吊杆腐蚀评估是保障在役桥梁结构健康与安全的关键问题之一。
目前,在役吊杆腐蚀还没有可靠的的无损检测方法。常规的无损检测方法,如超声法[4]、漏磁法[5]等,必须贴近待测索体表面,沿其长度方向逐点扫描,存在效率低、成本高、劳动强度大等问题。近年来,基于超声导波的无损检测方法得到了广泛关注。与传统超声检测中使用的体波不同,导波由弹性波在波导介质边界处多次反射形成,克服了传统检测需要沿长度方向逐点扫描的缺点,在识别结构裂纹[6-7]、黏结界面剥离[8]及板材脱层损伤[9]等方面得到了广泛应用。
腐蚀是吊杆中最常见的病害,也是造成索内钢丝断裂的主要诱因。随着腐蚀程度的加剧,吊杆有效截面减小,局部状态显著恶化。由于截面的不连续,导波在传播至损伤处时发生散射,形成导波检测中常用到的缺陷回波。Scalea等[10]在钢绞线中设置人工缺陷模拟局部损伤,通过导波缺陷回波较好的识别出钢绞线损伤。Rizzo等[11]采用缺陷回波的相关小波变换系数构建损伤指标,通过对损伤指标进行离群分析,对钢绞线局部损伤进行了量化。Gaul等[12]采用有限元与边界元研究了导波在钢绞线局部缺陷处的相互作用。何存富等[13-14]采用小波降噪和多通道时间反转聚焦增强检测信号信噪比和缺陷回波能量,有效提高了超声导波在钢绞线缺陷检测中的精度与敏感性。林阳子等[15-16]研究了磁致伸缩导波在桥梁缆索缺陷检测中的应用,分析了缺陷位置、不锈钢护套等因素的影响。潘永东等[17]采用高频纵向导波识别拉索锚固区损伤,将缺陷回波反射系数作为识别指标评估损伤程度。众多研究成果表明,利用导波缺陷回波可以有效识别局部损伤。然而,以往一些钢绞线、缆索导波检测结果多针对局部裂纹,对于难以辨别局部缺陷回波的在役拱桥吊杆多点腐蚀无参考识别且研究较少,往往需要健康状态下的基准数据作为参考[18-19]。
本文采用低频纵向导波在吊杆腐蚀处的多点散射特征进行吊杆腐蚀损伤识别。首先,通过引入分形函数模拟钢丝锈蚀表面,建立了多点腐蚀钢丝的有限元模型,对不同腐蚀程度下的导波传播过程进行数值模拟。然后,通过小波变换提取多点散射回波的多尺度能量谱,并将其作为特征向量构建腐蚀指标进行损伤识别,分析了导波频率的影响。最后,采用该方法对某拱桥吊杆进行现场检测,并进行现场开窗验证。该方法无需健康状态作为基准,可为在役吊杆锈蚀状况识别提供一种有效手段,具有较高的工程应用价值。
1 柱波导理论及导波多点散射特征提取
1.1 柱波导理论
高强钢丝是吊杆的基本组成单元,通过引入不同边界,可以求得不同模态导波频率特征方程的解析解。考虑材料衰减特性,自由边界无限长高强钢丝中纵向导波的Pochhammer频散方程[20]如式(1)所示
(1)
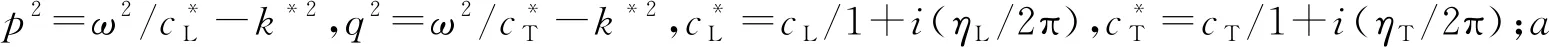
式(1)为超越方程,由MATLAB软件数值求解可得到纵向导波的f-k*曲线,根据式(2)、式(3),可以得到高强钢丝中纵向导波的群速度频散曲线和衰减频散曲线。
群速度
cg=dω/dkr
(2)
衰减值
α=ki
(3)
高强钢丝几何及材料参数如表1所示。纵向导波群速度频散曲线和衰减频散曲线,如图1、图2所示。
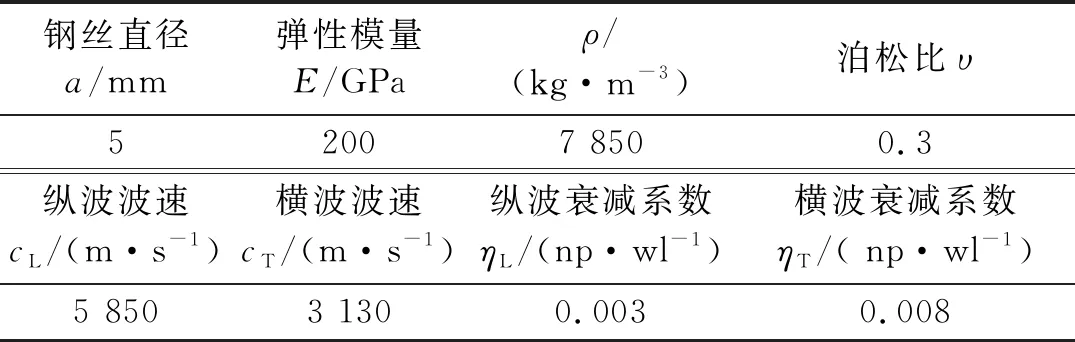
表1 高强钢丝几何及材料参数
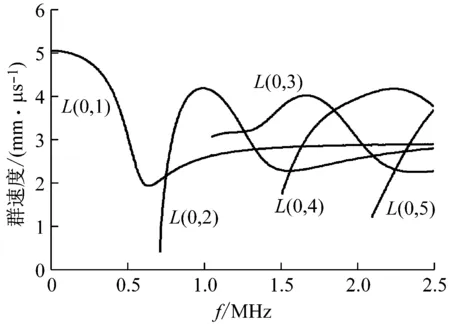
图1 纵向导波群速度频散曲线
由图1、图2可知,随着频率的增加,纵向导波在高强钢丝中的传播存在多种模态,不同模态、频率的导波可能波速接近,为导波的识别带来困难。不同频率、模态纵向导波的衰减特性差异明显。低频段的一阶纵向导波L(0,1)波速明显高于其他模态,易于识别,且衰减较小,十分适合桥梁拉索、吊杆等长距离索体结构的快速检测。由于高强钢丝的螺旋几何特征和相互接触对低频纵向导波影响较小[21-22],因此,理论分析与数值模拟中均未考虑螺旋几何特征和钢丝相互接触的影响。
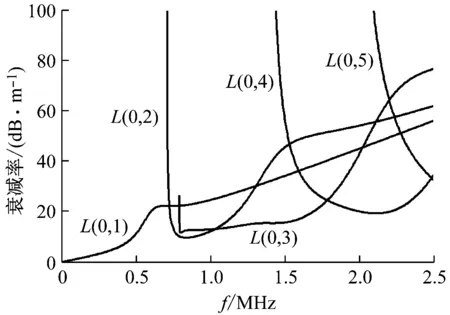
图2 纵向导波衰减频散曲线
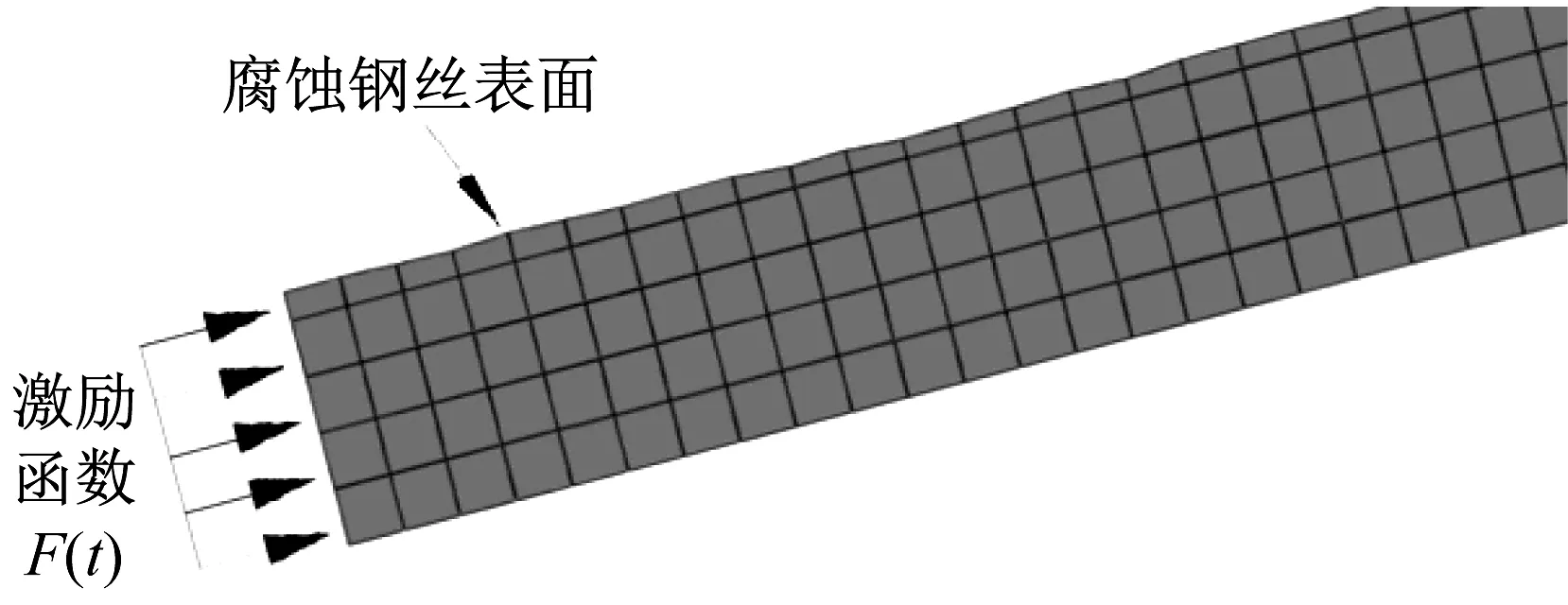
腐蚀损伤造成吊杆局部声阻抗的差异,使得导波在传播至腐蚀边缘时发生散射。实桥吊杆沿长度方向往往存在多处腐蚀,多个腐蚀回波相互叠加,形成能量分布较为平稳的多点散射回波。多点腐蚀吊杆中导波传播示意图,如图3所示。随着腐蚀程度的加剧,导波多点散射加强。通过分析腐蚀前后多点散射回波的特征差异可以有效识别吊杆腐蚀损伤。
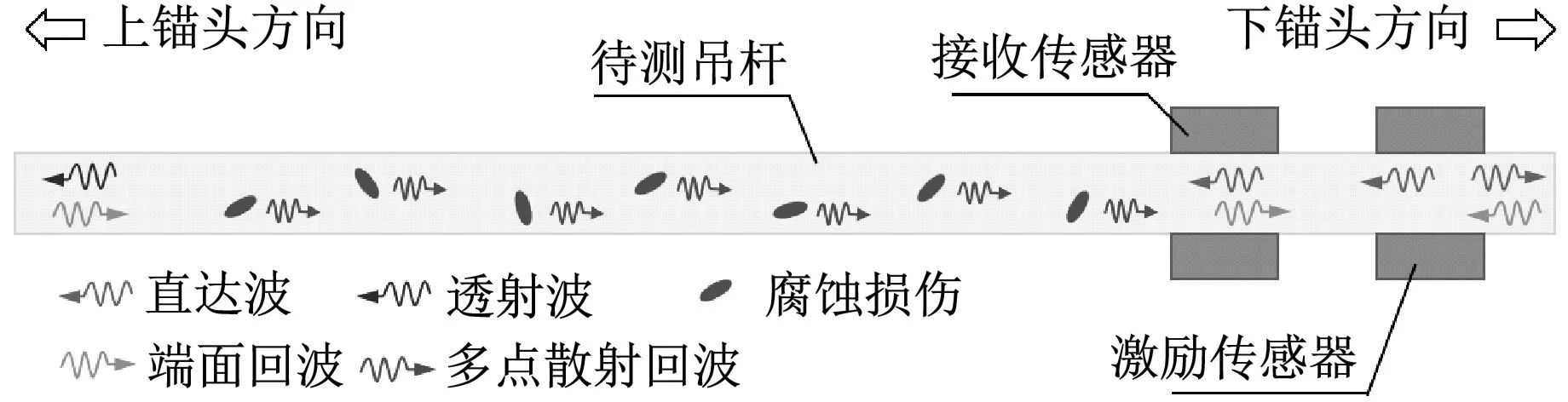
图3 多点腐蚀吊杆中导波传播示意图
1.2 导波多点散射特征提取
小波变换作为典型的非平稳信号处理方法,能够有效描述散射回波在时间-尺度域局部化特性,是一种有效的特征提取方法[23]。多点散射回波f(t)∈L(R)的连续小波变换可以定义为
(4)
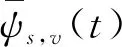
根据小波变换的等距性,即小波变换前后信号能量不变,则
(5)
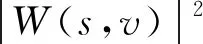
(6)
即
(7)
则多点散射回波各尺度能量在总能量中的分布,即多尺度能量谱I(s)可以表示为
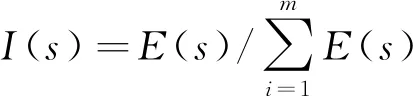
(8)
由于不同频率导波在多点腐蚀处的散射强弱存在差异,使得腐蚀前后,多点散射回波各尺度的能量分布发生变化。因此,本文将多点散射回波的多尺度能量谱I(s)作为特征向量构建腐蚀识别指标。
2 有限元模拟
2.1 有限元模型
采用ABAQUS软件模拟导波在多点腐蚀钢丝中的传播过程。钢丝长L=2 m,半径R=2.5 mm,不考虑阻尼的影响,材料参数见表1,采用轴对称单元建立高强钢丝的有限元模型。对于轴对称单元而言,每个波长40个计算节点可以比较精确的捕捉到波动效应,即
Δl≤λmin/(40-1)=CT/(39×fmax)=0.4 mm
(9)
式中:CT为材料横波波速;fmax为考虑高强钢丝中的最高频率成分,取200 kHz。
时间积分步长的取值应小于波在一个最小网格中传播所需要的时间,即
Δt≤Δtstable=Lmin/CL=6.8×10-8s
(10)
式中,Lmin,CT分别为最小单元尺寸、材料纵波波速。
因此,本文取单元尺寸Δl=0.4 mm,时间积分步长Δt=5×10-9s。
钢丝腐蚀是一个复杂的随机过程。已有研究表明,腐蚀表面具有明显的分形特征[24-25]。本文采用W-M分形函数[26]来模拟钢丝腐蚀表面,公式为
(11)
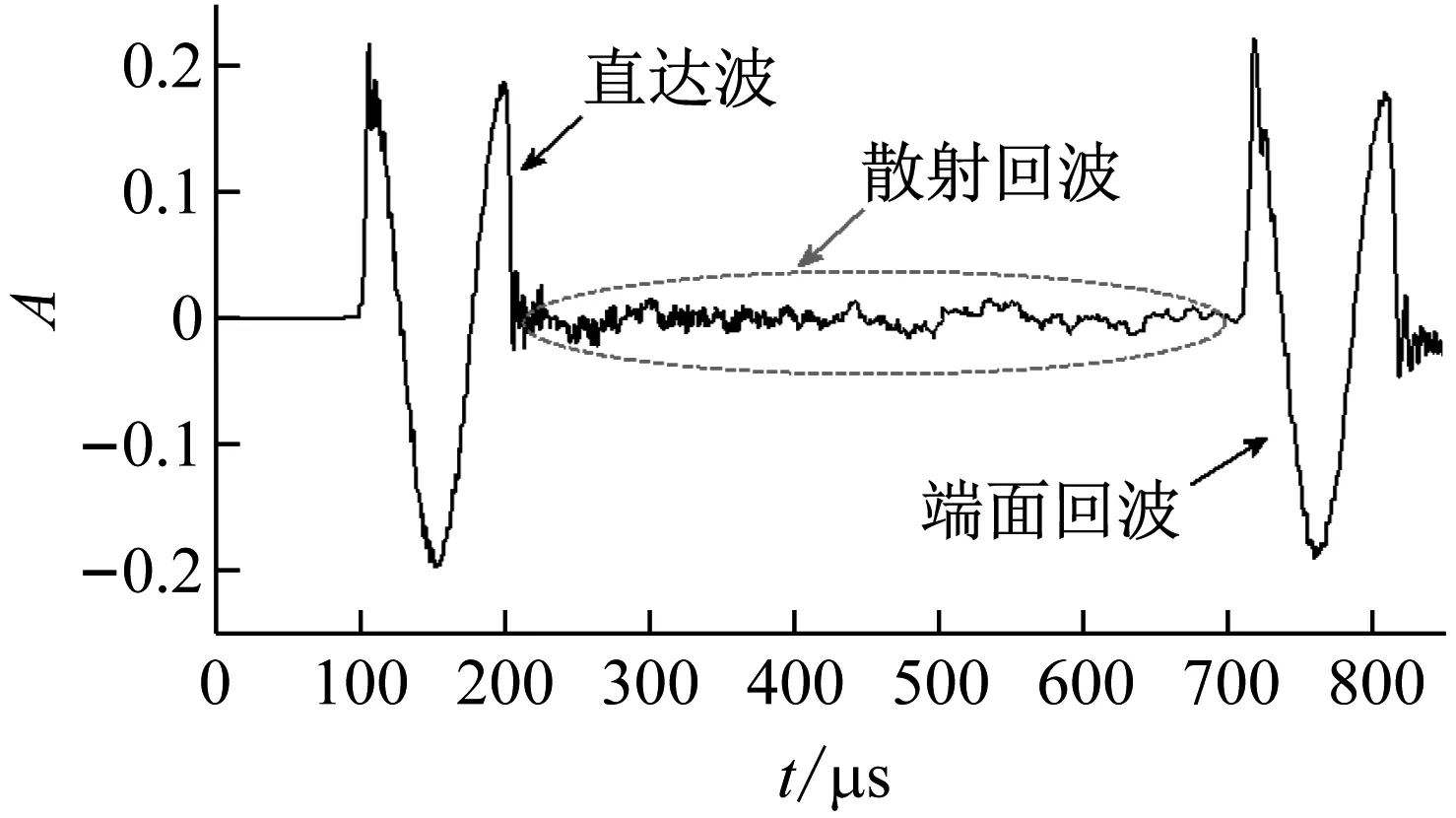
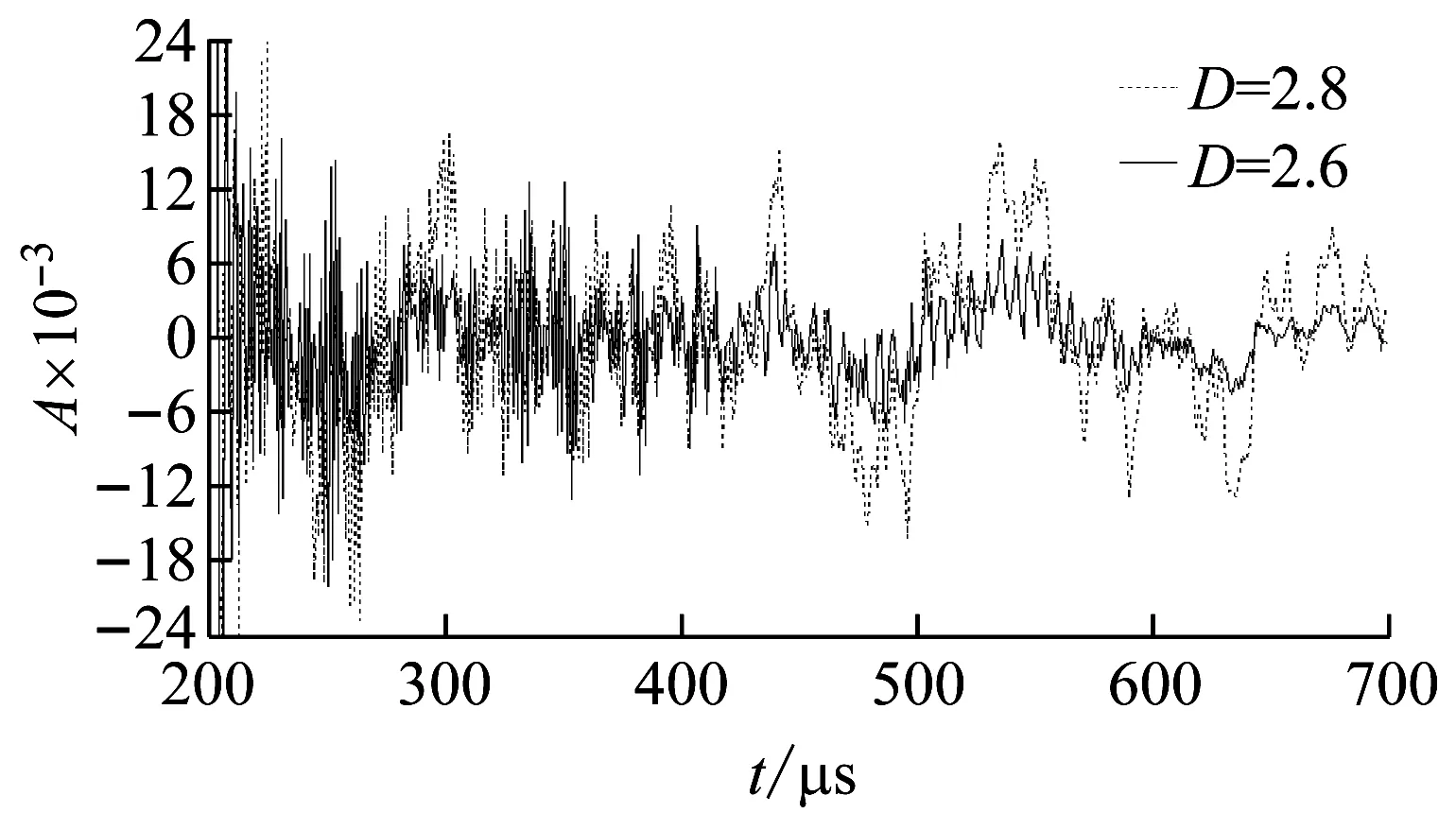
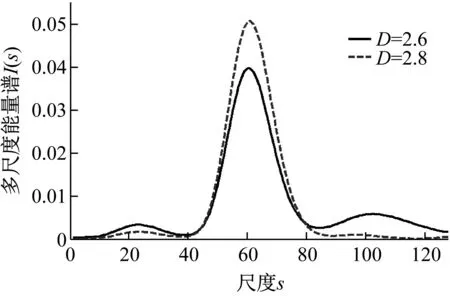
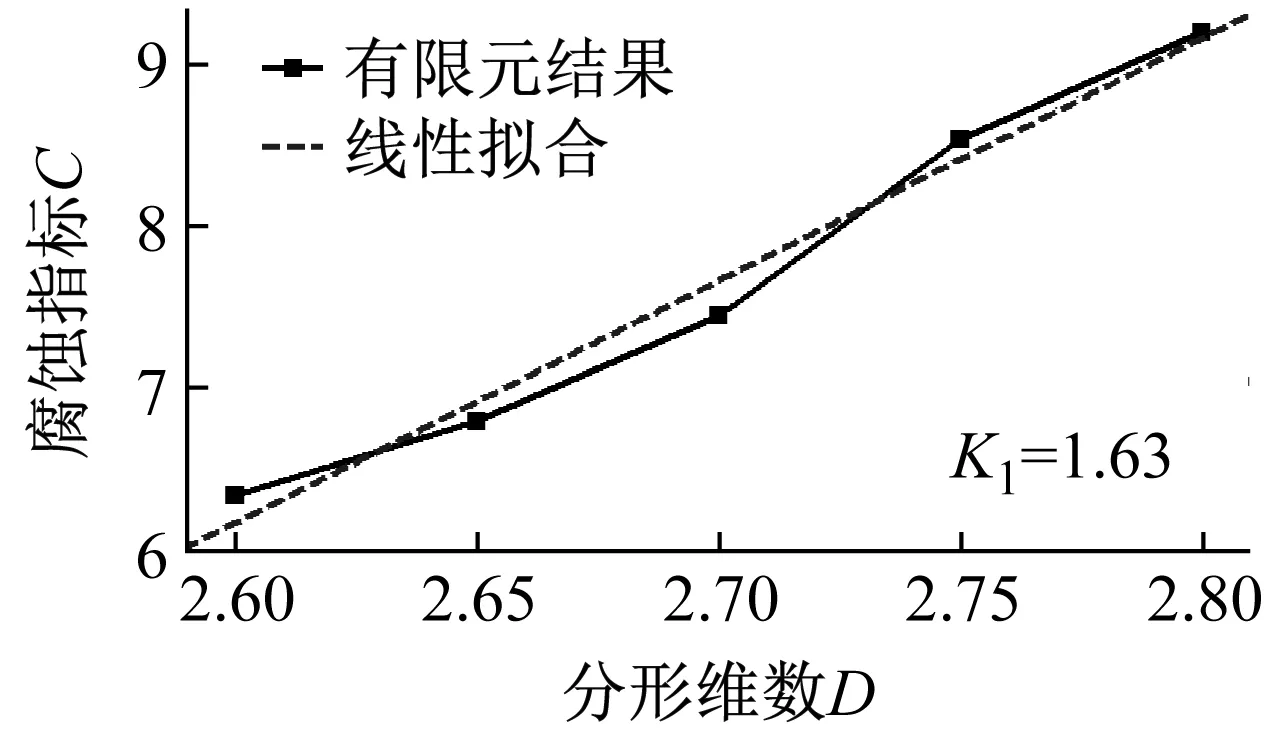
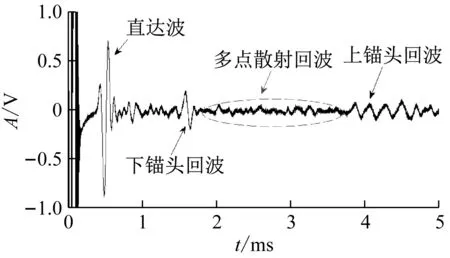
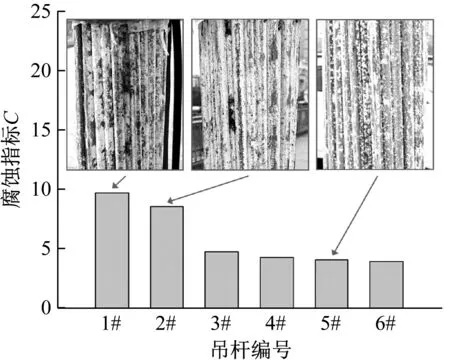
式中:2 由于分形函数要求x≠0,y≠0,采用X=1+x/L,Y=1+y/P,将x,y归一化到[1,2]区间内。其中,L为钢丝长度,P为钢丝横截面周长。对于轴对称模型而言Y为[1,2]区间内的任意值,本文取Y=1.5。 将式(11)求得的钢丝表面展开形貌高度Z(X,Y),转换成沿轴向各个截面半径R,公式为 R(X)=r-max[Z(X,1.5)]+Z(X,1.5) (12) 式中:R(X)为腐蚀后沿轴向各个截面半径;r为未腐蚀钢丝半径。 研究成果表明,分形维数D与钢丝腐蚀表面的腐蚀程度和形貌复杂度密切相关。腐蚀表面形貌越复杂,腐蚀程度越严重,其分形维数越大,且腐蚀钢丝表面分形维数在2.6~2.8。因此,通过改变分形维数的大小,可以得到不同腐蚀程度下的钢丝表面,如图4所示。 图4 不同分形维数下的钢丝表面 通过后处理文件修改有限元模型中轴对称单元节点坐标,得到对应的腐蚀钢丝有限元模型,如图5所示。 图5 腐蚀钢丝有限元模型 采用10 kHz,50 kHz,100 kHz正弦脉冲对杆端整个截面进行垂直激励,激励时长均为100 μs,以激发高强钢丝中不同频率的纵向导波,接收点为距激励端0.5 m处的钢丝中心节点。 当D=2.8时,10 kHz导波时域波形如图6所示。 图6 当D=2.8时10 kHz导波的时域波形 由图6可知,直达波与端面回波的声时差为588 μs,根据接收点距导波反射端面距离,可计算得到导波计算波速v=3 m/588 μs=5 102 m/s,与图1中的理论分析结果相比,仅相差1.1%。直达波与端面回波之前存在明显的多点散射回波,多个缺陷回波相互叠加,难以观察到明显的局部缺陷回波。 不同分形维数下的散射回波,如图7所示。散射回波随分形维数增加变化复杂,仅从时域散射波形无法判断腐蚀程度。 图7 不同分形维数下的多点散射回波 按照式(8),计算多点散射回波的多尺度能量谱I(s),如图8所示。 图8 不同分形维数下的多尺度能量谱 由图8可知: (1) 不同分形维数下,散射回波的多尺度能量谱I(m)主要能量集中在尺度40~80附近,峰值均出现在尺度61处。当分形维数较小时,腐蚀散射较弱,散射回波中包含有一定的噪声信号,使得散射回波的多尺度能量谱在尺度为103和23处出现了明显的第二、第三峰值。 (2) 随着分形维数的增加,多尺度能量峰值显著上升,第二、第三峰值逐渐消失。这是由于导波散射加强,大量直达波信号在腐蚀边缘发生散射,使得散射回波的多尺度能量谱逐渐向部分尺度集中。较高分形维数相比,低分形维数下散射回波的多尺度能量分布更为均匀。 (3) 不同分形维数下,散射回波的多尺度能量谱变化显著,表明采用散射回波的多尺度能量谱作为特征向量可以有效反映腐蚀损伤。但其变化规律难以量化表述,仅从多尺度能量谱的变化无法准确判断腐蚀程度。 导波在传播至腐蚀处时发生散射和透射。随着腐蚀程度的增加,散射增强,透射波能量逐渐降低。端面回波可看做最大腐蚀程度下(截面损失率为100%)的散射回波,此时导波散射最强,透射波能量几乎为0。当以端面回波的多尺度能量谱作为基准向量时,散射回波的多尺度能量谱与基准值之间的差异可以有效反映腐蚀程度。因此,采用相对熵[27]来描述两向量之间的差异程度,并以该值作为判断腐蚀程度的指标。腐蚀指标C的定义为 (13) 式中,Ic,Ir分别为散射回波和端面回波的多尺度能量谱。 根据式(13)计算不同分形维数下的腐蚀指标C如图9所示。从图9可知,K为腐蚀指标随分形维数的变化曲线斜率,反映了腐蚀指标对腐蚀扩展的敏感性。K值越大,腐蚀程度的变化在腐蚀指标C上反映得更为明显。 (a) 10 kHz 比较不同频率导波的腐蚀指标与分形维数的变化规律可知: (1) 不同频率下,腐蚀指标均随分形维数的增加单调上升,指标值变化明显,采用特征向量相对熵作为腐蚀指标可以有效反映腐蚀状态。 (2) 比较不同频率导波腐蚀指标的敏感性系数K1,K2,K3可知,随着导波频率的增加,K值逐渐上升。较10 kHz相比,50 kHz和100 kHz导波分别增加6.13%,131.902%,表明腐蚀指标受频率的影响,频率越高,腐蚀指标对腐蚀程度的分辨率和对腐蚀扩展的敏感性越强。比较K2和K3的增长趋势;当频率越高时,K值的上升趋势明显增加。值得注意的是,高频导波衰减较强,在实桥检测中采用高频导波往往难以观察到端面回波。因此,在实桥检测时,应根据导波衰减情况选择导波频率。 某拱桥建成于1998年,主桥采用三跨连续无风撑下承式钢管混凝土系杆拱结构,跨径组合(55+83.6+55)m。全桥共33对吊杆,吊杆间距为5 m。吊杆均采用镀锌钢丝挤包双护层扭绞型成品索。该桥吊杆服役近22年,已超过设计使用年限,存在较大的安全隐患。 为掌握吊杆内部钢丝损伤情况,采用磁致伸缩导波检测系统对该桥吊杆进行检测。磁致伸缩传感器利用电磁场和铁磁材料的磁致伸缩效应及其逆效应实现导波的激励与接收,检测时无需与被检对象直接接触,因此,将磁致伸缩传感器安装于吊杆表面,对吊杆内部钢丝进行磁化,通过磁场改变激发出吊杆中的纵向导波,其激励效果与有限元保持一致。由于高频导波衰减较强,其实测信号难以观察到端面回波,因此,采用10 kHz的低频纵向导波进行吊杆腐蚀评估,现场传感器布置如图10所示。 图10 传感器布置示意图 随机抽取该桥6根吊杆进行导波检测,典型吊杆检测波形如图11所示。 由图11可知,根据直达波到达时刻和传感器安装间距计算1#吊杆和5#吊杆的实测波速分别为5 122 m/s和5 141 m/s,与理论波速相比,偏差均小于2%。根据实测波速和锚头回波时刻计算吊杆索长分别为12.86 m和14.18 m,与理论索长相比,偏差均小于7.5%。导波检测信号中均未出现明显的局部缺陷回波,仅从实测导波信号,难以识别吊杆腐蚀损伤。 (a) 1#吊杆 上锚头回波传播距离较远,能量衰减较强,回波往往较弱,在长吊杆中甚至难以观察到上锚头回波。因此,本文选取下锚头回波,按照式(13)计算各吊杆实测导波信号的腐蚀指标C,根据腐蚀指标对典型吊杆进行现场开窗验证,如图12所示。 图12 吊杆腐蚀指标及开窗验证 由图12可知: (1) 不同吊杆实测导波的腐蚀指标差异明显,指标值分布在3.91~9.65,1#,2#吊杆腐蚀指标C明显高于其他吊杆。2#~6#吊杆腐蚀指标较小,指标值较为接近,分布在3.91~4.71。 (2) 对腐蚀指标C较大的1#,2#吊杆和腐蚀指标C较小的5#吊杆进行开窗验证,结果表明,1#,2#吊杆索内钢丝均存在明显锈蚀,5#吊杆表面仅有镀锌层锈蚀产物构成的白色晶体析出,索内钢丝未见明显锈蚀,处于腐蚀萌生阶段。腐蚀指标C识别结果与吊杆开窗验证结果一致,腐蚀指标C与吊杆锈蚀程度具有明显的相关性,通过腐蚀指标C可以有效识别吊杆腐蚀状况。 采用导波多点散射特征进行了吊杆腐蚀损伤识别。通过引入分形函数,建立了多点腐蚀钢丝的有限元模型,分析了多点散射回波的多尺能量特征。将携带有腐蚀信息的多尺能量谱作为特征向量构建腐蚀指标,并进行了实桥验证。得到结论如下: (1) 不同腐蚀程度下,多点散射回波的多尺度能量谱变化显著。基于散射回波多尺度能量谱的腐蚀指标随腐蚀程度的增加线性上升,指标值变化明显。采用多尺度能量谱作为特征向量构建腐蚀指标可以有效反映腐蚀损伤。 (2) 随着导波频率的增加,识别指标的损伤敏感性上升。较10 kHz相比,50 kHz和100 kHz的敏感性系数K值分别增加6.13%,131.902%。 (3) 吊杆实测腐蚀指标差异明显,指标值分布在3.91~9.65。吊杆现场开窗检测结果与腐蚀指标识别结果一致,该腐蚀指标可以有效识别出在役拱桥吊杆内部钢丝腐蚀。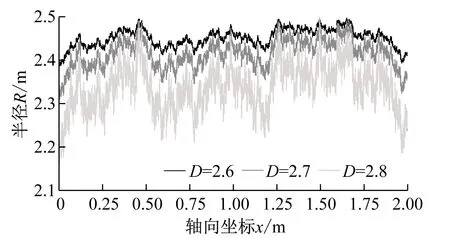
2.2 散射回波的多尺度能量分析
2.3 腐蚀评估指标
3 实桥验证
3.1 工程概况

3.2 检测结果及验证
4 结 语
