基于径向基模型和巴氏距离的随机有限元模型修正

张亚峰， 彭珍瑞， 张雪萍， 董康立

(1.兰州交通大学 机电工程学院，兰州 730070；2.浙江大学 生物医学工程与仪器科学学院，杭州 310027)

当前绝大多数的模型修正法都属于确定性方法，没有考虑结构参数和响应的不确定性，从而降低了其工程实际的应用价值。由于工程问题普遍存在不确定性，如结构材料参数与几何尺寸的不确定性，结构在服役期间的各类装配带来的装配不确定性，试验测试数据的不确定性和噪声等因素的影响，不确定性广泛存在于实际结构的参数和响应中是无法回避的问题[1-2]。随机模型修正法属于不确定性模型修正法，由于真实结构的测量数据是随机的，结构模型的修正参数必须是随机的，基于随机测量数据的结构参数修正过程称为随机模型修正[3]。随机模型修正可以使实测统计数据与预测的随机响应或基本动态特性之间的误差减小，因此，随机模型修正具有重要意义[4-5]。

在模型修正过程中使用代理模型替代有限元模型均可减小计算量，是解决复杂工程结构优化问题的有效途径之一[6]。常见的代理模型主要有多项式响应面模型、径向基函数模型(radial basis function，RBF)、Kriging模型、神经网络模型等[7]。径向基代理模型以其结构简单、预测精度高和能以任意精度逼近任意连续函数的优点，已被广泛应用于土木、航天和机械等领域[8]。近年来，众多学者研究了考虑不确定性的模型修正法，并取得了成果。姚春柱等[9]提出了针对参数不确定性的综合贝叶斯有限元模型修正法。方圣恩等[10]提出了一种随机模型修正法以确定结构不确定性参数的概率统计特性，使得模型修正的应用更符合工程实际。Wan等[11]采用贝叶斯法对参数不确定性进行量化的随机模型修正。陈喆等[12]研究了考虑试验模态参数不确定性的有限元模型修正法。Jalali等[13]利用贝叶斯识别法对连接模型参数中的不确定性进行识别。Bi等[14]通过近似贝叶斯计算模型修正框架，进一步推广了巴氏距离作为一种新的不确定性度量的应用。秦仙蓉等[15]研究了考虑参数不确定性的随机有限元模型修正法能有效修正岸桥结构参数的均值和标准差。Huang等提出了一种基于混合摄动-加勒金的随机模型修正法。Zhao等[16]提出了一种鲁棒性随机模型修正法，更好地估计参数的不确定性。然而，这些方法都是基于模态参数的模型修正法。在基于模态参数的模型修正方法中，实测模态参数的不完备性和模态分析误差可能会对修正后的模型产生显著的影响[17]，与其相比，基于频响函数(frequency response function，FRF)的模型修正方法具有以下优点[18-19]：避免了模态识别过程中的误差；测量数据的不完备性对基于FRF的模型修正法影响较小；FRF中包含的结构数据信息多于模态参数中包含的结构信息；FRF具有互易性，在一点得到的数据可以通过另一点得到验证，因此，这些数据具有更高的可信度。巴氏距离是一种基于离散和连续概率分布的相似性计算方法，它可以对两者的重叠量进行近似计算，以此实现两者的相关性度量。巴氏距离度量可以测量得到不确定性度量的特征，而不会丢失重要信息，且可以同时对所有特征进行度量，实现对多个不确定性特征精细、量化和统一的度量。

综上，结合FRF和巴氏距离的优势，本文提出了基于径向基模型和巴氏距离的随机有限元模型修正法。首先，将加速度FRF通过小波变换，提取第5层低频小波系数作为输出响应特征量来构造径向基模型，并通过土狼优化算法(coyote optimization algorithm，COA)确定径向基模型的方差值。然后，通过花朵授粉算法(flower pollination algorithm,FPA)最小化巴氏距离进行两步(①拉近两个分布的距离，修正参数均值；②根据已修正的参数均值来修正参数标准差)和同步求解待修正参数均值和标准差。最后通过平面桁架结构和空间桁架结构验证了本文所提方法的有效性。

1 小波变换

小波变换通过伸缩平移运算对信号逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，从而可聚焦到信号的任意细节[20]。

对一维信号y(t)的小波变换，给定一个基函数ψ(t)，令

(1)

式中:a为伸缩因子；b为尺度因子。为计算方便，在实际分析和应用中，需将连续小波及小波系数进行离散化处理，则y(t)的小波变换为

t=1,2,…,n

(2)

式中,WTy(a,b)为y(t)的小波系数。对比多次试验效果，本文中设定基函数为db3，分解层数为5层。对加速度FRF进行小波分解，提取第5层低频小波系数作为构造径向基模型的输出，也作为加速度频响函数的响应特征量进行模型修正。

2 径向基模型的构造

2.1 径向基神经网络的基本原理

在d维设计空间中生成一组数量为k的初始样本点x1,x2,…,xk∈Rd，目标的真实响应值为y(x1),y(x2),…,y(xk)，径向基插值函数的数学形式为：

(3)

由s(xi)=y(xi)，可得：Φ·W=Y，即W=Φ-1×Y，式中，W=[w1,w2,…,wi]T为权系数向量，Y=[y(x1),y(x2),…,y(xk)]T

(4)

选用应用较广的高斯插值基函数，表达式为

(5)

2.2 土狼优化算法(COA)

COA是由Pierezan等[21]提出的用于全局优化的自然启发的元启发式算法。COA包括随机初始化土狼群、随机分组、土狼生死和被组驱离与接纳等过程。

(1) 随机初始化土狼群。将全体土狼分为Np个组，每组中有Nc只，参数维数为D，参数上下界为lb和ub。如式(6)所示

socj=lbj+rj(ubj-lbj)

(6)

式中,rj为[0,1]内的随机数，j=1,2,…,D。评估每个土狼的社会适应能力并随机分组。

(2) 寻找组内最优的alpha狼，并联系所有土狼的信息，计算群体的文化趋势。

(3) 组内的文化互动，即土狼受到alpha狼影响(δ1)和群体影响(δ2)。

(4) 更新土狼的社会条件，如式(7)所示

new_soc=soc+r1×δ1+r2×δ2

(7)

式中,r1和r2为[0,1]中的随机数。使用贪心算法优胜劣汰，保留最优土狼。

(5) 考虑生命中主要两个事件，即出生和死亡。新土狼的诞生是由随机选择双亲的遗传因子和环境影响共同作用的结果，例如

(8)

ps=1/D,pa=(1-ps)/2

(9)

幼崽在出生之前就有10%的死亡率，且土狼的年龄越大死亡的机率就越大。

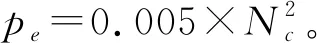
2.3 径向基模型构造及验证

建立一个严格径向基模型，需要先设定一个方差值σ2，方差值直接影响径向基模型的预测精度。采用拉丁超立方抽样方法抽取初始待修正参数±20%区间内的样本，将其分为训练集和测试集(训练集和测试集数据互不相同)，并计算相应的响应特征量。建立目标函数

(10)

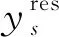
(11)

3 巴氏距离

巴氏距离在信号处理、特征提取和模式识别等方面得到了广泛的应用。巴氏距离用来度量两个概率分布之间的相似性。

在连续域Y上的概率密度分布函数为P(y)和Q(y)，巴氏系数定义为

(12)

式中,0≤ρ≤1。巴氏距离的定义为

BD(P,Q)=-lnρ

(13)

式中,0≤BD(P,Q)≤∞，对于离散域，离散巴氏距离重新定义为

(14)

由式(12)和式(13)可知，若两个分布没有重叠，巴氏系数将会等于0或趋于0，则巴氏距离为无穷大，反之，若两个分布相同，巴氏系数将会等于1或趋于1，则巴氏距离为0或趋于0，因此，巴氏距离的大小取决于巴氏系数。巴氏距离越小，表示两个概率分布越相似。

对于多变量高斯分布P=N(mP,θP)和Q=N(mQ,θQ)，巴氏距离具体公式为

(15)

式中,θ=(θP+θQ)/2。

4 模型修正过程

利用FPA进行随机有限元模型修正。FPA具有异花授粉(全局寻优)和自花授粉(局部寻优)两大特性。异花授粉过程可以逃离任何局部景观，进而探索更大的空间；自花授粉过程使相似的解被更频繁地选择，从而保证更快地收敛，其收敛速度本质上是指数，因此寻优效率更高，性能优于遗传算法和粒子群算法[22]。

(1) 两步修正参数均值和标准差。第一步拉近两个分布的距离，因此，运用FPA先修正参数均值，构造如下目标函数

(16)

第二步根据已修正的均值，产生服从高斯分布的2 000个随机样本，通过已构造的径向基模型预测随机样本响应特征量，运用FPA以最小化巴氏距离为目标函数修正参数标准差。值得说明，每次迭代过程中，都需根据已修正的均值来重新产生服从高斯分布的2 000个随机样本参与有限元模型修正。模型修正流程如图1所示。

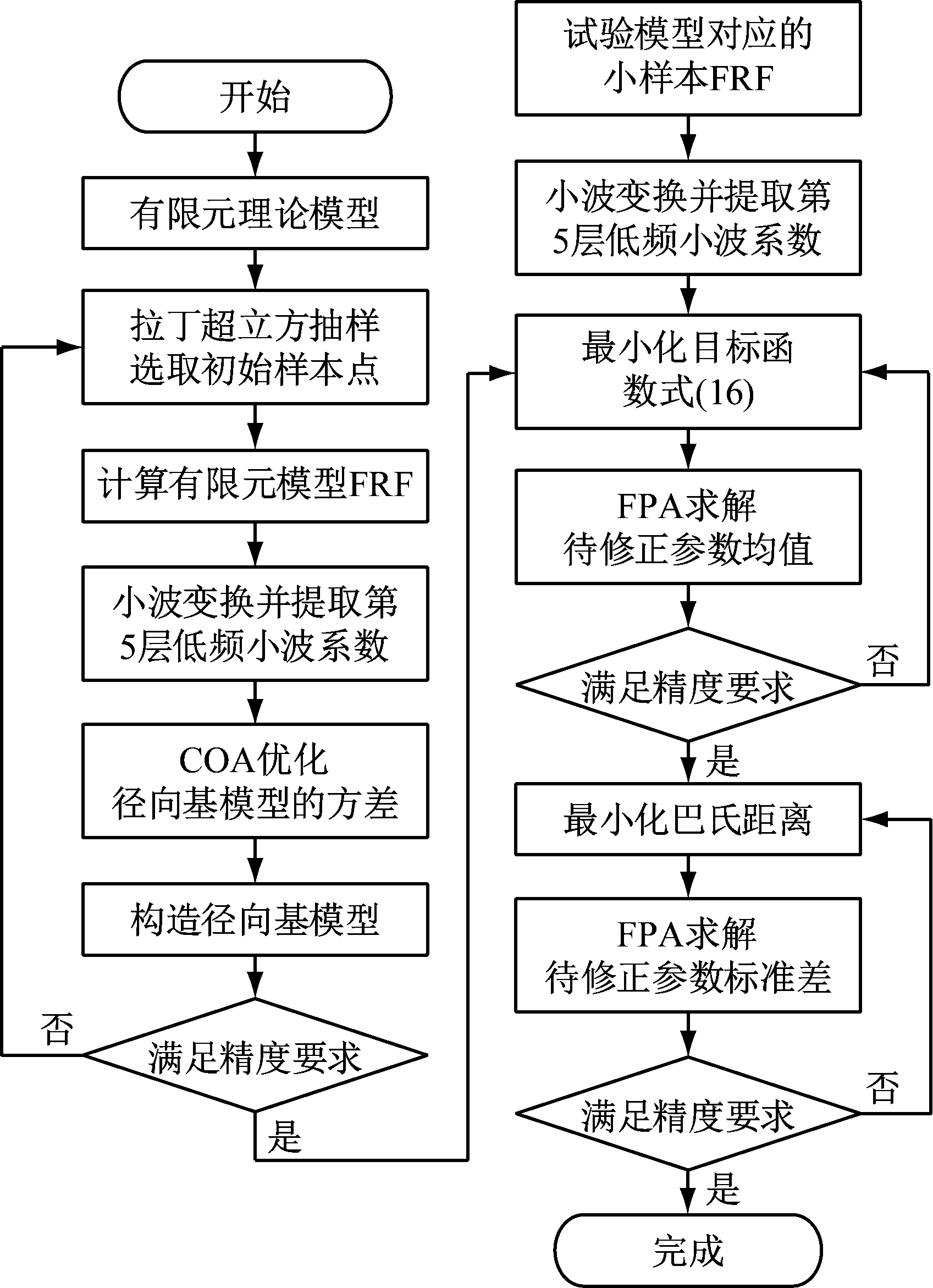
图1 模型修正流程图

(2) 同步修正参数均值和标准差。随机抽取服从高斯分布的2 000个随机样本，通过已构造的径向基模型预测随机样本响应特征量，运用FPA直接以巴氏距离为目标函数同时求解待修正参数均值和标准差。值得说明，每次迭代过程中，同样重新产生服从高斯分布的2 000个随机样本参与有限元模型修正。

5 数值算例

5.1 平面桁架

平面桁架结构，如图2所示。该桁架模型由36个杆单元组成，共有16个节点和29个自由度，单元横截面积为1 cm2，箭头为激励位置，⊗为测点位置。选择结构弹性模量(E)和材料密度(d)的均值及标准差作为模型待修正参数。初始有限元模型E和d的均值分别为231 GPa和7 020 kg/m3，试验模型E和d的均值分别为210 GPa和7 800 kg/m3，标准差分别为2.2和25。初始有限元模型E与d的均值和试验模型E与d的均值的相对误差分别为10%和-10%。

图2 平面二维桁架结构

采用拉丁超立方抽样方法抽取550组样本，选取前450组作为训练集，后100组作为测试集。采用2.3节方法构造径向基模型，得到径向基模型的方差值为0.108 4，迭代情况如图3所示。然后根据式(11)计算得到RMSE为3.74×10-5。为了进一步评估径向基模型的预测精度，测试集样本第11响应特征量和第16响应特征量的有限元模型值和径向基模型预测值的重合如图4所示。从图4可知，径向基模型预测值和有限元值几乎全部重合，说明所建立的径向基模型预测精度很高，可以替代有限元模型。

图3 COA迭代曲线

图4 测试集样本的预测值和真实值

以试验模型参数均值和标准差随机抽取服从高斯分布的200个样本进行计算有限元模型加速度FRF，通过小波变换提取第5层低频小波系数作为仿真试验响应特征量。值得说明，在实际应用中很难得到大样本试验数据，因此可以使用半试验样本数据。两步修正：根据式(16)，计算仿真试验响应特征量的均值，并通过FPA迭代修正参数均值。然后，依据已修正均值，修正标准差，参数修正后的结果如表1所示。

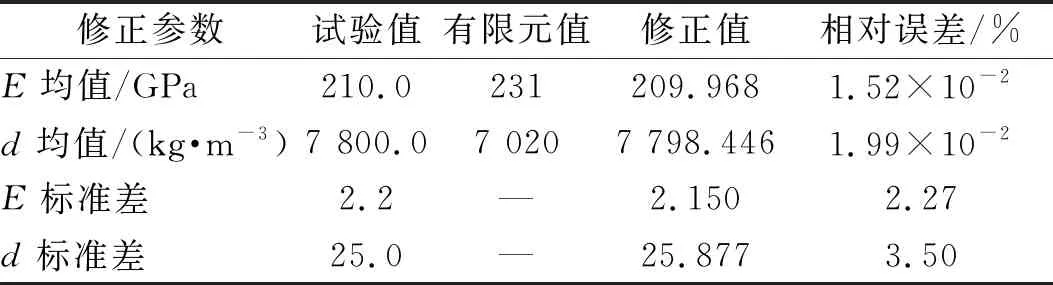
表1 平面桁架结构修正前后结构参数均值与标准差

由表1可以看出，对结构参数均值修正的相对误差值很小，且对结构参数标准差修正的相对误差小于4%，表明本文所提两步进行随机模型修正取得了很好的效果。为进一步验证修正效果，使用表1中修正后的结构参数均值计算修正后的有限元模型加速度频响函数均值(称为径向基模型加速度频响函数)。图5给出了初始有限元模型、试验模型和径向基模型的加速度频响函数均值曲线，从图5可以看出，修正后的有限元模型和试验模型的加速度频响函数均值曲线基本重合。然后以修正后的结构参数均值和标准差随机抽取服从高斯分布的200个样本计算修正后的有限元模型响应特征量的概率密度函数。图6给出了修正后的有限元模型和试验模型的第12和第16响应特征量分布云图及相应95%的置信椭圆，从图6可看出，修正后的有限元模型和试验模型的置信椭圆大小(反映标准差大小的差异)基本一致。图7和图8分别给出了修正后的有限元模型和试验模型的第13和第17响应特征量的概率密度函数，从图7和图8可以看出，修正后的有限元模型和试验模型的概率密度函数曲线充分接近。

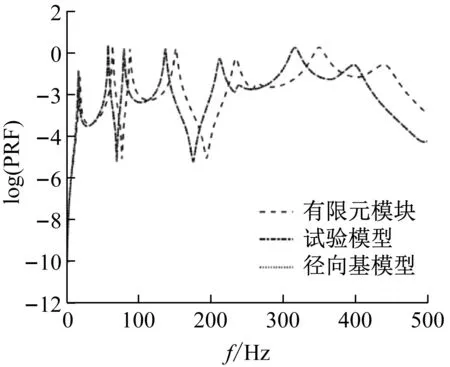
图5 频响函数曲线

图6 分布云图及置信椭圆

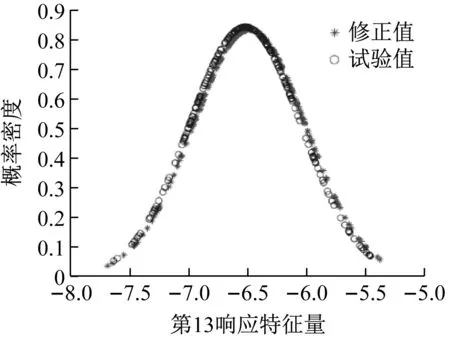
图7 重合度分布图

图8 重合度分布图

同步修正：使用与两步修正相同的试验数据来同时求解参数均值和标准差。修正迭代情况如图9所示。修正结果如表2所示。

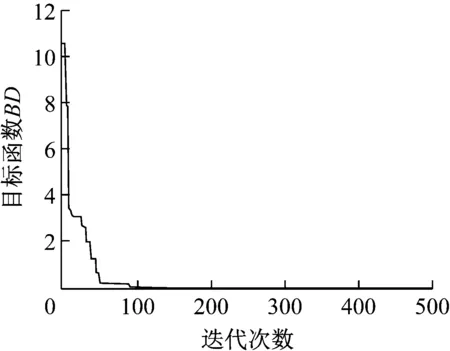
图9 花朵授粉算法同时修正均值标准差迭代曲线

由表2可知，同步修正参数均值和标准差的相对误差值很小，与两步修正具有同样的效果，而在时间上相比两步修正节省了许多。同样，以表2修正后的参数均值和标准差随机抽取服从高斯分布的200个样本计算修正后的有限元模型响应特征量的概率密度函数。图10给出了修正后的有限元模型和试验模型的第12和第16响应特征量分布云图及相应95%的置信椭圆，从图10可看出，修正后的有限元模型和试验模型的置信椭圆大小基本一致。图11和图12分别给出了修正后的有限元模型和试验模型的第13和第17响应特征量的概率密度函数，从图11和图12可以看出，修正后的有限元模型和试验模型的概率密度函数曲线充分接近。综上，验证了本文所提同步随机模型修正的有效性。

表2 平面桁架结构修正前后结构参数均值与标准差

5.2 空间桁架

空间桁架结构,如图13所示。该桁架模型由72个杆单元组成，共有20个节点和48个自由度，单元横截面积为1 cm2，箭头表示激励位置和⊗表示测点位置。选择结构弹性模量(E)和材料密度(d)的均值及标准差为模型待修正参数。初始有限元模型E和d的均值分别为209 GPa和7 020 kg/m3，试验模型E和d的均值分别为190 GPa和7 800 kg/m3，标准差分别为2和25。初始有限元模型E与d的均值和试验模型E与d的均值的相对误差分别为10%和-10%。

图13 空间三维桁架结构

采用拉丁超立方抽样方法抽取600组样本，选取前500组作为训练集，后100组作为测试集。采用2.3节所述方法建立径向基模型，得到径向基模型的方差值为0.101 3。根据式(11)计算得到RMSE为9.29×10-5。为了进一步评估径向基模型的预测精度，测试集样本第7响应特征量和第15响应特征量的有限元模型值和径向基模型预测值的重合图,如图14所示。从图14可知，径向基模型预测值和有限元值几乎全部重合，同样说明所建立的径向基模型预精度很高，可以替代有限元模型。

以试验模型参数均值和标准差随机抽取服从高斯分布的200个样本进行计算有限元模型加速度FRF，通过小波变换并提取第5层低频小波系数作为仿真试验响应特征量。两步修正：根据式(16)计算仿真试验响应特征量的均值，通过FPA迭代寻优，修正参数均值，迭代情况如图15所示。然后，依据已修正均值来修正标准差，迭代情况如图16所示。参数修正后的结果如表3所示。

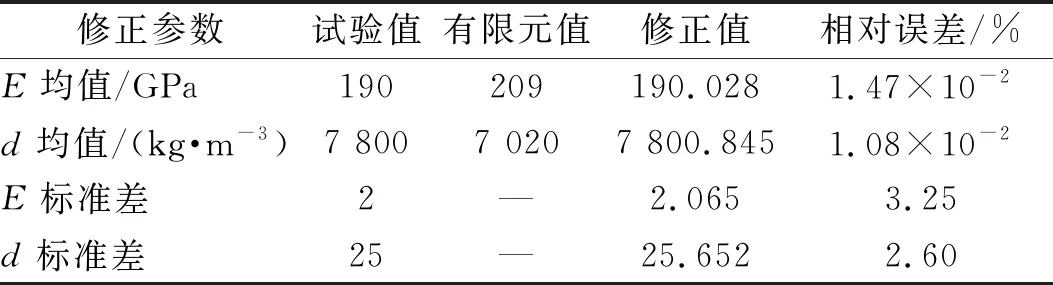
表3 空间桁架结构修正前后结构参数均值与标准差

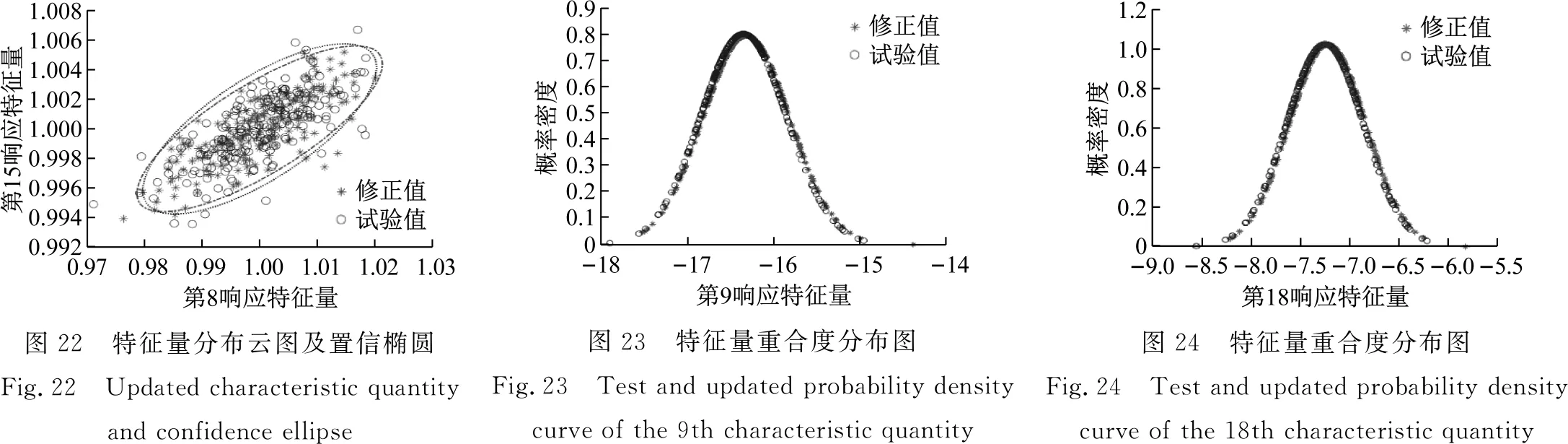
由表3可知，对参数均值修正的相对误差值很小，且对标准差修正的相对误差小于4%，表明本文所提方法进行随机模型修正取得了很好的效果。为了进一步验证修正效果，图17给出了初始有限元模型、试验模型和径向基模型的加速度频响函数均值曲线，从图17可以看出，修正后的有限元模型和试验模型的加速度频响函数均值曲线基本重合。然后以修正后的结构参数均值和标准差抽取服从高斯分布的200个样本计算修正后的有限元模型响应特征量的概率密度函数。图18给出了修正后的有限元模型和试验模型的第8和第15响应特征量分布云图及相应95%的置信椭圆，从图18可以看出，修正后的有限元模型和试验模型的置信椭圆大小基本一致。图19和图20分别给出了修正后的有限元模型和试验模型的第9和第18响应特征量的概率密度函数，从图19和图20可以看出，修正后的有限元模型和试验模型的概率密度函数曲线充分接近。

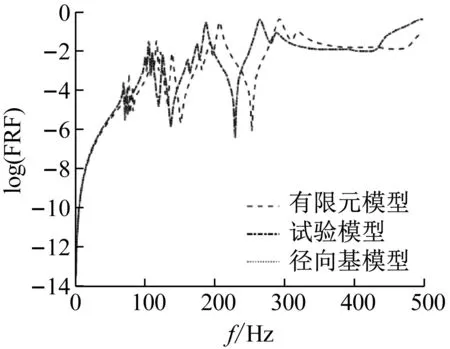
图17 频响函数

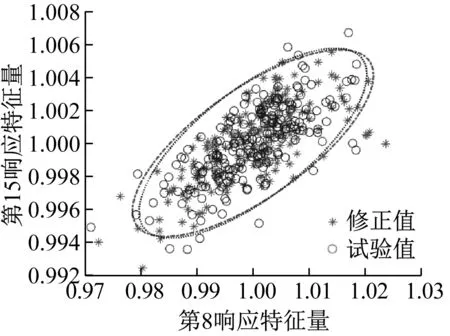
图18 特征量分布云图及置信椭圆

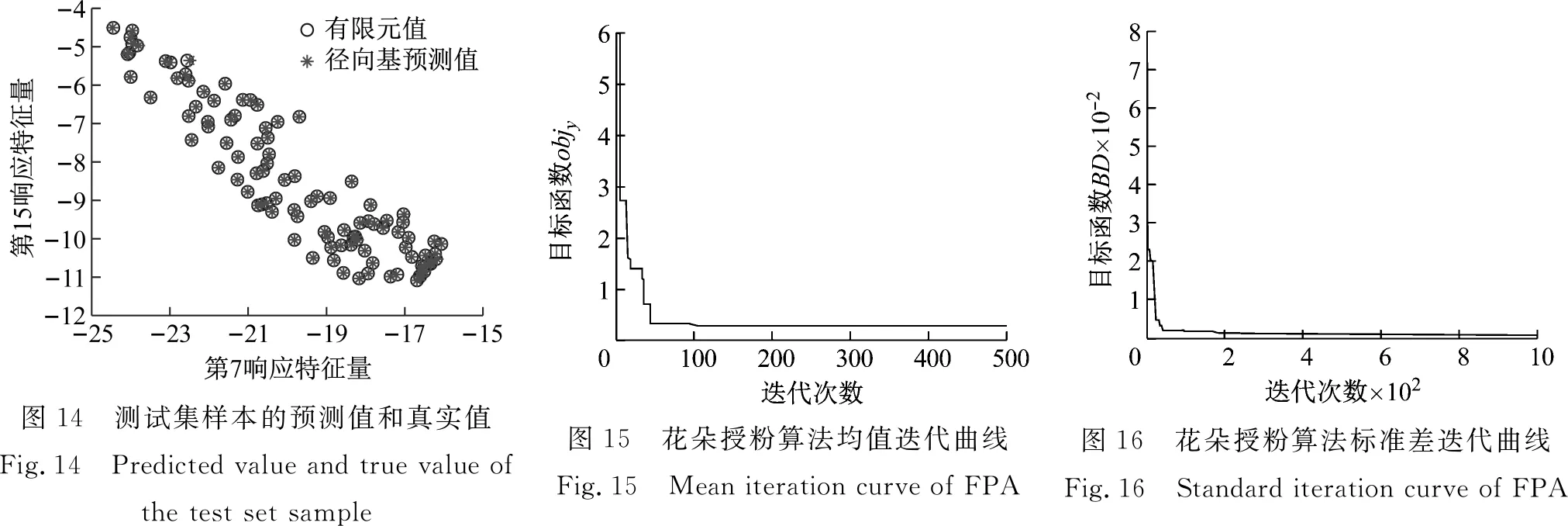
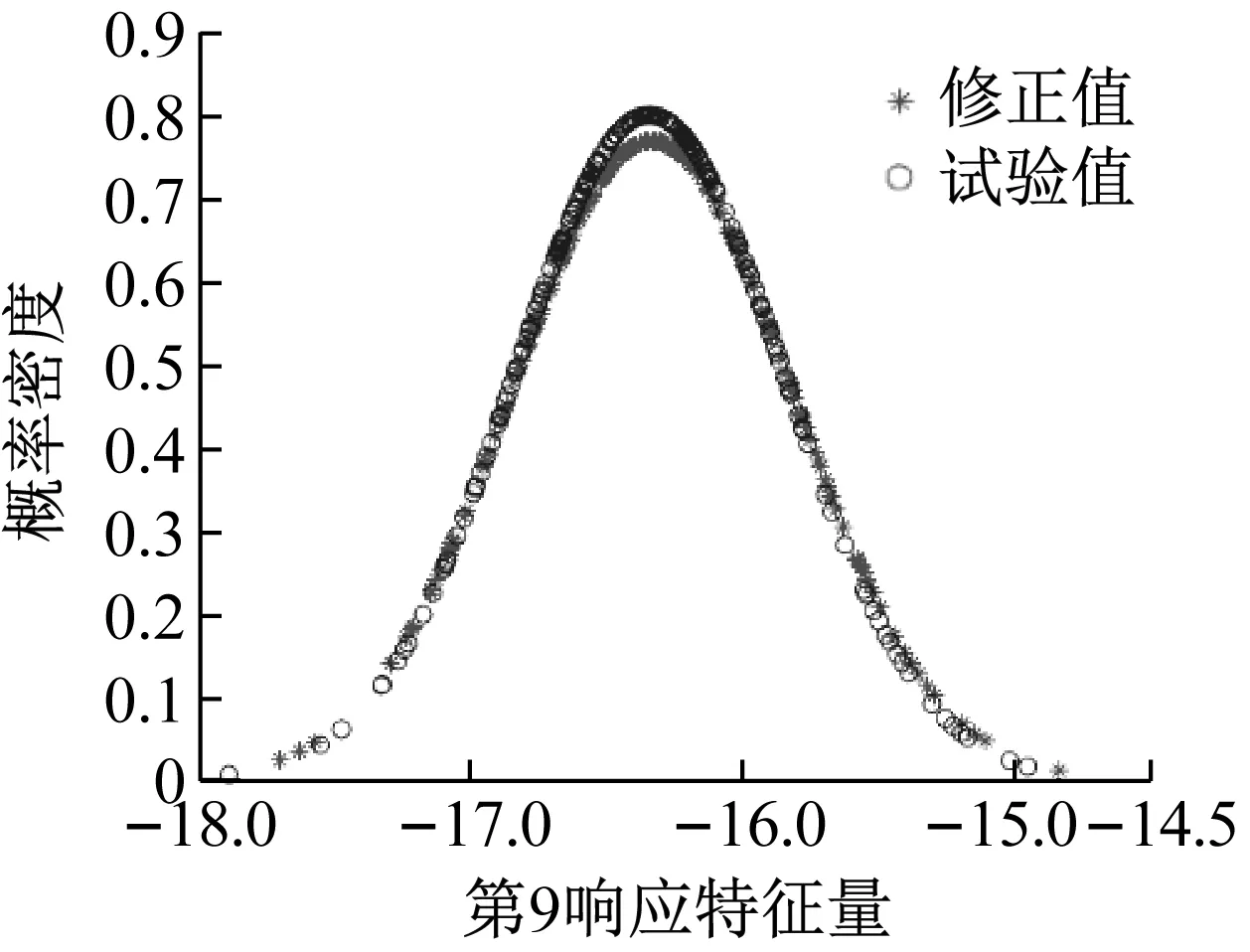
图19 特征量重合度分布图

图20 特征量重合度分布图

同步修正：使用与两步修正相同的试验数据同时求解参数均值和标准差。修正迭代情况如图21所示。修正结果如表4所示。

由表4可知，同步修正参数均值和标准差的相对误差值很小，与两步修正具有同样的效果。由图15、图16与图21相比可知，同步修正参数均值标准差迭代200次之前就已收敛，而两步修正第二步修正参数标准差迭代收敛需要500次以上，因此，在时间上同步修正相比两步修正节省了许多。同样，以表4中修正后的结构参数均值和标准差随机抽取服从高斯分布的200个样本计算修正后的有限元模型响应特征量的概率密度函数。图22给出了修正后的有限元模型和试验模型的第8和第15响应特征量分布云图及相应95%的置信椭圆，从图22可看出，修正后有限元模型和试验模型的置信椭圆大小基本一致。图23和图24分别给出了修正后的有限元模型和试验模型的第9和第18响应特征量的概率密度函数，从图23和图24可以看出，修正后的有限元模型和试验模型的概率密度函数曲线充分接近。综上，验证了本文所提同步修正进行随机有限元模型修正的有效性。

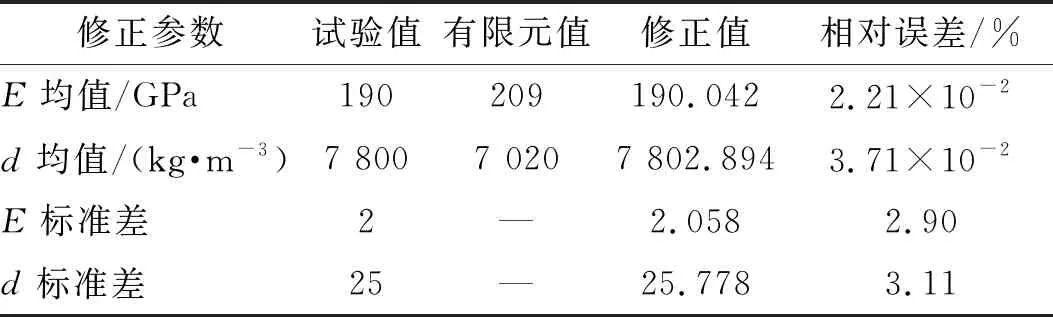
表4 空间桁架结构修正前后结构参数均值与标准差

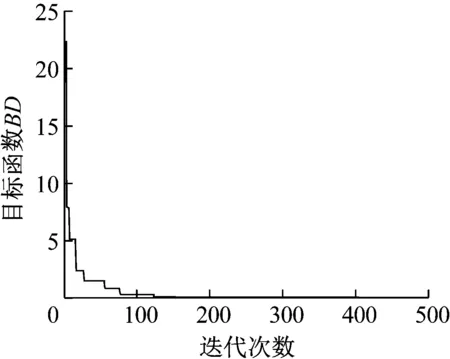
图21 花朵授粉算法同时修正均值标准差迭代曲线

进一步验证同步修正的有效性。初始有限元模型E和d的均值分别为209 GPa和7 020 kg/m3，试验模型E和d的均值分别为180 GPa和7 900 kg/m3，标准差分别为1.8和40。初始有限元模型E与d的均值和试验模型E与d的均值的相对误差分别为16.111%和-11.139%。以试验模型参数均值和标准差随机抽取服从高斯分布的200个样本得到第5层低频小波系数作为仿真试验响应特征量。同时求解参数均值和标准差，修正结果如表5所示。

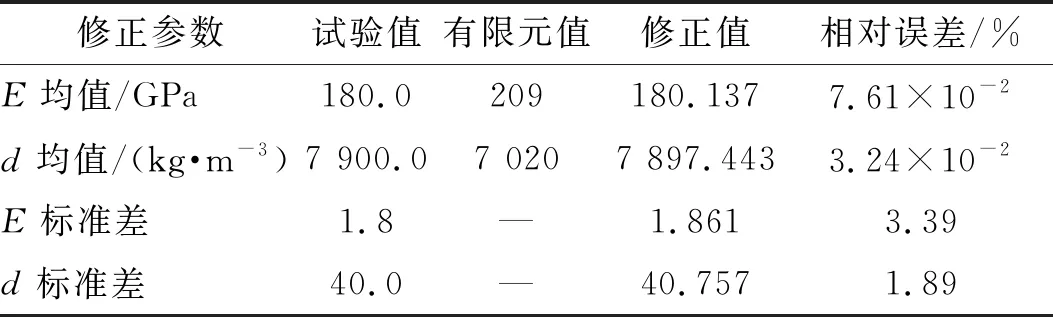
表5 空间桁架结构修正前后结构参数均值与标准差

图25给出了修正后模型和试验模型的第8响应特征量和第15响应特征量分布云图和相应95%的置信椭圆。从图25可知，修正后的有限元模型和试验模型的置信椭圆大小基本一致。第18响应特征量的概率密度函数，如图26所示。从图26可知，修正后的有限元模型和试验模型的概率密度函数曲线充分接近。综上，表明本文所提同步修正在不同的试验响应下的修正具有鲁棒性。同样两步修正也具有此鲁棒性。

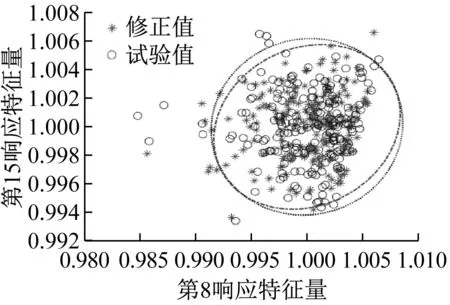
图25 特征量分布云图及置信椭圆

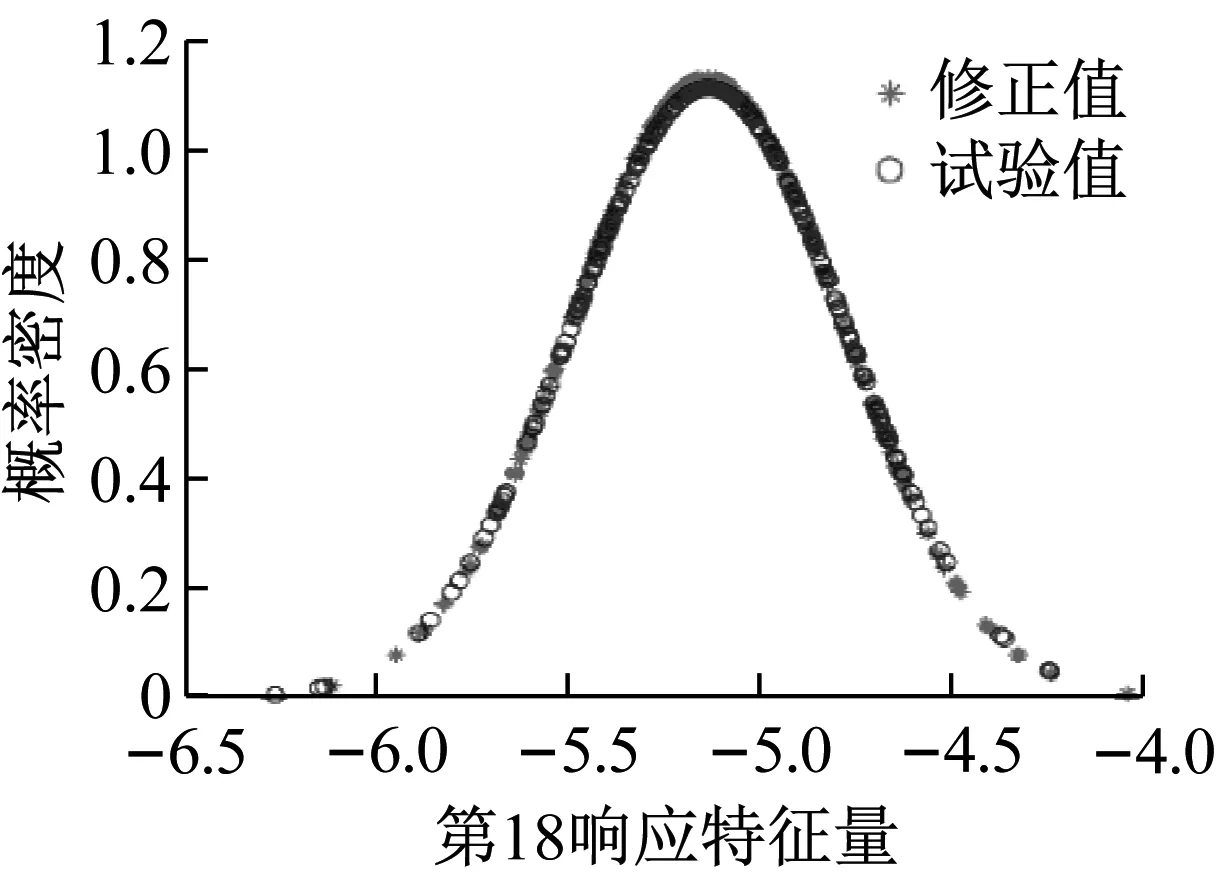
图26 特征量重合度分布图

6 结 论

(1) 考虑参数随机不确定对结构响应分布的影响和巴氏距离在不确定性度量的优势，为此，本文提出以参数均值和标准差为修正目标的两步和同步的随机模型修正方法，修正效果都较好。两个算例表明，两步和同步修正皆可以较好地修正参数的均值和标准差，且在不同的试验响应下对参数均值标准差的修正具有鲁棒性，具有较大的工程应用潜力。

(2) 由于两步修正需要两步迭代求解参数的均值和标准差，且在第二步求解参数标准差的迭代收敛速度就已慢于同步修正求解参数均值标准差的迭代收敛速度，因此，虽然两步和同步修正都可以达到相同的效果，但在时间上同步修正相比两步修正节省了许多。

(3) 在使用参数样本参与不确定性模型修正时构造了径向基模型，并采用优化算法确定径向基模型的方差值，使所构造的径向基模型具有良好的拟合精度和预测能力，能代替有限元模型进行迭代计算，提高模型修正效率。

(4) 将频响函数经过小波变换，提取第5层低频小波系数作为随机模型修正响应特征量，具有保留频响函数特性的优点，且可大量减少输出响应数目，提高了模型修正计算效率。