三维层状黏弹性半空间中球面SH、P和SV波源自由场

巴振宁， 梁建文， 张艳菊

1 天津大学土木系， 天津　300072 2 滨海土木工程结构与安全教育部重点实验室， 天津　300072



三维层状黏弹性半空间中球面SH、P和SV波源自由场

巴振宁1,2， 梁建文1,2， 张艳菊1

1 天津大学土木系， 天津300072 2 滨海土木工程结构与安全教育部重点实验室， 天津300072

摘要采用刚度矩阵方法结合Hankel积分变换，求解了层状黏弹性半空间中球面SH、P和SV波的自由波场.首先，在柱坐标系下建立层状黏弹性半空间的反轴对称(柱面SH波)和轴对称(柱面P-SV波)情况精确动力刚度矩阵.进而由Hankel变换将空间域内的球面波展开为波数域内柱面波的叠加，然后将球面波源所在层的上下端面固定，求得固定层内的动力响应和固定端面反力，将固端反力反向施加到层状黏弹性半空间上，采用直接刚度法求得固端反力的动力响应，叠加固定层内和固端反力动力响应，求得波数域内球面波源动力响应.最后由Hankel积分逆变换求得频率-空间域内球面波源自由场，时域结果由傅里叶逆变换求得.文中验证了方法的正确性，并以均匀半空间和基岩上单一土层中球面SH、P和SV波为例分别在频域和时域内进行了数值计算分析.研究表明基岩上单一土层中球面波自由场与均匀半空间情况有着本质差异；基岩上单一土层中球面波位移频谱峰值频率与场地固有频率相对应，基岩面的存在使得基岩上单一土层地表点的位移时程非常复杂，振动持续时间明显增长；阻尼的增大显著降低了动力响应的峰值，同时也显著减少了波在土层的往复次数.

关键词球面波源； 自由场； 直接刚度法； 层状黏弹性半空间； Hankel变换

The method of direct stiffness combining with the technique of Hankel transform is used to calculate the wave propagation of spherical sources. Firstly, the exact dynamic stiffness matrices of the layered visco-elastic half-space corresponding to the anti-symmetric cylindrical SH-waves and to the symmetric cylindrical P- and SV-waves are established, respectively. Then, the spherical sources expressed in the space domain are expanded as the summation of cylindrical waves in the wave-number domain. The layer in which the spherical sources locate is fixed at its top and bottom interfaces and the dynamic responses restricted in the fixed layer and the corresponding reaction forces are obtained. The directions of these forces are then reversed, and they are applied as loads on the whole layered visco-elastic half-space. The dynamic responses induced by the reactions forces can be determined by using the direct stiffness method. And the dynamic responses restricted in the fixed layer are added to the dynamic responses of the reaction forces to determine the global responses in the wave-number domain. Finally, the free-field responses are obtained by using the inverse Hankel transform. And results in time domain can be easily obtained by using the inverse Fourier transform.

The accuracy of the new method is verified by comparing results with those obtained by Lamb′s method. And by taking spherical SH-, P- and SV-wave sources embedded in a uniform half-space and in a single layered overlying on bedrock as examples, the following numerical calculations are performed. (1) Dynamic responses for different stiffness ratio between the bedrock and the layer are illustrated, and numerical results show that both the real and imaginary parts of the displacement and shear stress have kinks at the interface between the layer and the underlying half-space. (2) Spectrums of surface displacement amplitudes for different layer′s thickness are given, and numerical results show that the spectrums for the single layered half-space have definite peak frequencies, which vary with thickness of the layer. In addition, the dynamic responses of the spherical SH- and SV-wave sources are less sensitive to the layer′s thickness. (3) Effects of material damping ratio on the free field responses are studied, and numerical results show that both the real and imaginary parts of the dynamic responses are decreased significantly with the increase of the material damping ratio, especially for peak displacement and stress. (4) Time domain results are illustrated by using the inverse Fourier transform, and numerical results show that only reflected SH-waves are observed for spherical SH sources, and both the reflected P- and SV-waves can be observed for P- or SV- sources due to Wave Mode Conversion. Additionally, in cases of the single layer half-space, reflected waves from the surface of the bedrock can be observed in the time histories.

The free-field responses for the single layer half-space can be significantly different from those of the uniform half-space case; The peak frequencies of the surface displacement amplitude are strongly related to the fundamental frequencies of the single layer site; The existence of the bedrock makes the time histories of the surface displacement amplitudes very complicated and the duration of vibration very long; And the peak values of the dynamic responses decreased greatly and the times of wave propagating up and down in the layer reduced greatly with the increase of the material damping.

1引言

场地自由场地震反应是研究地震波散射以及土-结构地震相互作用等问题的基础和前提，因此针对场地自由场地震反应的求解和分析有着重要的意义.目前场地自由场地震反应的研究主要是针对平面波进行的，且平面波的研究又包括一维自由场反应和二维自由场反应.一维自由场研究方面：Idriss和Seed(1968)提出了土层地震反应的等效线性化方法，并编制了计算场地一维自由场反应的计算程序SHAKE，此后也对层状场地的一维自由场地震反应进行了研究(高玉峰等, 1999; 金星等, 2004; 栾茂田和林皋, 1992; 李小军, 1987).

对于二维自由场地震反应，Thomson(1950)和Haskell(1953)开创性地给出了层状场地中波传播问题的传递矩阵方法，研究了层状半空间中波的传播问题；Kausel和Roёsset(1981)利用Thomson-Haskell传递矩阵方法给出了层状半空间的刚度矩阵，采用刚度矩阵方法对波的传播问题进行了研究；Wolf和Obernhuber(1982a, 1982b)建立了层状半空间的平面外(平面SH波)和平面内(平面P-SV波)精确动力刚度矩阵，并采用刚度矩阵方法求解了层状半空间中SH、Love、P、SV和Rayleigh波的自由场；薛松涛等(2000,2004)在Wolf理论的基础上，建立层状TI介质的平面外和平面内刚度矩阵，求解了SH、P和SV波入射下层状TI半空间的自由场.刘晶波和王艳(2006)将波动输入转化为等效节点荷载施加在边界节点上，采用有限元法求解了SH波斜入射下弹性半空间的自由场.李山有等(2003)基于水平成层介质波动传播的特点建立了相邻节点间自由场运动的关系式，给出了计算水平成层半空间自由场的时域方程.梁建文等(2014)考虑波型转换，提出了一种层状弹性场地基岩斜入射地震动二维反演方法.Lin等(2005)求解了无黏性饱和半空间中入射P1和SV波的自由场，且考虑了自由表面透水和不透水两种情况.Liang和You(2004)将Wolf理论拓展到层状饱和半空间情况，建立了饱和土层和半空间的平面内精确动力刚度矩阵，并采用刚度矩阵方法求解了层状饱和半空间P1和SV入射下的自由波场.

值得指出的是以上关于地震波自由场的研究均假定入射波为平面波，这在震源距较大时是合适的.当震源距较小时，地震波传播的曲率影响将不能忽略，采用球面波来模拟地震波更为合理.然而目前关于球面波自由场的研究非常少，Lamb(1904)采用Hankel积分变换方法给出了均匀弹性半空间中球面膨胀波源(P波)自由场的计算公式，但没有给出数值结果，对于层状半空间中球面波源自由场，则未见报道.因此本文基于柱面SH、P和SV波势函数，建立了层状黏弹性半空间的反轴对称(柱面SH波)和轴对称(柱面P-SV波)精确动力刚度矩阵，进而采用刚度矩阵方法结合Hankel积分变换求解了层状黏弹性半空间中球面SH、P和SV波源的自由场.

本文关于层状黏弹性半空间中球面波源自由场的研究为今后将震源模拟为点震源，研究复杂场地(盆地、山脉和盆山复合)对地震波的散射以及土结构相互作用等问题提供了精确的自由场波场，另外本文层状黏弹性半空间中球面波的自由波场亦为层状黏半空间中球面波的格林函数，而层状黏半空间中球面SH、P和SV波格林函数构成了层状黏半空间中一组完备的基本解，也为今后建立以层状黏半空间中球面SH、P和SV波格林函数为基本解的边界元方法求解工程波动问题奠定了基础.

2模型与求解

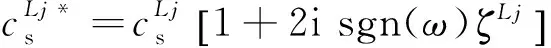
具体求解时，首先通过Hankel积分变换将球面波展开为相应柱面波的叠加，也即将球面波由空间域变换到波数域中；如图2所示，在波数域中将球面波源所在土层上下端面固定，求得固定层内的动力响应，同时计算满足这样条件的相应反力(其中固定层内动力响应以及固定端面反力又分别由相应的特解和齐次解组成)，然后将反力以相反的方向作用到总体系上，采用直接刚度法计算固定端面反力引起的动力响应；叠加固定层内动力响应和固定端面反力产生动力响应，可求得层状黏弹性半空间中任意点波数域中的动力响应；最后采用Hankel积分逆变换，将动力响应由波数域变换到空间域内，求得球面波源空间域内的动力响应，也即层状黏弹性半空间中球面波源自由场.时域自由场则可通过对频域结果的傅里叶逆变换求得.以下将对层状黏弹性半空间的反轴对称(柱面SH波)和轴对称(柱面P-SV波)情况精确动力刚度矩阵的建立和层状半黏弹性空间中球面SH、P和SV的自由场求解进行介绍.

2.1层状黏弹性半空间精确动力刚度矩阵

2.1.1层状黏弹性半空间反轴对称(柱面SH波)精确动力刚度矩阵

假定土层中上行和下行的柱面SH波的势函数为

图1　(a) 层状黏弹性半空间中埋置球面波源； (b) 球面SH、P和SV示意图Fig.1　(a) Buried spherical sources in a layered half-space； (b) Spherical SH-, P- and SV-waves

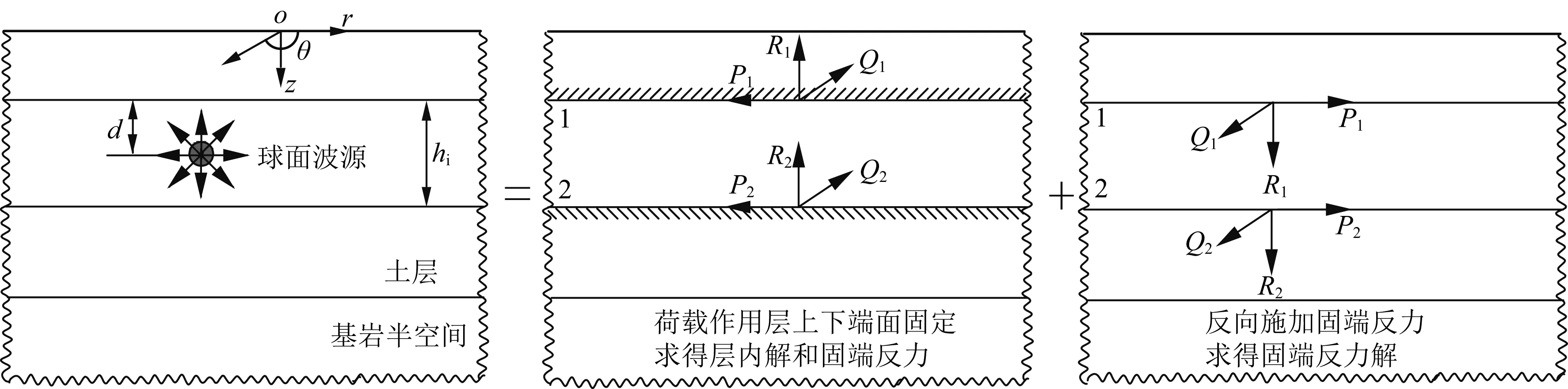
图2　球面波源自由场求解示意图球面波为SH波时，固定层上下端面上仅有剪应力τzθ，固定端面的反力仅有沿环向的力Q1和Q2；球面波为P或SV波时，固定层上下端面上有剪应力τzr和正应力σz，固定端面的反力有沿径向的力P1和P2以及沿竖向的力R1和R2.Fig.2　Diagram for calculation of dynamic responses of buried spherical sourcesFor spherical SH-waves, there is only shear stress τzθ on the top and bottom interfaces of the fixed layer, and there are only the corresponding circumferential reaction forces Q1 and Q2 are exist. For spherical P- and SV-waves, there are shear stress τzr and normal stress σz on the top and bottom interface of the fixed layer, and there are the corresponding radial reaction forces P1 and P2 and vertical reaction forces R1 and R2 exist.

(1)

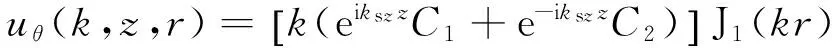
(2)

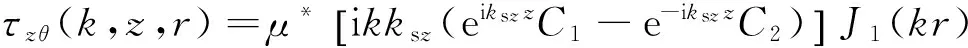
(3)

其中，μ*=μ(1+2isgn(ω)ζ)为复剪切模量.将z=0和z=h(h为土层厚度)分别代入式(2)和(3)，可得土层顶面和底面的位移和应力幅值分别为

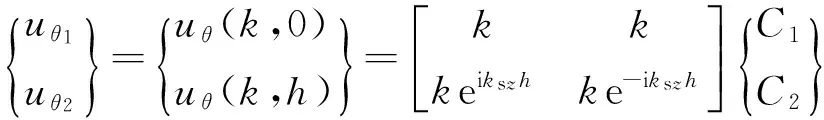
(4)

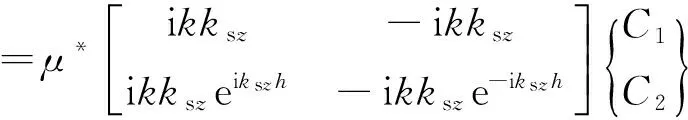
(5)

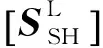
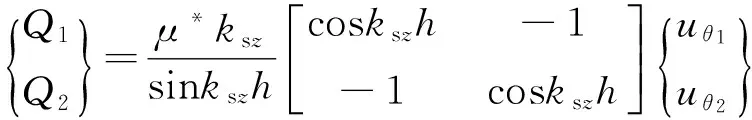
(6)

上标“L”代表土层，在动力刚度矩阵中下标“SH”代表反轴对称运动.

在半空间的表面施加反轴对称荷载，只会产生幅值为C2的去波，以下标“0”表示半空间自由表面，在式(5)和(6)中，令C1=0，Q0=-τz θ0，消去C2得半空间的动力刚度系数SHR为

(7)

由于半空间多用作模拟基岩，故用上标“R”表示.集

(8)

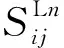
(9)

2.1.2层状黏弹性半空间轴对称(柱面P-SV波)精确动力刚度矩阵

假定土层中上行和下行的柱面P和SV波的势函数为

(10)

(11)

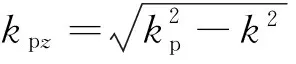
(12)

(13)

将式(10)和(11)代入式(12)和(13)得

(14)

(15)

应力τzr和σz与位移ur和uz之间满足关系式

(16)

(17)

其中，λ*=λ(1+2i sgn(ω)ζ)，将式(14)和(15)代入式(16)和(17)得

(18)

(19)

将z=0和z=h分别代入式(14)、(15)、(18)和(19)，可得土层顶面和底面的位移和应力幅值为

(20)

(21)

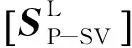
(22)

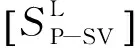
(23)

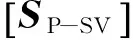
(24)

(25)

2.2层状黏弹性半空间球面波源自由场

2.2.1层状黏弹性半空间中球面SH波自由场

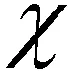
(26)

由式(26)，球面SH波的每个柱面波分量可写为

(27)

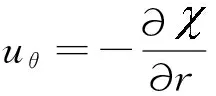
(28)

由τz θ=μ*∂uθ/∂z，可得固定层内的应力特解幅值(以上标“p”表示)为

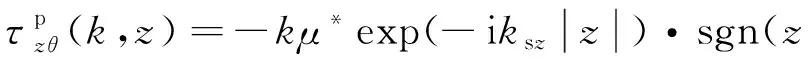
4.遵守党的优良传统。党的优良传统作风是我们党在长期实践中培育起来的体现党的性质、宗旨的做法和习惯，是党保持自身先进性和纯洁性的外在表现。因此，严肃党内政治生活就是要进一步发扬光大党的优良传统作风，形成浩然正气并使之在党内蔚然成风。习近平同志强调：“要坚持和发扬实事求是、理论联系实际、密切联系群众、开展批评和自我批评、坚持民主集中制等优良传统。”[1]

(29)

将z=-d和z=hi-d代入式(28)可求得固定层顶面和底面的位移特解幅值为

(30)

(31)

(32)

(33)

(35)2.2.2层状黏弹性半空间中球面P和SV波自由场

同球面SH情况，空间域内球面P或SV波可通过Hankel变换，展开为波数域内柱面波的叠加：

(36)

(37)

球面P波或SV波的每个柱面波分量在波数域中的势函数可写为

(38)

(39)

将式(38)和(39)代入式(12)和(13)，可得固定层内分别对应球面P和SV波的位移特解幅值为

(40)

(41)

将式(40)和(41)带入式(16)和(17)，可得分别对应球面P和SV波的固定层内应力特解幅值为

(42)

(43)

将z=-d和z=hi-d代入式(40)和(41)可求得分别对应球面P和SV波的固定层顶面和底面的位移特解幅值为

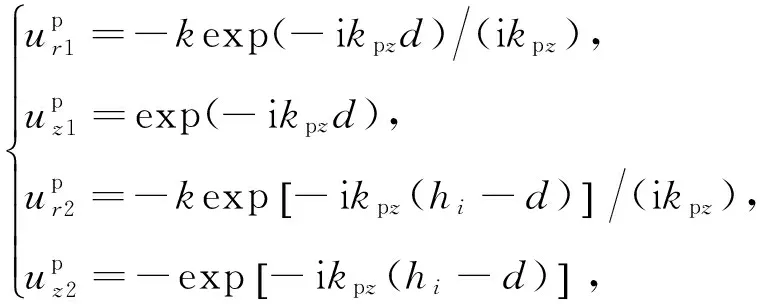
(44)

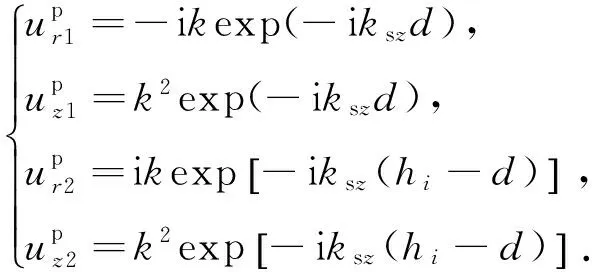
(45)

(46)

(47)

(48)

(49)

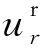
(50)

3方法验证

为验证本文方法的正确性，图3给出本文计算结果与Lamb(1904)给出均匀弹性半空间中埋置球面膨胀P波对应的地表水平和竖向位移幅值的比较，值得注意的是Lamb(1904)中只给出了均匀半空间中埋置膨胀P波自由场的计算公式，并没有给出数值结果，图3中文献结果为按照Lamb(1904)中给出计算公式(142)至(147)求得到的结果.图3中半空间介质泊松比为0.25，取无量纲频率η=ω d/cs=1.0，其中ω为球面膨胀波源振动频率，d为其埋深，cs为剪切波速.图3中连续结果为本文结果，离散结果为按Lamb(1904)计算结果.从图3中可以看出本文结果与Lamb(1904)结果非常吻合，说明了本文方法的正确性.

4数值结果

4.1频域结果分析

4.1.1基岩与土层刚度比对球面波自由场的影响

图3　本文结果与Lamb(1904)结果的比较Fig.3　Comparison with the results given by Lamb (1904)

图4　球面波源为P波时，位移和应力沿深度的变化(基岩与土层刚度比不同)Fig.4　Displacements and stresses along depth for spherical P-waves (different stiffness ratio between the layer and bed rock)

图5　球面波源为SV波时，位移和应力沿深度的变化(基岩与土层刚度比不同)Fig.5　Displacements and stresses along depth for spherical SV-waves (different stiffness ratio between the layer and bed rock)

图6　球面波源为SH波时，位移和应力沿深度的变化(基岩与土层刚度比不同)Fig.6　Displacements and stresses along depth for spherical SH-waves (different stiffness ratio between the layer and bed rock)

图7　球面波源为P波时，地表不同观测点位移幅值频谱(土层厚度不同)Fig.7　Spectrum of surface displacement amplitudes for spherical P-waves (different depth of the layer)

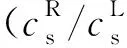
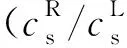
图6给出了球面波源为SH波时，对应不同基岩与土层剪切波速比、位移和应力的实部和虚部沿深度的变化，图6中计算参数仍同图4.与球面P波和SV波不同，球面SH波在半空间中的传播不存在波型转换，也即半空间表面和基岩面产生的反射波仅为球面SH波，因此半空间中仅有环向位移和剪应力，同时图6中的结果也显示在球面SH波作用水平面位置(z/a=1.0)处，环向位移和剪应力均较大.另外，同球面SV结果(图5)相似，基岩上单一土层情况与均匀半空间情况差异要小于球面P波情况，不同基岩与土层刚度比情况的差异也较小.

4.1.2土层厚度对球面波自由场的影响

从图7中可以看出，由于考虑了场地自身的动力特性(具有场地固有频率)，基岩上单一土层情况(h/d=2.0和4.0)对应的地表位移幅值频谱与均匀半空间情况(h/d=∞)有着本质的差异.均匀半空间情况地表位移幅值整体上随频率的增大逐渐减小，而基岩上单一土层情况位移幅值频谱表现为以均匀半空间情况为中心的上下振荡，出现多个峰值频率，且在峰值频率处，基岩上单一土层情况对应地表位移幅值显著大于均匀半空间情况.另外不同土层厚度对应的位移幅值频谱(h/d=2.0和4.0)也有着明显的差异，这是因为土层厚度的改变直接导致了土层自身动力特性的改变，也即改变了球面波在土层中的相干方式.

图8给出了球面波源为SV波时，对应不同土层厚度，地表不同观测点的位移幅值频谱.图8中计算参数同图7.从图8亦可以看出，与球面P波结果(图7)相同，球面波源为SV波时，基岩单一土层情况与均匀半空间情况地表位移幅值有着显著的差别，基岩上单一土层情况存在多个峰值频率，同时随着土层厚度的增大，峰值频率点逐渐向低频迁移.另外，球面SV波情况，土层厚度对位移幅值频谱的影响整体上要低于球面P波情况，尤其在r/d=1.0位置，h/d=4.0与h/d=∞对应的位移幅值频谱非常接近.

图9给出了球面波源为SH波时，对应不同土层厚度，地表不同观测点的位移幅值频谱.图9中计算参数同图7.从图9中可以看出，与球面P波结果(图7)和SV波结果(图8)相同，球面波源为SH时，基岩上单一土层情况与均匀半空间情况地表位移幅值存在较大差异，同时不同的土层厚度也对应不同的位移幅值频谱，但对应于相同的土层厚度，球面SH波对应的峰值频率相对小于球面P和SV波情况.

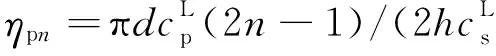
表1　基岩上单一土层固有频率

图8　球面波源为SV波时，地表不同观测点位移幅值频谱(土层厚度不同)Fig.8　Spectrum of surface displacement amplitudes for spherical SV-waves (different depth of the layer)

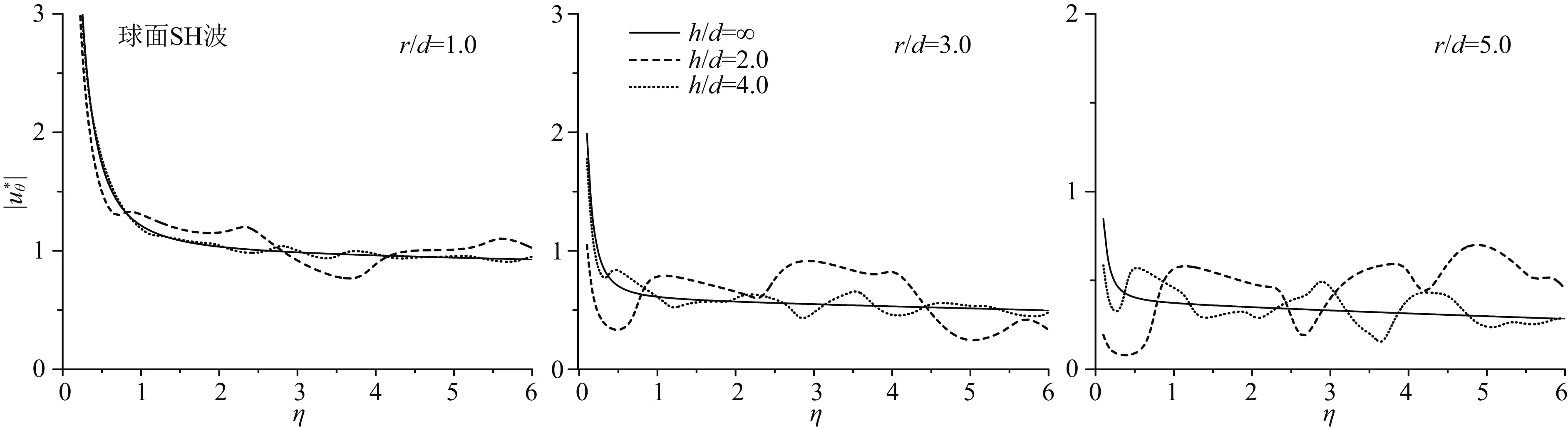
图9　球面波源为SH波时，地表不同观测点位移幅值频谱(土层厚度不同)Fig.9　Spectrum of surface displacement amplitudes for spherical SH-waves (different depth of the layer)

土层厚度观测点峰值频率h/d=2.0h/d=4.0r/d=1.0r/d=3.0r/d=5.0r/d=1.0r/d=3.0r/d=5.0峰值1峰值2峰值1峰值2峰值1峰值2峰值1峰值2峰值1峰值2峰值1峰值2球P|u*r|1.303.651.303.701.303.700.651.850.651.850.651.85|u*z|1.303.651.303.701.353.800.651.800.651.800.651.85球SV|u*r|1.303.651.403.651.403.600.651.850.651.800.651.85|u*z|1.353.651.453.651.453.650.651.850.751.800.751.85球SH|u*|0.852.300.902.901.152.300.451.150.451.150.501.15

4.1.3黏弹性因素对球面波自由场的影响

图10对应不同阻尼比的结果表明，阻尼对位移和应力的实部和虚部均有较为显著的影响.随着阻尼比的增大，位移以及应力的实部和虚部均表现为逐渐变小，尤其在位移和应力的峰值处.另外，比较基岩面以上位置(z/a≤2.0)和基岩面以下位置(z/a>2.0)处的位移和应力发现，阻尼比的变化主要影响基岩面以上位置的动力响应，这是因为基岩面的刚度大于土层的刚度，动力响应主要集中在土层内且阻尼使得位移和应力沿深度衰减所致.

从图11中可以看出，阻尼对基岩上单一土层表面各观测点的位移幅值频谱有着显著影响.随着阻尼比的增大，各观测点位移幅值频谱的峰值显著降低，但阻尼比改变并不改变位移幅值频谱的峰值频率.阻尼对位移幅值的影响，随着频率的增大逐渐增大，尤其在峰值频率处.对比不同阻尼比径向和竖向位移幅值频谱发现，阻尼对径向位移幅值频谱的影响更为明显.对比不同观测点位移幅值频谱发现，阻尼对距离波源更远观测点(r/d逐渐增大)的影响更为明显，尤其在较高频率处(η>4.0).

4.2时域结果分析

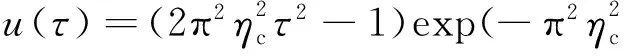
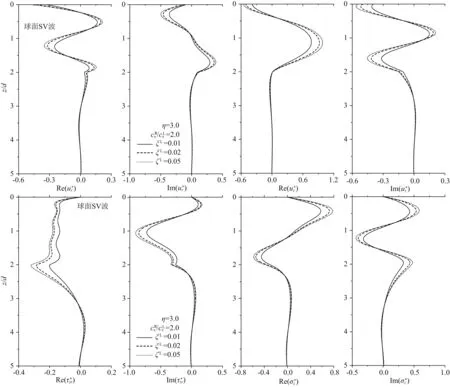
图10　球面波源为SV波时，位移和应力沿深度的变化(阻尼比不同)

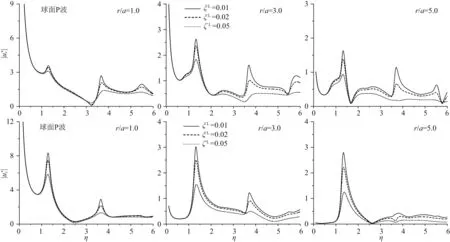
图11　球面波源为P波时，地表不同观测点位移幅值频谱(阻尼比不同)Fig.11　Spectrum of surface displacement amplitudes for spherical P-waves (different damping ratio)

图12　(a) 球面波为SH波时，地表位移时程(均匀半空间)；(b)球面波为P波时，地表位移时程(均匀半空间)； (c) 球面SV波时，地表位移时程(均匀半空间)Fig.12　(a) Time histories of displacement amplitudes for spherical SH-waves (uniform half-space)；(b) Time histories of displacement amplitudes for spherical P-waves (uniform half-space); (c) Time histories of displacement amplitudes for spherical SV-waves (uniform half-space)

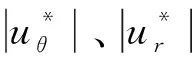
从图12中可以清晰看出球面波的传播过程.对于图12a所示的球面SH波，由于其不存在波型转换现象，直达SH波传播到地表后，反射波也仅为SH波，所以在地表仅存在传播的SH波迹线.同球面SH波不同，对于图12b所示球面P波，存在波型转换现象，直达P波到达地表后，会同时产生反射的P波和SV波，因此在地表可观测到以较快速度传播的P波迹线和以较慢速度传播的SV波迹线，同时球面P波情况，主要能量由P波携带，因此对于任一观测点，先发生以较快速度较强能量传播来的P波振动，再发生以较慢速度较弱能量传播来的SV波振动，且地表观测点越远，P波和SV波到达的时间差越大.同球面P波情况相同，图12c所示的球面SV波亦存在波型转换问题，因此地表也出现P波和SV波两条迹线，但球面SV波情况，主要能量由SV波携带，因此对于任一观测点，先发生以较快速度较弱能量传播来的P波振动，再发生以较慢速度较强能量传播来的SV波振动.

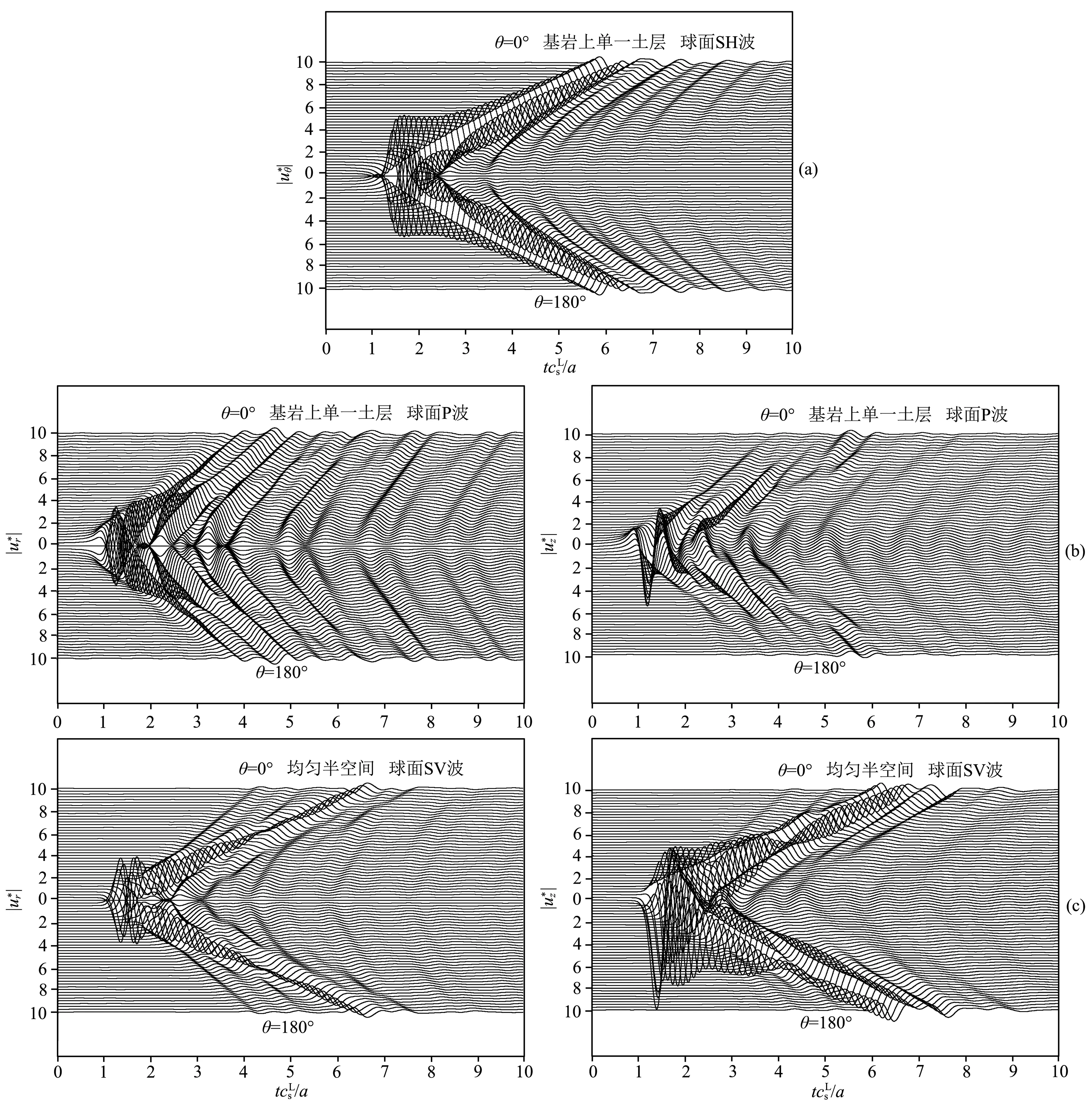
图13　(a) 球面SH波时，地表位移时程(基岩上单一土层)；(b) 球面P波时，地表位移时程(基岩上单一土层)；(c) 球面SV波时，地表位移时程(基岩上单一土层)Fig.13　(a) Time histories of displacement amplitudes for spherical SH-waves (single layered half-space)； (b) Time histories of displacement amplitudes for spherical P-waves (single layered half-space)； (c) Time histories of displacement amplitudes for spherical SV-waves (single layered half-space)

图14　球面SH波时，地表位移时程(不同阻尼比)

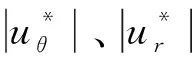
比较图12中均匀半空间结果与图13中基岩上单一土层结果发现，对于球面SH、P和SV波均表现出基岩上单一土层情况对应的地表位移幅值时程较均匀半空间情况要复杂的多，同时地表位移的振动时间也有明显的延长，这是由于波在土层中来回反射形成的(对于均匀半空间情况，反射波传向无穷远处，不会再返回).球面P波和SV波情况，土层中同时存在来回反射的P和SV波，而球面SH波情况，土层中仅存在来回反射的SH波，因此图13b和图13c对应的球面P和SV波位移时程较图13a对应的SH波位移时程更为复杂.

5结论

基于柱面SH、P和SV波的势函数，在柱坐标系下分别建立了黏弹性土层和半空间的反轴对称(柱面SH波)和轴对称(柱面P-SV)波的精确动力刚度矩阵，进而采用刚度矩阵方法结合Hankel积分变换给出了层状黏弹性半空间中球面SH、P和SV波自由波场的计算公式.文中以均匀半空间和基岩上单一土层中球面SH、P和SV波的自由波场为例，分别在频域和时域内进行了数值计算分析，得到了以下主要结论.

(1) 基岩面的存在使得球面波在土层中多次反射，进而使得基岩上单一土层中球面波自由波场与均匀半空间情况有着本质的差异.通过对不同基岩与土层剪切波速比的结果分析发现，基岩与土层剪切波速比的变化对球面P波自由场的影响大于球面SV和SH波自由场的影响.

(2) 基岩上单一土层对应的球面波自由场位移幅值频谱存在多个峰值频率，球面P和SV波对应的第1和第2峰值频率与按P波波速计算求得场地第1和第2阶固有频率非常接近，而球面SH波对应的第1和第2峰值频率则与按S波波速计算求得场地第1和第2阶固有频率非常接近.

(3) 球面波源为球面P或SV波时，均匀半空间地表可观测到以较快P波波速和以较慢S波波速传播的两条迹线，而球面SH波仅存在以S波传播的一条迹线.基岩上单一土层中情况的地表点的位移时程较均匀半空间情况要复杂的多，同时振动时间也有明显延长.

(4) 阻尼的增大会显著降低位移幅值频谱的峰值，但不改变峰值频率，且随着频率的增大，阻尼的影响更加明显.随着阻尼比的增大，地表位移幅值逐渐减小的同时振动持续时间明显缩短.

附录

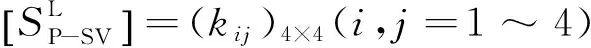
k14=(coskpzh-coskszh)/D,

k23=(-coskpzh+coskszh)/D,

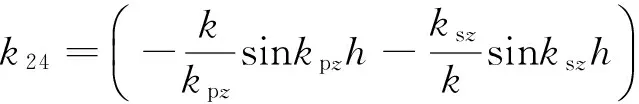
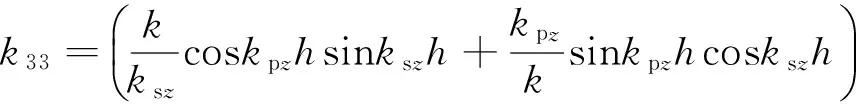
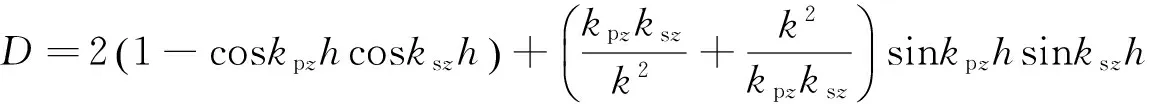
k21=k12； k31=k13； k32=k23； k41=k14； k42=k24； k43=k34.

References

Gao Y F, Jin J X, Xie K H, et al. 1999. General solution to the soil seismic response on stratified foundations.ChineseJournalofGeotechnicalEngineering(in Chinese), 21(4): 498-500.

Haskell N A. 1953. The dispersion of surface waves on multilayered media.Bull.Seismol.Soc.Am., 43(1): 17-34.

Idriss I M, Seed H B. 1968. Seismic response of horizontal soil layers.JournaloftheSoilMechanicsandFoundationsDivision, 94(4): 1003-1031.Jin X, Kong G, Ding H P. 2004. Nonlinear seismic response analysis of horizontal layered site.EarthquakeEngineeringandEngineeringVibration(in Chinese), 24(3): 38-43.

Kausel E, Roёsset J M. 1981. Stiffness matrices for layered soils.Bull.Seismol.Soc.Am., 71(6): 1743-1761.

Lamb H. 1904. On the propagation of tremors over the surface of an elastic solid.Phil.Trans.Roy.Soc.London,Ser.A, 203(359-371): 1-42.Li S Y, Wang X L, Zhou Z H. 2003. The time-step numerical simulation of free field motion of layered half-space for inclined seismic waves.JournalofJilinUniversity(EarthScienceEdition) (in Chinese), 33(3): 372-376.

Li X J. 1987. Seismic response analysis of soil layer and visco-elastoplastic model [Ph.D.] (in Chinese). Harbin: Institute of Engineering Mechanics, China Seismological Bureau, 34-51.

Liang J W, You H B. 2004. Dynamic stiffness matrix of a poroelastic multi-layered site and its green′s functions.Earthq.Eng.Eng.Vib., 3(2): 273-282.

Liang J W, Zhang A J, He Y. 2014. 2-D inversion of obliquely incident earthquake ground motion in layered elastic half-space.JournalofVibrationEngineering(in Chinese), 27(3): 441-450.

Lin C H, Lee V W, Trifunac M D. 2005. The reflection of plane waves in a poroelastic half-space saturated with inviscid fluid.SoilDyn.Earthq.Eng., 25(3): 205-223.

Liu J B, Wang Y. 2006. A 1-D time-domain method for 2-D wave motion in elastic layered half-space by antiplane wave oblique incidence.ChineseJournalofTheoreticalandAppliedMechanics(in Chinese), 38(2): 219-225.Luan M T, Lin G. 1992. Computational model for nonlinear analysis of soil site seimic response.EngineeringMechanics(in Chinese), 9(1): 94-103.

Thomson W T. 1950. Transmission of elastic waves through a stratified solid medium.J.Appl.Phys., 21(2): 89-93.

Wolf J P, Obernhuber P. 1982a. Free-field response from inclined SV- and P-waves and Rayleigh-waves.Earthq.Eng.Struct.Dyn., 10(6): 847-869.

Wolf J P, Obernhuber P. 1982b. Free-field response from inclined SH-waves and Love-waves.Earthq.Eng.Struct.Dyn., 10(6): 823-845.Xue S T, Chen J, Chen R, et al. 2000. The response analysis of damped TI layered soil for incident SH-waves.JournalofVibrationandShock(in Chinese), 19(4): 54-56.

Xue S T, Xie L Y, Chen R, et al. 2004. Dynamic analysis of response of transversely isotropic stratified media to incident P-SV waves.ChineseJournalofRockMechanicsandEngineering(in Chinese), 23(7): 1163-1168.

附中文参考文献

高玉峰, 金建新, 谢康和等. 1999. 成层地基一维土层地震反应解析解. 岩土工程学报, 21(4): 498-500.

金星, 孔戈, 丁海平. 2004. 水平成层场地地震反应非线性分析. 地震工程与工程振动, 24(3): 38-43.

李山有, 王学良, 周正华. 2003. 地震波斜入射情形下水平成层半空间自由场的时域计算. 吉林大学学报(地球科学版), 33(3): 372-376.

李小军. 1987. 粘弹塑性模型及土层地震反应分析[博士论文]. 哈尔滨: 国家地震局工程力学研究所, 34-51.

梁建文, 张爱娟, 何颖. 2014. 层状弹性场地基岩斜入射地震动二维反演. 振动工程学报, 27(3): 441-450.

刘晶波, 王艳. 2006. 成层半空间出平面自由波场的一维化时域算法. 力学学报, 38(2): 219-225.

栾茂田, 林皋. 1992. 场地地震反应一维非线性计算模型. 工程力学, 9(1): 94-103.

薛松涛, 陈军, 陈镕等. 2000. 有限尼TI层状场地对平面入射SH波的响应分析. 振动与冲击, 19(4): 54-56.

薛松涛, 谢丽宇, 陈镕等. 2004. 平面P-SV波入射时TI层状自由场地的响应. 岩石力学与工程学报, 23(7): 1163-1168.

(本文编辑胡素芳)

基金项目国家自然科学基金(51578373，51578372),天津市应用基础及前沿技术研究计划(12JCQNJC04700)资助.

作者简介巴振宁，男，1980年生，博士，副教授，主要从事地震工程研究.E-mail:bazhenning_001@163.com

doi:10.6038/cjg20160218 中图分类号P315

收稿日期2015-01-24，2015-08-17收修定稿

Free-field responses of spherical SH-, P- and SV-wave sources in a layered visco-elastic half space

BA Zhen-Ning1,2, LIANG Jian-Wen1,2, ZHANG Yan-Ju1

1DepartmentofCivilEngineering,TianjinUniversity,Tianjin300072,China2KeyLaboratoryofCoastalStructuresinCivilEngineeringandSafetyofMinistryofEducation,Tianjin300072,China

AbstractFree-field responses of spherical sources embedded in a half-space, especially in a layered half-space is of fundamental importance in studying various wave scattering problem and soil-structures interaction problem. However, few studies have been reported to investigate the free-field responses of spherical sources. In this paper, dynamic responses of spherical SH-, P- and SV-wave sources embedded in a layered visco-elastic half-space are studied.

KeywordsSpherical sources; Free-field response; Direct stiffness method; Layered visco-elastic half-space; Hankel transformation

巴振宁，梁建文，张艳菊. 2016. 三维层状黏弹性半空间中球面SH、P和SV波源自由场.地球物理学报，59(2):606-623,doi:10.6038/cjg20160218.

Ba Z N, Liang J W, Zhang Y J. 2016. Free-field responses of spherical SH-, P- and SV-wave sources in a layered visco-elastic half space.ChineseJ.Geophys. (in Chinese),59(2):606-623,doi:10.6038/cjg20160218.