复合地层土压平衡盾构斜穿地下连续墙推进力计算研究
——以南宁市轨道交通5号线新广区间盾构隧道工程为例
2021-10-18肖昌军陆云贤付循伟王树英
肖昌军, 陆云贤, 周 志, 付循伟, 王树英
(1. 中铁广州工程局集团城轨工程有限公司, 广东 广州 511459; 2. 中南大学土木工程学院, 湖南 长沙 410075)
0 引言
近年来我国盾构隧道建设得到了快速发展,地铁运营里程逐年增加,在开通的地铁线路中,盾构隧道占据了较大的比重。为满足功能需求和交通规划,施工面临的周边环境日益复杂,经常需要穿越桩基、地下连续墙(简称地连墙)、既有地下建筑物等[1-3]。因此,盾构隧道开挖面破岩对象动态变化,刀盘受力不均。若推进力得不到很好的调控,盾构姿态控制难度加大,则不能保证盾构的掘进轴线与设计轴线一致[4-6]。
盾构隧道施工中盾构推进的方向主要是通过改变推进千斤顶的推进力值来操控的,目前主要依靠盾构操作司机的经验来确定。因此,分析盾构在掘进施工中的整体受力,尤其是姿态偏转及掘削不同破岩对象的情况下,给出推进千斤顶推进力的表达式是很有必要的。由于对盾构周围所受的力无法准确地考虑及计算表达,使得盾构整体力学模型难以精确建立。因此,许多学者在建立盾构掘进力学模型以及姿态控制等方面进行了一系列研究。Komiya等[7]运用鲁棒理论进行盾构姿态的控制研究。Sugimoto等[8]研究了盾构推进力与地层土压力的关系,基于盾构的整体受力平衡,同时考虑土压力与姿态控制的关系,建立了盾构推进力的理论模型。管会生[9]通过研究盾构与土的相互作用关系,研究盾构设备力学参数与力学行为的模型解析,为铰接式盾构的受力分析研究提供了新的理论思路。沈翔等[10]研究了盾构中俯仰角这一关键的姿态控制参数对盾构-土相互作用的影响,提出了盾构俯仰角的计算方法,并与实际工程进行了对比分析。综上,目前对于盾构姿态控制的研究更多的是一些控制理论的应用,虽有一定的理论计算模型,但考虑因素欠缺,并未系统地考虑盾构-土相互作用、盾构姿态参数以及刀具破岩荷载的影响。
本文依托南宁市轨道交通5号线新秀公园站—广西大学站区间盾构斜向穿越1号线广西大学站既有地连墙工程,为了使盾构斜向磨墙后短距离内安全抵达洞门完成接收,对姿态参数、掘进参数影响下斜向穿越地连墙的盾构推进荷载理论模型展开研究。通过考虑刀具破岩的影响,根据不同刀具破岩荷载计算公式,求解开挖面中多种破岩对象对应的刀盘阻力,进而得到不同破岩工况下的推进力值,并与实测值进行对比,总体误差满足工程需求,以期研究结果为类似工程提供参考。
1 工程概况
南宁市轨道交通5号线新广区间,南起新秀公园站,沿明秀西路向北抵达广西大学站,包括1站1区间,标段总长1 682.3 m,其中,车站长359.2 m。新广区间在明秀路口下穿既有1号线广西大学站,下穿范围地连墙均为玻璃纤维筋混凝土结构,斜穿地连墙后距离接入5号线广西大学站最短仅有8 m,盾构推进力与姿态控制难度较大。双线盾构隧道斜向穿越既有车站地连墙模型见图1。
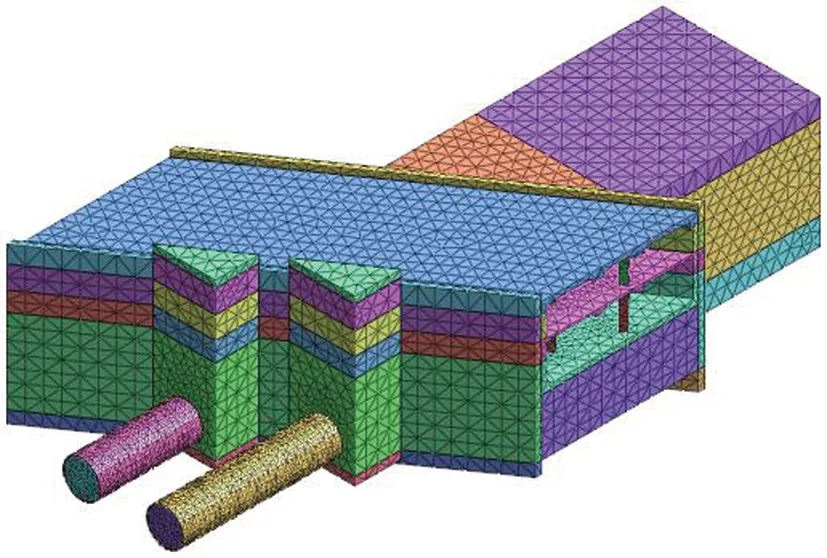
图1 双线盾构隧道斜向穿越既有车站地连墙模型图
2 刀具破岩荷载计算方法
2.1 盘形滚刀法向破岩力计算
一般来说,盾构刀盘上的盘形滚刀在破岩过程中与岩石之间的相互作用力有: 法向推压力FV,指向开挖面;切向滚动力FR,指向滚刀切向;侧向力FS,指向刀盘中心,如图2所示。
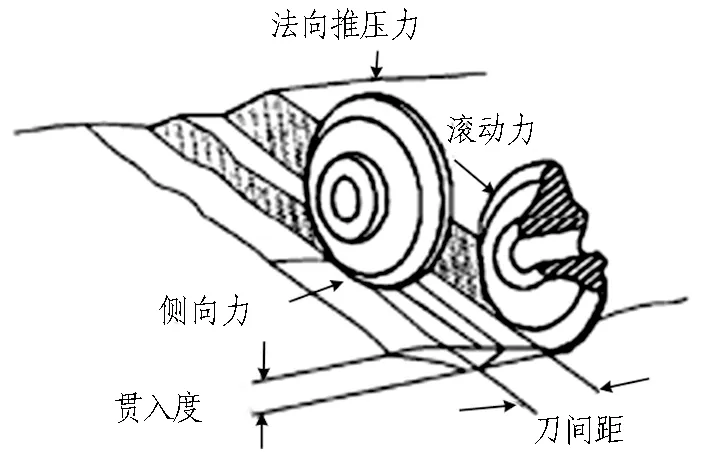
图2 盘形滚刀三维受力简图[11]
针对盘形滚刀作用在隧道开挖面上的法向推压力FV,即法向破岩力,参考吴起星[12]对盘形滚刀破岩机制的分析,选用式(1)进行计算。该公式由4个参数表述,可通过简单的基本岩石试验测得,因此应用较为广泛。
(1)
式中:FV为盘形滚刀法向破岩力;E为岩石弹性模量;h为盘形滚刀贯入度;σc为岩石单轴抗压强度;s为相邻盘形滚刀刀刃间距。
2.2 刮刀法向破岩力计算
对于刮刀切削软土的受力模型,以刮刀的平面受力为基础,然后拓展到三维。刮刀的工作参数及整体受力示意如图3所示。
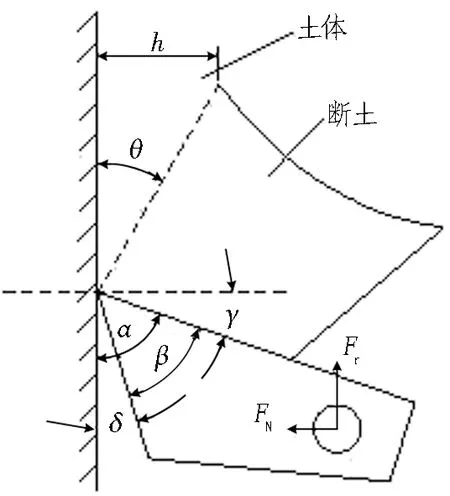
图3 刮刀的工作参数及整体受力示意图[13]
图3中刮刀的工作参数有: 前角γ,后角δ,刃角β,切削角α。各个角度之间满足如下关系:α=β+δ,α+γ=90°。土体在刀具剪切力的作用下断裂,断土沿着刀具前刀面流出,土体剪切破裂面与切削平面之间的夹角为θ。由土力学原理可知,θ=0.5×(90°-φ),其中,φ为土体的内摩擦角。
杜志国[13]对刮刀切削土体进行受力分析,并进一步推导得到刮刀垂直开挖面方向的分力FN,即法向破岩力,如式(2)所示。
FN=μ0N0sinα-N0cosα。
(2)
式中:μ0为刀刃与土体接触面的摩擦因数;N0为刀刃与土体接触面的法向力,可由断土的受力平衡求得,具体推导过程参见文献[13];α为刮刀切削角。
3 盾构推进力理论计算方法
3.1 盾构推进荷载理论模型
沈翔等[10]在Sramoon等[14]、Sugimoto等[15]对盾构推进荷载计算研究的基础上,将盾构的盾壳与围岩的接触关系矢量化,将围岩对盾构每个单元的作用力分别沿盾构的法线、切线和轴线进行分解,得到的荷载模型如图4所示。图4中盾构受到的荷载有: 盾构设备自重荷载f1,盾尾与管片之间的油脂压力荷载f2,盾构设备推进油缸提供的推进荷载f3,盾构刀盘在开挖面所受的荷载f4,盾壳外围的围岩荷载f5。
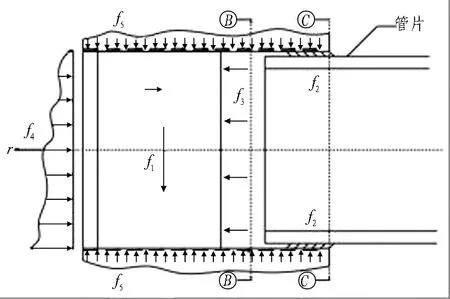
图4 盾构荷载模型[10]
3.2 作用荷载计算方法
参考Sugimoto等[8]对作用荷载f1、f2、f5的定义求解,即可得到相应的作用荷载矢量值。对于作用于刀盘的掘进界面荷载f4,是本文研究的重点,将在4.2节结合实例进行详述。
对于千斤顶提供的推进荷载f3,将推进油缸千斤顶的推进力分为上、下、左、右4个部分,即有4个未知量。通过MATLAB软件将所有盾构作用荷载进行矢量化编程,即通过各作用荷载的定义方法在程序中计算出矢量力后使用列向量表示,通过简单的坐标变换将所有荷载转化到统一的盾构坐标系(见图5)中,输入初始计算参数后可分别求解得到除f3外的其余作用荷载。在盾构荷载模型中,通过静力平衡方程(式(3)),运用6个方程求解4个未知量,属于超定方程组求解,难以求得解析解。因此,在MATLAB计算程序中通过最小二乘法求解6个函数方程,可解得近似的数值解,即为分区推进力。
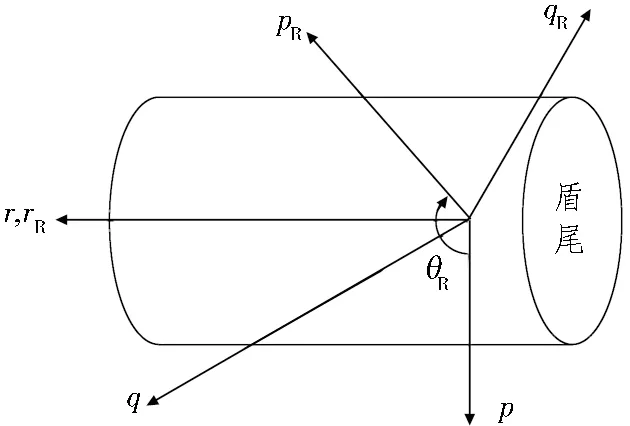
图5 盾构坐标系示意图
(3)
式中:Fi为盾构某一作用荷载的矢量力;Mi为盾构某一作用荷载的矢量力矩;i为盾构各作用荷载代号,i=1,2,3,4,5;M为盾构整体坐标系。
图5中,盾构整体坐标系为(p,q,r),将盾构整体坐标系绕r轴转动θR,即为离散化单元坐标系(pR,qR,rR)。因此,对于盾构每一个单元的矢量力可以通过坐标变换到整体坐标系中表示[9]。
4 斜穿地连墙盾构推进力计算实例分析
4.1 确定开挖面掘进破岩工况
南宁市地铁5号线新广区间下穿1号线广西大学站地连墙,其俯视图如图6所示。该盾构隧道左右线均呈55°角斜向穿越素桩加固区和玻璃纤维筋地连墙,盾构开挖面范围内土层分布是上圆砾下泥岩,圆砾、泥岩体积比为4∶2~5∶1。
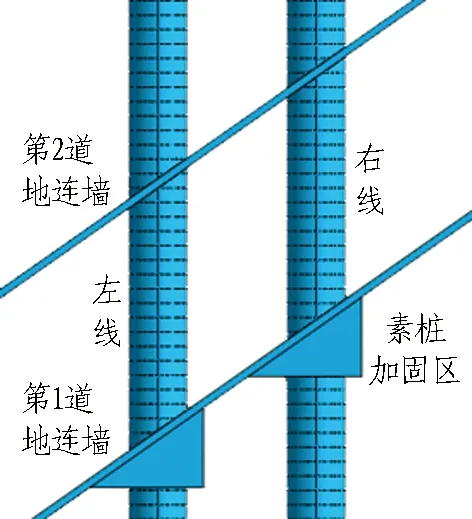
图6 隧道斜穿地连墙俯视图
盾构下穿广西大学站的过程中,开挖面掘进破岩对象动态变化,总共有4种破岩对象,分别为素桩、地连墙、圆砾层和泥岩层。盾构斜向穿越地连墙的过程中,破除地连墙的刀盘作用区域随着盾构的推进是不断变化的,总体呈现从左向右移动的趋势。因此,综合考虑破岩对象的类型和刀盘作用区域的变化,将整个盾构隧道斜穿地连墙的过程分为7种工况,如图7所示。其中,工况1—4为盾构斜穿第1道地连墙;工况5—7为盾构斜穿第2道地连墙。

(a) 工况1: 素桩 (b) 工况2: 地连墙+素桩 (c) 工况3: 圆砾、泥岩层+地连墙+素桩 (d) 工况4: 圆砾、泥岩+地连墙
4.2 作用于刀盘的掘进界面荷载计算
4.2.1 掘进界面荷载组成
盾构推进时作用于刀盘的掘进界面荷载由掘削岩土的阻力f41和舱压阻力f422个部分组成[16]。其中,掘削岩土的阻力f41可由第2节的刀具破岩荷载计算确定,舱压阻力f42可根据水土压力确定。
4.2.2 既定刀盘布置下刀具推进力静态分析
为了适应圆砾土、粉砂质泥岩层以及需切削2道地连墙的工程情况,盾构刀盘主要配有滚刀和刮刀2种刀具,如图8所示。
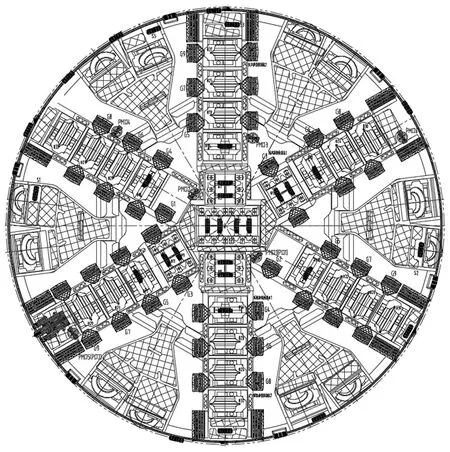
图8 刀盘刀具配置
将原有刀盘刀具配置进行适当简化,得到可用于推进力计算的刀盘刀具配置简图,如图9所示。其中,刀盘有效计算开口率为34%。运用第2节的刀具破岩荷载计算方法,求解得到单把滚刀的法向破岩力FV和单把刮刀的法向破岩力FN。
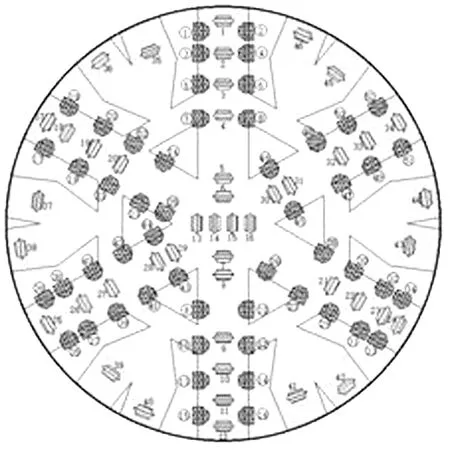
图9 刀盘刀具配置简图
4.2.3 刀盘刀具推进力分配
本工程所用盾构的推进系统共30根油缸,分成4组布置,如图10所示。
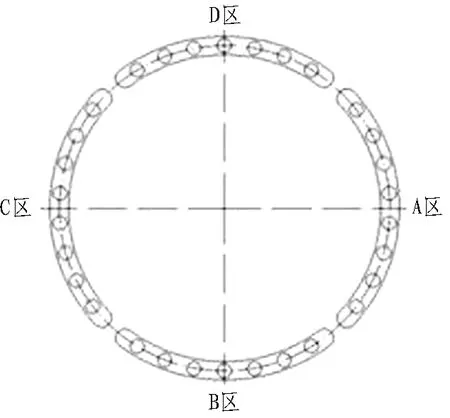
图10 盾构推进液压油缸分区
通过理论计算,得到各掘进破岩工况下的刀具掘削岩土阻力f41和舱压阻力f42。根据盾构推进系统的构造,将刀盘各区域推进力有效分配至推进系统的4组油缸上。
4.3 盾构作用荷载计算参数
土压平衡盾构斜向穿越既有车站地连墙的有关计算参数如表1所示。
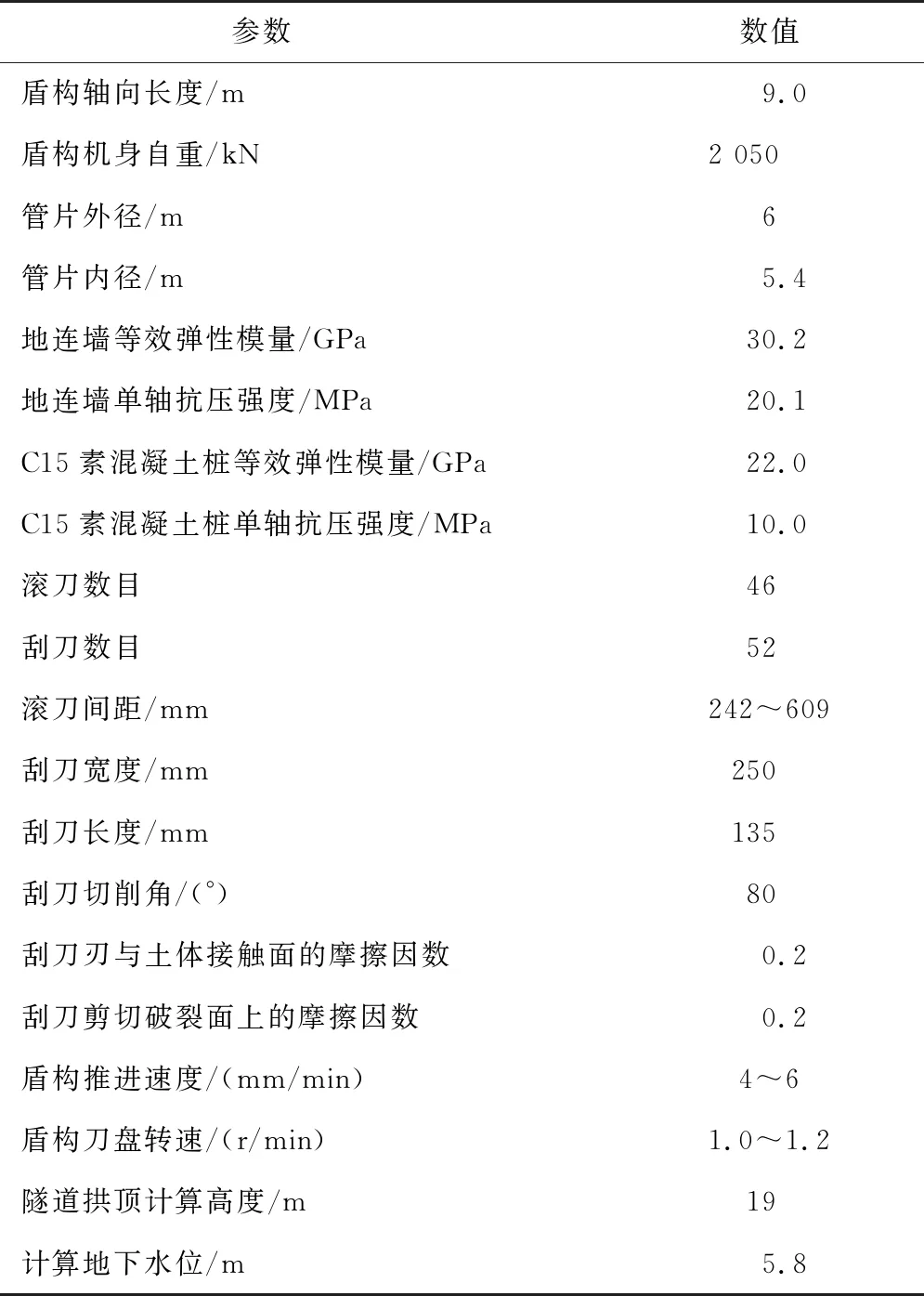
表1 土压平衡盾构作用荷载计算参数
新广区间下穿广西大学站工程范围内自上而下分布有素填土、粉质黏土、粉土、砾砂、圆砾及粉砂质泥岩。各土层参数如表2所示。
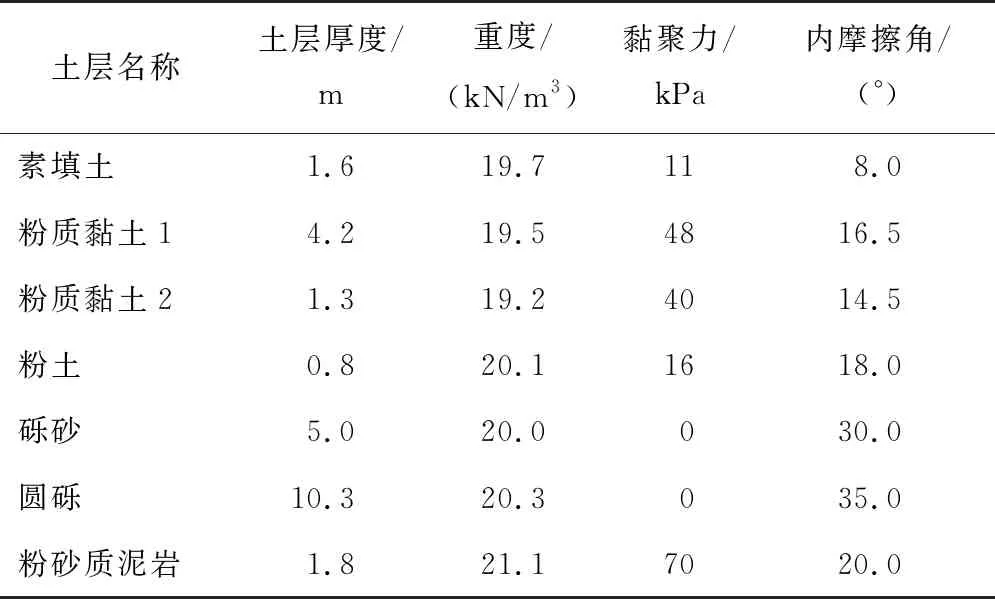
表2 土层参数
4.4 盾构荷载模型计算离散化
为方便MATLAB编程计算荷载模型,将盾壳曲面及刀盘平面均匀地划分为有限个单元,即盾构离散化,沿着径向分成l份,沿着环向分成m份,沿着轴向分成n份,如图11所示。划分单元的数目越多,离散化程度越高,计算越精细,但会增加大量的计算时步。为提高求解效率,在保证最终解较大精度的前提下,降低模型时间复杂度,选用较小的离散程度,此处取l=4,m=40,n=30。
4.5 推进力计算结果及对比
基于3.1节盾构推进荷载理论模型,通过MATLAB编写推进力计算程序,输入盾构作用荷载计算参数,运行得到南宁市轨道交通5号线新广区间斜穿既有广西大学站地连墙的盾构各分区推进力及总推进力值,并与导出的推进力实测值(每环有效推进力的平均值)进行对比。此处以右线下穿段为例进行分析,结果如图12所示。
由图12可以发现,右线下穿段盾构推进力计算总体误差在20%左右,整体满足工程要求,尤其对穿越第2道地连墙的计算效果更好。究其原因,盾构斜向穿越地连墙属于动态破岩过程,盾构下穿素桩与第1道地连墙时,开挖面处的破岩对象最为复杂,盾构周围荷载计算难度大;盾构下穿第2道地连墙时,开挖面处的破岩对象相对简单,理论计算更加准确。
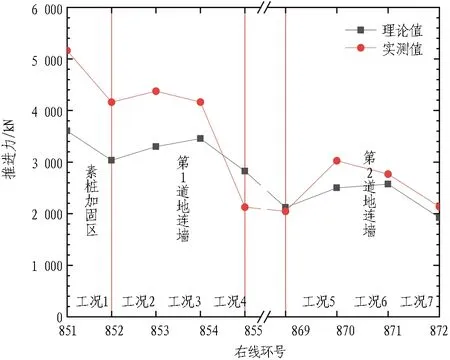
(a) A区推进力
左右线下穿范围的线路均位于R=400 m的缓和曲线上,均以2‰的上坡坡度下穿1号线广西大学站。本文采用的盾构推进荷载计算模型中,虽然已考虑坡角及盾构偏转的影响,但由于实际施工中盾构动态纠偏,盾构铰接角和偏转值实时变化,与静态时的推进力计算存有一定的误差。
5 结论与建议
南宁市地铁5号线新广区间下穿1号线广西大学站,为保证下穿段斜向穿越2道地连墙的安全性,结合盾构推进荷载理论计算和现场实测数据,进行盾构下穿段的推进力分析,并对类似工程盾构掘进参数提出建议。
1)通过盾构推进荷载理论模型,考虑刀盘刀具破岩荷载以及盾构-土相互作用的影响,进行盾构推进荷载的推导计算。
2)结合复合地层下盾构斜穿地连墙的实例计算,验证了盾构推进荷载理论模型的合理性,计算误差总体满足工程要求,下穿段总推进力宜控制在15 000~20 000 kN。
3)盾构在穿越地连墙时需要“低速慢磨”,推进速度宜控制在4~6 mm/min,刀盘转速宜控制在1.0~1.2 r/min,必须降低磨削地连墙对车站整体结构的影响。
4)盾构推进油缸的分区推进力需根据设计轴线、盾构姿态、开挖面硬岩分布情况等综合考虑。若姿态调整较小,可参考本文的理论计算,给出分区推进力的建议参考值,以更好地进行盾构斜穿地连墙的姿态调控。
5)针对实际施工中的盾构动态纠偏问题,后续研究中还需对盾构铰接角和偏转值的动态变化进行相应的算法优化。
