基于分层布局思想的配电网拓扑图自动生成算法

杨贵云，吴倩，曹彦昆，侯晓宇，孙华，王践

（天地电研(北京)科技有限公司，北京市 昌平区 102206）

0 引言

面对电网的“差异化”用电、可靠性要求，以及国家电网公司日益强化的“精益化管理”的要求，亟待对配电网实施以问题诊断为基础、以远景目标网架为导向、以项目落地为目标的规划工作。

配电网规划工作注重宏观网架结构[1-6]，直接在地理信息系统(geographic information system，GIS)接线图上做规划非常不方便，原因如下：GIS图中主干接线不清晰，且图中涉及的细节太多；在杂乱无章的接线图上无法辨识电网问题，进而无法制定方案及贯彻以问题导向、以目标引领的规划思路，规划结果在GIS图上也无法很好地得到展现和解释。

为了便于审查规划项目，需要从多个维度分时间、分空间、依指标、按地理接线、按拓扑接线等方式出图出表，使之化繁为简、分而审之。网格化规划图表多，任务重，遇到上级电源、市政规划、导向目标、政策环境发生变化时，所有年份图纸都要修改，所有相关表格都要重做，工作量极大。如果开发出能够自动成图的规划工具，将大大节省人力[7]。

综上，开发出自动生成拓扑接线图的网格化规划软件是十分必要的。而拓扑生成算法正是自动生成配电网拓扑接线图的核心[8]。

拓扑图的生成涉及图形的自动布局问题[9]，至今都没有很好的算法，拓扑图自动生成算法的实现难度包括以下方面[10]：

1）对象的摆放。对象包括变电站、开关站(开闭所)、变压器等，这些对象对整个图形的布局起到了决定性的作用，其位置将会影响拓扑图的可读性。

2）线路的自动正交化。在拓扑图上，所有的线路都是横平竖直排列，平行线路之间的距离要相等。

3）线路的交叉最小化。在拓扑图上必须尽量保证尽可能减少正交跨越。

已有的拓扑算法大多是基于优化函数的，目标是使图中的交叉最小化[11]。其中：有些算法需要经过很多次迭代(耗时很长)才能获得最优或次优解，如改进遗传算法[12]；有些算法虽然对于少量馈线的布局具有良好的效果，但随着馈线和变电站数量的增加，算法很难收敛，如模拟退火算法[13]。因此，目前对于网格化规划仍没有成熟和适用的算法。

本文通过横向对比各大主流拓扑生成算法、深度挖掘现状拓扑图生成的痛点问题，基于分层求解的思想，借鉴图论的知识，利用深度优先遍历(depth first search，DFS)算法，提出拓扑图自动生成算法。该算法避免了因直接一次性求取所有设备在接线图中合理坐标而可能导致的求解过程高度复杂甚至无解的问题，降低了空间复杂度。另外，每层布局都使用深度优先遍历算法，降低了软件开发的难度。最后，通过工程实际应用，验证了该算法的有效性和适用性。

1 配电网拓扑图自动生成算法的基本思路

拓扑图自动生成算法的目的是求出配电网中每个设备在图纸中的具体位置，即X轴和Y轴坐标。为了实现横平竖直排布设备的要求，本文借助二维数组找出每个设备在图纸中的行、列序号，实现等间距布置。

1.1 分层布局的思想

拓扑图自动生成的实现分为3层：第1层是确定单条馈线的拓扑布局；第2层是确定两两变电站之间所有馈线的拓扑布局；第3层是确定所有变电站之间的拓扑布局。其中，第1层是基础，目的是确定某一条馈线的拓扑接线，包括主干线和分支线。第2层是将每2个互有联络的变电站之间所有馈线的连接关系确定下来。第3层是确定各变电站在图纸上的坐标位置及连接情况，即在所有变电站之间的布局数组中插入两两变电站之间的布局数组，就得到了整个配电网的拓扑布局数组。

实现这种拓扑图自动生成算法，需要分以下5个步骤：

1）生成单条馈线的布局数组。通过DFS算法，将单条馈线上主干线和各分支线上的各设备及其相互之间的连接关系用二维数组的形式保存起来，生成单条馈线的布局数组。

2）生成两两变电站之间所有馈线的布局数组。在单条馈线拓扑图的基础上，将两两变电站之间所有馈线的连接关系用二维数组的形式保存起来，生成两两变电站间的布局数组。

3）生成所有变电站之间的布局数组。所有变电站之间的布局数组用于确定变电站间的布局。将所有电源和变电站抽象为图的顶点，将两两变电站之间的连线抽象为边。将所有变电站之间的连接关系用二维数组的形式保存起来，生成所有变电站间的布局数组。

4）生成配电网全网的布局数组。将两两变电站之间所有馈线的布局数组插入所有变电站之间的布局数组中，便可生成配电网全网的布局数组。

5）生成配电网全网的拓扑接线图。根据配电网全网的布局数组，计算出各节点的行、列序号，即可生成配电网全网的拓扑接线图。

1.2 有向图中两点间最大距离的求解算法

有向图中两点间最大距离的求解算法用于确定各设备在拓扑图中的X轴坐标。配电网中单条馈线的布局数组、两两变电站间布局数组、所有变电站间布局数组的确定都是基于求解有向图中两点间最大距离的问题来实现的。

对于单条馈线的拓扑，确定两点间最大距离即是确定最长单条馈线及其起、止点的X轴坐标，这条最长的路径被定义为主干线。对于两两变电站间的拓扑，确定两点间最大距离即是确定所有馈线中最长馈线的起、止点的X轴坐标，在此基础上可确定各线中所有设备的X轴坐标。对于所有变电站间的拓扑布局，确定两点间最大距离即是确定相隔最远的两变电站的X轴坐标，进而确定中间各变电站在最终图纸中的X轴坐标。

定义无任何前驱的点为初始点，初始点的入度为0，无任何后继的点为终止点，终止点的出度为0[14]。DFS从每个初始点开始按照设定方向遍历到图中所有可达到的终止点，不断进行深度优先搜索的递归调用，直到找到某个给定初始点到给定终止点的最大距离[15]。

1.3 避免交叉的布局优化算法

避免交叉的布局优化算法用于确定配电网所有设备在最终拓扑图中的Y轴坐标。结合前述设备的X轴坐标，即可确定所有设备在图纸中的位置。

确定设备的Y轴坐标，可以通过将两两变电站间的布局数组插入所有变电站间的布局数组中，以形成全网布局数组的方式来实现。步骤如下：

1）确定全网拓扑接线图的大小(行数和列数)。以共有9个变电站(V0,V1,…,V8)的配电网为例，所有变电站间的拓扑布局数组如图1所示。将两两变电站间的布局数组的行、列信息填充到所有变电站间的布局数组中，便得到如图2所示的配电网全网的布局数组。

图1 9个变电站间的拓扑布局数组 Fig. 1 Topology layout array of 9 substations

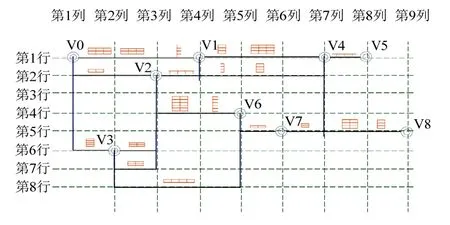
图2 9个变电站的全网布局数组 Fig. 2 Distribution network layout array of 9 substations

按照以下方法统计出配电网全网拓扑接线图所占用的总行数和总列数：①统计图2数组的第1行中有连接关系的所有相邻2列的布局数组(即两两变电站间的布局数组)的行数(每条主干线和分支线分别占一行)，可得到第1行中所有列之间 的行数R1,R2,…,Rn-1，那么第1行的总行数为max(R1,R2,…,Rn-1)=RL1，以此类推，统计出所有其他各行的总行数RL2,RL3,…,RLm，即可得到全网拓扑接线图需要占用的总行数R=RL1+RL2+…+RLm；②统计图2数组的第1、2列对应的各行中有连接关系的所有相邻2行的布局数组的列数(开关、变压器和变电站各占一列)，可得到各行的第1、2列之间的列数分别为L1,L2,…,Lp-1，那么第1、2列的总列数为max(L1,L2,…,Lp-1)=LR1，以此类推，统计骨架布局中所有其余相邻2列的两变电站之间的总列数LR2,LR3,…,LRn-1，即可得到整个拓扑接线图需要占用的列数L=LR1+LR2+…+LRn-1。

2）计算出每个设备的位置坐标。根据统计出的全网拓扑数组的行数R和列数L，可在A3或A4大小的图纸上计算出等间隔布置时每个设备的X轴和Y轴坐标，这样就实现了各变电站及各设备在图纸上不交叉的等距分布。

2 拓扑图自动生成算法的实现

2.1 数据预处理及单条馈线布局数组的生成

单条馈线的拓扑是配电网全网拓扑图实现的基础。首先根据DFS确定两点间最大距离所经过的路径为主干线，进而确定主干线的各个顶点，并使主干线顶点均匀分布；再继续遍历，确定各分支线及其顶点，使各分支线顶点等距分布，每条分支线与主干线各占一行；直到本条馈线上所有顶点的连接关系均体现出来为止。

2.1.1 生成拓扑图前的预处理

1）设备和连接的表示

单条馈线是以电源或变电站为起始点，以设备为终止点的线段。电源或变电站、开关、环网柜、柱上变等均用“顶点”表示，设备之间的连接关系用“边”表示。

2）数据预处理

数据预处理的主要功能有重复线段的删除、相交线段的判断及处理、顶点匹配、悬线处理等[16]。

重复线段是指2条线段之间的最大距离小于设定容差的线段。重复线段的删除应用于删除重复的架空或电缆线路。

相交线段的判断需要全面考虑各种相交情况。约定：①当点与线段的距离小于容差时，将其视为由实测或绘制时造成的误差，判定为相交，当大于容差时，判定为不相交；②当2条线段不相交时，计算它们的虚交点Q，若Q点在其中一条线段上，且Q点距离另一条线段近端点的距离小于容差，则将另一条线段延长至虚交点Q。相交线段的判断和处理应用于合并串、并联连接的导线设备。

顶点匹配是把一定容差范围内线段的端点作为一个顶点。约定：求解拟匹配点的平均坐标(包括X轴和Y轴坐标)，以此点为圆心，以一定的容差为半径画圆，将落在圆内的线段删除，以圆心为顶点，形成新的线段。顶点匹配应用于删除多余开关、环网柜等设备，仅保留其中一个。

悬线是指没有与周围的线段建立起关联关系的线段。悬线处理应用于删除不完整线路。

2.1.2 单条馈线布局数组的生成

运用DFS算法确定单条馈线的主干线及各分支线。运用DFS找到以节点V0为起点、V11为终点的最长有向路径P (V0,V1,V2,…,V11)，长度为11，如图3中蓝色线所示。各分支线的选取及节点顺序的确定与主干线类似，约定所有分支线均向右扩展。

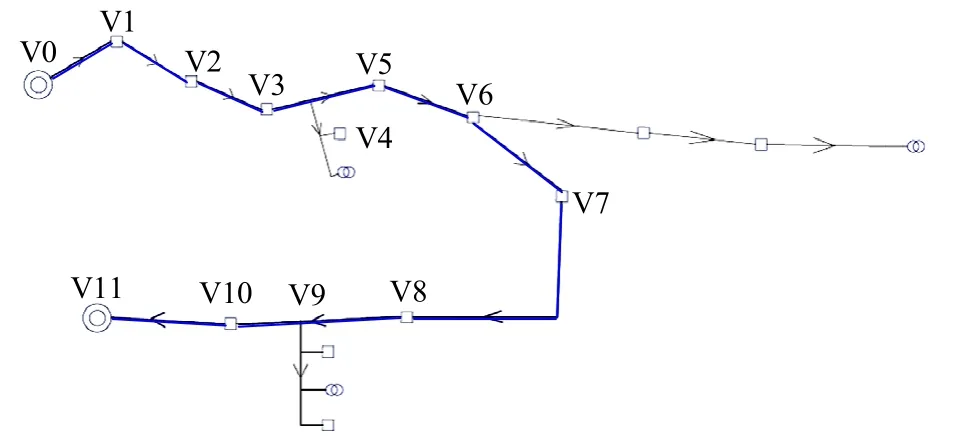
图3 从V0节点开始的最长路径排序 Fig. 3 Longest path sort from V0 node

按照上述规则和步骤读取并解析每条馈线的设备及其拓扑连接关系，将设备及其连接关系转化成单条馈线的布局数组，如图4所示。

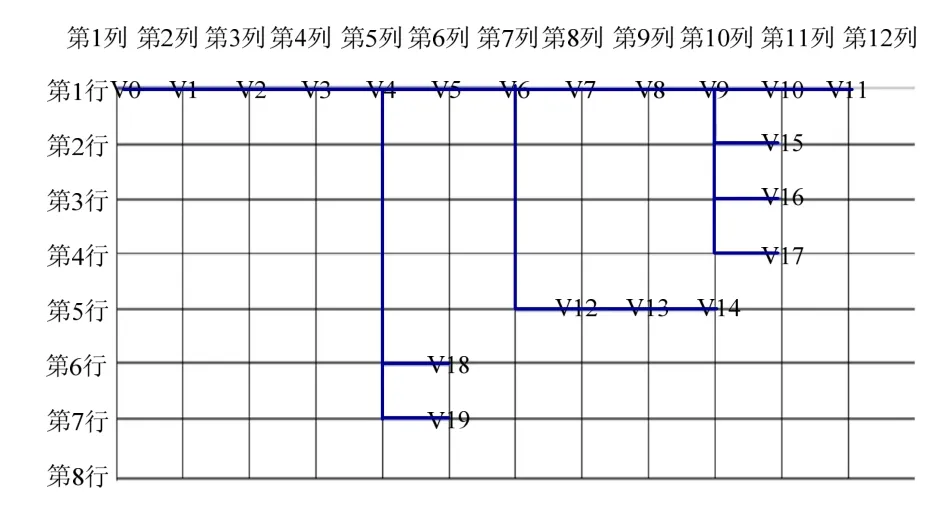
图4 单条馈线的布局数组 Fig. 4 Layout array of single line

各节点在布局数组中的行、列序号分别代表这个节点在拓扑图中的位置。根据馈线布局数组，可以很方便地得到馈线的拓扑图。

2.2 两两变电站间布局数组的生成

生成两两变电站间布局数组的步骤如下：

1）线段方向的修改。假定2条馈线的方向如图5(a)所示。经检查，不符合从左到右的方向假定，因此将线段方向进行如图5(b)所示的修改。

图5 各馈线方向的修改 Fig. 5 Direction modification of each line

2）找出两两变电站之间的所有馈线，合并起、止点，相关节点重新编号。2个变电站之间的馈线往往不止一条，需要找出两者之间的所有馈线，做到不重不漏。可保持节点较多的馈线中各节点的编号不变，将其他馈线的编号重新排列，形成新拓扑图，如图6所示。

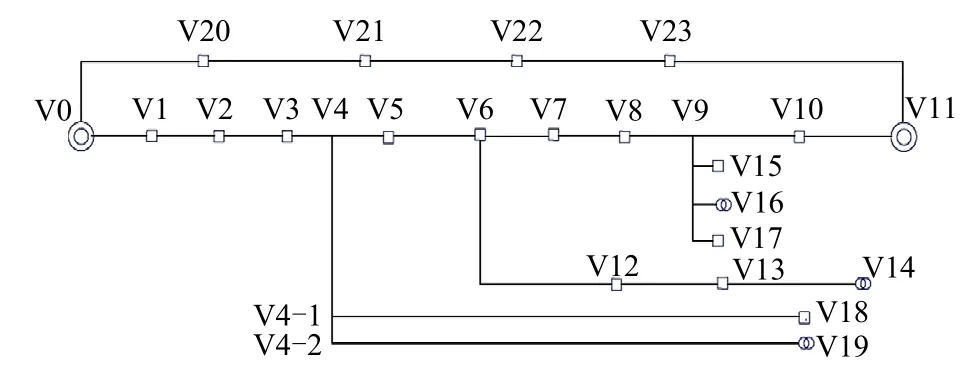
图6 两变电站之间2条馈线调整后的拓扑图 Fig. 6 Topological diagram of two lines between two substations after adjustment

3）确定两变电站间拓扑的布局数组。按照重新修改的线段方向和调整之后的顶点编号，根据DFS算法，得到两变电站间2条馈线的布局数组，

如图7所示。

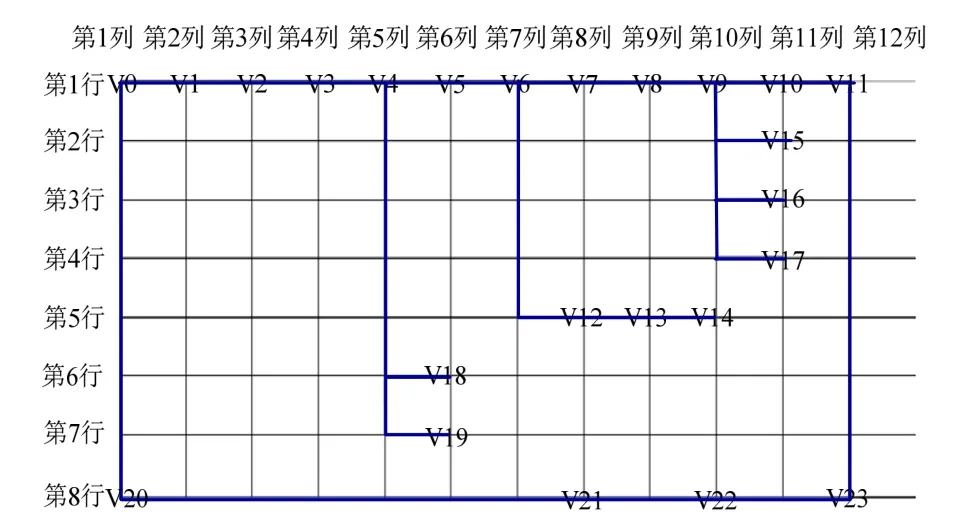
图7 两变电站间2条馈线的布局数组 Fig. 7 Layout array between two lines of two substations

如果两变电站之间的2条馈线有公共连接点，需要分情况进行处理，其中较难处理的情况有如下2种：

①交点在其中一条馈线的末端且有环路，如图8所示。图8(a)中的2条馈线在其中一条馈线分支线的末端V20处相交，且有环路。在这种情况下，可保持路径最长、设备最多的一条馈线不 动，本着使交叉点最少的原则，将环路信息放在布局数组的底部；调整之后的布局数组如图8(b)所示。 况下，考虑将环路信息放在布局数组的顶部，如图9(b)所示。

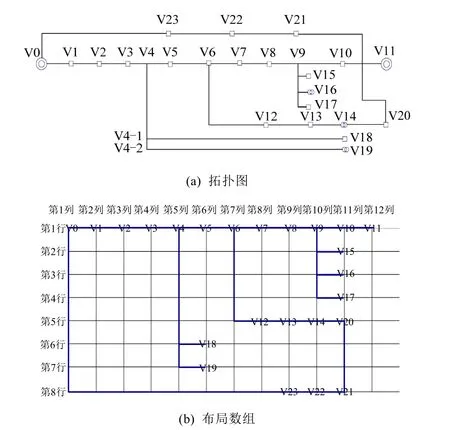
图8 两馈线末端有交点且有环路的情况 Fig. 8 Case that there is an intersection and a loop at the end of two lines

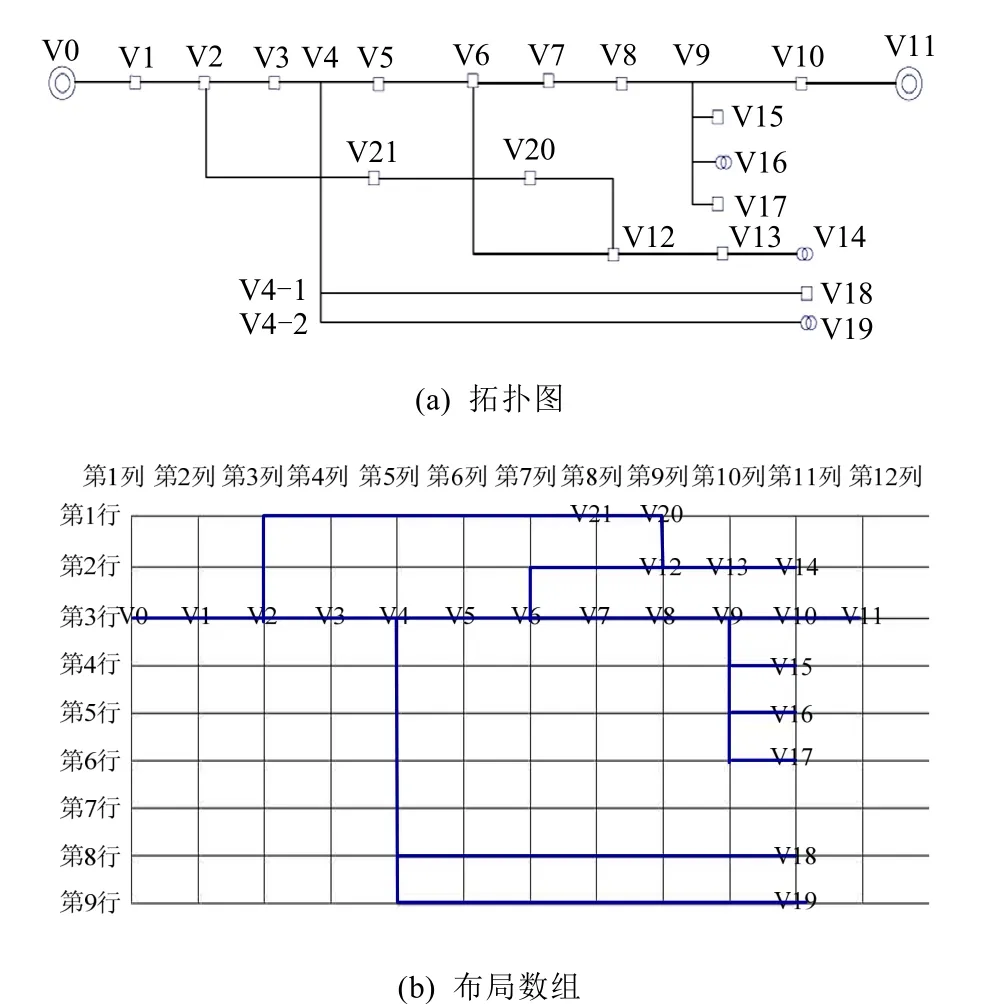
图9 两馈线中间有交点且有环路的情况 Fig. 9 Case that there is an intersection and a loop between two lines

2.3 所有变电站之间布局数组的生成

生成所有变电站之间布局数组的具体步骤 如下：

1）所有变电站间连接关系的确定。将所有发电厂、变电站及其连接关系全部体现在有向图中，如图10所示，规定线段的方向为从左至右。

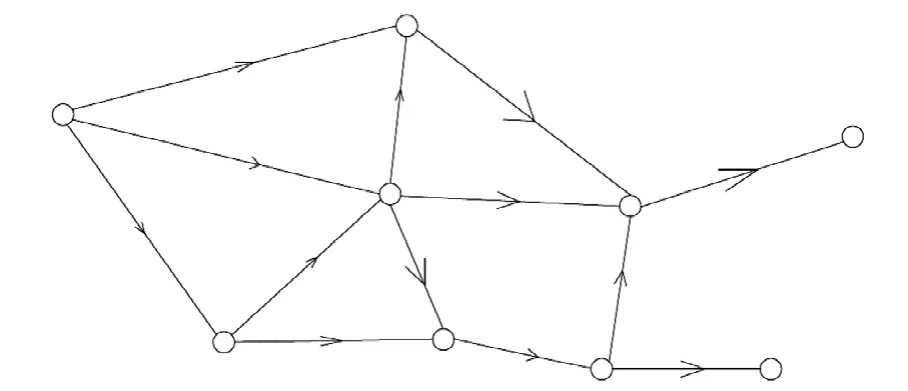
图10 所有变电站间布局图的方向定义 Fig. 10 Direction definition of layout of all substations

2）采用DFS算法求取变电站间的最大距离。以V0节点路径排序(如图11所示)为例，使用深度优先遍历，直到确定节点V0—V5的最长路径，从而可以确定节点V0—V5在二维数组中的位置。通过分析可知，二维数组中的行数和列数由各个节点的入度、出度和相互间的连接关系共同决定。

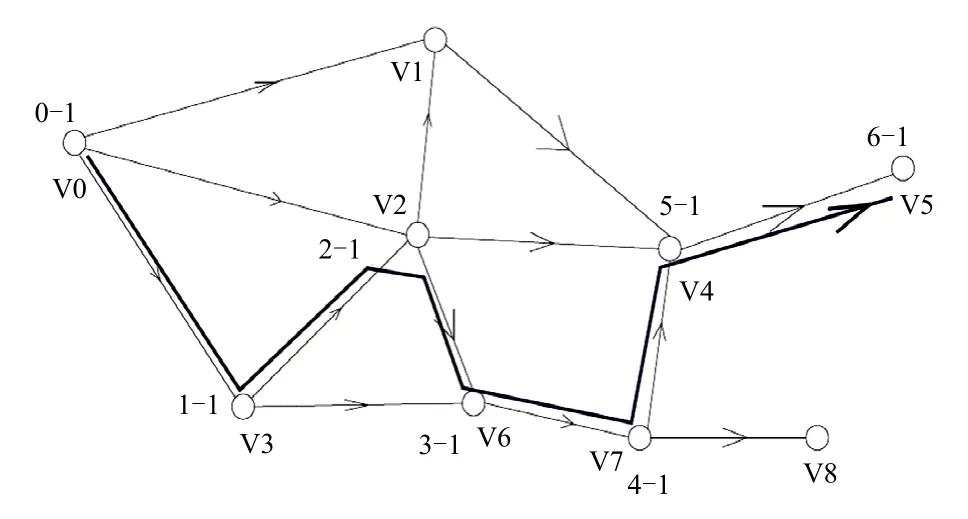
图11 V0—V5节点路径排序 Fig. 11 Path sorting from V0 node to V5 node

依照相同的方法，还可以确定图11中节点V0—V8的最长路径，从而得出节点V0—V8在二维数组中的位置。在所有初始节点到所有终端节点的最长路径确定后，综合起来便可确定所有节点在二维数组中的最终位置——所有变电站间的布局数组。图12即为图11中所有变电站间的布局数组。

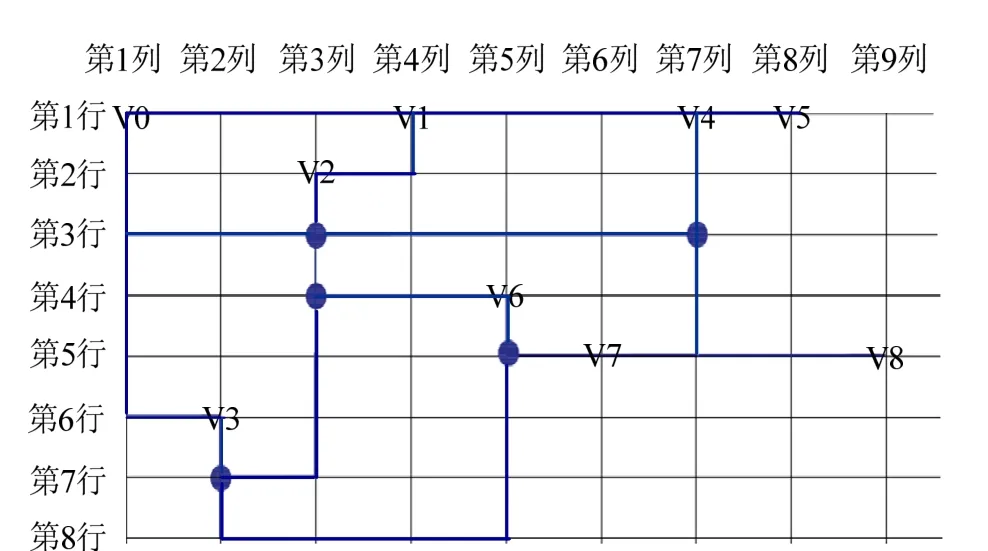
图12 各节点在二维数组中的位置 Fig. 12 Positions in a two-dimensional array of each node

2.4 配电网全网布局数组的生成

根据避免交叉的布局优化算法，可确定全网拓扑接线图的行数和列数。在A3大小的图纸上计算出拓扑图等间隔布置时每个设备的X轴和Y轴坐标，使各变电站及各设备在图纸上等距分布。

为简化起见，在图12所示的9节点(V0—V8)变电站间布局数组的基础上仅填充V0和V1两变电站间布局数组，从而生成配电网全网的布局数组，如图13所示。

图13 仅填充V0和V1两变电站信息的9个变电站的 配电网全网布局数组 Fig. 13 Distribution network layout array of 9 substations filled with only V0 and V1 substation information

2.5 配电网全网拓扑接线图的生成

根据上述求得的各变电站及各设备在图纸上的X、Y轴坐标值，即可在图纸上确定出各点(设备)的位置。

如果全网布局数组中某两点间存在相互连接，就在这两点之间生成一条边。将所有的互联关系均用边替代[17]，即可生成配电网全网的拓扑接线图。以图13所示的全网布局数组为例，对应生成的拓扑接线图如图14所示。

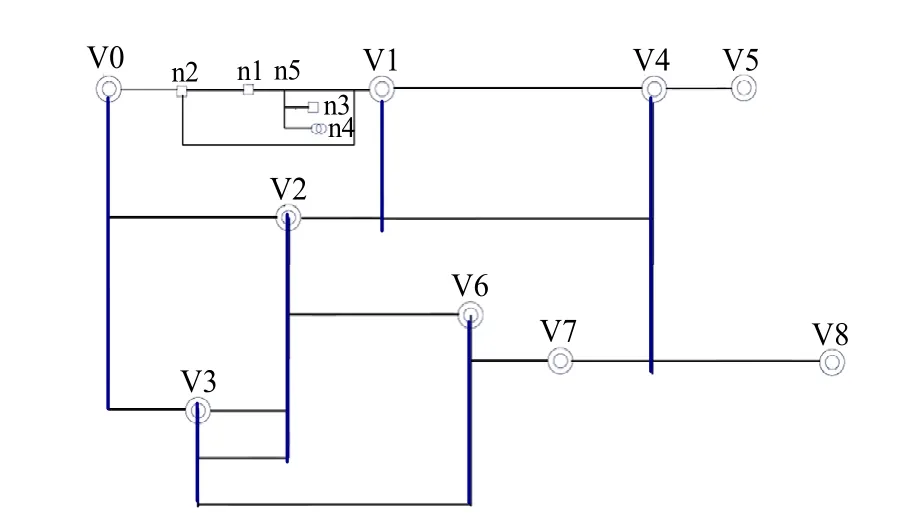
图14 仅填充V0和V1两变电站信息的9个变电站的 配电网全网的拓扑接线图 Fig. 14 Topology wiring diagram of distribution network of 9 substations filled with only V0 and V1 substation information

3 拓扑布线图自动生成算例

3.1 高压配电网拓扑布线图的实现

应用拓扑图自动生成算法对山东德州晶华网格2019年10 kV现状电网进行自动拓扑布线，其拓扑图如图15所示。本次绘图涉及变电站顶点20个，用时0.23 s。

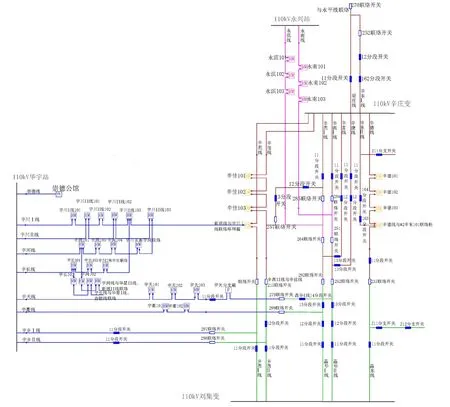
图15 德州晶华网格2019年10 kV现状电网拓扑图 Fig. 15 Topology of 10 kV power grid in Dezhou Jinghua in 2019

3.2 中压配电网拓扑布线图的实现

应用拓扑图自动生成算法对山东德州晶华网格远景年10 kV电网进行自动拓扑布线，其拓扑图如图16所示。本次绘图涉及变电站顶点44个，用时0.42 s。

图16 德州晶华网格远景年10 kV电网拓扑图 Fig. 16 Topology of 10 kV power grid in Dezhou Jinghua in future

4 结论

利用深度优先遍历算法，提出了基于分层布局思想的配电网拓扑图自动生成算法，该算法修正了遗传算法等需经多次迭代才能获得最优或次优解的问题，改进了退火算法等随着馈线和变电站数量增加而难以收敛的问题。通过对国网德州供电公司城市电网规划河东区晶华网格2019年10 kV现状电网、远景年10 kV电网进行自动拓扑布线，验证了该算法的正确性、快速性和普适性。该算法生成的拓扑图虽然能清晰、准确地反映线路之间的连接关系，但目前尚不能反映各条线路的相对地理位置。下一步，将考虑从兼顾电气拓扑连接和相对地理位置的角度改进自动拓扑布局的算法。