锂离子电池荷电状态与健康状态估计方法

李沂洹，李慷*, 余渐

（1．利兹大学电子电气工程学院，英国 利兹 LS2 9JT；2．苏格兰电力公司，英国 格拉斯哥 G2 5AD）

0 引言

为了应对全球气候变化与能源供应短缺，中国、欧盟、英国以及其他110多个国家承诺在未来30～40年内实现净零排放。交通和电力是温室气体排放的2个首要行业，电池储能技术的大规模应用可以促进交通运输的电气化和可再生能源的接入与消纳，从而在加速交通运输和电力行业实现碳中和的进程中发挥重要作用[1-2]。根据文 献[3]的报告，到2040年，预计行驶在路上的电动汽车总数将达到1.5亿～9亿辆，全球固定式储能累计装机容量预计将达到1 300 GW·h。电池储能作为其中的重要组成部分，随着电动车和电网储能规模的日益扩大，电池工作过程中的安全问题不可忽视。

与其他类型的电池相比，锂离子电池具有循环寿命长、能量密度大、额定电压高、自放电率低等显著优点，因此被广泛应用于电动汽车和大型储能装置中[4-6]。电池管理系统(battery management system，BMS)是保证电池组安全可靠高效运行的重要元件，其主要功能包括数据采集、状态估计、充放电控制、电池均衡、热管理等[7]。其中，准确实时的电池参数采集和内部状态估计为电池充放电控制、优化管理和维护提供重要依据，确保电池组在规定的安全范围内工作，及时发现异常情况并进行干预处理，提前排除安全隐患，进而延长电池寿命[8]。

电池荷电状态(state of charge，SOC)和电池健康状态(state of health，SOH)是电池系统中的2个重要参数，为电池安全保护、充放电控制、热管理等功能提供重要参考，因此精确及时地获得SOC和SOH信息对于提高电池寿命和使用安全至关重要。然而，作为电池的内部参数，SOC特别是SOH无法被直接且准确地测量，只能通过各种直接及间接方法的结合，找到其与测量信号(例如电压、电流、温度等)之间的非线性关系，进而对SOC/SOH进行准确估计。

本文将系统地回顾和总结目前主要的SOC和SOH估计方法，分析不同方法的优缺点，并结合实际情况，对未来SOC/SOH估计技术的发展进行展望。

1 电池SOC估计方法

1.1 电池SOC估计方法分类

SOC是反映电池当前可用容量占最大可用容量百分比的一个参数，计算公式为

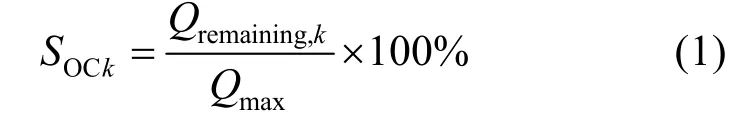
式中：SOCk为k时刻的SOC；Qremaining,k为k时刻的可释放容量；Qmax为当前循环下电池处于满充状态时可释放的最大容量，其数值随着电池的老化而减小。为了应用方便，通常使用电池额定容量作为Qmax的参考值，然而对于老化的电池，该简化并不适用，需要使用有效的SOH估计方法来更新Qmax的数值，否则会导致较大的SOC估计误差。

在不同SOC下电池储存能量的状态如图1所示，其中：100%表示电池完全充满电；0%表示电池完全放电；绿色部分表示存储的能量；空白部分表示可以重复充电；而红色部分表示由电池老化导致的永久损失。当电池还未老化时，红色部分不存在，即可以认为最大可用容量等于额定容量；随着电池的老化程度加深，红色失效部分的范围将会扩大，最大可用容量不断减小，此时要获得准确的SOC信息，需要首先对最大可用容量进行估计。

图1 不同SOC下电池能量存储状态 Fig. 1 Battery energy storage status under different SOC

由于电池工作状态复杂，起止状态通常未知，且SOC受到环境温度、电池老化、测量噪声等因素的影响，使得实时在线准确估计电池SOC具有一定困难。对此，国内外大量研究者对多种估计方法不断进行研究和改进，提出了许多应用于电池SOC估计的方法。常用的电池SOC估计方法可以分为直接法和间接法，如图2所示，直接法主要有库伦计数法和开路电压(open circuit voltage，OCV)法，间接法主要包括基于模型的方法和基于机器学习的方法。直接法中的库伦计数法也叫安时(Ah)积分法，该方法在计算SOC的过程中，传感器测量误差会导致SOC估计误差不断累积，且错误的初始SOC值会使估计结果偏离真实值[9]。而开路电压法需要将电池在无负载的情况下静置很长时间来测量OCV。因此，使用直接法来进行SOC的实时在线估计并不是一个好的选择，它们通常需要与基于模型的方法相结合，以实现更好的估计结果。

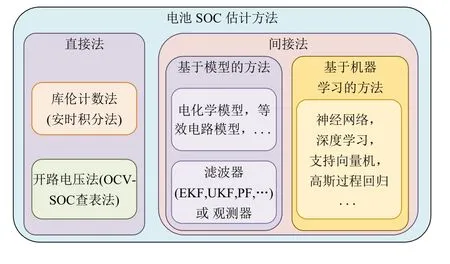
图2 电池SOC估计方法分类 Fig. 2 Categories of SOC estimation methods

基于模型的估计方法对电池模型的精度要求较高，而针对电池内部复杂的物理化学反应建立精确的模型并不容易。此外，基于模型的电池SOC估计通常与各种滤波算法、观测器等相结合，在使用中需要根据情况选择合适的模型参数，错误的参数选择会影响估计结果的准确性、收敛速度等。针对以上方法的局限性，机器学习方法作为一种应用简单、不需要了解系统先验知识且可以捕捉测量信号和SOC之间非线性关系的有效工具，被越来越多的学者应用到了电池SOC估计中。

1.2 库伦计数法

库伦计数法通过计算电池在充电/放电时测量电流对时间的积分来估计SOC[10]，计算公式为

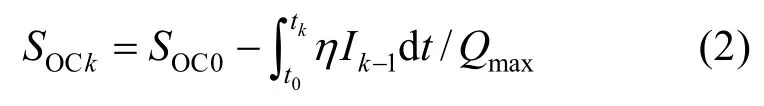
式中：t0为初始时刻；tk=t0+k×Δt，Δt为采样间隔；SOCk和SOC0分别为tk和t0时刻的SOC值；η为库伦效率；Ik-1为k-1时刻的电流。

库伦计数法是一种简单且直接的开环SOC计算方法[11]，但从公式(2)不难看出其存在以下缺点：1）错误的初始SOC信息SOC0会导致估计结果偏离真实值，而实际应用中，由于电池启停是随机的，其起始和终止状态通常无法确定，因此很难获得准确的SOC初始值；2）电流采集过程中的误差会由于积分计算而不断累积，导致SOC估计误差不断累积；3）电池老化或工作环境变化会导致电池最大可用容量Qmax发生变化，若不及时更新校准，会导致错误的SOC估计结果。

针对这些缺点，库伦计数法通常与其他技术结合使用，例如基于模型的SOC估计方法中，公式(2)和电池模型可以分别看作是状态空间模型的状态方程和测量方程，然后使用滤波算法或者观测器等闭环方法估计电池SOC，能够减轻或消除错误的初始值和测量噪声对估计结果的影响[12]。

1.3 开路电压法

OCV是电池在空载条件下的热力学平衡势，通过逐步测量不同SOC下的OCV，可以确定其与SOC的关系并建立OCV-SOC关系表[13]。也就是说，OCV法是一种查表法，根据测量到的OCV数据，通过查找离线建立的OCV- SOC关系表来推断电池SOC。

该方法的实际应用主要受到以下缺点的限制：1）不同电池的OCV-SOC关系是不同的，即便它们具有相同的材料和结构[14]，然而对每一块电池在每一个SOC下测量OCV是一个耗时的过程，因为测量OCV需要长时间静置电池以达到令人满意的平衡状态；2）该方法是一种开环估计方法，对测量误差和不确定性扰动敏感，有些种类的电池，特别是磷酸铁锂电池，在SOC中部区间的OCV曲线非常平缓，这意味着很小的OCV测量误差就可以导致很大的SOC估计误差[15]； 3）电池老化和工作温度等条件变化也会影响OCV和SOC之间的对应关系。因此，该方法更适合在实验室条件下使用，而不适合进行实时在线的SOC估计。

1.4 基于模型的SOC估计方法

基于模型的SOC估计方法的示意图如图3所示。实际电池系统和电池模型的输入可以是负载电流和环境温度等，在大多数情况下，实际测量参数包括终端电压等。基于模型的SOC估计方法的原理是：根据输入信号和状态空间模型的测量方程可以计算出测量信号的模型输出值，比较其与实际测量值以得到残差，然后滤波器或观测器将根据该残差信息来更新模型参数和系统状态，给出SOC估计结果。

图3 基于模型的SOC估计方法示意图 Fig. 3 Schematic diagram of model-based SOC estimation methods

在基于模型的SOC估计方法中，不同类型的电池模型，例如电化学模型、等效电路模型、黑箱模型等，通常与库伦计数法结合以构成状态空间模型，其中作为状态变量的SOC是连接状态方程和测量方程的桥梁。基于该状态空间模型，可以使用不同的滤波算法或观测器来实现电池SOC的闭环估计，常用的有滑膜观测器[16-17]、扩展卡尔曼滤波(extended Kalman filter，EKF)[18-19]、无迹卡尔曼滤波(unscented Kalman filter，UKF)[20-21]、H∞[22-23]滤波等。自适应卡尔曼滤波算法通过更新噪声协方差矩阵来提高对SOC的估计结果，例如文献[24]使用Maybeck估计器来更新过程噪声协方差矩阵，文献[25]使用Sage-Husa自适应卡尔曼滤波来更新过程和测量噪声协方差矩阵，文献[26]使用一种基于残差的自适应UKF来调整过程和测量噪声的协方差值，与EKF、UKF以及自适应EKF相比，自适应UKF可以提供更准确的SOC估计结果。此外，文献[27]使用粒子滤波估计SOC，且在此文献的实验分析中，粒子滤波与EKF具有相似的估计精度，但计算速度是EKF的6倍。文献[28]使用无迹粒子滤波来估计SOC，与EKF、UKF和普通粒子滤波相比，该方法具有更好的估计精度和鲁棒性。

作为一种闭环估计方法，基于模型的SOC估计方法因诸多优点而被广泛使用。它对初始SOC值不敏感，在模型足够精确的前提下，可以给出准确的在线SOC估计结果。然而，该方法对模型的精确度依赖性较强，但电池的工作特性呈现高度非线性，想要建立精确的电池模型并不容易，往往需要耗费大量的时间精力，有时还需要关于电池系统的先验知识。因此，该方法并不适用于所有种类的电池[29]。

1.5 基于机器学习的SOC估计方法

随着计算机技术的快速发展，越来越多的机器学习算法被用于电池SOC估计。人工神经网 络[30-31]、深度神经网络[32-33]、递归神经网络[34-35]、高斯过程回归[36-37]等算法，都可以直接建立测量信号(如电压、电流、表面温度等)与SOC的关系，基于测量信号直接估计电池SOC。

该方法的主要优点是不需要任何先验知识，在训练模型的过程中可以通过向模型加入其他输入来提高模型在各种不同操作条件下的性能，并且适用于所有类型的电池[38]。其主要问题是训练一个符合要求的模型往往需要大量且全面的训练数据，并且对于使用低成本微处理器的电池管理系统，需要注意最终模型的尺寸和计算复杂度不要超过限制。

2 电池SOH估计方法

2.1 电池SOH估计方法分类

SOH是用来评估电池老化或衰退程度的一个重要指标。该参数以百分比的形式表示当前电池相对于新电池的健康状态，新电池的SOH为100%。电池内部的化学反应和物理过程不可避免地会导致电池衰退，因此SOH随着电池使用时间的增加而不断降低。电池容量和内部阻抗是计算电池SOH的2个常用指标，根据对电池老化机理的研究，电池老化过程中容量的衰退主要是由锂存量损失和电极活性材料损失导致的[39]，而内部阻抗的增加主要是由固体电解质相界面膜的形成和成长导致的[40]。大多数研究使用实际容量来评估电池SOH，公式为

式中QN表示电池额定容量。通常来说，当电池实际最大可用容量下降到额定容量的80%时(即SOH=80%)，认为电池寿命终止并需要被更换。

由于电池内部反应机理复杂，有诸多导致其性能衰退的运行及环境因素，比如环境温度、运行中的放电深度、充/放电倍率等。且各种因素相互耦合，使得准确且快速地估计电池健康状态极具挑战。本文将目前常用的电池SOH估计方法分为基于模型的方法、基于增量容量分析(incremental capacity analysis，ICA)的方法以及基于机器学习的方法3类，如图4所示。其中，机器学习算法由于具有强大的特征提取和非线性拟合能力、广泛的适应性和应用简单等优势，在电池状态估计领域显示出越来越强大的应用潜力。

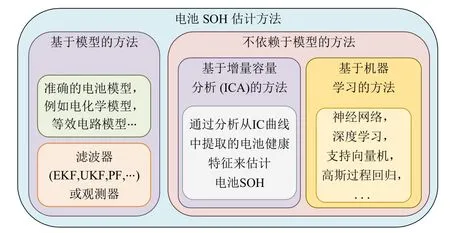
图4 电池SOH估计方法分类 Fig. 4 Categories of SOH estimation methods

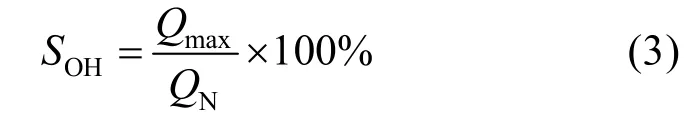
2.2 基于模型的SOH估计方法

在基于模型的电池SOH估计方法中，电池电化学模型、等效电路模型、经验模型等[41-44]通常与滤波器、观测器等结合使用，以实现在线容量估计。例如，文献[45]基于Thevenin模型，使用自适应H∞滤波器来估计电池容量。文献[46]从电化学模型中提取了5个与电池老化具有明显关系的特征参数来估计容量。文献[47]基于经验模型， 使用2个独立的EKF先后对Arrhenius老化模型的参数和电池容量进行估计。

在该方法中，能准确描述电池动态性能的电池模型是实现高精度SOH估计的基础。文献[48]详细总结了常用的电池模型，例如电化学模型、等效电路模型、黑箱模型等，并介绍了等效电路模型的结构选择和参数辨识方法。文献[49]基于二阶RC等效电路模型，对EKF、粒子滤波和递归最小二乘这3个算法在电池容量估计中的准确性和收敛速度等表现进行了比较和分析，结果表明：粒子滤波在电池老化的早期表现出最快的收敛速度和最好的估计结果，但长期表现最差且计算量最高，EKF的长期表现相对较好且计算负荷最小，而最小二乘算法在长期表现和计算量上都处于中间地位。

此外，考虑到电池SOH是一个缓慢变化的状态，而电池SOC及电池模型参数等通常快速变化，研究人员提出了多种多尺度估计框架分别在宏观尺度下估计电池SOH，并在微观尺度下估计电池SOC及辨识模型参数，例如多尺度EKF[50]、多尺度双H∞[51]、多尺度双自适应粒子滤波[52]等。

尽管该方法可以实现较为准确的电池SOH估计，在使用电化学模型时还可以给出较为清晰的电池内部微观反应过程，但其估计结果高度依赖于模型的质量。然而建立精确的电池模型并非易事，这需要对电池动态具有充分的了解以及大量的先验知识。此外，为了使模型性能不随电池老化而降低，需要在使用过程中不断更新模型的参数，模型中存在的大量参数使得计算负荷较重。

2.3 基于ICA的SOH估计方法

ICA法和差分电压分析(differential voltage analysis，DVA)法近几年来被广泛用于对电池容量衰退的评估。该方法的核心是增量容量(incremental capacity，IC)曲线及差分电压(differential voltage，DV)曲线。其中，IC曲线是电池容量对端电压的导数(即dQ/dV)与端电压V的关系曲线，而DV曲线则是端电压对容量的导数(dV/dQ)相对于容量Q的变化趋势[53]。IC曲线通过微分操作，将电压曲线上平台区的微小变化巧妙放大，转换为便于观察和分析的波峰。通过对IC曲线波峰的幅值、位置、形状、面积等特征进行分析，可以推断电池老化的模式和机理，从而估计电池的SOH[54]。例如，文献[55]在IC曲线上观察到5个不同的特征，通过分析这5个特征随电池老化的变化，最终选定与SOH有明显关系的2个波峰和1个波谷来估计SOH。文献[56]根据电压与SOC在不同老化程度下的关系，得到了dQ/dV及dV/dQ与SOC的关系曲线，将传统的基于电压的IC及DV曲线转换为基于SOC的IC及DV曲线，并从中提取了3个易于识别的SOC位置来估计电池SOC和实际容量。文献[57]以IC曲线上波峰所对应的电压为中心，根据给定的电压变化量可以确定该电压区间的起止时间点，由此可以计算出该区间对应的容量变化量，并依据该容量变化量与电池SOH之间明显的线性关系来在线估计SOH。

为了从IC曲线上获得这些与电池老化有明显关系的特征，电池需要在一定的电压或SOC范围内工作。例如，在文献[55]中，电池充电的起始SOC不得高于60%，否则将无法观察到选定的特征。此外，ICA/DVA方法要求充放电电流较小以确保电芯接近平衡状态[58]，对测量噪声敏感，易受到操作温度的影响，这些缺点限制了该方法的实际应用。

2.4 基于机器学习的SOH估计方法

复杂的电池内部反应和不确定的工作条件使得基于模型的和基于ICA的电池SOH估计方法都具有一定的局限性。近年来，随着大数据、云平台等新技术的发展，机器学习算法在电池SOH估计领域展现出巨大的潜力。该方法不需要有关电池复杂内部反应原理的先验知识，且易于应用。高斯过程回归(Gaussian process regression，GPR)[59]、核岭回归(kernel ridge regression，KRR)[60]、支持向量机(support vector machine，SVM)[61]、随机森林回归[62]等机器学习算法已成功用于电池SOH估计。GPR可以同时估计电池容量并量化估计结果的不确定性[63]。文献[64]从部分IC曲线上提取了11个健康特征，并以这些特征作为GPR模型的输入建立了电池退化模型，实现电池SOH估计，该模型的精度和鲁棒性在NASA电池老化数据集的4块电池上得到验证；其缺点是，作为输入的健康特征对不同类型的电池来说是不同的，需要重新选择并训练模型。文献[65]基于灰色关联分析从电池的充电曲线中提取了8个健康特征，以这些健康特征为输入、电池容量为输出训练相关向量机(relevance vector machine，RVM)模型。这些方法的估计结果在很大程度上取决于人为提取的特征参数是否能准确描述电池衰退趋势，但特征的人为提取过程往往会带来很大的工作量。此外，由于所提取的特征通常只适用于特定应用(电池类型、工作条件等)，因而模型不具有普适性和概括性。

针对这一问题，Elman神经网络、长短期记忆(long short-term memory，LSTM)、卷积神经网络(convolutional neural network，CNN)等可以自动从测量信号中提取特征的技术在SOH估计中的应用得到了广泛研究。文献[66]使用电池过去循环的充电容量作为Elman神经网络的输入来实时预测电池接下来的循环中的容量。文献[67]使用LSTM网络来估计电池容量，仅以电池电压、电流等测量信号作为输入，并且该方法的鲁棒性和灵活性在模拟的电动车不同行驶模式下采集到的电池数据集上得到验证。文献[68]直接使用一个循环中部分充电段的电压、电流和对应的累积容量作为卷积神经网络的输入来估计电池容量。这些方法选择了电压、电流等直接且易于获取的参数作为模型输入，而不需要费时费力的人为特征提取过程，这使得它们的应用更为简单方便。然而，这些方法的估计结果对数据的依赖性很高，只有足够的训练数据集才能训练出各方面性能令人满意的模型。

文献[69]比较了用于电池容量估计的3种不同神经网络的表现，即前馈神经网络、LSTM和CNN，实验结果表明：在可用电池老化数据有限的情况下，这些模型很难给出令人满意的估计结果。显然，基于机器学习的方法在电池容量估计中显示出了巨大的潜力，但其性能在很大程度上取决于训练数据集的大小。然而，收集大量的电池退化数据需要大量的循环测试，这一过程非常耗时且成本高。为此，研究人员将迁移学习的概念与这些方法相结合，以提高它们在小数据集上的性能。例如，文献[60,70-71]分别将核岭回归、LSTM和CNN与迁移学习相结合，提高了模型在小数据集上的电池容量估计精度。文献[71]考虑到CNN网络的尺寸和存在的大量冗余参数，除迁移学习外，还结合了网络剪枝技术，大大减小了最终模型的大小和计算量。

总体而言，与其他方法相比，基于机器学习的SOH估计方法适用于各种不同的充放电策略，对电池充放电电流、工作温度等没有限制，不要求电池完全充放电，且不需要对电池系统的深入了解。而其主要缺点是对数据集的依赖，以及相对较高的计算复杂度。在电池数据越来越丰富的应用场景下，基于机器学习的方法具有广阔的应用前景。

3 结论

1）由于对初始化误差和扰动不敏感、精确度较高、硬件设备易于实现等优点，基于模型的估计方法是当前最受欢迎的电池状态估计方法之一，但该方法对模型的依赖、模型对先验知识的要求、模型中大量参数随工况的变化等在一定程度上阻碍了其大规模应用。

2）基于机器学习的估计方法由于其自动的特征提取功能、强大的非线性拟合能力和表达能力、应用简单等优点，在电池状态估计领域展现了巨大的潜力。基于大量的电池实验建立丰富全面的数据库后，机器学习方法就能够建立充分描述电池在各种工作状态、环境下动态特性的电池模型，实现准确的电池状态估计。

3）针对机器学习算法在电池状态估计中计算量相对较大，对训练数据的样本数量要求较高，实际应用受到电池管理系统硬件、数据存储技术等限制的问题，提出以下解决方案：①从算法角度上，可以将现有算法与新算法相结合，利用新算法、新技术弥补现有算法的不足，例如可以结合网络剪枝技术来压缩、优化模型以去除冗余结构，进而降低内存和计算消耗，可以结合迁移学习技术，减小对大量数据的依赖等；②从硬件角度上，传感器的发展将会提高测量精度，减小测量误差对状态估计的影响，集成电路的发展将会不断提高算力，降低对模型大小和计算复杂度的要求；③随着云平台、大数据技术的不断发展，云存储、云计算等技术使得大量数据的收集与处理成为可能。多个方面结合发展将一起为机器学习算法在电池状态估计中的应用提供强大支撑，推动其实际应用。

致 谢

本文工作是在SP Energy Networks公司“A holistic approach for power system monitoring to support DSO transition”项目资助下完成的，在此表示衷心的感谢。