隧道口正馈线绝缘距离的理论计算及分析
2020-05-05
(中铁工程设计咨询集团有限公司,北京 100055)
0 概述
对于采用AT 供电方式的客运专线及高速铁路,正馈线一般在隧道外采用田野侧安装,在隧道内采用隧道顶部安装,并在隧道口第一根吊柱处对向下锚。因此,正馈线自田野侧向隧道内转换的过程中不可避免地要跨越承力索并穿过隧道口。该文主要以250 km/h 客运专线的一般设计参数为例,探讨正馈线与承力索、隧道顶绝缘距离的计算方法,并推求隧道口常用的技术参数取值对以上绝缘距离的影响。正馈线转换方式一般有2 种,通过H 型钢支柱转换(如图1 所示)、通过横梁转换(如图2 所示)[1]。这两种情况对于绝缘距离计算原理是相同的。

图1 隧道口横馈线通过硬横梁转换

图2 隧道口横馈线通过H 型钢柱转换
1 隧道口两处绝缘距离计算推导
1.1 计算条件
限于篇幅,该文计算做3 点假设。1)隧道口第一跨承力索按与线路中心重合考虑,正馈线与承力索交叉点按正馈线与线路中心交叉点计算。2)忽略隧道口第一跨承力索驰度,计算正馈线与承力索垂直高差按其与承力索座的垂直高差计算。3)忽略隧道口第一跨正馈线铠装护线条对正馈线曲线的影响。如进行精确计算时,则需以上因素的影响。
1.2 隧道口正馈线方程的推导
1.2.1 隧道口参数设定及坐标系的建立
隧道口正馈线平面布置如图3 所示。

图3 隧道口正馈线布置平面图
图3 中A 点:隧道外第一处正馈线悬挂点,A 水平面: A 点所在水平面;B’点:隧道内正馈线对向下锚点;C’点: 正馈线与承力索交叉点在A 水平面投影点;D’点: 正馈线与隧道口交叉点在A 水平面投影点;q:在A 水平面内垂直线路方向上,隧外正馈线悬挂点距承力索(线路中心)距离;p:在A 水平面内垂直线路方向上,隧内正馈线对锚点距承力索(线路中心)距离;n:在A 水平面内隧外第一根支柱距离隧道口顺线路方向距离;m:在A 水平面内隧道口距离正馈线对锚点顺线路方向距离。
在立面上,以A 点为原点在正馈线所在铅锤面内建立平面直角坐标系,x 轴正方向水平指向隧道口,y 轴正方向铅锤向上。
在图4 中,h:隧道内正馈线对锚点B’的y 轴坐标; h1:隧道内承力索高度的y 轴的坐标;h2:正馈线穿出隧道口处隧道口高度的y 轴坐标。
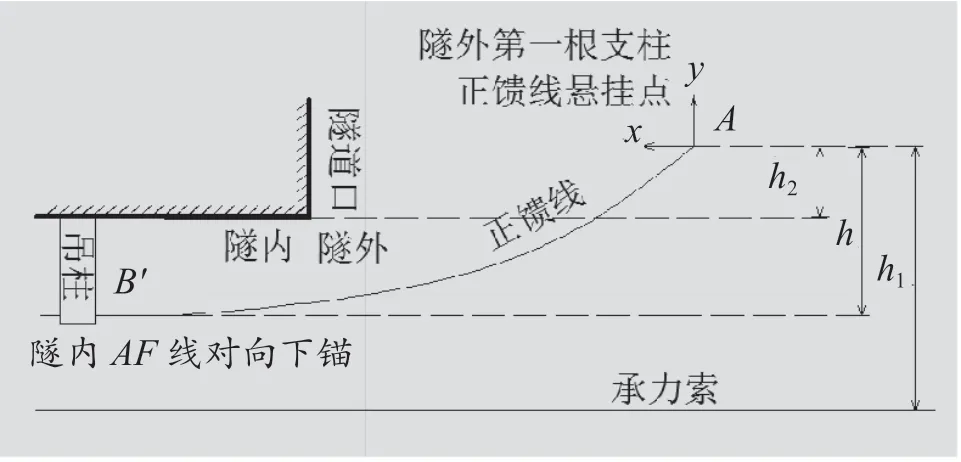
图4 隧道口正馈线立面布置(图3 EE 断面)
1.2.2 正馈线悬挂方程的推导
在上文坐标系内,推导AB’段正馈线的方程。
正馈线悬挂方程近似采用悬链曲线[2]:

x:正馈线上任一点x 轴坐标(单位m)。
y(x):正馈线上x 轴坐标为x 的点的y 轴坐标(单位m)。
T:导线张力(单位N)。
g:导线自重(单位N/m)。
L:L 为将AB’段导线从B’段延长至与A 点等高后的等效等高悬挂跨距(m),AB’段导线为此等高悬挂导线的一部分。

图5 L 取值示意图
在上文坐标系中,记AB 为AB’段正馈线在A 水平面内的投影长度。则正馈线曲线通过点A(0,0),B’(AB,h),将B(AB,h)代入式(1),并解方程得:

将(式2)代入(式1),即可解正馈线悬挂方程。

1.3 两处绝缘距离的计算推导
欲求在处承力索与正馈线交叉点处正馈线高度,则应首先求得C 点在x 轴上坐标,根据图3 所示,该点横坐标为(AC,0),AC 恰可近似采用下式表示,记


欲求在处隧道顶与正馈线交叉点处正馈线高度,则应首先求得D 点在坐标系x 轴上坐标,根据图3 所示,该点横坐标为(AD,0),AD 恰可近似采用下式表示,记


至此,推导出隧道口正馈线与承力索、隧道口绝缘距离的计算方法。根据电力牵引设计规范(TB10009—2016)要求,需保证在项目所处环境温度引起的张力变化范围内,均保证Δh1>540,Δh2>300。
2 隧道口技术参数对绝缘距离的影响
2.1 隧道口绝缘距离参数分析
从上文可知,正馈线悬挂曲线与m、n、p、q、h、h1、h2等数据相关,即使对于某一处特定工点,以上参数固定后,绝缘距离仍受导线张力T 影响,而导线张力受温度影响而实时变化。因此绝缘距离是一个受多参数综合影响、复杂、动态的变化过程。但详细探求参数组合,仍有特殊规律可以利用,以实现在任何工况下保证某项绝缘距离,达到简化设计,提高设备安全性的效果。该文以250 km/h 客运专线为例,举2 个例说明。
2.2 隧道口绝缘距离参数取值示例
根据一般250 km/h 客运专线隧道断面及接触网设计原则,参数取值做如下设定:
m:一般工程中为3 m~5 m,该文取3 m。
n:以平面布置图为准,该文取20 m。
p:根据隧内正馈线布置原则,取1.5 m。
q:按H 型钢柱柱顶向线路侧安装肩架V 拉悬挂正馈线,正馈线悬挂点距支柱内沿1.3 m,支柱侧面限界3.1 m,因此q 取1.8 m。
以轨面为0 高程,隧道内正馈线对向下锚吊柱一般长0.7 m,结合隧道净空,隧道内正馈线对锚点高程为8.1 m;经测量正馈线穿出隧道口处,隧道口高程8.54 m;承力索高程7.1 m;按隧道口采用10.7 m 高H 型钢柱,轨地高差0.45 m,绝缘子串长度按1 m,隧外正馈线悬挂点高程9.25 m。因此,h=-1.15,h1=-2.15,h2=-0.7。
2.3 隧外安装方案
2.3.1 特殊情况1:隧外第一根支柱距离隧道口较近时,宜采用隧内隧外正馈线等高方案
因隧道内正馈线安装高度已保证距隧道顶绝缘距离,如隧外正馈线悬挂点高度与隧道内正馈线安装高度相同,则跨中导线驰度低于两侧悬挂点,必能保证穿越隧道口时距隧道顶的绝缘距离,使其不受其他任何参数的影响。
但此方案要求正馈线跨距在保证正馈线转角不超标的前提下应尽量小。避免跨距较大时跨中正馈线驰度增大影响其与承力索交叉点处绝缘距离。例如,按2.1 中参数取值,降低隧道外正馈线安装高度至隧内对锚高度8.1 m,则h=0, h1=-1,h2=0.44。T 取对承力索与正馈线间距不利的2 000 N,根据上文公式绘制Δh1Δh2曲线,如图6 所示。
由图6 可见,n 值超过25 m 时,Δh1开始小于0.54 m,难以保证正馈线与承力索距离。

图6 隧内外正馈线等高时Δh1Δh2 曲线

图7 q 取值对Δh1Δh2 的影响
2.3.2 特殊情况2:宜采用隧外正馈线悬挂点位于承力索正上方方案
在2.1的参数配置中,绘制q取值从2 m~0 m的Δh1Δh2曲线,如图7 所示。
从图7 中可见,q 值对Δh1影响比较明显,q 值越小,对保证交叉点处正馈线与承力索间绝缘距离越有利。特别的,当q=0 时,即隧道外正馈线悬挂点正好位于承力索上方,此时正馈线与承力索的交叉点正好在二者各自的悬挂点,此时温度的变化对二者交叉点处的绝缘距离不会有任何影响。此方案是保证正馈线与承力索绝缘距离的极佳手段。
对于硬横跨方案,可通过调整硬横梁上AF 肩架的位置实现q=0,且对系统稳定性没有影响。因此可以看出硬横梁方案对比H 型钢柱方案的优势。
3 结语
该文针对隧道口正馈线的平立面布置,推导了用于计算正馈线与承力索、隧道顶绝缘距离的方法。同时提出了参数设置中的2 个特殊情况。限于篇幅,隧道口参数对绝缘距离的其他影响不能一一列举,例如,隧道口第一根支柱距离隧道口较远时,宜抬高隧外正馈线悬挂点以保证距承力索绝缘距离;隧内对向下锚吊柱较长对保证正馈线对隧道顶距离有利,但不利于保证对隧道内腕臂绝缘距离,等等。
隧道口绝缘距离受多参数影响,且同一个参数的变化对2 个绝缘距离的影响往往是相反的,因此参数取值需要综合考虑、寻取平衡。在设计过程中如能充分理解其变化规律,就能设计出可靠稳定的系统。
