基于模糊滑模控制的分数阶耦合系统同步研究
2021-10-17崔晓萌赵小山
崔晓萌,赵小山
(天津职业技术师范大学理学院,天津 300222)
近几年,分数阶微分方程相关理论具有良好的性能,因而在工程、金融经济、物理、疾病传播以及生物系统等领域应用广泛。如通过分数阶模型在断裂力学中的应用,Barpi 和Valente 改进断裂力学的裂缝扩展区域的微观力学模型,使其与分数阶流变模型结合[1];用分数阶微分方程描述电磁波和粘弹性体系来探索某些生物系统的行为[2]。由于其在安全通信和控制处理中的潜在应用[1],分数阶动力学系统及其相关现象中的混沌同步研究也日益受到关注[3-4]。分数阶混沌系统的同步问题首先由Deng 和Li 提出,之后他们以不同的方式研究了分数阶Chen 系统的混沌同步[4]。
目前,研究分数阶系统的同步有许多方法[5-7]。其中,滑模变结构控制方法在实际工程中逐渐得到各国学者的重视,这主要是因为该控制方法所设计的控制器结构是根据系统当前的状态,通过控制量的切换,使得系统状态沿着滑模面滑动,具有良好的鲁棒性。然而,在设计滑模面时,因不可避免地引入切换增益而导致了抖振的发生。为降低控制系统的抖振,Zhang等[8]发现模糊控制与滑模控制具有一定的相似性,并将这2 种控制方法结合,提出了模糊滑模控制,实现Duffing-Holmes 混沌系统的同步。许多学者应用模糊滑模控制方法研究不确定性,系统变量受约束的一些分数阶非线性系统同步问题[9-10],但是上述文献研究非线性控制问题只考虑了系统仅有不确定项或者外界干扰的一种情况。文献虽分析了模糊滑模控制方法研究驱动系统和响应系统同阶数的情况,但这些也仅是研究了驱动系统与响应系统是相同阶数的情况[11]。根据上述研究的基础,本文针对具有双重不确定性且具有不同阶数的分数阶耦合发电机系统,提出模糊终端滑模控制器的设计方法[12]。
1 预备知识
现今分数阶微分方程逐渐成为一种趋势,这是因为现实生活中的一些问题往往是复杂的,而传统的整数阶微分方程不能很好地体现研究对象随外界环境改变而变化的特点。分数阶微分方程具有遗传记忆性,在研究解决多变的模型时具有很好的优势。目前,对分数阶微分方程没有统一的一般表述,但是典型的定义有3 种,分别是R-L 定义、Caputo 定义、G-L 定义。由于Caputo 定义具有弱奇异性,因此在工程中用处广泛。
定义1Caputo 分数阶微分定义
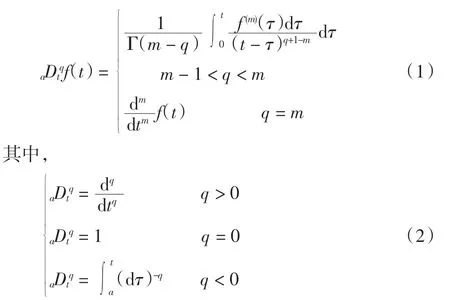
性质1分数阶微分满足
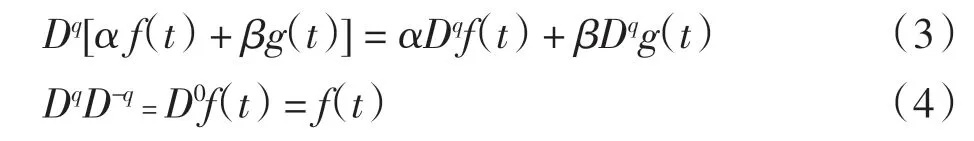
将自适应滑模控制理论与模糊逻辑系统结合[13],通过设计模糊滑模控制器降低系统的抖振现象。间接模糊滑模控制有成熟的设计步骤,但是这些步骤仅针对含有未知函数的系统,而对既含有未知项,又有外界干扰这2 种不确定分数阶系统的研究还不完善[14]。此外,现实生活中的系统往往复杂多变,故研究驱动系统与响应系统为不同阶数的情形具有极其重要的意义。
2 系统描述
2.1 分数阶耗损型耦合发电机系统的描述
根据一些研究学者的成果发现,耦合发电机系统是一种复杂的非线性动力系统,对该系统的参数特征以及动力特性进行研究,可为实际工程的发电机系统提供重要的实际意义。前人详细分析了整数阶耗损型变形耦合发电机混沌系统的动力学特性,在此基础上得到分数阶耗损型变形耦合发电机系统[15]。
分数阶耦合发电机系统为驱动系统,阶数为
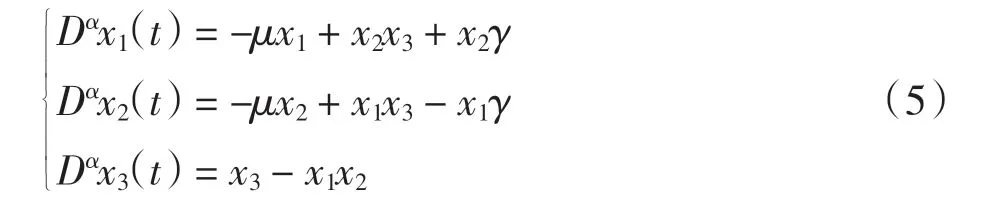
当参数分别为μ=2,γ=1,阶数α=0.95 时,出现混沌吸引子。分数阶耗损型耦合发电机系统为响应系统

式中:Δfi(y)为不确定因素;di(t)为外界干扰(外界干扰在数值仿真时采用高斯函数的形式,即Ei(t),故将原来式子放到了数值仿真处)。
为方便下文表述,将分数阶耦合系统中引入部分函数

2.2 误差系统的描述
由于驱动系统(5)与响应系统(6)的阶数不同,因此首先设计一个等效控制器U(x,y)={U1,U2,U3}∈R3×1,达到初步控制分数阶耗损型耦合发电机系统的目的。
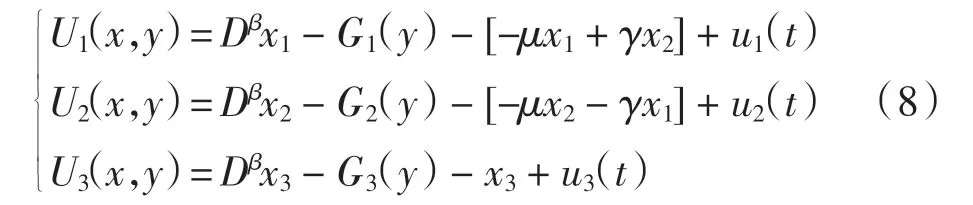
将式(7)和式(8)代入式(6)得到
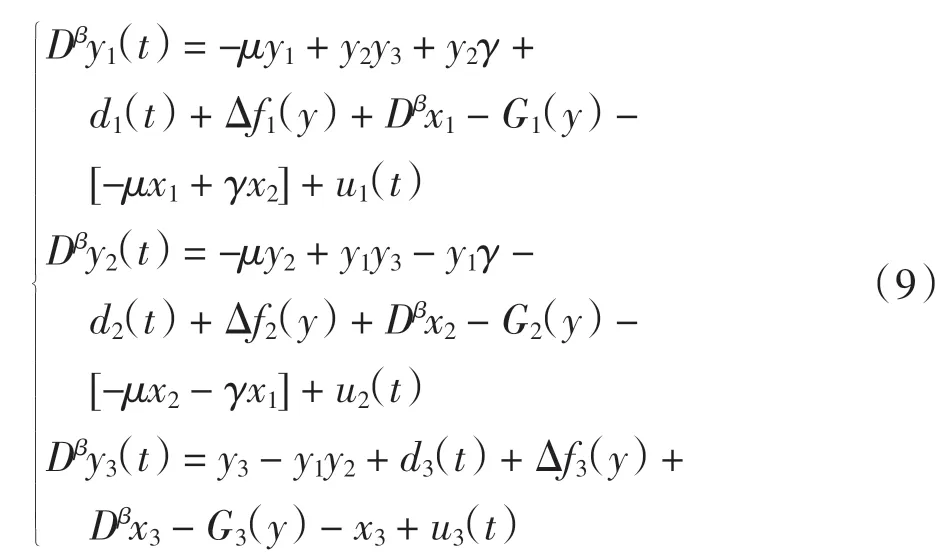
进一步化简
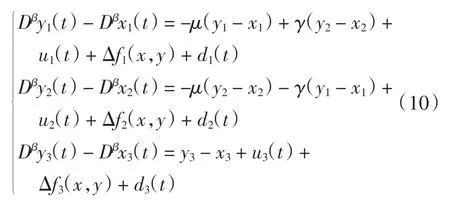
现给出误差系统定义[16]
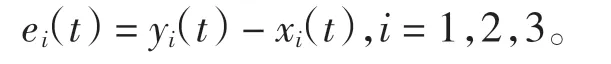
由式(10)得到驱动系统(5)和响应系统(6)的误差系统
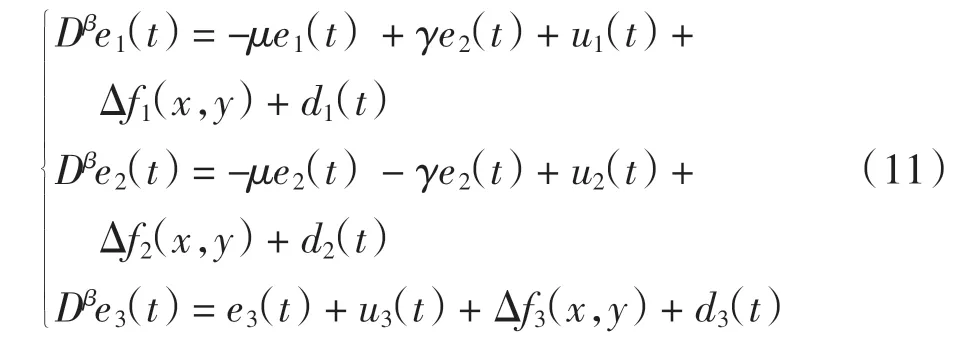
因此,针对式(11)设计合适的滑模面,使系统满足到达条件,不断调试对应的控制器u(t)=(u1(t),u2(t),u3(t)),使得双重不确定不同阶数的非线性分数阶系统趋于同步状态。
3 控制器的设计
3.1 滑模变结构控制器
为了后面的证明叙述方便,引入下面的假设以及定理[17]
假设1假设Δfi(x,y)和di(t)未知,并且满足
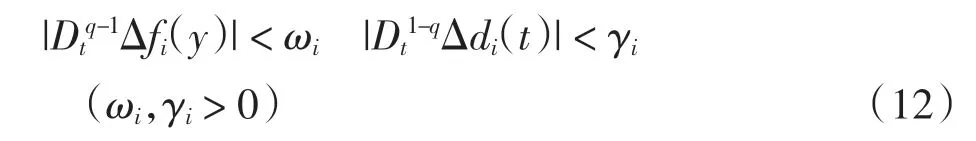
引理1设有实数a1,a2,a3,…,an,0<β<2。那么可以得到不等式
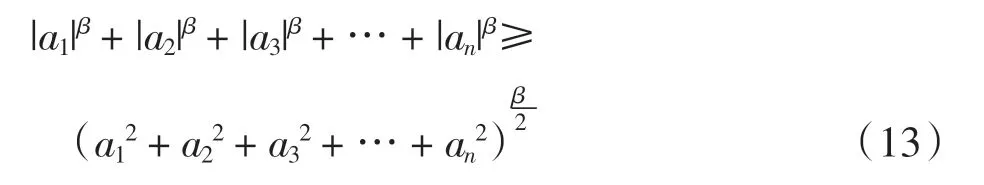
引理2假设存在连续正定函数V(t)满足微分不等式V(t)≤-pV(t)n,∀t≥t0,V(t0)≥0,式中p>0,0<δ <1 是2 个正常数。进而任意选择t0和满足条件的V(t0)可以得到
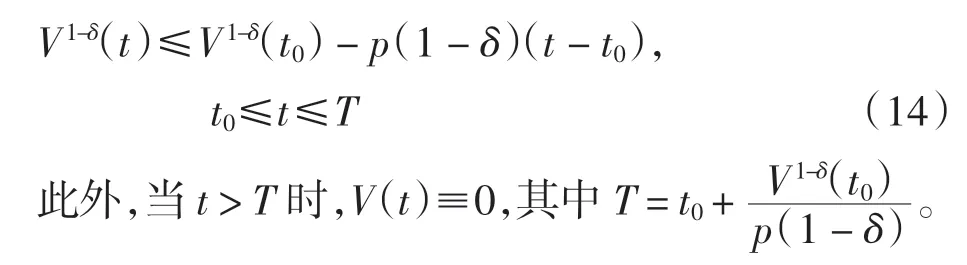
引理3分数阶微分方程Lyapunov 稳定性定理
对于一类分数阶非线性系统Dtax=f(x),x(0)=c,其中a∈(0,1]为分数阶算子的阶数。系统的平衡点x*为全局稳定的,如果在点x*的Jacobian 矩阵J=的所有特征值λj(j=1,2,…,n)满足下面条件|arg(λj)|>,j=1,2,…,n。
根据分数阶终端滑模控制理论及文献[18],设计非奇异滑模面
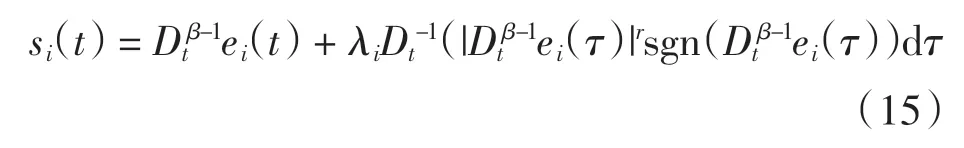
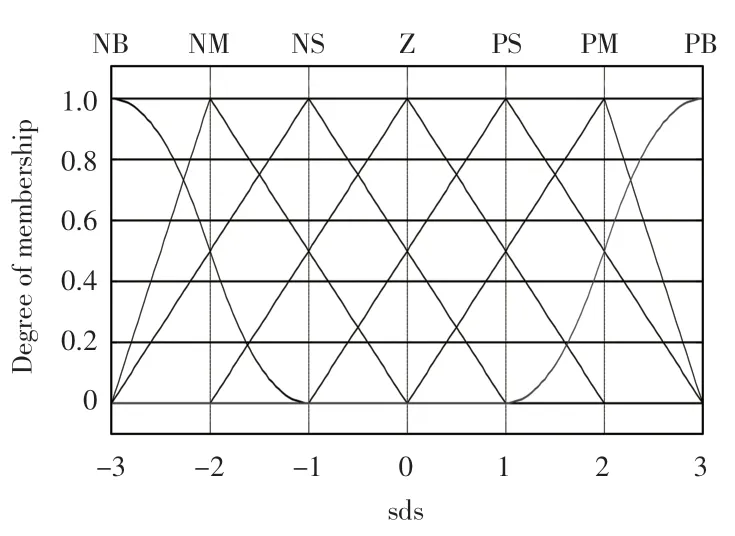
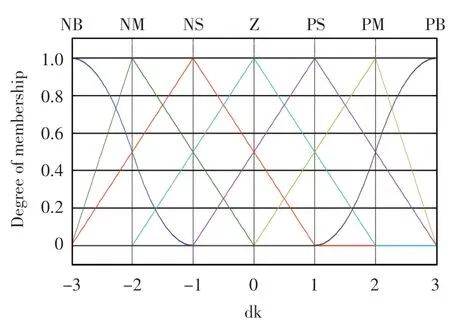
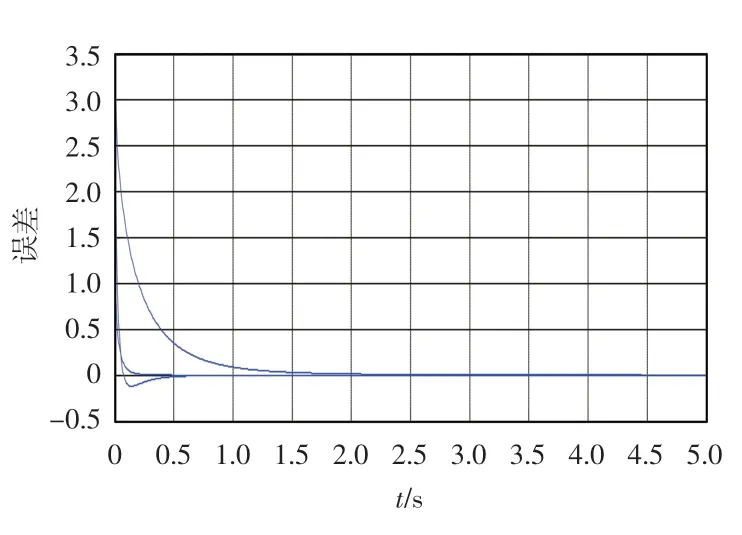
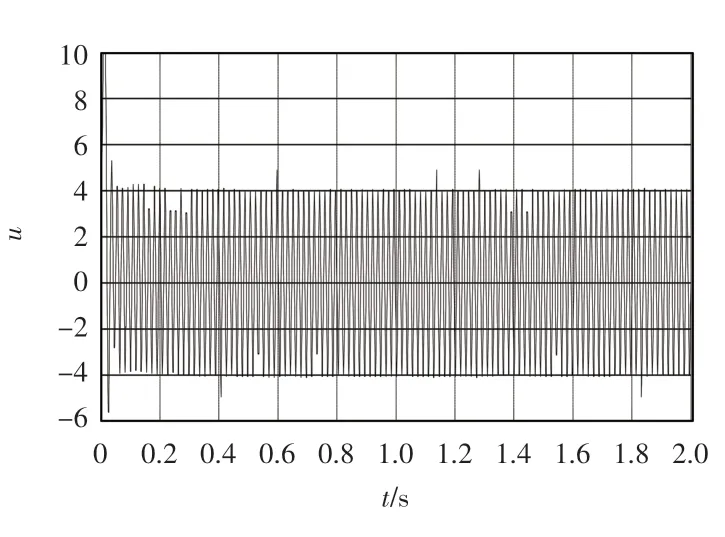
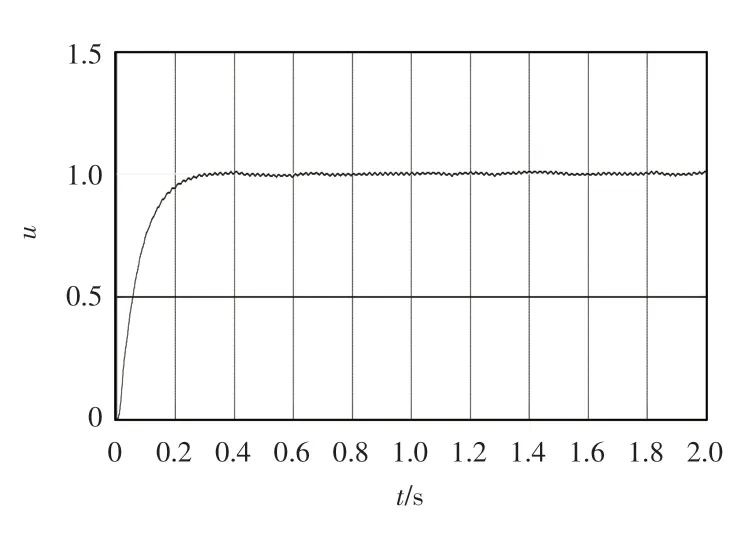
式中:0 定理1误差系统(12)在非奇异滑模面(14)上,系统的轨道在有限时间tδ内达到平衡点,其中 证明当系统发生滑模运动到达滑模面时满足si(t)=0,故 选取Lyapunov 函数 对式(16)求导 根据引理2 可以得出有限时间的上界。因此,当系统状态为到达滑模面时,其可以在有限时间内稳定到平衡点。 根据式(15)以及滑模控制理论设计理想的控制器u(t)=(u1(t),u2(t),u3(t))。其中,u(t)∈R1×3。 通过式(17)可以控制误差系统在有限时间内满足到达条件并趋于稳定,进而使得驱动系统(5)与响应系统(6)同步。当系统状态远离切换超平面时,上述控制器确保了系统能够快速稳定地到达滑模面[19]。根据Lyapunov 稳定性定理以及滑模控制理论进行验证。 证明 选取Lyapunov 函数 对式(18)求导得到 将式(11)代入 研究表明,无论误差系统的初始条件如何,其都能够满足滑模到达条件。即使在滑模面si=0 以外的情况,也能够在有限时间内到达或趋近滑模面[20]。根据Lyapunov 稳定性理论可知,误差系统式(11)稳定在平衡点,也就是实现了驱动系统与响应系统的同步。但因为设计控制器u(t)的过程中加入了切换增益Ki(t),这就不可避免地给系统的控制效果带来抖振,影响最终驱动系统和响应系统的同步效果[21]。 近几年,模糊逻辑控制系统相关理论逐渐趋于成熟。通过上述设计的滑模面s(t),运用模糊推理机制,最后去模糊化,将滑模控制与模糊控制结合,减少最初设计的控制器u(t)中切换增益和符号函数带来的不良影响,以达到优化改进的目的。 按照模糊逻辑控制系统的要求设计自适应模糊滑模控制器。 3.2.1 模糊化 模糊控制器的规则是基于专家知识或熟练的操作人员长期积累的经验。本文规定ss˙为模糊INPUT,ΔKi(t)为模糊OUTPUT。得到模糊集合为[22] 式中:NB 为负大;NM 为负中;NS 为负小;ZO 为0;PS为负小;PM 为正中;PB 为正大。 上述模糊集合的模糊输入以及模糊输出对应的隶属函数分别如图1 和图2 所示。 图1 sds 模糊输入隶属函数 图2 dk 模糊输出隶属函数 3.2.2 模糊规则库的建立 根据模糊规则库的规则对ss˙和ΔKi(t)进行模糊推理得 在控制器式(17)中,有一造成抖振的因素,即Ki(t)的值。Ki(t)的作用是为了补偿Ei(t),目的是为了使得滑模满足存在性条件。如若Ei(t)时变,Ki(t)也会时变。所以根据模糊逻辑控制系统,以专家经验实现Ki(t)的变化[24]。 为确保自适应模糊滑模控制器的设计有效保证误差系统的稳定,通过数值模拟仿真,检验控制器式(21)的有效性[25]。系统参数取μ=0.85,γ=0.17,λ1=1.92,λ2=2.87,λ3=4.73,r=0.6;对外界干扰di(t)采用高斯函数的形式,即取mj=5.0,nj=0.50。 设置系统初始值为y1(0)=0.98,y2(0)=1.37,y3(0)=2.01;x1(0)=1.96,x2(0)=0.89,x3(0)=3.22,自适应率=(0.18,0.74,0.95)。利用Matlab 和Simulink 进行数值仿真,得到误差系统随着时间的增加逐步趋于稳定,误差系统时间历程图如图3 所示。传统控制器时间历程图如图4 所示,模糊滑模控制器时间历程图如图5所示。 图3 误差系统时间历程图 图4 传统控制器时间历程图 图5 模糊滑模控制器时间历程图 图3 仿真结果表明,从任意初始条件出发的误差系统在控制器的作用下渐进稳定,进而实现驱动系统与响应系统之间的同步。 在未加入模糊逻辑系统时,传统意义下的滑模控制器因切换增益项带有抖振[22],图4 仿真结果表明,传统的滑模变结构控制器在运行时,因切换增益项而存在抖振,影响系统的同步性能。 为削弱抖振,根据模糊控制规则,改善控制器的性能。由图5 可知,根据专家经验,加入模糊控制系统后,增强了控制系统的鲁棒性,提高了传统控制系统在系统存在外界干扰和不确定情况下的适应性。 本文对分数阶混沌系统模糊滑模控制研究的现状进行了介绍,分析了目前该控制方法的研究中存在的缺点与不足,并研究了一类带有双重不确定项的分数阶耦合发电机系统的同步问题。通过设计模糊规则,根据滑模到达条件对切换增益进行有效估计。与现有文献设计的滑模控制器比较,本文设计能有效削弱抖振并且在有限时间内逐步趋于稳定。利用Lyapunov 稳定性理论证明了所改进的控制的合理性。但是,在模糊化和反模糊化时,仍缺乏系统的方法,主要是依靠专家系统的经验试凑。因此,建立完善统一的分数阶系统自适应模糊滑模控制理论以及实际仿真程序是下一步研究的重点。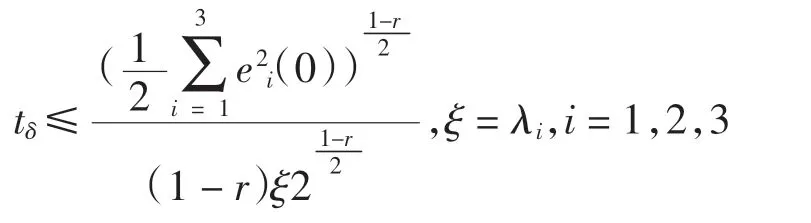
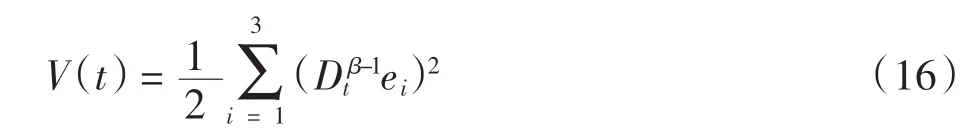
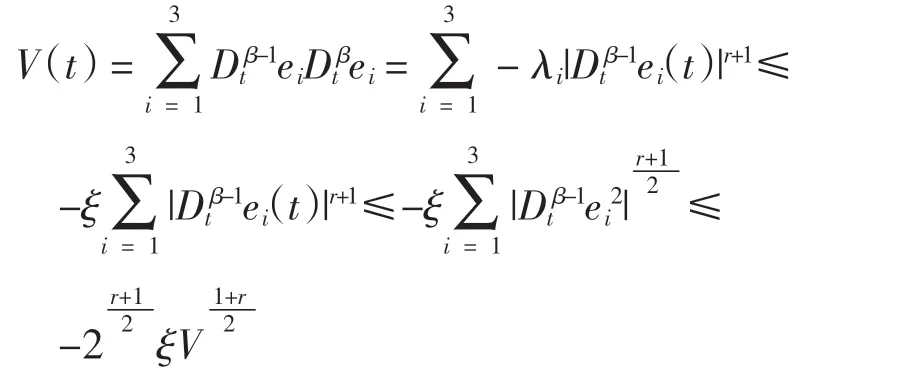

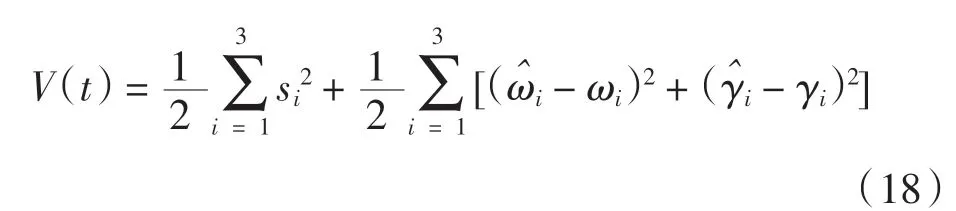
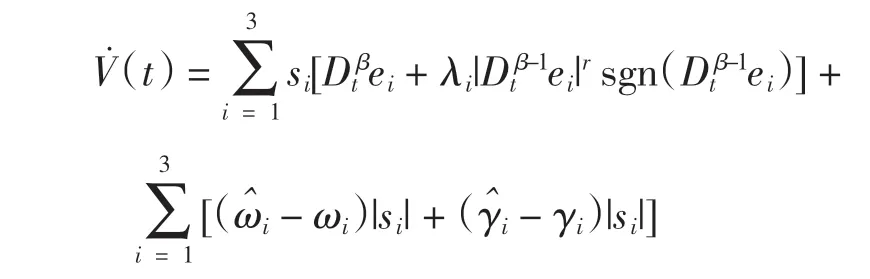
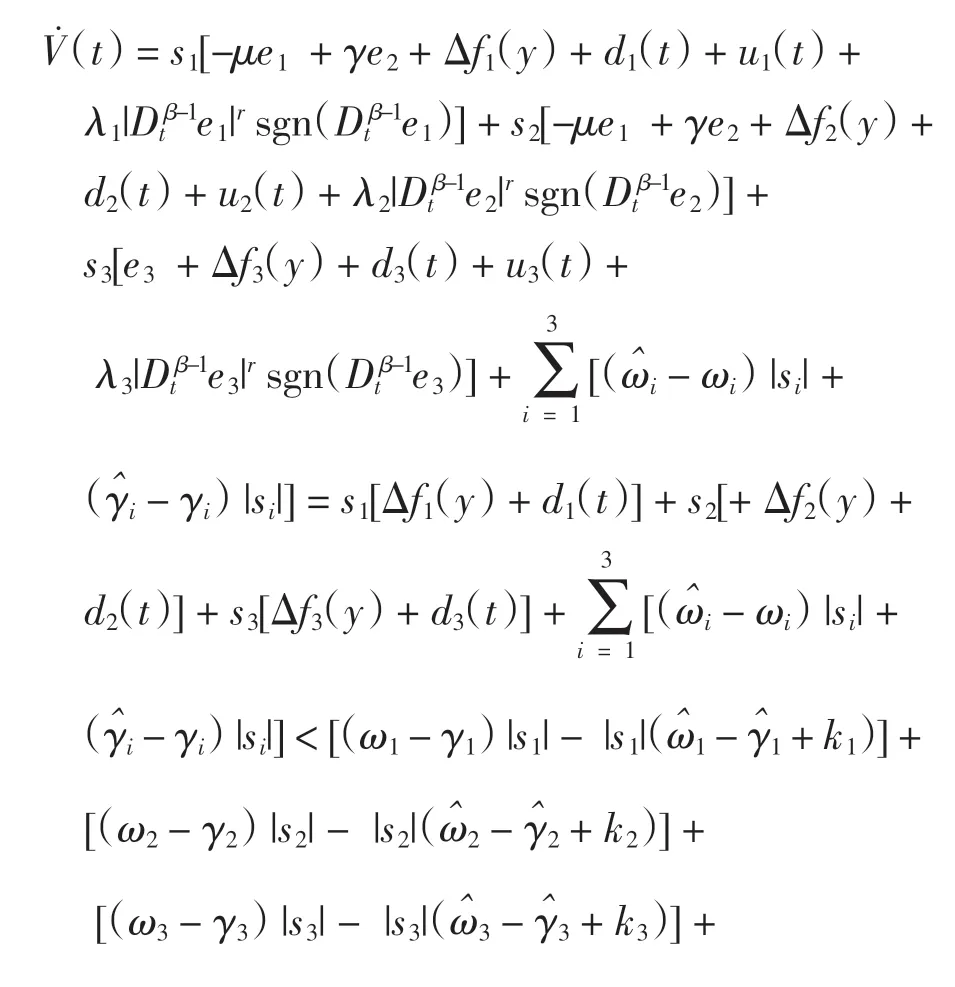
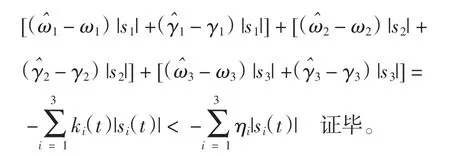
3.2 模糊滑模控制器



4 数值仿真
5 结语
