考虑铣削路径变化的平面薄壁件动态特性建模

姜颢天，靳 刚，阎 兵，李文硕

（天津职业技术师范大学机械工程学院，天津 300222）

薄壁件具有质量轻、结构紧凑、节约材料、强度高等诸多优点，已被广泛应用于航空航天等工业制造领域[1-2]。但是，薄壁件的加工过程中产生的铣削力会产生较大的变形和震颤[3-4]，导致国内目前只能采用保守的加工参数，且难以获得较好的质量[5]。平面薄壁件在加工过程中，切削点一直变化且不同切削点的动态特性不同，随着薄壁件的结构变化，整体的轻量化和工件形状越来越复杂[6]。研究平面薄壁件的不同切削点动态特性的变化规律，可以对薄壁件加工产生的振动进行有效地预测。

Shi 等[7]针对铣刀和工件的相对位置对薄壁件动态响应的影响，优化约束阻尼结构的参数以抑制薄壁件外层铣削过程中的加工振动的问题，提出了带有约束阻尼结构的薄壁件外层在动态切削力作用下的动力学方程。石佳昊[8]采用结构阻尼替代阻尼比的方式，分析了阻尼对系统动态特性的影响。Ren 等[9-10]在考虑薄壁铣削过程的动态特性的条件下，发现对于每阶模态，临界切割深度与振型的平方成反比。张广鹏等[11]对机床的整机动态特性进行了建模，实验结果表明应用均质梁、集中质量和结合部单元方法可以快速、准确地预测机床的动态特性。乔丕忠等[12]针对复合材料薄壁梁，构建了其本构关系，并对现有理论存在的问题进行了总结，根据不同方法得到控制微分方程并给出了相应的解析方法，对薄壁梁的稳定性问题进行了归纳。于福航[13]针对薄壁件加工过程中的稳定性问题，根据全离散算法建立了铣削动力学方程，并采用多步插值算法离散化时滞微分动力学方程中的时滞项，进行铣削稳定性预测算法的研究，并通过采用Matlab/GUI平台建立了薄壁件铣削稳定性预测及参数优化系统，对实际加工过程中薄壁件的切削稳定性进行了有效的预测。上述关于薄壁件切削的研究一般忽略随切削路径变化而时变的薄壁件动态特性，这势必会对研究结果产生影响。目前，模态分析已经有了较为成熟的理论和发展[14]，本文基于模态理论，通过锤击实验获得测试点模态参数，分析基于随着切削路径变化的平面薄壁件的动态特性变化规律，建立平面薄壁件模态参数预测模型，对平面薄壁件切削路径上各点的动态特性进行预测。

1 研究方案及理论建模

考虑到薄壁件的多模态及切削路径上刚度的时变特性，本文拟构建切削路径上有限点动态，并最终将其发展为可考虑全路径的统一模型。

实验研究方案可具体表述为：①基于模态理论，建立考虑铣削路径变化的平面薄壁件动态特性预测模型；②基于LMS 锤击实验，获得平面薄壁件若干个测试点的传递函数和模态参数；③根据实验结果对上述理论模型进行简化；④对实验所得的动态特性影响参数进行拟合，回代入理论模型得到最终的平面薄壁件模态参数预测模型；⑤根据预测模型和锤击实验对切削路径上不同于测试点的进行计算及试验，对比计算结果和试验结果，分析预测模型的有效性，并得出结论。

1.1 平面薄壁件动态特性模型

由于薄壁件的弱刚性特性，在切削加工过程中，系统结构的前若干阶模态都会对加工过程造成不同程度的影响。考虑结构阻尼，系统的多自由度动态方程可表示为

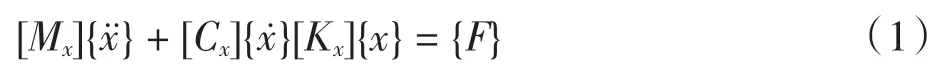
进行拉普拉斯变换，得到多自由度系统在s 域的运动方程

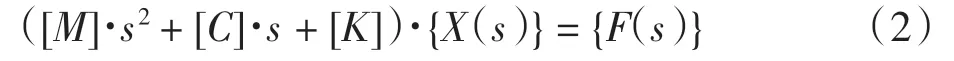
则多自由度系统的传递函数为

将式（3）展开为

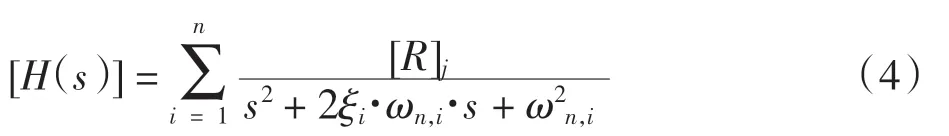
式中：n 维矩阵中每个元素[R]j=[α+βs]j代表第i 阶模态在矩阵中第a 行、第b 列的留数。根据Yusuf[15]的模态分析理论，可将式（4）展开为部分分式的形式

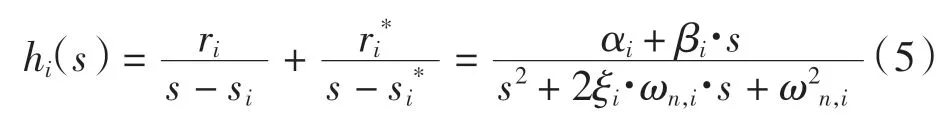
其中，ri、ri*为留数，

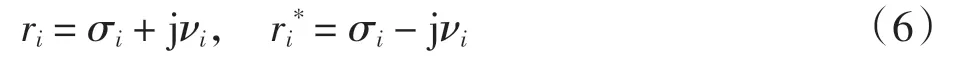
参数αi、βi为

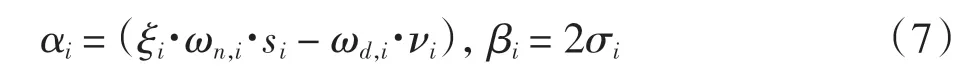
1.2 考虑铣削路径的平面薄壁件动态特性模型

在薄壁件铣削过程中，刀具将在工件表面作平移运动，而运动路径上工件的振动特性将随着切削点的变化而改变。若假设刀具相比于工件为完全刚性，则工件的振动完全取决于工件在该切削点上的动态特性。

若考虑工件切削路径的变化，方程（4）—（6）中ωi，n、ξ、ri、ri*、α、β 的值不再恒定，将变为关于路径的函数，即

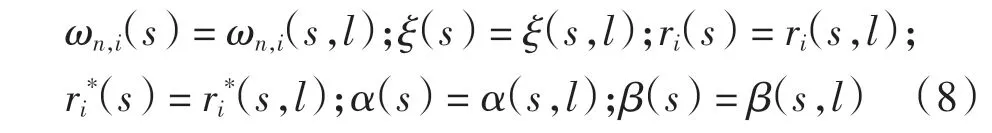
将式（8）代入式（5），得到随路径变化的不同高度和厚度的薄壁件传递函数

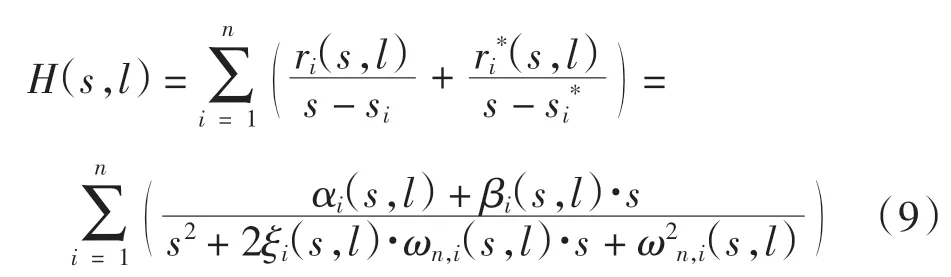
1.3 模型简化

在评估系统的动态特性时，考虑系统的若干阶模态是不现实且消耗巨大的，重点考察对系统动态特性影响较为显著的前几阶模态具有重要的现实意义。试验设备及工件如图1 所示。

图1 试验设备及工件

本研究主要采用单点激励单点响应的锤击试验方法，选择SERIAL#38264 传感器，C-ADAPTER 动态数据采集仪器，使用USB 接口与计算机连接通讯，如图2（a）、（b）和（c）所示。

实验所选的平面薄壁件如图2（d）所示，其悬伸处长宽高尺寸为180 mm×4 mm×90 mm，材料选取常用的铝合金6061。在锤击实验过程中，使用螺栓通过工件底板上的4 个通孔将工件固定在实验台上。

实验测试点从C1 点开始，沿工件长度方向每25 mm 建立一个测试点，直到右上角点C7 为最后一个测试点，7 个测试点位置如图2（d）所示。对平面薄壁件上7 个点粘贴传感器，并使用冲击锤在薄壁件另一侧进行锤击，如图2（e）所示，获得的系统前二阶模态参数（固有频率、阻尼和留数）如表1 所示。

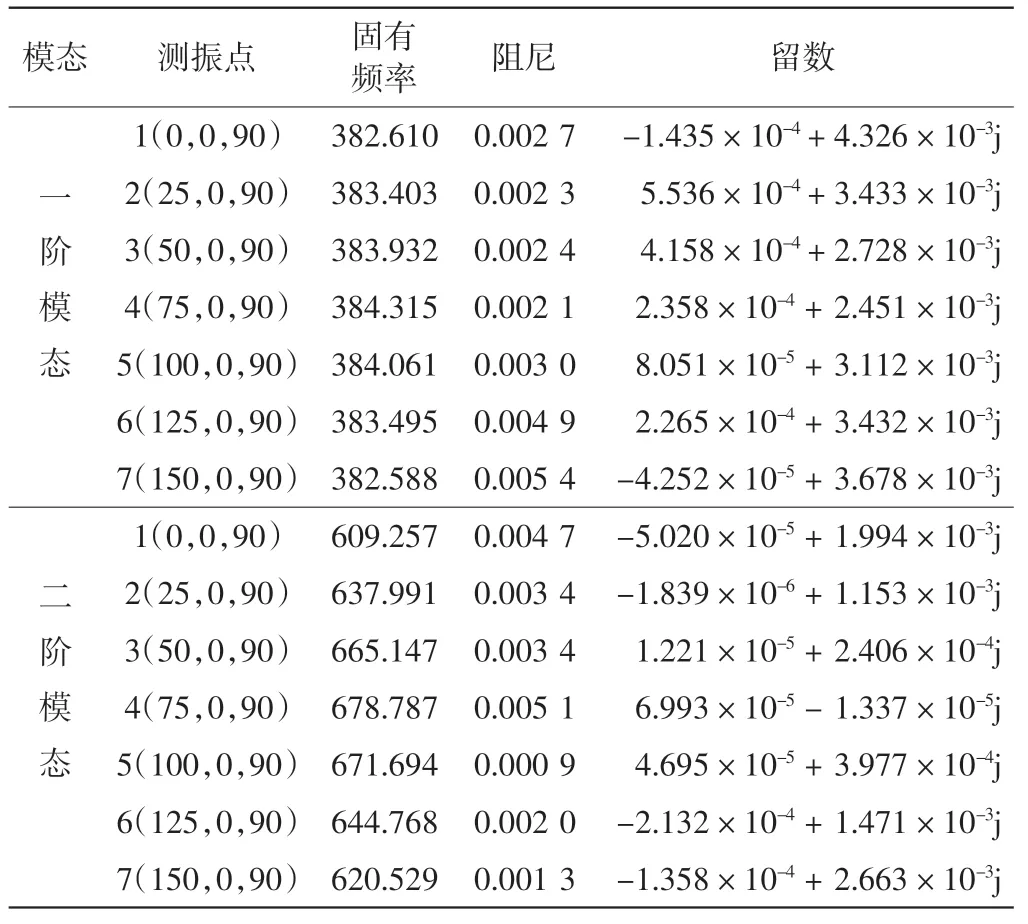
表1 高度90 mm×厚度4 mm 平面薄壁件的模态参数

基于表1 的实验数据和式（4），拟合获得了工件C1、C3、C5 和C7 四个点上的幅频响应曲线，平面薄壁件不同测试点的试验及仿真结果幅频图如图2 所示。

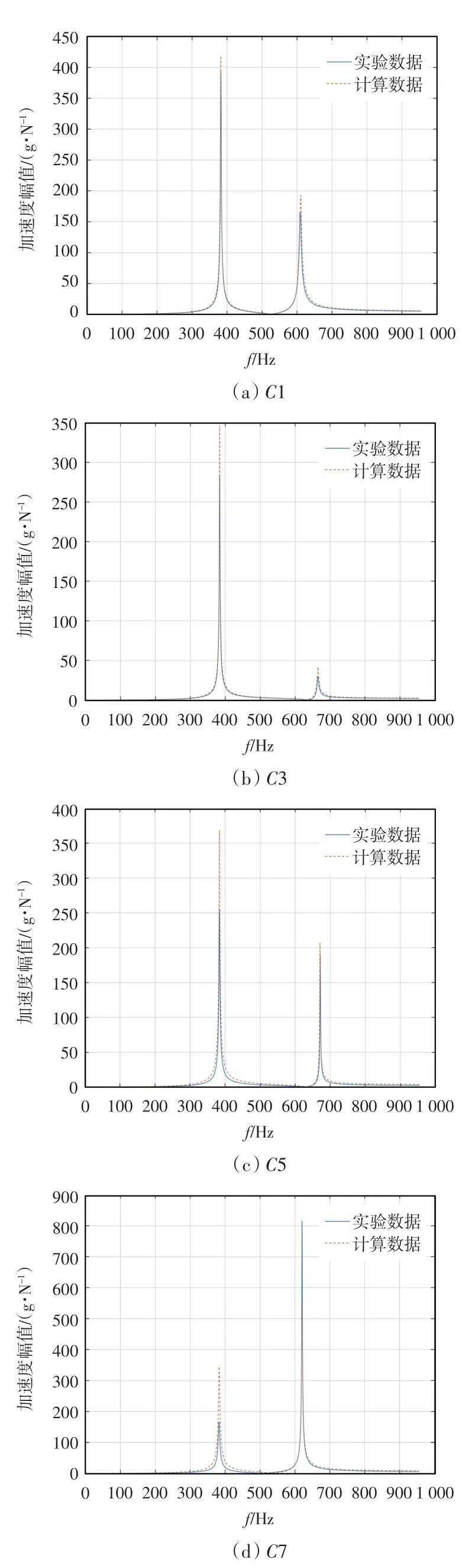
图2 平面薄壁件不同测试点的试验及仿真结果幅频图

由图2 可知，实验和拟合曲线吻合度较好。这说明提取的模态参数有效可靠。显然，仅考虑前二阶模态就可以较好地对薄壁件铣削路径上的点进行动态特性评价。

2 实验结果分析

2.1 模态参数拟合

由表1 知，与系统动态特性相关的固有频率、阻尼和留数等参数随着切削路径时变。薄壁件的一阶频率和一阶阻尼拟合结果如图3 所示，一阶留数拟合结果如图4 所示。

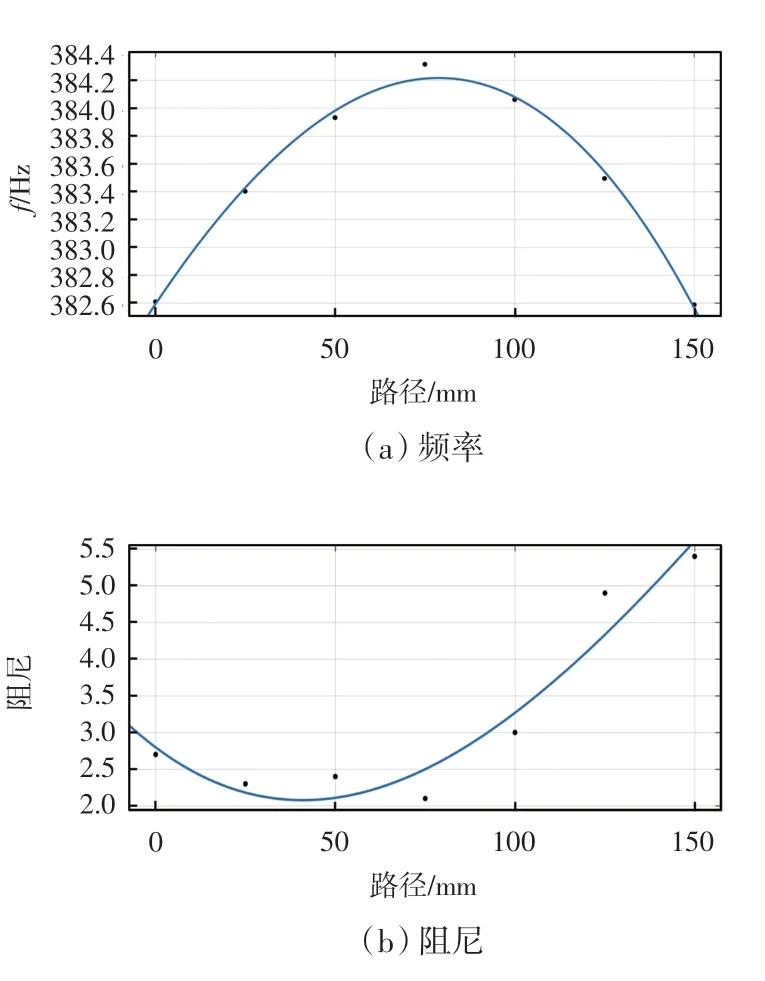
图3 平面薄壁件一阶频率、一阶阻尼拟合图

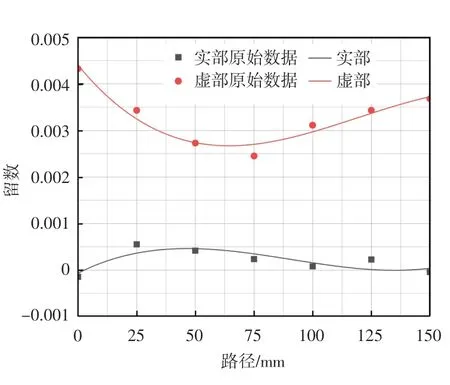
图4 平面薄壁件一阶留数拟合图

由图3（a）可知，薄壁件的一阶频率随着工件加工路径改变先增大后减小，且越靠近薄壁件中心，频率增长速率越慢；一阶频率图近似呈现为一条开口向下的抛物线，且薄壁件的中心位置频率取得最大值384.351 Hz。这是由于平面薄壁件为对称结构且薄壁件中心的刚度大于工件两侧的刚度，说明平面薄壁件中间位置固有频率更高，相较于工件两侧更不容易发生变形。

由图3（b）可知，一阶阻尼随着路径改变先减小后增大，且整体变化呈不对称趋势。

由图4 可知，一阶留数实部随着路径的改变在0 水平线上下小范围波动，最大峰谷值差为6×10-4，这说明路径变化对留数实部的影响不大，一阶留数虚部随着路径改变先减小后增大且工件中心处为最小值，整体变化近似呈现为开口向上的抛物线，在切削路径范围内切削路径的改变对一阶留数虚部具有一定程度的影响。

基于3 次多项式拟合方法，得到平面薄壁件的一阶模态参数为

一阶频率

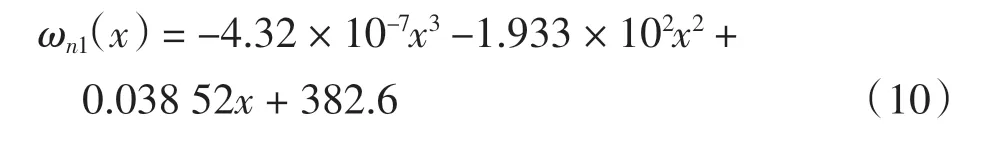
一阶阻尼

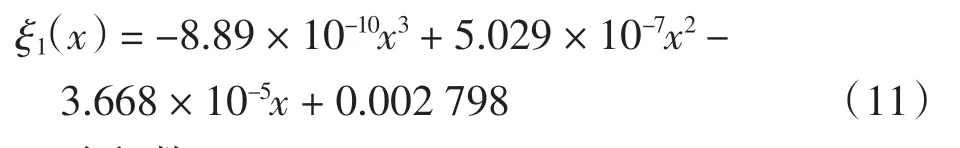
一阶留数

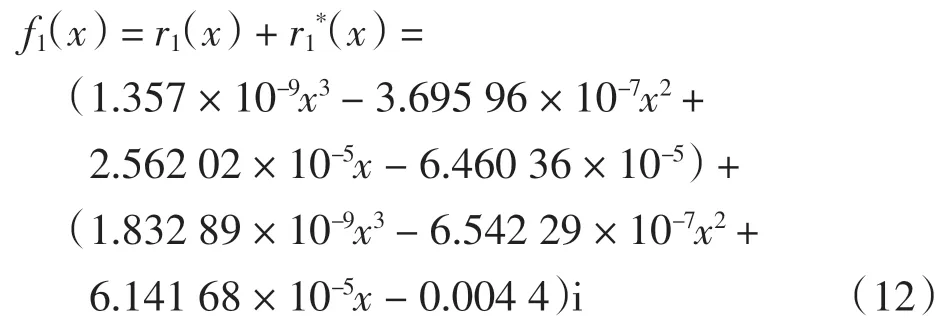
二阶频率和二阶阻尼拟合结果如图5 所示，二阶阻尼拟合结果如图6 所示。

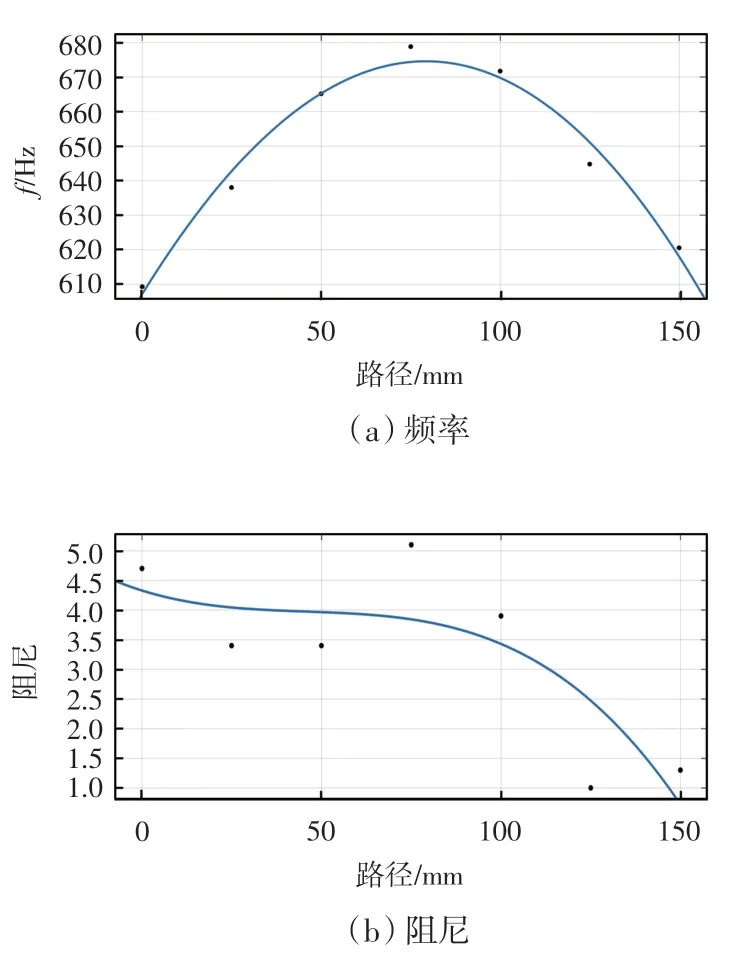
图5 平面薄壁件二阶频率、二阶阻尼拟合图

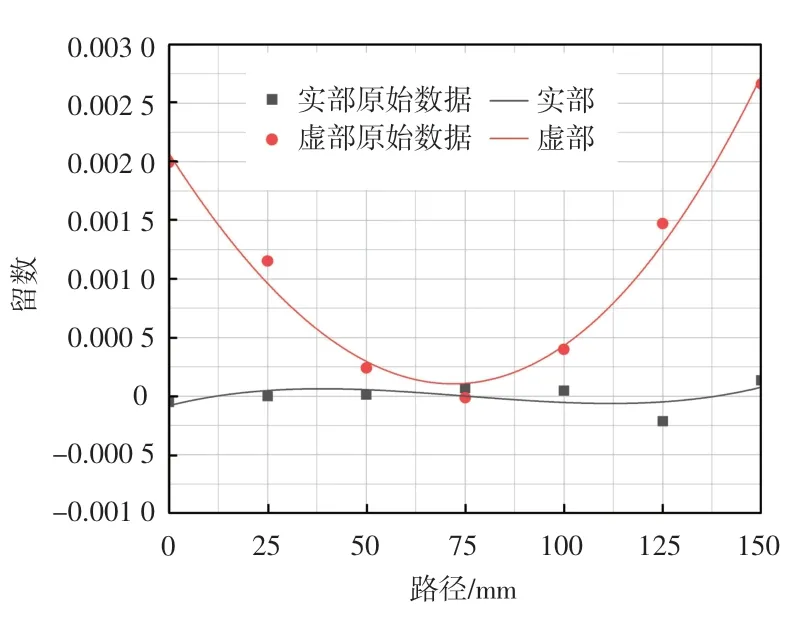
图6 平面薄壁件二阶留数拟合图

由图5（a）可知，薄壁件的二阶频率随着路径的改变先增大后减小且越靠近薄壁件中心，频率增长速率越慢，工件二阶频率曲线同样呈现一条近似于抛物线的形式，且中心位置处取得二阶频率最大值为678.787 Hz，在薄壁件的中心处刚度更大。由图5（b）可知，二阶阻尼随着路径变化一直呈现减小趋势且减小速率由慢变快，且后近似于直线降低。

由图6 可知，二阶留数实部随着路径变化在0 水平线上下小范围波动，最大峰谷值差为1.3×10-4，说明切削路径的改变对二阶留数实部影响很小，二阶留数虚部随着路径变化先减小后增大，近似呈现为开口向上的抛物线形式，工件两侧虚部数值相似且工件中心处取得最小值。这说明切削路径改变对二阶留数虚部影响程度较大。

基于3 次多项式拟合方法，得到平面薄壁件的二阶模态参数为

二阶频率

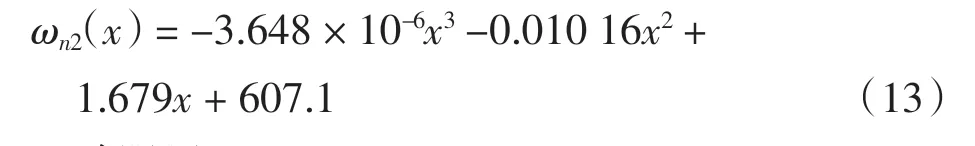
二阶阻尼

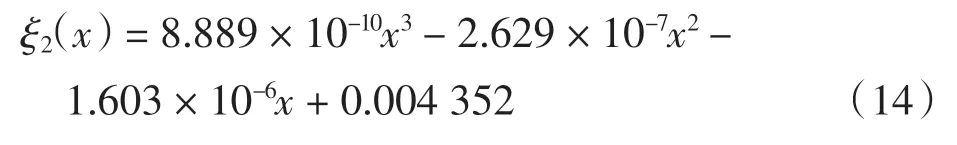
二阶留数

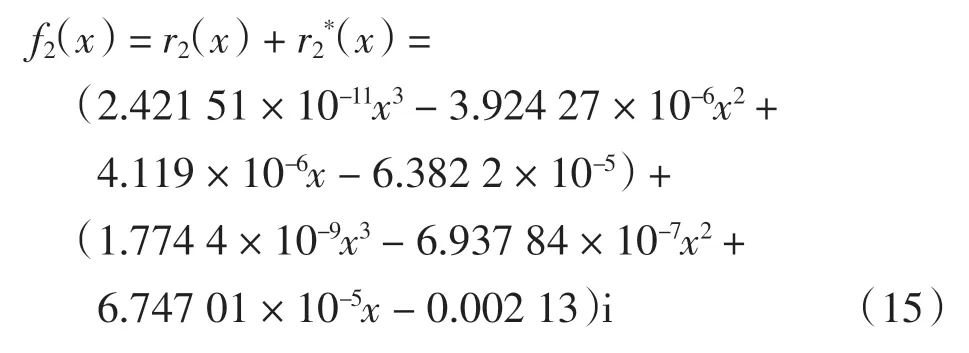
2.2 平面薄壁件动态参数预测模型

将上述平面薄壁件的模态参数，即公式（10）—（15）代入式（9）的前二阶传递函数模型中，得到平面薄壁件基于路径变化的动态特性预测模型

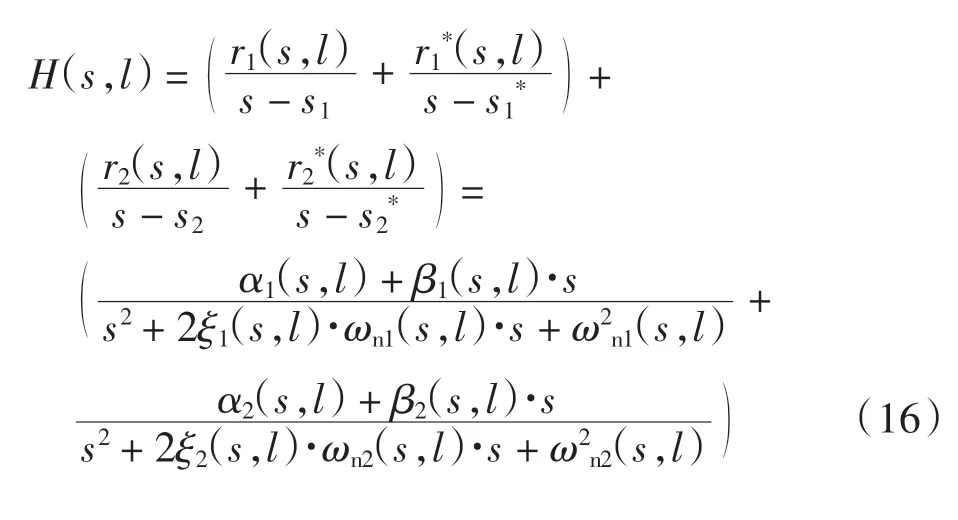
3 实验验证

为了验证上述模型的正确性，本文选取平面薄壁件切削路径上不同于测试点的任意2 点的模态参数进行理论预测并与试验结果进行对比，所选取验证点的模态参数未知。本文选取14 mm 和80 mm 两试验位置，如图1（d）中所示C8、C9 两点。

在平面薄壁件C8、C9 两点处进行锤击实验，提取前二阶模态参数，拟合得到平面薄壁件在C8、C9 点处幅频对比图，如图7 所示。

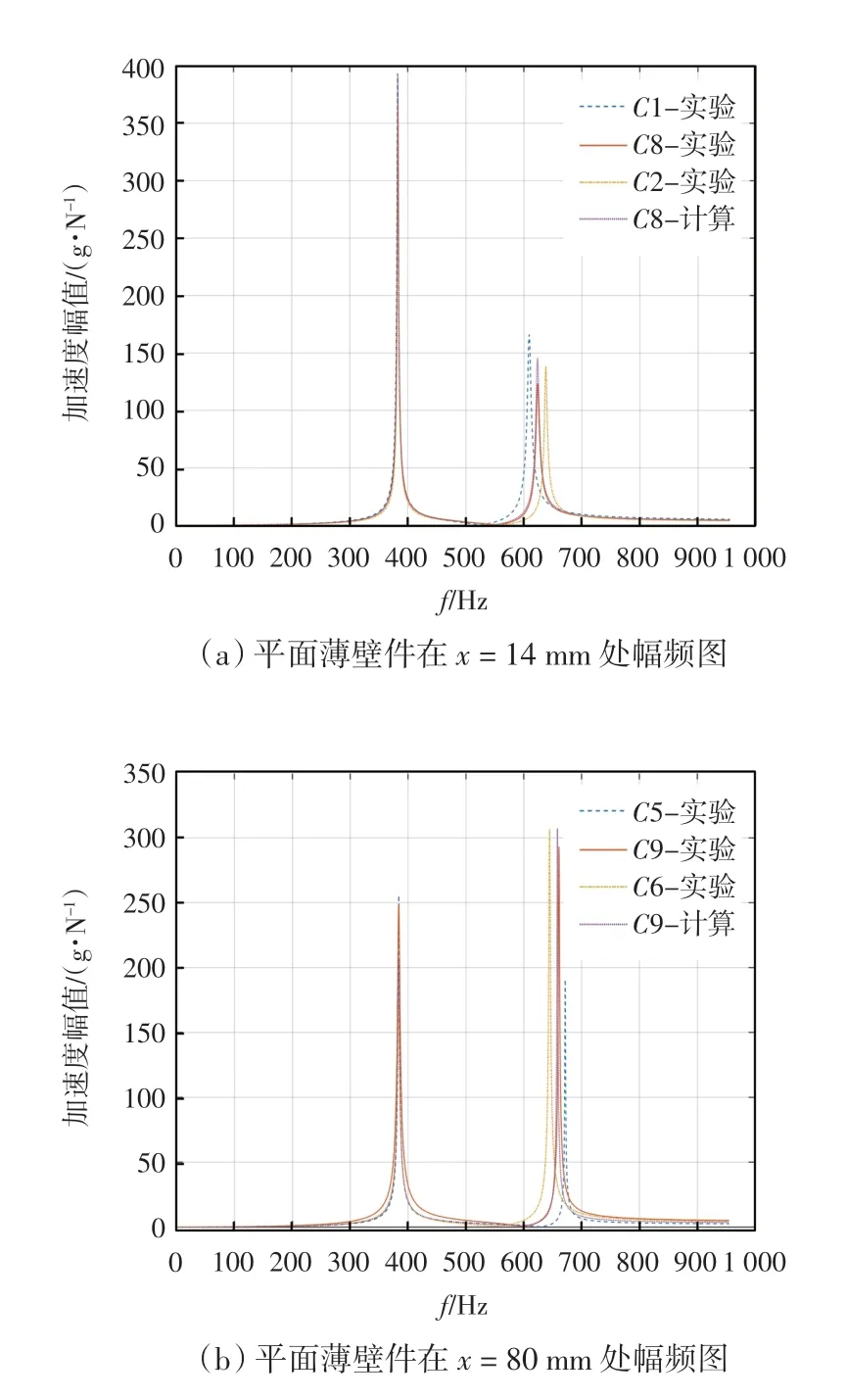
图7 平面薄壁件在C8、C9 点处幅频对比图

由图7 可知，C8 点处的预测结果和试验结果的重合度相较C9 点处的预测结果和实验结果的重合度较低。这是由于薄壁件两侧的刚度较中间位置较低，稳定性较差，所以产生的振动更大。但是，C8、C9 两点的一阶模态计算值和实验值相差不大，且二阶模态均处于相邻两测试点的二阶模态之间。这说明模型预测性较好，可较好地获得该点的振动特性。

4 结论

本文基于铣削加工过程中路径的变化，建立了平面薄壁件的动态特性预测模型，进行锤击实验并研究了铣削路径的改变对工件的模态参数的影响；建立了平面薄壁件的模态参数预测模型，对工件切削路径上任意一点进行模态参数预测。实验结果如下：

（1）切削点越靠近薄壁件中心，固有频率越高，工件变形越小。

（2）根据实验数据拟合结果发现，前二阶模态即可对切削点的动态特性进行较好的评估。

（3）随着铣削路径变化，一阶频率先增大后减小，一阶阻尼先减小后增大，一阶留数实部在0 水平线上下小范围浮动，一阶留数虚部先减小后增大且在工件中心取得最小值；二阶频率先增大后减小，二阶阻尼一直减小且减小速率先慢后快，二阶留数实部在0 水平线上下小范围浮动，二阶留数虚部先减小后增大且在工件中心取得最小值。

（4）对实验测得的模态参数进行3 次多项式拟合，构建了平面薄壁件的模态参数预测模型，该模型可对工件加工过程中铣削路径上点的模态参数进行预测。