基于形态学探针重建算法的光栅常数评定

舒瀚，王生怀，陈建瑜，邹春龙

（湖北汽车工业学院 精密测量技术研究所，湖北 十堰442002）

原子力显微镜（atomic force microscopy，AFM）根据原子之间的相互作用力对样品进行成像，凭借纳米级的分辨率和宽松的使用环境，广泛应用于多种领域［1］。在测量过程中，由于AFM探针针尖不可能无限尖锐，导致得到的表面形貌图实际为探针针尖与表面形貌卷积的结果［2］。AFM图像会因为探针的影响产生畸变［3］，而且畸变程度会随着探针半径与样品宽度的比例增大而增大，对评定光栅常数造成很大的影响。常用的AFM图像畸变消除方法如下：1）电子显微镜成像技术，比如扫描电子显微镜（scanning electron microscope，SEM）和透射电子显微镜（transmission electron microscope，TEM）等［4］；2）利用探针盲重建算法进行重建探针形貌［5］；3）研制比探针针尖更小的纳米结构的探针校准器进行探针信息提取［6］。3种方法都有各自的优缺点，使用SEM或者TEM可以对探针进行高分辨率的表征，通过获得探针尺寸来消除畸变，但只能得到探针的轮廓信息，而且测量过程会损伤探针，给评定带入新的失真；同时探针的拆卸也较为困难。探针盲重建算法通过对AFM扫描图像边缘信息提取出探针形貌信息，再通过探针形貌信息重建出探针尺寸来消除畸变。该方法不会对探针造成损伤，容易实现，然而因为没有进行标定，无法准确判断重建后的探针形貌是否为真实探针形貌，容易受到模型准确性和噪声影响［7］。通过研制探针校准器可以准确获得探针针尖圆弧半径和探针锥角信息，并且整个表征过程简单、数据易处理，但该校准器制造成本较高，研制困难。为了满足稳定并精确评定光栅常数的要求，提出一种基于数学形态学探针重建算法评定光栅常数，在Garcia模型的基础上采用数学形态学思想和标定值校正方法来提高光栅常数评定结果的稳定性和精确度。

1 AFM测量光栅常数

AFM测量仪器的原理如图1所示。在纳米尺度测量范围内，2个原子之间的作用力形式会随着距离的变化而改变，当距离较远时吸引力起主要作用，此时2个原子处于相互吸引的状态。随着两原子间距离的减小，吸引力会逐渐减弱，当该距离减小到某个值时，原子之间的作用力减小至零，随着原子之间的距离继续减小，2个原子之间的作用力将表现为排斥力。AFM利用1根对微小力极敏感的弹性微悬臂来感受探针尖端原子与样品表面原子间的作用力。系统中微悬臂的一端固定，另一端带有纳米级针尖，微悬臂受力时会发生偏折，通过检测微悬臂的偏折情况可测量出样品表面微观形貌［8］。作为纳米尺寸标准物质的一维纳米基准光栅，常用来对AFM的扫描图像进行非线性校准［9］。

图1 AFM工作原理图

2 改进的Garcia模型

Garcia模型用来表征样品尺寸大于针尖圆弧半径［10］，如图2所示，AFM扫描样品台阶时，探针圆弧在靠近样品球顶端位置参与相互作用，探针锥角在远离台阶顶部位置时与台阶发生接触。此时针尖2个锥角引起的样品台阶展宽W和针尖圆弧半径RT以及样品台阶拟合的球半径RS存在以下关系：

图2 Garcia模型

式中：α和β为探针锥角。当探针垂直接触样品时，忽略探针针尖两侧引入展宽的影响，即α与β相等。则Garcia模型改进为

AFM扫描图像除了受到探针的影响之外，也受到扫描过程中的样品上的噪声、来自外界的随机噪声、反馈控制电路中放大器和积分器等引起的噪声、由光和电的基本性质引起的噪声等影响［11］。但AFM属于纳米级测量设备，制造时考虑了环境因素的影响，所以可以把AFM扫描图像的大部分噪音看作是满足高斯分布的随机噪声［12］。高斯噪音的概率密度函数为

式中：z为图像的灰度值；μ为z的平均值；σ为z的标准差；σ2为z的方差。

3 基于形态学探针重建算法

AFM探针不是绝对的针尖结构，是随着磨损变化的复杂圆锥结构。在探针测量高低不平的样品形貌时，探针的锥角边缘部分会与样品表面形貌发生接触，导致测量结果出现误差。AFM扫描图像实际上是针尖轮廓与样品真实表面形貌卷积的结果，如图3所示。

考虑探针与样品接触没有弹塑性变形和系统响应误差的情况下，用改进Garcia模型表示扫描图像与真实表面形貌、探针形貌之间存在的关系：

式中：h为真实台阶高度；W1为真实台阶宽度；W2为扫描台阶宽度。采用数学形态学来描述改进的Garcia模型，可将探针形貌简化为

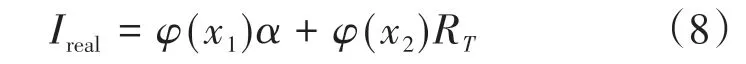
式中：Ireal为形态学结构元；RT为探针圆弧半径。则W2可用形态学的膨胀运算表示为

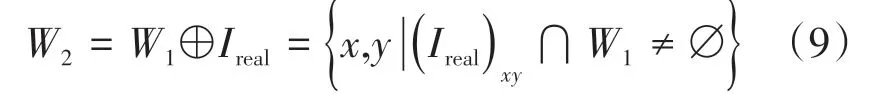
式中：x和y分别为图像像素点的坐标。

利用探针盲重建算法评定光栅常数原理如下：通过AFM得到探针形貌Iblind，将Iblind作为形态学结构元进行形态学的腐蚀运算，重建样品形貌来消除探针形貌的影响。腐蚀后图像的台阶宽度W3用腐蚀运算表示为

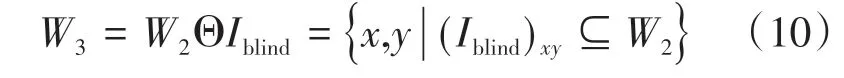
采用边缘检测算子来提取扫描图像中的光栅边缘信息，由最小二乘法构建出对应的线性函数模型来评定光栅常数值：

腐蚀后的扫描图像如图4所示。但是该算法完全依赖图像中样品和探针卷积结果来重建探针形貌，图像中高斯噪音等其他因素会对提取探针形貌造成影响，导致得到的探针形貌与真实探针形貌存在误差，最后得到W3与W1的差值也有较大误差。尤其在探针磨损严重的情况下，采用探针盲重建算法评定光栅常数的稳定性和精确度不足。

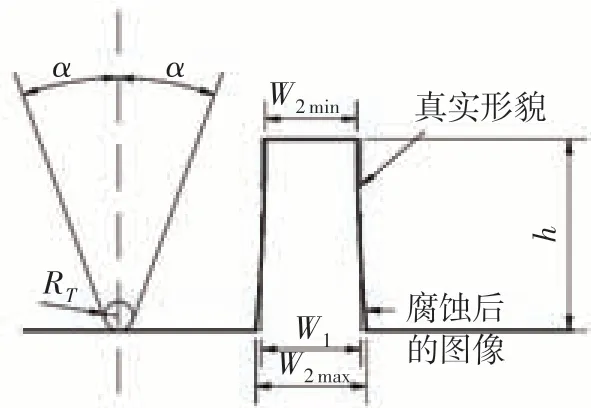
图4 腐蚀算法得到的图像

为了提高评定光栅常数的稳定性和精确度，通过控制探针形貌的特征值与真实探针形貌的特征值误差，使重建后的Irecon与Ireal相等，再由式（10）得到重建后的W3。该算法根据已知的标定值和相应的卷积结果推导出探针形貌的数学模型，通过该数学模型提高评定光栅常数的精确度。

根据W1、RT0和α0，构建出初始探针形貌I0，利用式（10）得到腐蚀后的初始台阶宽度W30。对RT和α进行遍历运算，直到ΔW满足设定的范围为止，即可保证得到的Irecon接近Ireal。利用式（10）～（11）得到相应的光栅常数值。设定第i次腐蚀得到的台阶宽度W3i与标定值W1的差值为ΔW。则其计算公式为

ΔW=W3i-W1,i=1,2,3,… （12）

为了避免该算法受到扫描图像中异常值的影响而导致结果出现畸变，在基于形态学探针重建算法中采用拉依达准则来剔除异常值。将边缘检测得到的边缘数据进行处理，计算出偏差Δd和标准偏差σ，对比最大偏差Δdmax和3σ的值，如果Δdmax大于3σ，则将其作为异常值剔除。对剩下的边缘数据进行重新计算，求出Δd和σ，直到所有Δd都小于相应的3σ为止。

4 评定方法实验结果

通过MATLAB构建一维纳米基准光栅模型，见图5。设定光栅常数d为105nm，栅距通常设为光栅常数的1/2，光栅矩阵大小为375nm×375nm。

图5 一维纳米基准光栅

探针针尖圆弧半径和探针锥角2个变量对评定光栅常数的影响结果如图6所示。探针锥角对扫描图像的光栅常数误差会随着角度的增大而增大，探针针尖圆弧半径对扫描图像的光栅常数误差始终为定值。实验以探针锥角为主要自变量，检测探针重建算法评定光栅常数的稳定性和精确度。

图6 不同参数对评定光栅常数的影响

将RT设置为10nm，采用边缘检测算子进行边缘提取并运用最小二乘法拟合得到光栅常数值。在仅受探针影响无噪音的理想状态下，探针盲重建算法与探针重建算法评定光栅常数值如图7a～b所示，随着α不断增大，2种方法评定的d值与d标定值的误差都保持在较小范围内。在有噪音的情况下，采用高斯滤波器对图像进行滤波，采用MAT⁃LAB中的randn函数对AFM扫描图像中添加均值为0，标准差为2的高斯噪音。运用基于形态学探针重建算法和探针盲重建算法评定光栅常数，如图7c～d所示，随着探针的α不断增大，探针盲重建算法得到的d值逐渐偏离光栅常数的标定值，而基于形态学探针重建算法得到的d值与d标定值误差保持在较小范围内。

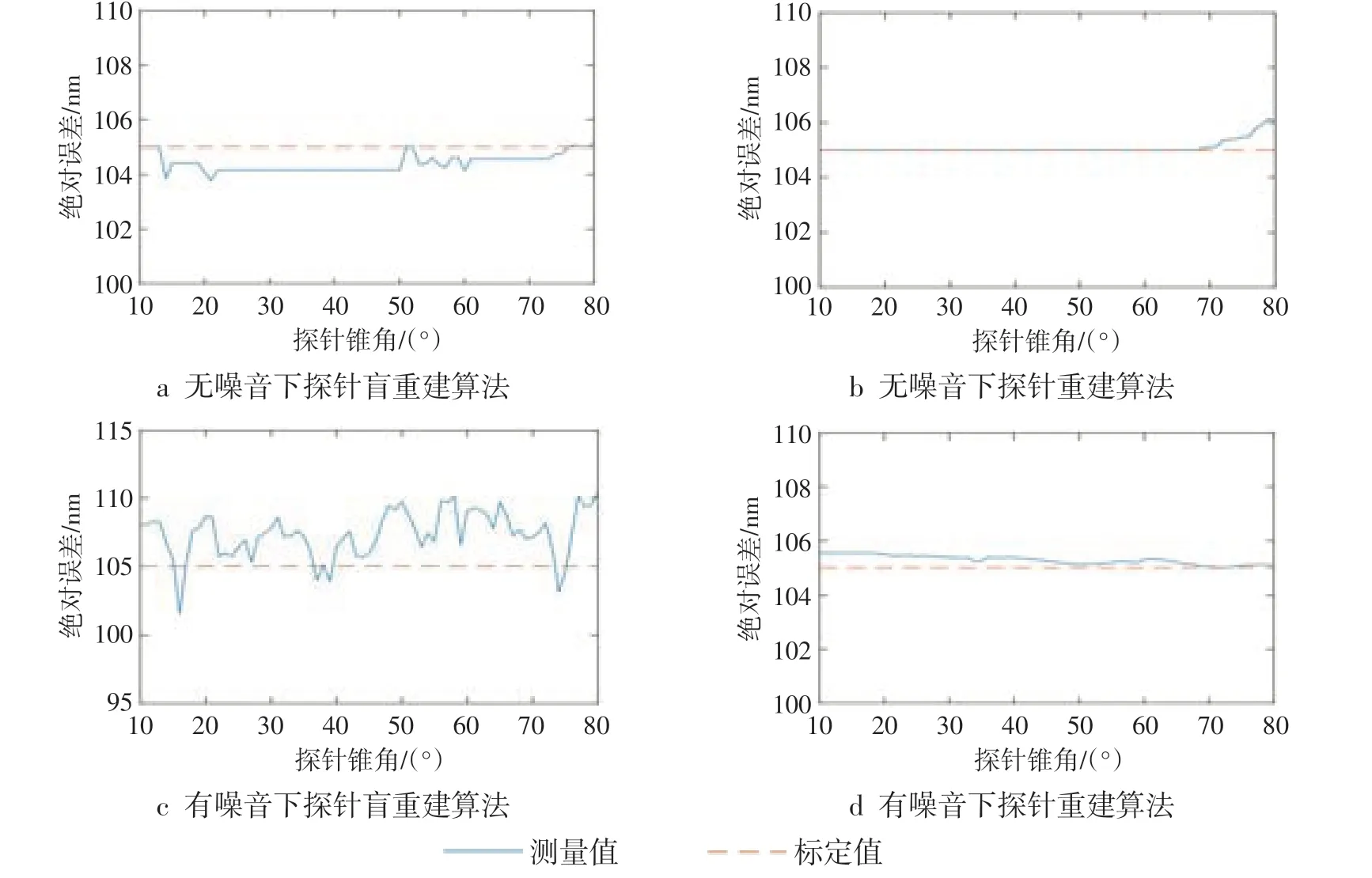
图7 不同算法评定光栅常数结果图

计算不同状态下2种算法的平均值、标准差和方差，结果对比如表1所示。探针盲重建算法得到光栅常数的平均值、标准差和方差明显大于基于形态学的探针重建算法得到的平均值、标准差和方差，而且探针盲重建算法在有噪音的情况下的标准差和方差值明显大于其无噪音的情况下的标准差和方差值，而基于形态学探针重建算法在有无噪音情况下的标准差和方差值变化较小。实验表明，基于形态学探针重建算法评定光栅常数的稳定性和精确度优于探针盲重建算法。

表1 不同状态下探针盲重建算法与探针重建算法误差对比 nm

考虑该算法在其他光栅常数下的有效性，利用该算法对标定的模拟光栅图像进行校正。采用同图2中有噪音的同等条件，校正后得到的探针形貌如式（8）所示，对其他光栅常数的一维基准光栅进行扫描，结果如图8所示，可以看出，该算法对光栅常数d的评定结果较接近于标定值。

图8 光栅常数测量值与标定值对比图

该算法在不同光栅常数下评定的平均值、标准差和方差值如表2所示。结果显示，与表1中探针盲重建算法结果相比，该算法在不同的光栅常数下仍能提高光栅常数评定的稳定性和精确度。

表2 不同光栅常数下重建算法误差对比nm

5 结论

文中在Garcia模型基础上改进、简化探针的数学模型，分析模型中的影响因素，发现探针锥角是对光栅常数测量结果影响最大的因素。在此基础上，提出基于数学形态学探针重建算法评定光栅常数。通过实验结果可知，在有无噪音的情况下和不同的探针锥角下，该算法评定光栅常数的平均值、标准差和方差值较探针盲重建算法更小，能够提高光栅常数评定的稳定性和精确度。