面向高生产率低成本的镗削切削用量多目标优化
2021-10-16杨宁李峰吴瑶胡明茂
杨宁,李峰,吴瑶,胡明茂
(湖北汽车工业学院 机械工程学院,湖北 十堰442002)
机床加工为我国经济发展做出了不少贡献,但也存在一些弊端,如加工成本高、能源消耗大、加工时间长等。要想改变这一现状,需要对加工过程中的切削参数进行优化,国内外已有大量学者进行了研究。Saravanan等[1]在机床功率和切削力等约束下,选取遗传算法和模拟退火算法优化车削参数;Hanafi等[2]为了优化车削参数,在把最小切削功率和最小表面粗糙度当作目标的基础上建立了相关模型,最后应用田口优化和灰色关联理论等方法对其进行分析;邓伟等[3]为了实现缩短铣削时间和降低能耗的目标,优化切削三要素,最后应用粒子群算法对多目标模型求解;詹欣隆等[4]以铣削加工过程中的单位体积碳排放、单位体积生产成本和工艺时间为优化目标建立模型;George P.等[5]对马氏体不锈钢进行了数控干铣削参数优化。学者们在研究过程中也使用了许多评价方法。M.S.Karthik等[6]采用田口法对数据进行分析得到最优解;马峰等[7]采用层次分析法(AHP)对产生的Pareto解集进行分析,选出满足最低加工能耗和最少切削液消耗目标的最优解集;邓朝晖等[8]采用灰色关联分析法和响应曲面法,把多个优化目标转换成单目标问题去解决,优化难度得到明显降低,最终求出合理的工艺参数;高历等[9]设计了两因素三水平实验,用于评估预测能耗模型的精确度;赵俊花等[10]应用正交试验法在复杂曲面加工中实现了能耗最低和加工时间最短的优化目标,求出了最优的加工参数和刀具路径。上述学者主要对车床铣床等进行参数优化,不涉及主要用于加工内径的镗削;在优化的分析评价部分,较少涉及模糊物元法评价方法的应用。文中以镗床为研究对象,对镗削加工进行分析,而且把能耗放到成本中的电能成本进行考虑。把高生产率、低成本定为目标,对进给量和切削速度优化,通过考虑切削力、切削功率等约束条件建立多目标优化模型,利用改进的非支配排序遗传算法对多目标模型进行优化得到Pareto最优解集,最后通过模糊物元法对最优解集分析得出多目标最优解,并把单目标和多目标结果进行比较。
1 镗削参数多目标优化模型
1.1 优化变量
切削三要素是影响镗削加工时间和总成本的主要因素,因此需要选取合理的镗削参数。切削深度可根据实际情况加以确定,一般当作确定值,故优化变量确定为进给量f和切削速度Vc。
1.2 优化目标函数

1)生产率模型 生产率由完成一道工序的时间t来表示,包括辅助时间tot、工序换刀时间tm、切削时间tc和空走刀时间tn。模型如下:式中:tot为辅助时间,在加工过程中是常量;tmt为换刀一次所需要的时间;T为刀具寿命;L为切削路径长度;d为镗削直径;tn为空走刀时间;Ln为空切路径长度;n为主轴转速。
2)加工成本模型 镗削加工过程中,成本主要有镗床折旧成本Cmt、工人成本Cla、刀具成本Cto、切削液成本Cfd和电能成本Ce,总成本模型如下:
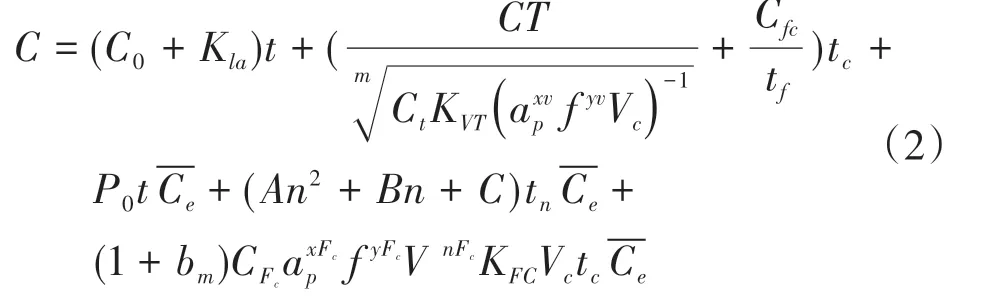
式中:C0为镗床每单位时间的折旧成本;Kla为单位时间的工人工资;CT为刀具价格;Ct为刀具寿命系数;KVT为切削速度Vc的修正系数;Cfc为一个更换周期的切削液成本;tf为切削液更换周期;P0为镗床额定功率;为电能单价;bm为比例系数;CFc为被加工零件材料以及切削条件的系数;xFc、yFc、nFC为ap、f、Vc的指数;KFC为某些因素对切削力的 修 正 系 数;为常量,可通过查表[11-12]获得。
1.3 约束条件
生产率、加工成本受很多因素约束,如切削速度Vc、进给量f、切削功率Pc、切削力Fc等。高生产率和低加工成本的参数多目标优化模型如下:
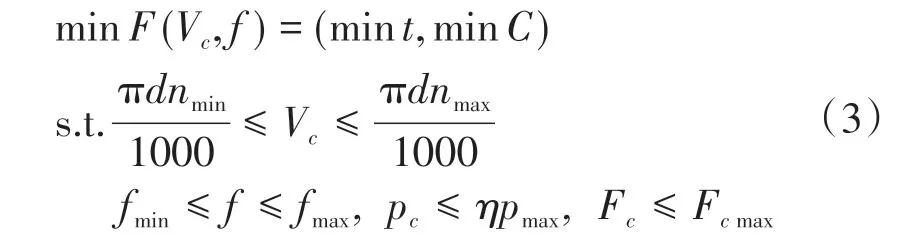
式中:nmax和nmin分别为机床允许的最大和最小转速;d为镗削直径;fmax和fmin分别为镗床加工允许的进给量最大值和最小值;η为机床加工效率;Pmax为机床额定功率;Fcmax为机床允许的最大切削力。
2 改进NSGA-Ⅱ算法
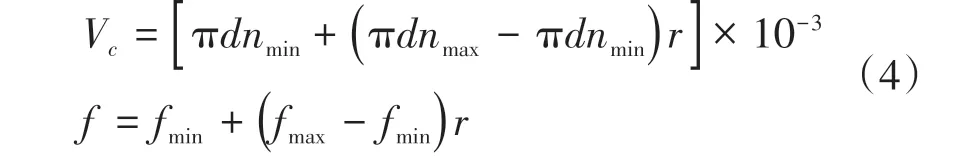
目前NSGA-Ⅱ算法应用较成功,MATLAB中的函数gamultiobj采用的是对此算法进行改进后的多目标遗传算法。算法采用的编码方法为实数编码,任意编码向量可表示为(Vc,f)。式中:r为[0,1]均匀分布的随机数。函数gamultiobj在选择运算中仅选用竞赛选择,并且基于拥挤距离和序值。函数mutationadaptfeasible和函数cross⁃overintermediate分别是函数gamultiobj默认的变异函数和交叉函数,函数ga与函数gamultiobj对应的功能相同。函数gamultiobj在运算中应用支配和排序,可以自动保留精英,不含有精英保留操作。
MATLAB中带有的函数gamultiobj的组织结构如图1所示,包含2个部分:1)确定优化问题的约束类型,由函数gacommon得以实现;2)对多目标优化问题进行求解,由函数gamultiobjsolve得以实现,先通过函数gamultiobjMakeState生成初始群体,然后判别能否退出算法,如果可以退出就生成Pareto最优解,如果不可以,先进化为新一代种群,然后作图,最后分析是否能够停止,用到的函数分别为stepgamultiobj、gadsplot、gamultiobjConvered[13]。
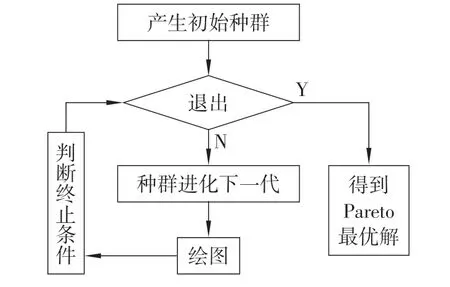
图1 多目标优化问题求解
3 案例分析
3.1 参数设置
以ZK7640型立式数控镗铣床为例,对零件进行镗削孔加工,验证上述模型和算法的合理性。机床相关参数见表1,其中P0为额定功率。待加工零件材料为碳钢,孔的尺寸为100+0.050mm。生产率计算相关参数见表2,刀具寿命相关参数见表3,成本计算相关参数见表4,其他参数设置见表5,改进NSGA-Ⅱ算法相关参数见表6。
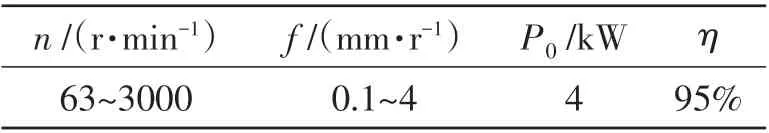
表1 镗床参数

表2 生产率计算相关参数

表3 刀具寿命相关参数

表4 成本计算相关参数
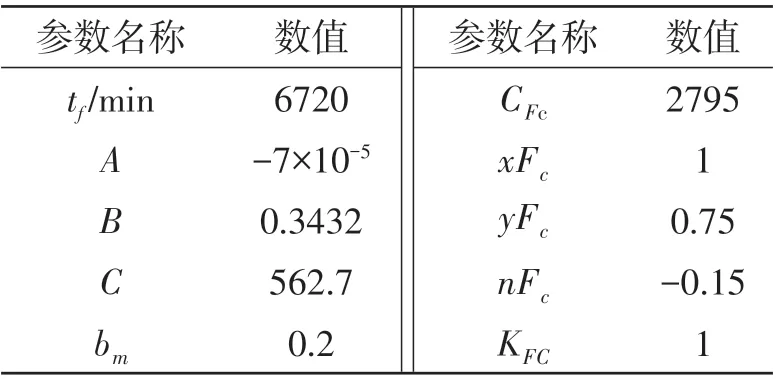
表5 其他参数设置
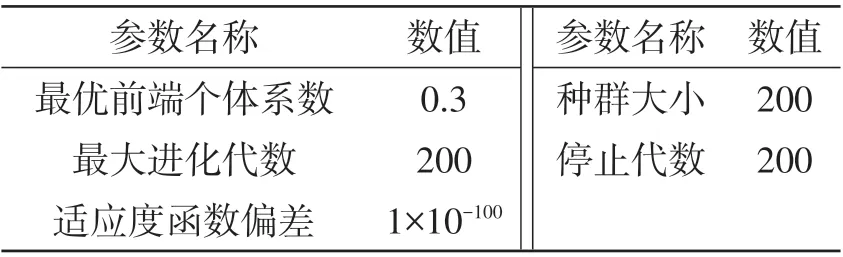
表6 改进NSGA-Ⅱ算法相关参数
MATLAB在运行过程中,改进NSGA-Ⅱ算法可以自动生成第一前端个体分布状态,并且图像会随着进化代数更新而不断变化。当优化算法停止运行后,软件会生成如图2所示的第一前端个体分布图,并且在工作区的页面可以得到60组Pareto最优解和优化目标值,如表7所示。算法每次运行后的结果都不相同,因为初始群体是任意产生的。
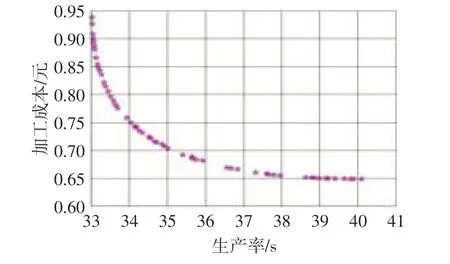
图2 第一前端个体分布图
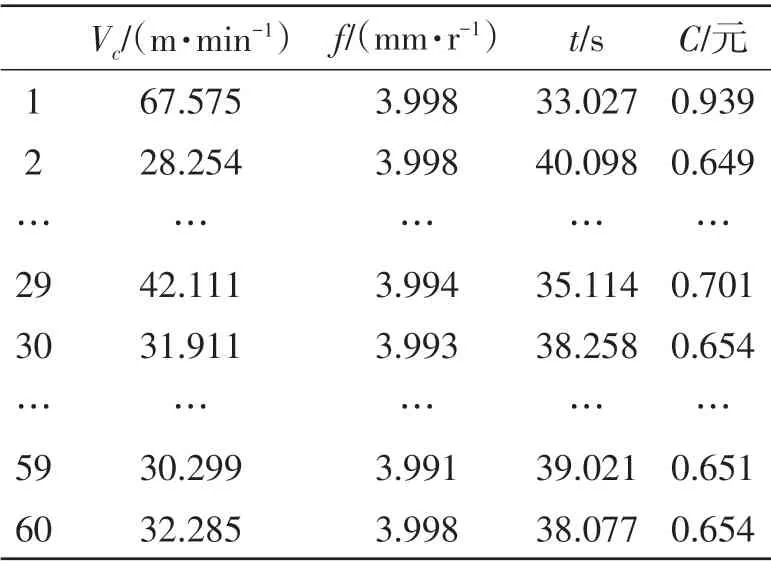
表7 某次运行得到的Pareto最优解
3.2 模糊物元分析
针对多目标决策方案,事物、特征、具有模糊特征的量值构成三元有序组,即物元,其中方案Mi为事物,评价指标Ci为特征,数值xji为量值:

在模糊物元中以隶属度来作为衡量标准,确定隶属度的方法通常有越大越优型和越小越优型。文中属于后者,对应公式如下:
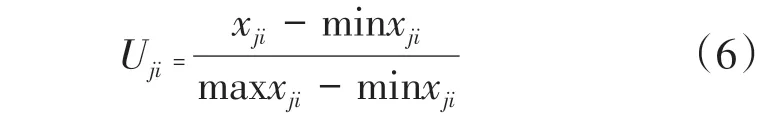
将关联系数视作等同于隶属度,所以

关联系数复合模糊物元记为

每个决策方案第i项评价指标的权重为

则每个决策方案指标的权得复合物元为Rw:
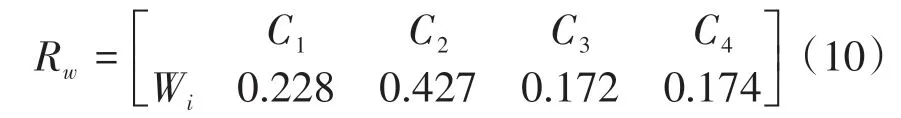
通过加权平均集中处理可以得到关联度复合模糊物元Rk:

即

对关联度进行排序,找到最小值,得出最优方案为M38,同时得到高生产率的最优方案M1和低成本的最优方案M2,对比如表8所示。由表8可知:当优化目标是高生产率时,总加工时间为33.027 s,但总成本相对较高;当优化目标是低成本时,总成本为0.649 元,但总加工时间相对较长;当优化目标是高生产率、低成本时,总加工时间为34.932 s,总成本为0.710 元,相较于低成本的40.098 s提高了12.9 %,相较于高生产率的0.939 元降低了24.4 %,结果介于2个单目标结果之间,对应切削速度为43.917 m·min-1、进给量为3.9238 mm·r-1。
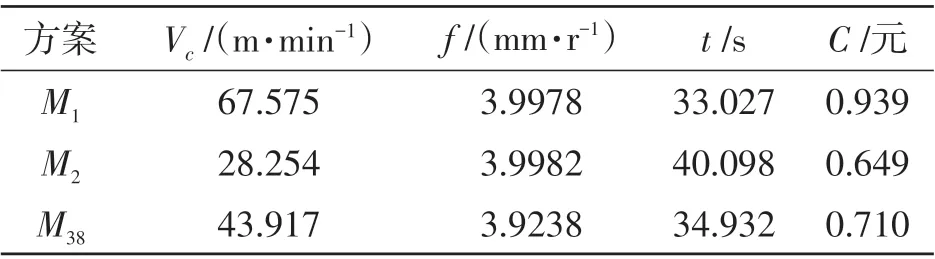
表8 最优结果对比
4 结论
以镗削速度和进给量为优化变量,把高生产率和低加工成本定为优化目标,在镗削速度、进给量、切削功率和切削力等约束条件下,建立了面向高生产率和低成本的镗削参数多目标优化模型。选取改进NSGA-Ⅱ算法优化多目标函数模型,应用模糊物元法对解集评价分析,最终得到最优的加工参数,为实现优化目标提供了合理方法。
