基于ICP算法的无人方程式赛车路径规划

邱子威，张友兵，毕栋

（湖北汽车工业学院 汽车工程师学院，湖北 十堰442002）

无人驾驶方程式大赛要求赛车具有良好的定位、感知、规划及控制能力，路径规划起关键作用。目前路径规划算法分为全局路径规划和局部路径规划。全局路径规划算法包括A*算法［1］、遗传算法［2］、蚁群算法［3］等，局部路径规划算法包括人工势场法［4］、智能水滴算法［5］、神经网络算法［6］等。迭代最近点（iterative closest point，ICP）算法应用广泛，但对2个点云初始位置要求较高，且要求2个待配准点云存在包含关系［7］。鉴于此，国内外学者提出了基于正交因子模型等改进ICP算法。路径规划方法的选择与行驶场景有关，无人方程式赛车传感器识别锥桶为坐标点集，传统ICP算法对点集坐标路径规划略有不足，通过狭窄通道时无法找到可行路径易陷入局部极小点。改进ICP算法不必对处理的点集进行分割和特征提取，收敛性较好，且计算量小很多。文中基于ICP提出适合无人方程式赛车的路径规划算法，根据已知赛道信息和当前信息规划出赛车可行驶的全局路径。

1 赛道分析

以8字环绕项目为例，提出路径规划方法。赛道由2个同心圆成8字形排列，圆心之间距离为18.25 m，内圆直径为15.25 m，外圆直径为21.25 m。在内圈内侧和外圈外侧布置16个交通锥标，两圆切点处使用高锥桶作为切点处的标识，赛道内外圈之间是3m的赛道，赛车出入于两圆相切的3m宽赛道，如图1所示。ICP算法即给定有部分重叠的参考点集和当前点集，根据2组点集中点的对应关系，求点集之间的变换关系［8］，如图2所示。8字环绕赛道点云数据重叠率较高，采用ICP算法可快速计算出可行驶轨迹，系统复杂度低。

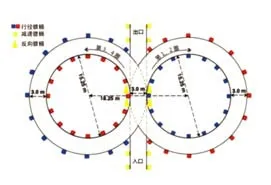
图1 赛道示意图

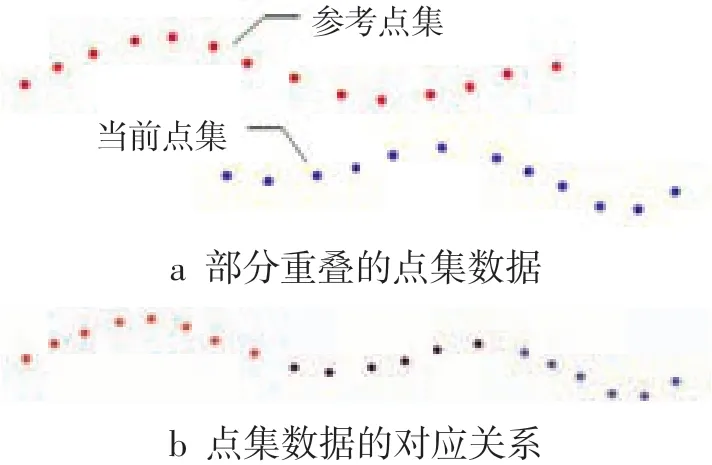
图2 信息点集数据

2 点集变换参数求解

在同一坐标系下，将某个当前点集B变换到参考点集A，假设需要点集在x方向平移Δx，y方向平移Δy，点集整体旋转Δφ。旋转矩阵R为

平移向量T为

则参考点集A与当前点集B变换关系为

算法流程如图3所示。

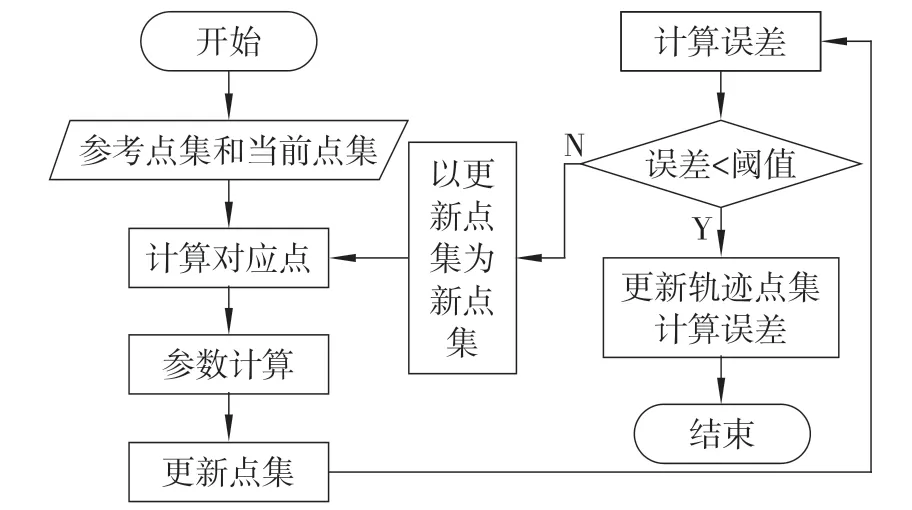
图3 ICP算法流程图

给定A和B，以8字环绕左侧入口第1个坐标点为原点，寻找公共重合部分点集{ai}和{bi}，进行中心位置配准，求出{ai}和{bi}的中心点Ca和Cb：

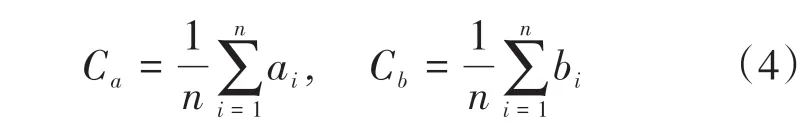
设置对应点距离和函数为

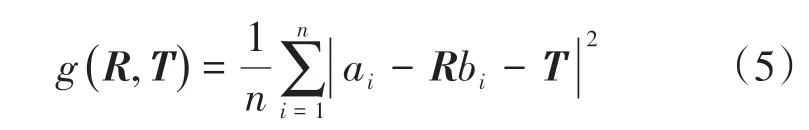
新目标函数为

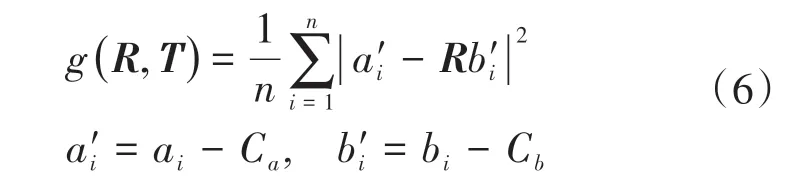
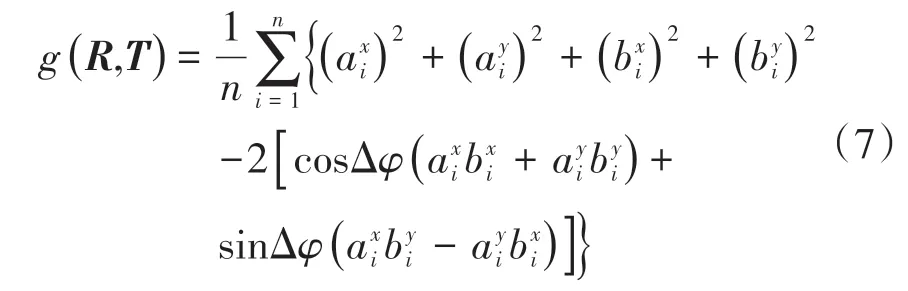
可以看出式（6）中已经将平移向量T滤除，需要求解的未知量只有R。将式（1）代入式（6）得：式中：、分别为a'i在x、y方向的分量；分别为的x、y的分量；'、分别为{ai}、{bi}（i=1，2，…，n）中每个点到点集中心的差值；Δφ为2组点集间的旋转角度。、、和为定值，不会随R的变化而改变，要使目标函数g（R,T）的值最小，只要让式（8）取最大即可。

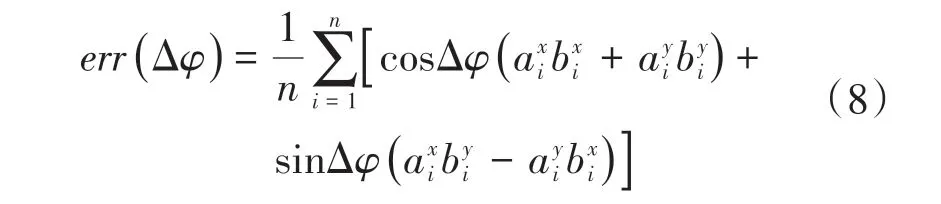
两边对Δφ求导可得：

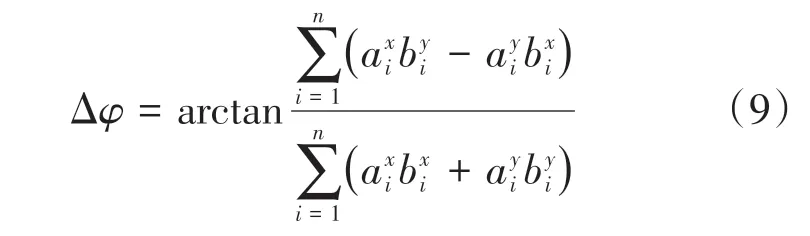
通过Δφ可求得R，{ai}和{bi}的T由式（10）求得：

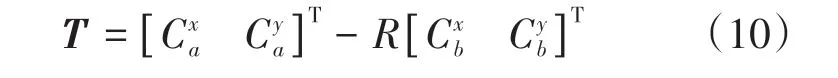
将最新变换出的矩阵C与目标点云进行计算，损失函数为对应点距离平均和：

当迭代得到的损失值大于设定的最小阈值即L大于Lmin时，则以更新的点集C为新点集，重复进行迭代计算。反之将R和T代入轨迹点集：

式中：P'为更新后的轨迹点集；Q为标准正确轨迹点集；σ为轨迹均方根误差。

3 仿真验证

以赛道入口2个高锥桶中点为原点，得到8字环绕全部锥桶坐标点集，将该点集作为参考点集。无人方程式赛车传感器有效识别最远为20m，有效识别最大角度为92°，根据原点坐标得到当前可识别锥桶。参考轨迹点集选取8字环绕项目赛道中间位置，如图4所示。

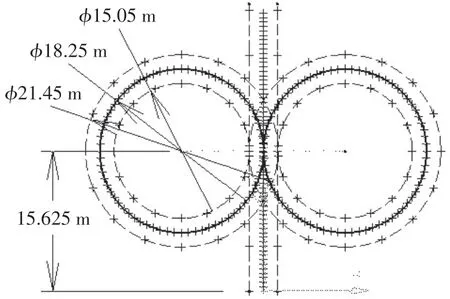
图4 赛道参考点集

将参考点集、参考轨迹点集和当前点集导入MATLAB仿真环境中，根据所有坐标点集与左侧入口第1个坐标点距离得到参考点集与当前点集重合部分，将重合部分进行ICP迭代计算得到旋转矩阵和平移向量，最后将其代入参考轨迹点集，输出当前轨迹点集结束计算。图5为模拟的8字环绕赛道，当前点集与目标点集有一定的角度和位移偏差，该赛道能较好地验证算法的有效性。由图6可知，该算法能较好地规划出行驶路径，保证赛车行驶路径基本处于赛道中间位置，3次测试的轨迹均方根误差分别为0.1251 m、0.1423 m、0.1361 m，平均值为0.1345 m，误差较小，而且路径连续光滑，符合汽车运动学规律。

图5 赛道模拟

图6 路径规划效果图

4 结论

以8字环绕赛道为例，提出了适合无人方程式赛车的路径规划方法。在赛道信息已知条件下，该方法可规划出连续光滑，基本处于赛道中间的可行驶轨迹，使赛车可以安全可靠地通过赛道，该方法可拓展应用到直线加速项目中。在较好的初值情况下，可得到较好的算法收敛性，但实际应用中可能会出现较小的角度偏差，导致在远端位置赛车碰到锥桶，后续将继续研究。