极限工况下主动前轮转向滑模控制对比

江子旺，冯樱，乔宝山

（湖北汽车工业学院 汽车工程学院，湖北 十堰 442002）

在高速、低附着路面的极限工况下，车辆的横向稳定性对车辆的行驶安全性有着重要影响。前轮转角是车辆横向动力学稳定性的影响因素之一。当出现危险工况时，主动前轮转向（active front steering，AFS）机构在不干预驾驶员转向输入的情况下，给前轮很小的附加转角，从而获得理想的转向特性，改善车辆的操纵稳定性。相比电子稳定控制系统（ESP），AFS的优势在于不采用制动或者驱动的情况下对车辆的稳定性进行控制，对纵向速度影响较小，能保证车辆的乘坐舒适性［1］。主动转向控制因其特有的优势，国内外学者进行了相关的研究。刘奋等人［2］采用定量反馈的方式制定主动前轮转向策略，将整车系统视为有界、不确定系统，其动态特性受反馈控制系统控制,以跟踪车辆期望横摆角速度。余卓平等人［3］基于相平面法分析了车速、路面附着条件及前轮转角对车辆横向稳定域的影响,提出了AFS系统的控制目标及结构,基于横摆角速度设计了H∞反馈和前馈控制器，并进行综合控制。由于滑模控制系统的行为与外部可控方向的干扰无关，适应性较高，回应比较快，对参数变化不敏感、鲁棒性好。D.V.Thang Truong等人［4］提出了采用积分滑模面的自适应滑模控制理论的鲁棒控制策略，相比传统的滑模控制方法，保证了系统在出现侧向风、低附着系数等扰动和不确定性因素时的可驾驶性和稳定性。周兵等人［5］在设计主动转向控制策略时充分考虑了路面附着对车辆横摆响应的影响，并对路面附着系数进行修正。夏长高等人［6］在设计主动前轮转向滑模控制策略时利用RBF神经网络来实时地调节滑模切换增益，以抑制传统滑模控制带来的“抖动”问题。李绍松等人［7］考虑到Pacejka等非线性轮胎模型有助于扩展车辆稳定范围，提出一种改进型线性时变模型预测控制（LTV-MPC）策略，提高了主动前轮转向汽车极限工况下的稳定性。除了理论及控制算法的研究，国外一些车企已经将主动转向技术应用到一些高端车型上。如宝马公司与采埃孚（ZF）公司联合开发的主动转向系统，通过行星齿轮机构将电机转角附加到前轮转角输入上，并成功应用于宝马5系和7系。以上学者在设计控制器时仅考虑对车辆横摆角速度的控制，忽略了质心侧偏角。当质心侧偏角较小时，横摆角速度能够表述车辆的运动状态；当车辆发生侧滑、甩尾等情况时，质心侧偏角会很大，此时横摆角速度不能正确反映车辆状态，因此需要对质心侧偏角进行控制。文中综合考虑2项指标设计了3种主动前轮转向滑模控制器，并采用指数趋近方式对趋近轨迹进行限制。基于动力学仿真软件TruckSim和Simulink搭建联合仿真模型，在低附着条件路面上采用双移线工况对3种控制器的合理性进行验证。

1 汽车动力学模型

线性二自由度车辆模型是研究车辆稳定性的重要动力学模型，忽略了转向系统和悬架的影响，认为车辆纵向速度为定值，只有侧向和横摆2个自由度，如图1所示，其中αf、αr为前后轮侧偏角，FYf、FYr为地面对前后轮侧向反作用力。

图1 二自由度车辆模型

在侧向加速度小于0.4 g时，线性二自由车辆模型能较好地反映车辆稳态响应，用于计算车辆的横摆角速度和质心侧偏角，微分方程为［8］

式中：β为质心侧偏角；k1和k2分别为前后轴总的侧偏刚度；m为整车质量；u为车辆纵向速度；ωr为横摆角速度；a和b分别为质心至前轴、后轴的距离；δ为前轮转角̇为质心侧偏角变化率为横摆角速度变化率。

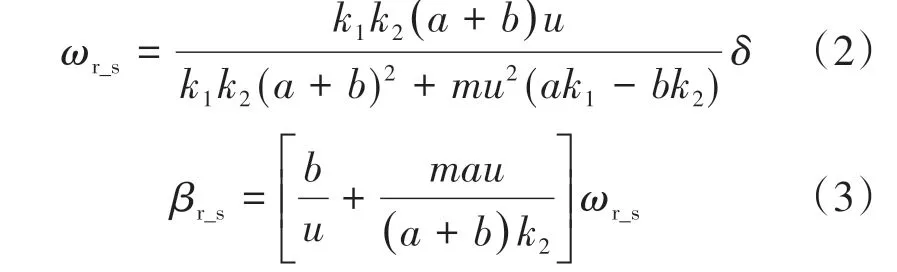
当质心侧偏角较大时，驾乘人员容易产生恐慌，因此假设车辆的质心侧偏角及其变化率都很小。同时考虑到车辆侧向加速度受轮胎-地面间附着极限的约束，最大横摆角速度ωup和最大质心侧偏角βup分别为［9］

综合式（1）～（5），得到稳定工况下期望横摆角速度ωd和期望质心侧偏角βd为［10］

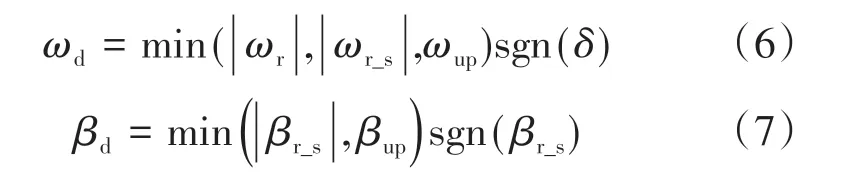
2 控制器系统设计

AFS系统控制如图2所示，二自由度参考模型和TruckSim整车模型在前轮转角输入下，分别得到期望的质心侧偏角βd和横摆角速度ωd以及实际的质心侧偏角β和横摆角速度ωr。将ωr和ωd的误差、β和βd的误差作为滑模控制器的输入，控制器输出为附加前轮转角Δδ，输入TruckSim整车模型。

2.1 滑模控制率

滑模控制的目标是通过设计合适的滑模面使系统沿规定轨迹作“滑模”运动。传统滑模控制只满足趋近条件和滑模条件，保证滑动模态状态在有限时间内趋于滑模面，并沿着滑模面运动，没有对趋近运动的轨迹进行限制。文中采用基于指速趋近律的方法设计滑模控制器，从而改善趋近运动的动态品质，表达式为［11］

十九大报告提出要大力实施乡村振兴战略，科学制定规划，健全城乡融合发展体制机制。发展“互联网+农业”，多渠道增加农民收入，促进农村一二三产业融合发展，成为实现乡村振兴的重要途径。电子商务作为一种有异于传统销售的模式，可以扩大农产品的销售渠道。自我国互联网技术的出现以来，借助网络来进行农产品销售也较为普遍。在农产品的发展中，水果类产品电子商务发展速度居于前列。烟台福山区的大樱桃作为烟台市第二大水果产业，发展大樱桃的电子商务最有重大的意义。笔者希望通过对福山大樱桃电子商务的发展进行分析，给出建设性意见。

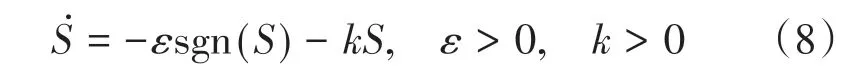
式中：k和ε为控制器参数。为了保证滑动模态状态快速趋近滑模面的同时减小抖动，在增大k的同时减小ε。指数趋近律中，指数趋近项-kS使系统在趋近滑模面的同时速度逐渐减小，而等速趋近项-εsgn(S)使系统到达滑模面附近时的趋近速度是ε而不是0。较小的速度有效防止系统产生剧烈抖动，同时保证了系统能在有限时间内到达滑模面。

2.2 滑模面设计

主动前轮转向滑模控制器选择车辆横摆角速实际值与期望值之间的误差e1、质心侧偏角实际值与期望值之间的误差e2作为控制误差输入给滑模控制器。文中分别基于e1、e2以及综合考虑e1和e2设计3种滑模控制策略，用于主动前轮转向控制，e1、e2如式（9）～（10）所示。

2.2.1 基于横摆角速度的滑模控制

控制器1是基于横摆角速度的滑模控制，以e1作为控制误差，切换函数设计为

式（11）中对e1的积分项主要是为了限制稳态误差。对式（11）求导得：

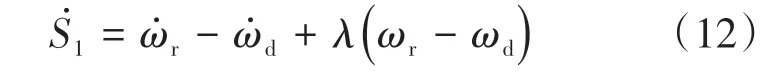
由切换函数和趋近律函数可得：

因此系统是渐进稳定的。联立式（1）、式（8）和式（11）～（12）得到前轮转角控制率δ'1：

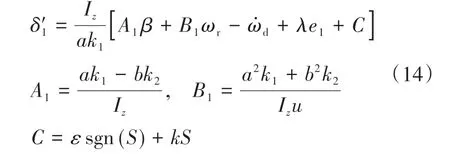
控制器2是基于质心侧偏角的滑模控制，以e2作为控制误差，切换函数设计为

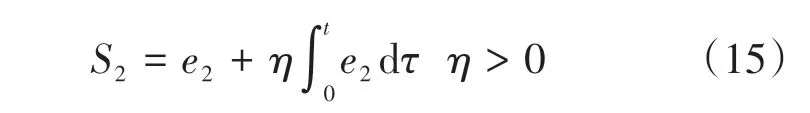
同理可得S2Ṡ2＜0，因此系统是渐进稳定的。对切换函数进行求导，并联立式（1）和式（8）得到前轮转角控制率δ'2为

2.2.3 基于质心侧偏角和横摆角速度的滑模控制

控制器3是基于质心侧偏角和横摆角速度的滑模控制，以e1和e2作为控制误差，设计滑模切换函数，一般为

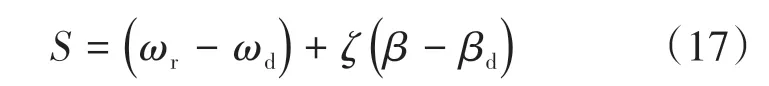
一些学者采用式（17）作为滑模切换函数［12-13］，但存在一些问题。在某些情况下不能保证e1和e2同时收敛到零。若e1和e2符号相同，当轨迹到达S=0时，e1和e2肯定会消除。然而随着驾驶条件的变化e1和e2的符号会发生改变，当e1=-e2时，S=0可能也成立，产生虚假达到的现象，实际上滑模控制器已经失效。其次，e1和e2量纲不同，此处ζ是一个有量纲的量，不代表权重。

综上所述，采用Chunyun Fu等人［14］提出的滑模切换函数：

为了解决抖振的问题，用饱和函数sat（）代替δ'1，δ'2，δ'3中的符号函数sgn（），饱和函数为

式中：ξ为边界层厚度。控制稳定性随边界厚度的减小而增加，但是控制增益会相应增大，即( )

-ξ,ξ间函数斜率增大，抖动也会相应增大；当ξ增大，控制增益和抖动会减小，但是控制稳定性会变差。

3 仿真验证与分析

为验证3种控制器在极限工况下的可行性和有效性，基于TruckSim和MATLAB/Simulink搭建联合仿真模型，路面附着系数取0.3，在不同车速下进行双移线工况试验。在TruckSim中选择两轴厢式货车作为仿真车辆，相关参数如表1所示。

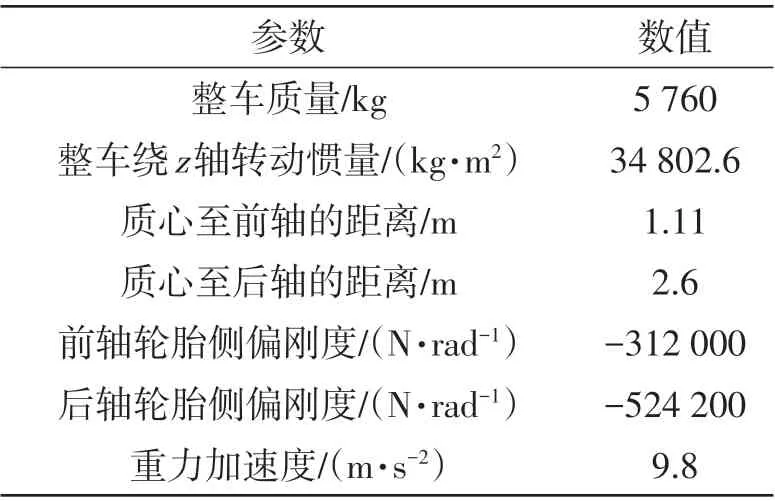
表1 整车参数

取车速为54km·h⁻¹，在双移线工况下进行仿真，得到不同控制策略下的横摆角速度和质心侧偏角响应情况，如图3所示。横摆角速度响应反映了车辆操纵稳定性。由图3a可见期望横摆角速度随驾驶员前轮转角输入增加而增加。控制器1作用下车辆能快速跟踪期望横摆角速度，有效提高车辆操纵稳定性，而控制器2和控制器3作用下的车辆无法跟踪期望横摆角速度。质心侧偏角响应是描述车辆行驶过程中对轨迹的跟踪能力。从图3b可看出，车辆在控制器2和控制器3作用下能快速、有效跟踪期望质心侧偏角，轨迹跟踪能力好，而控制器1无法实现有效跟踪期望值。

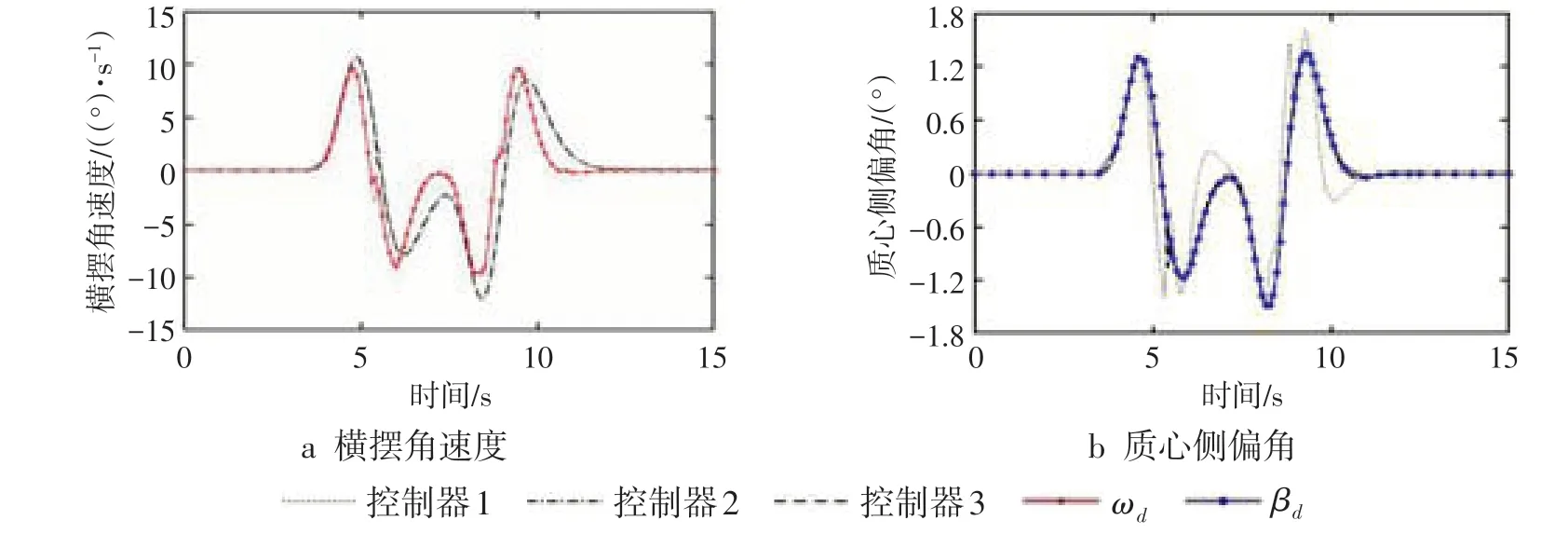
图3 车速为54km·h⁻¹时横摆角速度和质心侧偏角的仿真结果

车速为90km·h⁻¹时的横摆角速度和质心侧偏角曲线如图4所示。从图4a可知，由于控制器1和控制器3的作用，车辆横摆角速度快速、稳定地趋于期望值，提高了车辆的操纵稳定性；而控制器2作用的车辆无法跟踪不断变化的期望值。从图4b可知，控制器2作用的车辆对期望质心侧偏角的跟踪性能最好，一定程度上改善了车辆轨迹跟踪能力，但这是以牺牲期望横摆角速度的跟踪性能为代价的；而其他控制下的车辆无法跟踪期望质心侧偏角，轨迹跟踪性能较差。进一步分析图4b可知，车辆在3.4 s和5.3 s时质心侧偏角跟踪性能突然变差。车速为90km·h⁻¹时，控制器2作用下前轴轮胎侧向力曲线见图5，车辆在3.4 s和5.3 s时前轴轮胎侧向力在峰值处突然下降，说明此时前轴已经发生侧滑。车辆轮胎具有非线性特性，当轮胎特性处于线性区时，转向轮转向性能好，车辆能够根据驾驶员意图进行转向行驶。车辆横摆角速度增益可以表述车辆的转向能力。车速为90km·h⁻¹时，车辆前轮转角与横摆角速度增益的关系如图6所示：横摆角速度增益开始随着前轮转角的增加大约呈线性增加，此时转向性能好；达到最大值后迅速减小，此时轮胎已进入饱和区，转向性能迅速变差。

图4 车速为90km·h⁻¹时横摆角速度和质心侧偏角的仿真结果

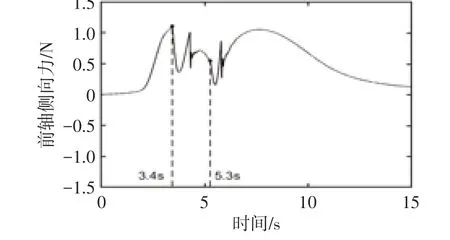
图5 车速为90km·h⁻¹时控制器2前轴轮胎侧向力

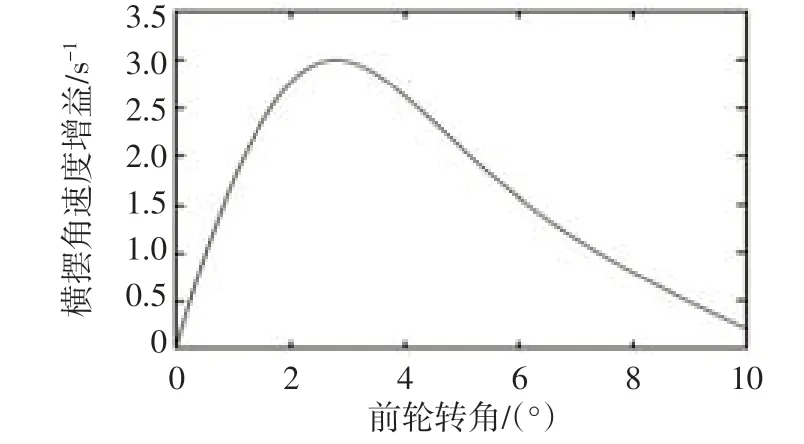
图6 前轮转角与横摆角速度增益关系

4 结论

文中建立了TruckSim整车动力学模型和二自由度参考模型，基于横摆角速度和质心侧偏角设计了3种主动前轮转向滑模控制器；搭建了TruckSim/Simulink联合仿真模型，在双移线工况下对控制策略进行验证，结果表明：1）在低附着系数路面上，基于横摆角速度的滑模控制器在中、高速下均能有效实现车辆实际横摆角速度对期望值的跟踪，但轨迹跟踪能力较差；基于质心侧偏角的滑模控制器仅在低速下使得车辆质心侧偏角有效趋于期望值，在中、高速下则无法快速稳定地实现对期望值的跟踪。基于横摆角速度和质心侧偏角综合考虑的滑模控制器在中等车速下可跟随期望质心侧偏角，而在高速下可以跟随期望横摆角速度。横摆角速度获取方便、直接，而质心侧偏角只能估算，获取成本高且不准确，因此主动前轮转向滑模控制策略的制定建议采用基于横摆角速度的方法。2）基于横摆角速度的滑模控制器在不同车速下均能快速、稳定跟踪期望横摆角速度，同时能在一定程度上减小车辆质心侧偏角，但与期望值仍存在偏差。建议在轮胎处于线性区域时采用主动前轮转向，而在轮胎非线性区仍与其他控制技术如直接横摆力矩控制的协调作用来实现二者实际值对期望值的有效跟踪，提高车辆操纵稳定性的同时改善轨迹跟踪性能。