汽车横向稳定杆支座连接结构疲劳分析
2021-10-16吴道俊蔡鸿毅张今敏郭宏瑜高扬
吴道俊,蔡鸿毅,张今敏,郭宏瑜,高扬
(厦门金龙联合汽车工业有限公司,福建 厦门361023)
客车悬架稳定杆支座的底架连接结构是车身骨架的集中载荷输入点,承担着较大的动态载荷,由于底架为方钢焊接结构,抗疲劳强度较弱[1],因此,研究该区域的疲劳问题及分析方法,具有重要意义。潘金坤[2]采用有限元方法,参照行业标准直接确定等幅正弦载荷加载,对稳定杆进行疲劳计算。王国丽[3]等研究稳定杆连杆支架,载荷通过直接测试获取,需要购买价格较贵的传感器,安装较困难。徐国权[4]采用有限元建模,施加±50mm的强制位移载荷,运用疲劳性能曲线计算稳定杆支座的疲劳寿命。上述都是参照行业标准工况,通过有限元方法对稳定杆及支座加载等幅正弦载荷,直接进行疲劳计算。对于通过稳定杆应变测试与CAE相结合获取稳定杆吊杆的随机载荷谱的研究较少,考虑稳定杆吊杆的焊接连接结构的疲劳分析的研究也较少。文中将CAE与实车试验测试相结合,研究疲劳分析方法和技术方案,对稳定杆支座底架连接结构(焊接结构)的设计结果进行疲劳计算。
1 CAE与测试相结合的方法
利用有限元分析,建立稳定杆几何中心处应变与端部的位移的关系。基于实测应变载荷谱,计算获取端部动态位移,作为稳定杆多体动力学模型输入,获取稳定杆吊杆对支座的动态载荷谱,结合焊接结构SN曲线,实现稳定杆支座的底架连接结构全局疲劳计算。具体技术路线如图1所示。
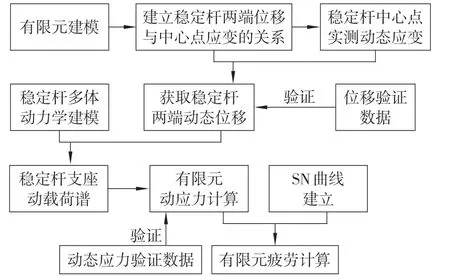
图1 稳定杆支座连接结构疲劳分析技术路线
2 稳定杆两端动位移获取及验证
由于位移信号难以测试,因此采用间接法获取。在HyperWorks中对稳定杆有限元模型(图2)两端分别按表1加载Z向位移,衬套连接处约束6个自由度,读取稳定杆前表面中心点(中间横截面表面的点,简称稳定杆中心点)与轴线成45°的应变(简称中心点应变)数据,如表1所示。稳定杆两端Z向位移与稳定杆中心点应变呈现线性关系,通过表1计算应变与左端Z向位移的比值,并取平均值获取综合比例系数为54.2。

图2 横向稳定杆有限元模型

表1 稳定杆两端Z向位移与中心点应变的关系
强化工况试验载荷谱采集获取的稳定杆中心点(与表1应变读取点和方向一致)的应变谱,如图3所示。利用表1的比例系数,计算得到左端点动位移如图4所示,右端点的位移相位正好相反。

图3 稳定杆中心点实测应变谱

图4 稳定杆左端点动态位移谱
为了确定基于有限元计算的稳定杆端部Z向位移的有效性,通过测试获取验证数据。由于位移传感器难以安装,在稳定杆端部和正上方车身底架布置垂向加速度传感器,以测试加速度计算获取动态Z向位移信号。按照文献[5]中的方法,将加速度信号转化成位移信号。由于加速度传感器在1 Hz以上的信号精度良好,因此在1Hz以上的频率范围内对稳定杆有限元计算的位移进行校对。如图5~6所示,对比可见2种位移时域波形重叠度良好,PSD曲线分布和数值接近。测试获取的稳定杆端部Z向位移均方根值为4.17 g,基于有限元计算的位移均方根值为4.32 g,比值为1.04 ,基于有限元计算的位移精度良好。

图5 位移谱时域波形局部对比
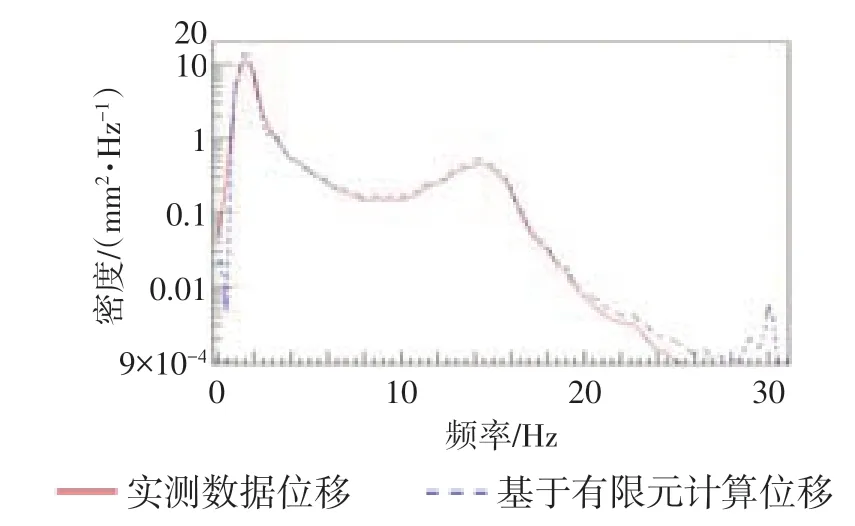
图6 位移谱PSD对比
3 稳定杆吊杆支座动态载荷获取
基于ADAMS.VIEW软件,建立横向稳定杆多体动力学模型,如图7所示。横向稳定杆及其吊杆为刚体,在左右段稳定杆之间建立转动副,并施加等效刚度的扭转弹簧。吊杆与车架连接为球绞,吊杆与横向稳定杆连接为等速副,横向稳定杆与车轮之间采用滑动副和衬套连接。在稳定杆模型两端输入动态Z向位移谱,仿真计算稳定杆吊杆对其支座连接点的Z向载荷谱,如图8所示。
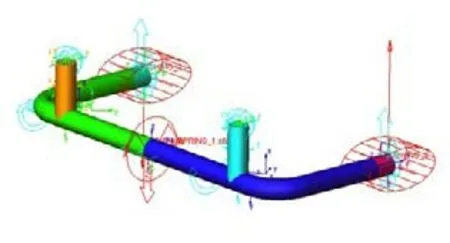
图7 横向稳定杆多体动力学模型

图8 稳定杆吊杆支座连接点的Z向载荷谱仿真图
4 支座及底架结构动应力分析
建立稳定杆支座及底架连接结构的有限元模型,在稳定杆左支座施加单位力进行计算,如图9所示,对应实车载荷谱采集的应变花测点位置的有限元VonMises应力为0.00842 MPa。在支座连接点施加动态载荷谱,采用准静态法计算支座底架结构的全局动应力。如图10~11所示,对应变花测点的实测数据与CAE分析结果进行对比,2种应力谱的时域波形对比结果较好,对应的雨流计数累计曲线分布相似性良好;CAE与实测数据的变程最大值比值为1.13 (小于1.20 )。说明CAE计算得到的动态应力结果精度较好。

图9 单位力下稳定杆支座底架结构的静力计算
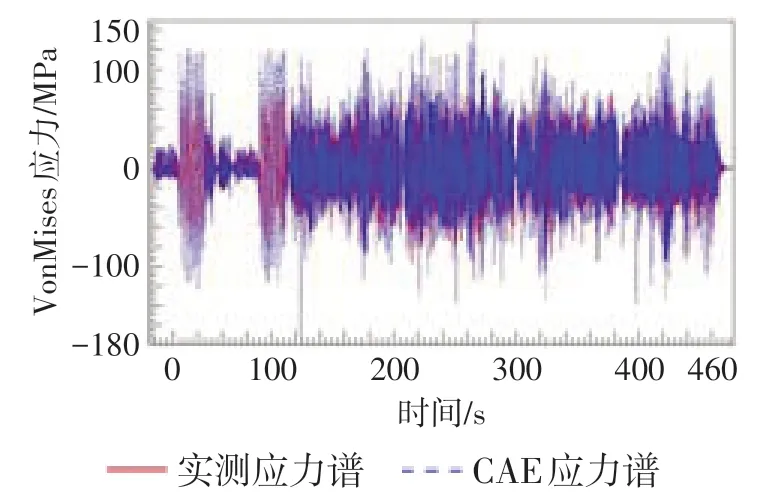
图10 CAE应力谱与实测应力谱对比
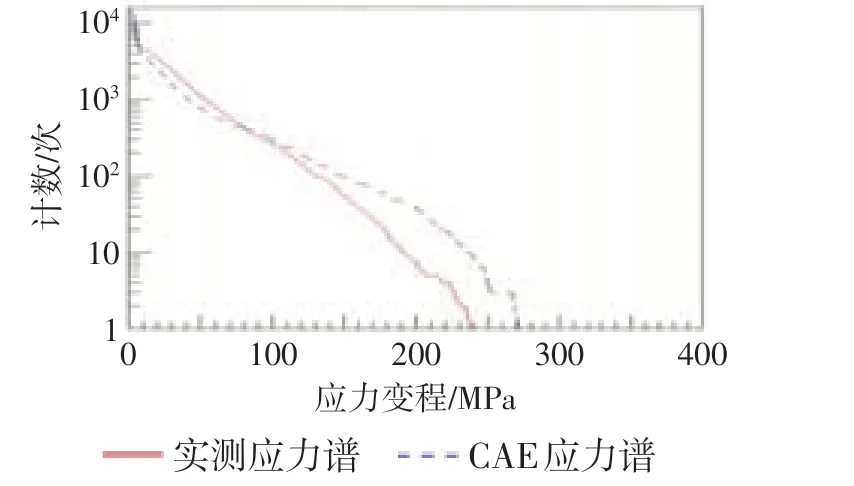
图11 应力谱雨流累计曲线
5 稳定杆支座及底架结构疲劳分析
稳定杆支座底架结构为焊接结构,采用英国的焊接疲劳标准BS7608[6],焊接结构SN曲线方程为

式中:N为焊接结构的疲劳寿命(循环次数);C0为与平均Sr-N曲线相关的数;d为低于平均值的标准偏差数目;σ为logN的标准偏差;m为曲线斜率的倒数;Sr为应力变化范围。d不同,对应的曲线参数不同,若d取0,则对应的SN曲线为平均值SN曲线。文中结构等级为G,C0为5.66 ×1011,m为3。
在BS7608中,以寿命N为107次周期循环为拐点(对应的应力变化范围为S0),此点之前曲线斜率为m的倒数,之后斜率为(m+2)的倒数,具体如下:
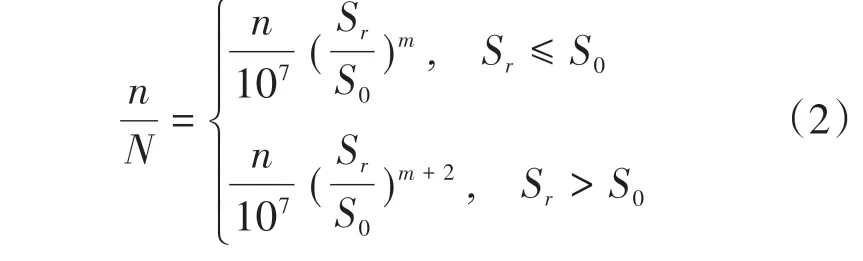
式中:n为被评估点应力变化范围发生次数;S0为对应寿命N为107次循环的应力变化范围。综上,对应焊接结构G等级的Sr-N曲线2段对应关系式为
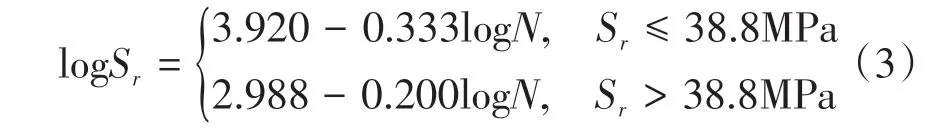
确定好关系式(3)的曲线拐点并处理好2种斜率曲线的连接。在疲劳极限处,循环次数为1.0 ×1011,对应的应力变化范围为6.14 MPa,最终得到全局的SN曲线,如图12所示。
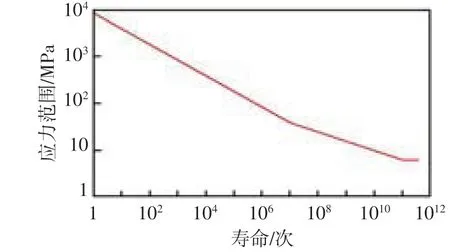
图12 G等级焊接结构SN曲线
在HyperWorks中计算稳定杆支座底架连接结构的疲劳寿命,如图13~14所示。图13中对应测点位置的疲劳损伤计算结果为0.00244,而试验实测载荷谱(图10)利用名义应力寿命法计算该点的疲劳损伤为0.00173,CAE结果相对于试验数据比值为1.41 (小于2且大于0.5 ),说明CAE计算精度良好且存在一定的安全系数。通过该点实测数据损伤验证与分析,保障了CAE全局疲劳分析结果的有效性。图14为全局分析结果,包括支座与底架焊接结构为危险区域等信息,排除焊接应力集中因素,焊接结构最大疲劳损伤为0.00420,最低疲劳寿命里程为2380km,未满足开发要求。

图13 稳定杆左吊杆支座底架结构局部疲劳分析结果
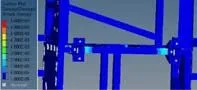
图14 稳定杆吊杆支座底架结构疲劳分析结果
6 结论
通过稳定杆动态应变测试数据,计算稳定杆端部动态位移谱,与加速度测试、转化获得的位移谱在时域波形、频域PSD上的重叠度都良好,均方根比例达到1.04,满足后续的疲劳分析。通过多体动力学和有限元计算,获得稳定杆支座底架动态应力谱,与测试结果相比,2种应力谱的时域波形重叠度良好,雨流计数累计曲线中的变程最大值比值为1.13 ,小于1.20 ,表明文中方法计算的动态应力结果精度良好。CAE与测试相结合,利用焊接结构SN曲线,计算稳定杆支座骨架的疲劳损伤与同处的实测数据的比值为1.41 ,小于2且大于0.5 ,精度达到要求。同时获得焊接结构全局的最大疲劳损伤为0.00420,相应最低疲劳寿命里程为2380km,未满足开发要求,从而明确整改的必要性。
