基于相关性选择的高维多目标优化算法∗

潘晓英 李昂儒 陈雪静 赵 倩

（西安邮电大学计算机学院 西安 710121）

1 引言

在现实生活的许多领域，多目标优化问题较多地涉及到四个以上目标对应的高维多目标优化问题［1］（many objective optimization problems MAPs），如设计的控制器、制造半导体、优化设计等，其共同点在于，它们包含多个目标且之间有冲突。作为经典的多目标优化方法（Multi-objective evolutionary algorithm，MOEA），NSGA2，SPEA2等已成功解决相关问题，但低维优化效果好的算法未能很好解决高维问题，目前研究热点有：1）基于松散Pareto支配关系［4］来提高Pareto非支配排序方法的选择能力，从而提高算法的收敛性能；2）目标降维［2～3］法，通过结合数学方法将目标维数缩减，删除优化问题中的冗余目标，将高维转化为低维问题；3）采用聚合或分解的方法将高维优化问题整合为低维多目标问题求解［5～6］；4）采用不同评价指标的高维多目标优化 算 法（Indicator-based Evolutionary Algorithm，IBEA）［7］的思想是利用评价非支配解优劣的某些指标来衡量个体的优劣程度并进行相应的适应度赋值。其中基于分解思想求解多目标优化问题的MOEA/D［5］算法已经很成功地解决了两个或三个目标的优化问题，它结合数学规划和进化算法，将一个复杂多目标问题分解成若干个单目标优化子问题，然后用进化算法同时求解这些子问题的最优解作为多目标问题的最终解。在这类方法中，拥有显著效果的还有：AMS算法［8］、PPD-MOEA［9］以及 NS⁃GA3［10］算法。通过对上述算法的研究可知，分解方法对解决高维多目标优化问题较好。

在上述基础上，本文提出一种基于相关性选择的多目标优化算法（Correlative selection mecha⁃nism-based evolutionary algorithm for many-objec⁃tive optimization，CSEAM）。在CSEAM算法中，首先在平面上产生一组分布较均匀的参考点，一个参考点决定一条理想点的参考线；如果目标空间中的某个个体离某条参考线的距离比其他参考线都近，那么该参考线对应的参考点就是该个体的相关参考点，对应的个体是该参考线的相关个体。本文算法主要通过给每个参考点至少找到一个相关个体，来保证种群多样性；另外我们会剔除同一参考点下的标量子函数最大的个体，保证种群向理想帕累托前沿方向进行。最后由于CSEAM算法未采用非支配拥挤度排序等庞大的计算方法，在很大程度上可以削减算法的计算复杂度。

2 相关理论背景

2.1 参考点的选择

多目标分解进化算法一般在单位平面上产生一组均匀分布的参考点，一般采用Das和Dennis的方案［11］，该方案在M-1维的单位超平面上均匀产生一组参考点，令M表示优化目标个数，参考点的总数目H是由参数D控制，参数D代表每个目标上划分的份数。用符号组r1，r2，…，rH表示所有参考点，参考点ri（i=1，…，H）中的每一维元素都在中取值，所以ri（i=1，…，H）中的所有元素之和为1。参考点的总数目H和参数D会满足以下式（1）。

以3个目标的多目标优化问题为例（M=3），则参考点将会分布在（1，0，0）、（0，1，0）、（0，0，1）为三个顶点的三角平面上，如果D参数被设定为3，参考点的个数H就为10。如图1，展示了这10个参考点的具体分布情况。但是当目标数M为8时，即使参数P设置为8，那么参考点的总数目H也将会达到5040，这样种群的规模变得非常大或者冗余。为解决参考点总数目H随着M和D急剧上升的问题，在这章中必须应用更加高级的方案，当目标数比较大时，我们采用两层产生参考点的方案。例如对于目标数M为8时，我们在第一层设置参数D=3，根据式（1），则产生120个参考点；在第二层上，我们设置参数D=2，再据式（1），产生36个参考点。故总共产生120+36=156个参考点，远小于原来的个数。

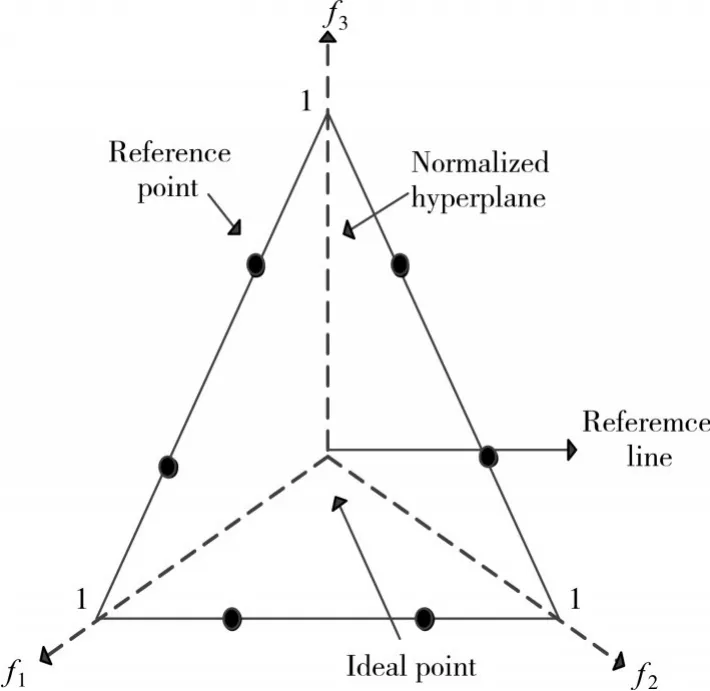
图1 单层参考点分布

图2展示了针对3个目标优化问题应用两层方案产生参考点。对于更多目标数目的优化问题，同样可采用此二层产生方案。

图2 双层参考点分布情况

下面给出两层方案的算法流程，M为优化问题的目标函数的个数；D1表示在第一层中沿每个目标方向划分的份数；D2表示在第二层中沿每个目标方向划分的份数；R1为参考集。如图3。

上述算法中用到的子函数Recursion如图4所示，其中R为参考集（初始化为空集）；r'表示一个M 维的向量，（初始化为0向量）；k代表函数本身的递归次数（初始化为0）；M 为优化问题的目标函数的个数；D表示沿每个目标方向划分的分数；total为参考点r'的前k维元素之和。

图3 两层参考点产生算法流程

图4 Recursion子函数流程

2.2 个体与参考点之间的相关性

图5给出了相关性概念，图中z*和r分别表示理想点和一个参考点。在实际问题中，理想点一般都是未知的，所以一般使用当前出现过的每个目标的最好值作为理想值，即，其中，P表示当前出现过的所有个体解集合；λ=r-z*代表通过理想点z和参考点r的参考线；图中的距离d1表示F（x）在参考线λ上的投影；距离d2表示F（x）到参考线λ的垂直距离。这里的距离 d1、距离 d2分别可以通过式（2）和式（3）计算得来［12］。

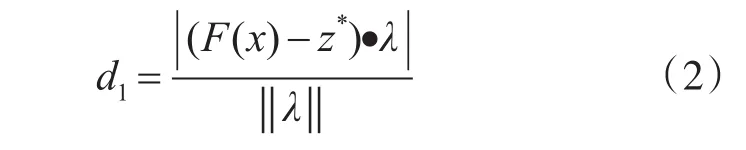
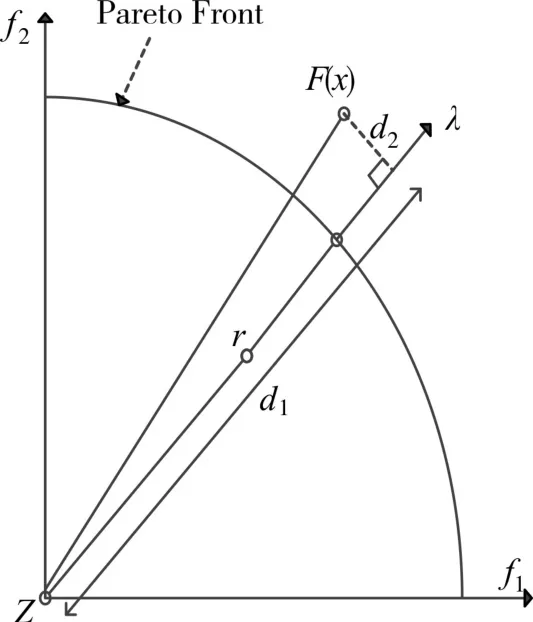
图5 个体与参考点之间相关性说明

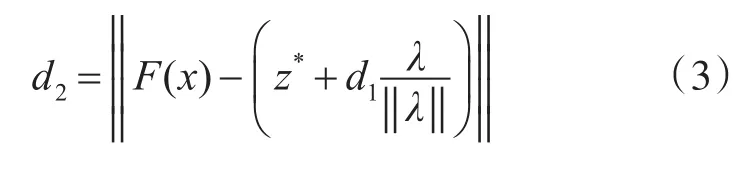
若点F（x）与参考线λ的垂直距离d2比到其他参考线的垂直距离都要小，这时则可定义个体x与参考线λ对应的参考点r成相关性关系，并称个体x是参考点r的相关个体，参考点r是个体x的相关参考点。根据上面定义可以得到每一个个体必须有一个且只能有一个相关参考点，而一个参考点却可以没有或者1个、2个甚至更多的相关个体。

3 基于相关性选择的高维多目标优化算法

3.1 基于相关性的差分进化及多项式变异选择

本节将基于相关性的差分进化及多项式变异选择机制和基于相关性的种群替换机制引入。在详细介绍这两种机制前，先给出每个个体和参考点的相关属性定义。

对于每个个体x，存在3个属性：1）相关参考点rx；2）目标函数F(x)与相关参考点rx对应的参考线之间的垂直距离记为d1x（即图5中的d2）；3）目标函数F(x)与相关参考点rx对应的参考线之间的惩罚距离为d2x=d1+θd2，这里的d1和d2即如图5中的d1和d2，θ为惩罚参数，在实验设置中设置为5，与对比算法MOEA/D中的建议值相同。

对于每个参考点，同样存在3个属性：1）在父代解种群中，参考点r的所有相关个体集合记为Ur；2）在父代解种群中，参考点r的所有相关个体的数目为nr；3）对于参考点r，在所有参考点集中，参考点r最近的T个参考点集Vr，T是固定的参数，在实验中设置为8。

在进行基于相关性的差分进化及多项式变异选择之前，所有个体和参考点的3个属性都会提前被计算好，值得注意的是，每个个体的参考点的属性都是针对当前解种群而言的。图6给出了基于相关性的差分进化及多项式变异选择方法的具体操作过程。

直至得到的后代个体个数满足popsize，则停止算法。因为提出的算法中，个体总数是成双数的，所以种群规模也取为偶数。而在基于分解的进化算法中，种群规模一般和参考点的数目相等，若参考点数目呈奇数，则种群数目就为参考点数目加1；若参考点数目为偶数，则种群数目就为参考点数目。

图6 基于相关性的差分进化及多项式变异选择方法

3.2 基于相关性的种群更新选择

基于相关性的种群更新选择方法，是利用基于相关性的差分进化及多项式变异选择算法所得的子代种群，来更新父代种群的。如图7详细算法流程如下，对于每个子代种群Qt中的第k个个体xk，计算该个体的3个属性，且记为rk、d1xk和d2xk，并且确定其参考点rk的3个属性，分别被记为Urk、nrk和Vrk。

若存在一个个体的参考点rk拥有的相关个体数目为0，则直接将该个体加入到当前父代种群Pt和Urk中，且参考点rk拥有的相关个体数目nrk+1；在找出所有参考点中相关个体的数目最多的参考点rmax；在参考点rmax的所有的相关个体中，找出第3个属性值最大的个体，代表该解的相对收敛性最小，需要将该个体从当前父种群中剔除；最后更新rmax的3个属性。

若不存在参考点的相关个体数目为0，则直接将个体xk加入到当前种群Pt和对应的相关参考点rk的解集Urk中，且相关个体数nrk+1；接着在Urk中，找到第3个属性值惩罚距离最大的个体xmax，并且将它从Pt和Urk中剔除。

通过上述的内容，设定参考点的总数目等于所有参考点相关个体数目之和（或相差为1），这样在搜索时，会出现有的参考点相关个体总数多，有的参考点相关个体总数少或者为0的情况，此时就需要找出相关个体数目最多的参考点，并将该参考点相关个体中的第3个属性值惩罚距离最大的个体从当前种群中删除，以此来保证种群的收敛性。具体算法流程见图7。

图7 算法CSEAM的主要流程

4 实验结果与分析

4.1 DTLZ系列标准多目标优化测试函数

本章采用Deb等提出的DTLZ系列多目标优化测 试 函 数［13～14］来 分 析 CSEAM 的 性 能 ，分 别 为DTLZ1、DTLZ2、DTLZ3和DTLZ4，且这些测试函数在多篇文献中作为标准测试问题用以衡量算法性能，函数详细描述如表4所示。

测试函数，将参数k设置为5，对于DTLZ2、DTLZ3和DTLZ4测试函数，参数k被设置为10。

4.2 评价指标

为了更好地评价算法的收敛性和多样性，这里采用性能指标IGD［15］，在介绍IGD之前，先来了解下指标GD的概念。

GD（Generational Distance）是由V.Veldhuizen和Lamont提出的一种评价方法［16］，用来描述算法所得的非劣解与问题的真是Pareto前沿之间的距离：

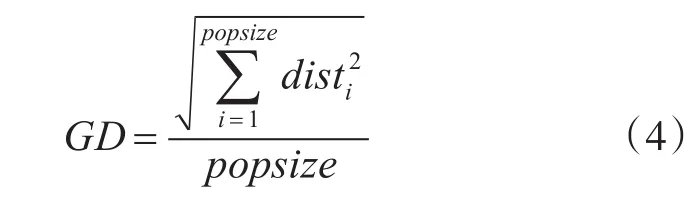
式（4）中，popsize为所求种群PFknown中解数量，disti表示在目标空间中，每一维向量与Pareto前沿PFtrue中的最近向量之间的欧式距离。

表1 DTLZ系列测试问题的数学描述

反代间距离（Inverted generational distance，IGD），表示算法求得的值和理想最优解的趋近差值，设P*为帕累托前沿分布均匀的集合点，P是算法得到的近似Pareto最优解集合。P*到P的平均距离IGD定义为d( )

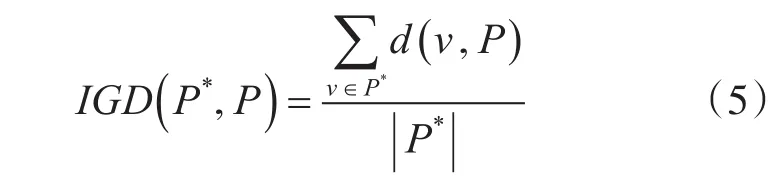
ν，P 是ν与P中所有点的直线距离最小，如果|P*|能达到一定值，IGD从某种程度上代表P的两个性能指标。IGD值越小，表示P与P*的PF越接近

4.3 实验设置

这里将NSGA-III和MOEA/D作为对比算法，因为这两种算法均使用了PBI分解方法。我们使用CDEAM、NSGA-III和MOEA/D来处理表1中的四个测试问题，每种算法分别独立运行30次，取均值来作为算法最终性能，并且比较三者所得结果来分析所提出的CDEAM算法的性能。

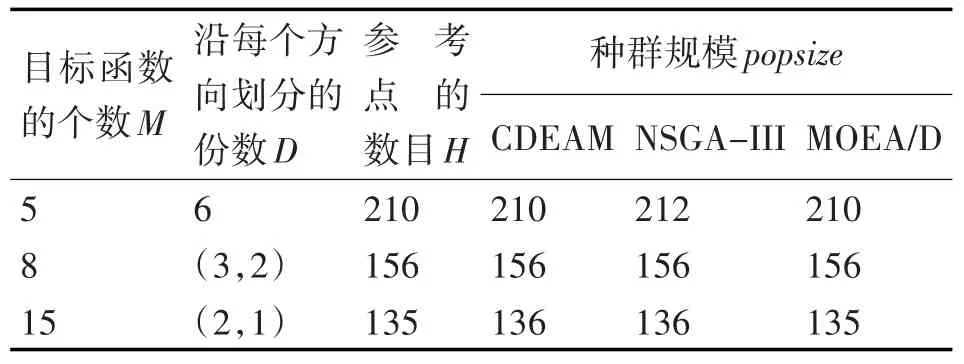
表2 目标函数个数、参考点数目和种群规模参数设置

表2给出了目标函数的个数、参考点的数目和种群规模，表3给出了CDEAM、NSGA-III和MOEA/D的一些其他参数设置。

表3 CDEAM、NSGA-III和MOEA/D的其他参数

4.4 实验结果

对于DTLZ1测试函数，当目标个数为5和8时，IGD值都小于NSGA-III和MOEA/D，而当在目标个数为15时，IGD值大于NSGA-III和MOEA/D，但是IGD值小于MOEA/D。由此可以看出，若目标数小于15维，CSEAM算法的多样性和收敛性的综合性能就要优于NSGA-III，且对于5维、8维、15维，CSEAM的综合效果一直均好于MOEA/D；而对于DTLZ3测试函数的5、8和15维目标下，CSEAM的IGD值均小于NSGA-III和MOEA/D，整体效果要比其他两个算法效果要好；对于DTLZ4测试函数的8维和15维，CSEAM效果均优于NSGA-III和MOEA/D，当目标维数为5时，其效果要差于NSGA-III，但仍优于MOEA/D，所以在较高维的DTLZ4问题上，CSEAM表现较好；对于DTLZ2的5维、8维情况下，算法MOEA/D均稍优于CSEAM，在15维情况下，CSEAM算法IGD值小于MOEA/D，另外5维情况下，NSGA-III的效果稍优于CSEAM，但是对于8维和15维的DTLZ2，CSEAM均远优于NSGA-III，所以对于DTLZ2测试问题，维数越高，CSEAM算法的优势越明显。

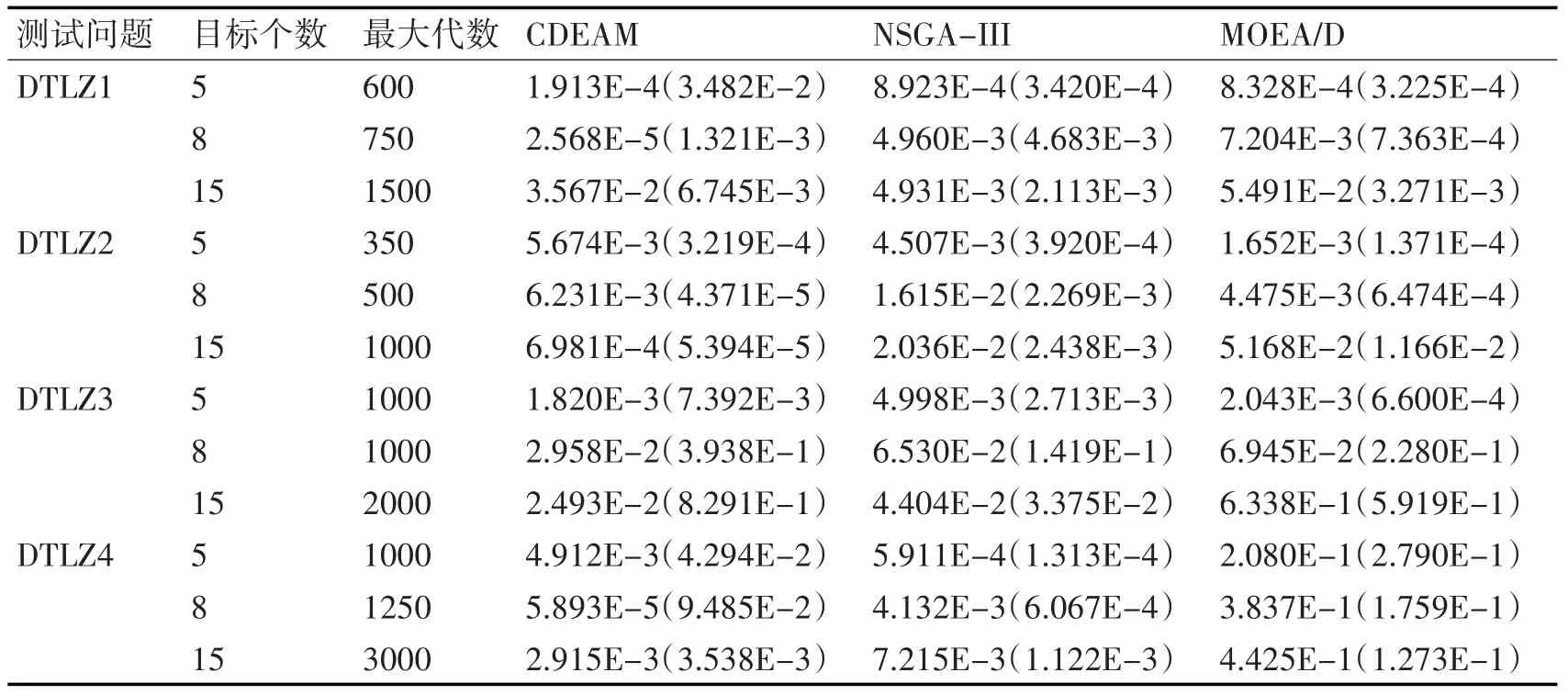
表4 三种算法在DTLZ1-4测试问题上获得的IGD均值和方差

通过实验仿真和分析可得出，本文的算法在几个测试问题的5维、8维和15维上，综合性能均是最好的。其中对于DTLZ1，维数较低较有效；对于DTLZ2，维数较高整体表现较有效；对于DTLZ3，整体性能表现良好；对于DTLZ4，维数越高综合性能越好。

5 结语

本章提出了基于相关性选择的高维多目标优化算法（CSEAM算法），新算法由两部分组成，其中包括基于相关性的差分进化及多项式变异选择，和基于相关性的种群更新选择机制。首先，为清楚的描述相关性选择机制的原理和操作过程，本章给出了个体和参考点相关性的概念，以及参考点的3个属性、个体的3个属性等概念。然后，给出了基于相关性的差分进化及多项式变异选择以及基于相关性的种群更新选择机制的详细算法流程，之后对所提出的算法CSEAM整体流程做了介绍。最后，将CSEAM算法与NSGA-III算法和MOEA/D算法就解决DTLZ1、DTLZ2、DTLZ3和DTLZ4标准测试问题所得的结果进行了对比。通过对所得解集与真实的Pareto解集之间的距离即IGD指标进行分析，验证所提出的算法CSEAM在大部分优化问题上，获得了更优秀的近似解。

［1］K.PRADITWONG AND X.YA.A new multi-objective evolutionary optimization algorithm：The two-archive algo⁃rithm［C］//Guangzhou，China：International Conference on Computational Intelligence.Security，2006：286-291.

［2］X.ZOU，Y.CHEN，M.LIU，AND L.KANG.A new evo⁃lutionary algorithm for solving many-objective optimiza⁃tion problems［J］.IEEE Transactions On Systems，Man，and Cybernetics-Part B，2008，38（5）：1402-1412.

［3］D.K.SAXENA AND K.DEB.Non-linear dimensionality reduction procedures for certain large-dimensional multi-objective optimization problems：Employing corrent⁃ropy and a novel maximum variance unfolding［J］.Evolu⁃tionary Multi-Criterion Optimization，2007，4403（s.n.）：772-787.

［4］Korudu P，Das S，Welch SM.Multi-Objective hybrid PSO using μ-fuzzy dominance［C］.Proc.of the Genetic and Evolutionary Computation Conf，New York：ACM Press，2007.853-860.

［5］Zhang QF，Li H.MOEA/D：A multiobjective evolutionary algorithm based on decomposition［J］.IEEE Trans.on Evolutionary Computation，2007，11（6）：712-731.

［6］Li H，Zhang QF.Multiobjective optimization problems with complicated Pareto sets［J］.MOEA/D and NSGA-II.IEEE Trans.on Evolutionary Computation，2009，13（2）：284-302.

［7］Zitzler E，Brockhoff D，Thiele L.The hypervolume indica⁃tor revisited：On the design of Pareto-compliant indicators via weighted integration［C］.Evolutionary Multi-Criterion Optimization-EMO，Berlin：Springer-Verlag，2007.86-2287.

［8］I.GIAGKIOZIS，R.C.PURSHOUSE，AND P.J.FLEM⁃ING.Generalized decomposition［J］.Evolutionary Multi-Criterion optimization，2013，7811（s.n.）：428-442.

［9］Sato H，Aguirre H E，Tanaka K.Pareto partial dominance MOEA and hybrid archiving strategy included CDAS in many-objective optimization［C］//Evolutionary Computa⁃tion.IEEE，2010：1-8.

［10］K.LI，Q.ZHANG，S.KWONG，et al.Stable Match⁃ing-Based Selection in Evolutionary Multiobjective opti⁃mization［J］.IEEE Transaction on Evolutionary Computa⁃tion，2014，18（6）：909-923.

［11］A.ZHOU，Q.ZHANG，AND G.ZHANG.Aapproxima⁃tion model guided selection for evolutionary multi-objec⁃tive optimization［J］.Evolutionary Multi-Criterion Opti⁃miztion，2013，7811（s.n.）：398-412.

［12］K.DEB，A.SINHA，P.J.KORHONEN，AND J.WAL⁃LENIUS.An interactive evolutionary nulti-objective opti⁃mization method based on progressively approximated value functions［J］.IEEE Transactions on Evolutionary Computation，2010，14（s.n.）：723-739.

［13］K.DEB.Multi-objective optimization using evolutionary algorithms［M］.Chichester，UK：Wiley，2001.1-299.

［14］Q.ZHANG，A.ZHOU，S.Z.ZHAO，P.N.SUGAN⁃THAN，W.LIU，AND S.Tiwari.Multi-objective optimi⁃zation test instances for the cec-2009 special session and competition［M］.Singapore：Nanyang Technological University，Tech.Rep.，2008.

［15］H.Sato，H.Aguirre，and K.Tanaka.Local Dominance Using Polar Coordinates to Enhance Multi-objeetive Evo⁃lutionay Algorithms［J］.Proc.2004 IEEE Congresson Evolutionary Computation，2004，1（s.n.）：188-195.

［16］D A Van Velclhuizen，G B Lamont.Evolutionary Compu⁃tation and Convergence to a Pareto Front［C］.Late Break⁃ing PaPers at the Genetic Programming 1998 Conf，Cali⁃fornia：Stanford Bookstore，1998：221-228.