硝酸盐型卤水体系的综合热力学模型与多温相图预测

王星帆，周 桓，，周 阔，金分丽，杨军芳

(1.天津科技大学海洋与环境学院，

2.化工与材料学院,天津市卤水化工与资源生态利用重点实验室,天津300457)

硝酸盐型卤水存在于天然盐湖、硝酸盐工业过程、电子行业的金属回收液以及煤化工等各类工业废水中，如新疆的硝酸盐型盐湖组成为体系［1］；煤化工综合废水组成为体系；电子线路印刷版的退锡水组成为体系等.硝酸盐具有高溶解度特性，其溶解度可以达到几百mol/kg，在高温下成为熔融状态［2］.

建立精确表达复杂电解质体系物性与固液相平衡的热力学模型是过程开发、模拟、控制的基础.100多年来已形成了Debye-Hückel、离子水化、离子缔合等经典电解质溶液理论及积分方程理论、微扰理论、临界理 论 等近代 电 解 质溶液 理 论［3~5］；而传 统Pitzer与PSC模 型［6，7］、扩展UNIQUAC［8］、eNRTL［9~11］、OLI-MSE［12，13］等半经验模型仍具有处理复杂体系的优势，并被广泛采用和不断发展.

由Chen等［11］改进的eNRTL模型将电解质溶液的非理想性表达为局部构成中“盐对”与“盐对”、“盐对”与水之间的相互作用能.这种作用能与温度的关系用Gibbs-Helmholtz方程表达.模型参数即为作用能在298.15 K的吉布斯自由能增量、生成焓增量和等压摩尔热容增量［14］.在此基础上，Zhou等［15，16］进一步完善了模型方案，提出长程静电作用对称参考态的新表达式，特殊体系非理想性的化学贡献方案；改进了物种热力学参数和液相特征参数获得的多目标综合优化方案.完善后的方案在复杂盐湖卤水体系多温相平衡和多温相图中表现出良好的表达和预测能力.

对于含硝酸盐的水盐体系，宋彭生和黄雪莉等［17~20］开展过大量研究.他们应用原始Pitzer模型，计算了及体系的固液相平衡；也应用早期eNRTL局部组成模型对体系相平衡进行了计算［21，22］，但上述研究仅局限于298.15 K时的溶解度.Clegg等［23］利用PSC模型对本文所涉及体系的物性和相图也进行过详细研究，但温度也局限于298.15 K.体系是我国煤化工行业综合水处理过程形成的典型体系.综合水先后经过电渗析（ED）或机械蒸汽再压缩（MVR）蒸发浓缩、多效蒸盐硝分离、冷冻减除硫酸钠和高温蒸发固化等过程，最终实现废水零排放.该过程组分多，浓度和温范围宽，尤其是硝酸盐的浓度在高温下可以达到几百mol，对精准表达物性和多温相平衡计算的热力学模型要求高.关于体系热力学的相关研究汇总在表S1（本文支持信息）中.由表S1可知，该四元体系多温和全浓度范围的热力学研究尚未见报道.

本文系统总结了改进后综合热力学模型的要点，并应用于含硝酸盐的多温复杂体系.通过对二元体系、三元体系物性和相平衡的表达，获得液相特征参数和固相物种的热力学参数，进而预测四元体系的多温物性和完整相图.由此获得了具有足够精度的硝酸盐体系多温模型.该研究拓展了电解质模型对复杂体系在超浓和多温过程的表达能力，为硝酸盐体系及煤化工废水处理的过程提供了通用的热力学模型.

1 热力学模型框架

1.1 过剩吉布斯自由能与活度系数

电解质水溶液体系的非理想性，用过剩的吉布斯自由能Gex来表达，在eNRTL模型［9~11］中Gex考虑了长程静电贡献和短程作用贡献，即

式中：长程静电贡献Gex，PDH采用Pitzer-Debye-Hückel（PDH）模型；短程作用贡献Gex，1c采用局部构成（lc）的Non-Random Two Liquids（NRTL，非随机两流体）模型.溶液中各组分的活度系数由过剩的吉布斯自由能Gex导出，即

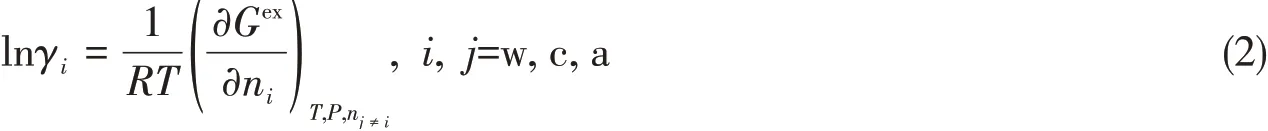
式中：γi是组分i的活度系数；ni为组分i的摩尔数；w，c，a分别为水溶液组分的水、阳离子和阴离子.

组分i基于摩尔分数xi的活度系数γx，i与基于摩尔浓度mi的活度系数γm，i之间的关系为

或者

式中：xw是水在溶液中的摩尔分数；Mw为水的相对分子量.

1.2 多元电解质水溶液体系的对称参考态

利用式（2），由Gex得到活度系数时，需要指定参考态.在原始电解质溶液理论中，水的参考态为纯水，即

离子组分的参考态为无限稀释状态，即非对称参考态：

采用上述参考态且采用摩尔浓度在表达高浓度水盐体系时会受到限制，如经典的Pitzer模型适宜浓度不超过6 mol/kg.研究涉及的硝酸钠溶解度在543.15 K时达到226.88 mol/kg.因此结合NRTL模型的特点，对于高浓度体系，浓度采用摩尔分数，离子组分参考态采用理想的熔盐对称参考态是必要的.对比Pitzer模型［6］的单电解质参考态和Chen等［9］的理想熔盐参考态，提出了多元电解质体系的新参考态表达式［15］，即

式中：Ix是基于摩尔分数的离子强度是Ix在无水的理想熔盐状态的离子强度，即

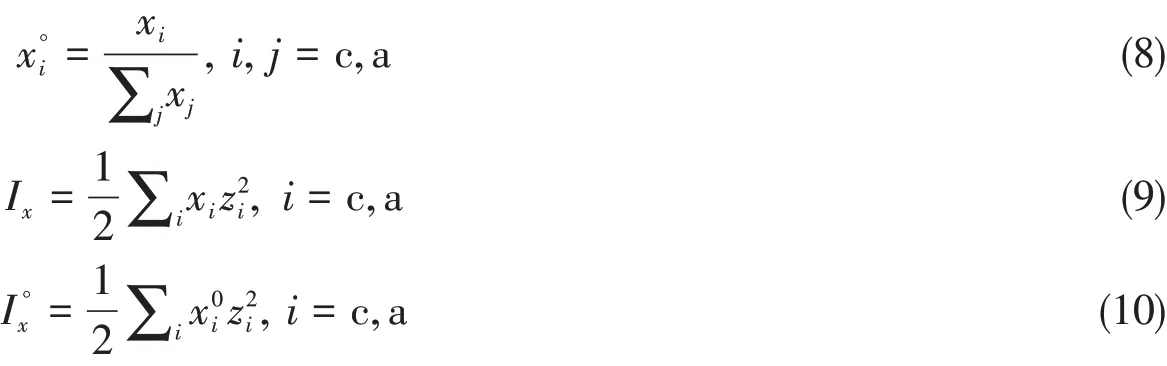
1.3 对称参考态PDH项活度系数的多温表达

基于式（7）的对称参考态，重新推导PDH项的水和离子的活度系数表达式：

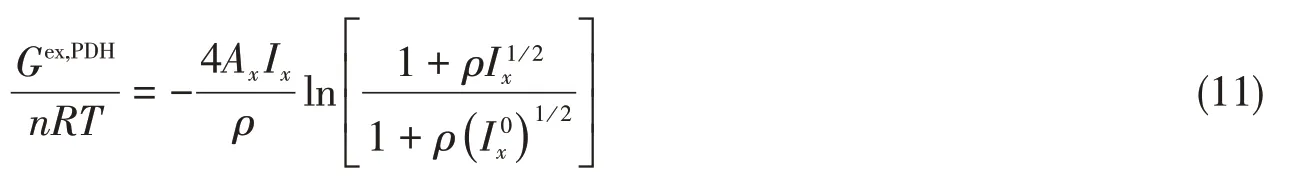
利用式（2）和对称参考态［式（7）］对式（11）求导得到：

式中：Ax是基于摩尔分数的Debye-Hückel参数：

PDH项受温度的影响表现为Ax与温度的关系：一是式（14）包含T；二是温度对水密度(dw)和介电常数(ε)的影响.本文采用文献［24，25］的表达式，即

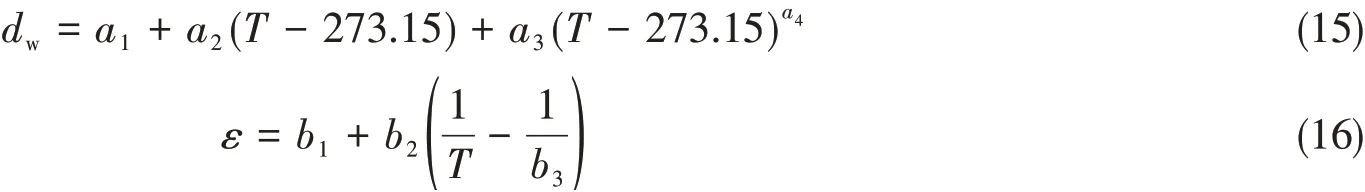
式中：水密度dw及温度常数a1~a3分别为0.99965，2.0438×10−4，6.1744×10−5和1.5［24］；介电常数的温度常数b1~b3分别为78.54，31989.4和298.15［25］.

式（11）~式（14）中，ρ为校正参数，按Pitzer模型［26］的处理方法，设定为14.9.

其中

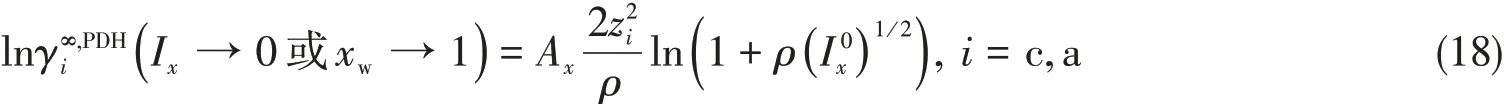
1.4 NRTL贡献项与液相特征参数

过剩吉布斯自由能的短程贡献Gex，lc，以NRTL理论为基础，并考虑电解质体系同性离子互斥和局部电中性的原则.电解质溶液由溶剂分子和离子组成，并形成分别以溶剂分子m、阳离子c和阴离子a为中心的三类局部构成，由局部构成统计计算组分之间作用对过剩吉布斯自由能的贡献，可表达为

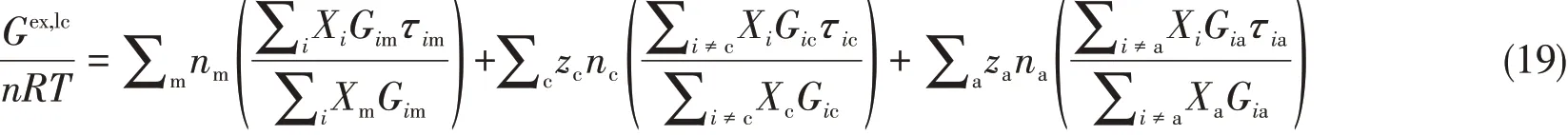
式中：Xi表达局部构成，其计算方法如下：

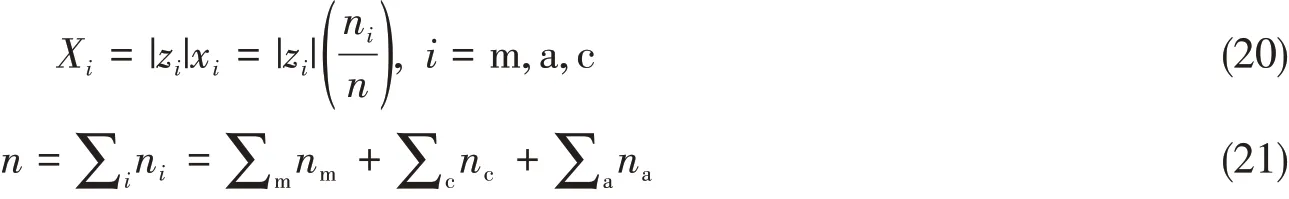
式（19）中，Gij是各组分（i，j）之间的相互作用参数τij所产生的吉布斯自由能：

式中：τij是溶液组分（溶剂分子、阴阳离子）之间的相互作用参数；αij为随机因子，取值为0.2.

eNRTL模型将离子考虑为盐对形式，以满足局部电中性的要求.而基于盐对形式的相互作用能GIJ与基于离子形式的局部构成作用能Gij之间的关系为

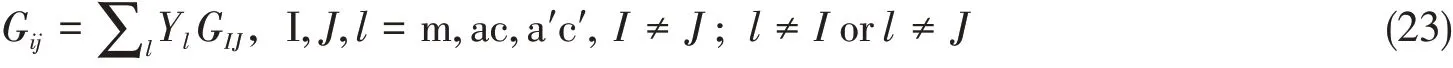
式中：Yl是混合规则，其计算过程详见文献［11，15］.基于“盐对”形式的作用能GIJ，由基于“盐对”的作用参数τIJ来表达，即

式中：τIJ是eNRTL模型中表达液相非理想性的作用参数，具有能量属性，与温度有弱的相关性［14］，可以用类似吉布斯霍姆霍斯方程来表达：

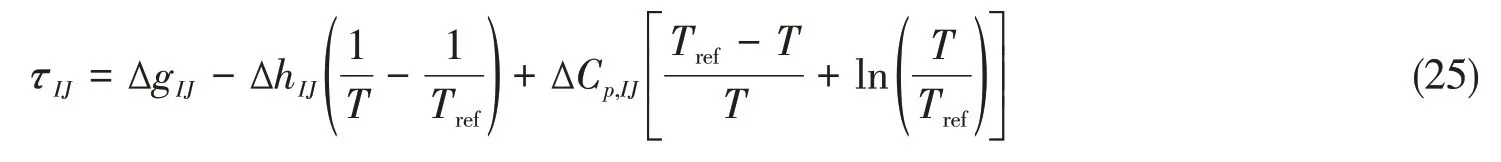
式中：ΔgIJ是二元组（I J）交互作用τIJ的首参数，代表参考温度Tref=298.15 K下，交互作用能形成的吉布斯自由能增量；ΔhIJ和ΔCp，IJ是交互作用的多温预测参数，分别代表生成焓增量和等压摩尔热容增量.这3个参数就是表达溶液非理想性及其多温规律的液相特征参数，均与温度无关，其中ΔgIJ和ΔCp，IJ无量纲，ΔhIJ单位为K−1.研究所得体系的液相特征参数见表1.

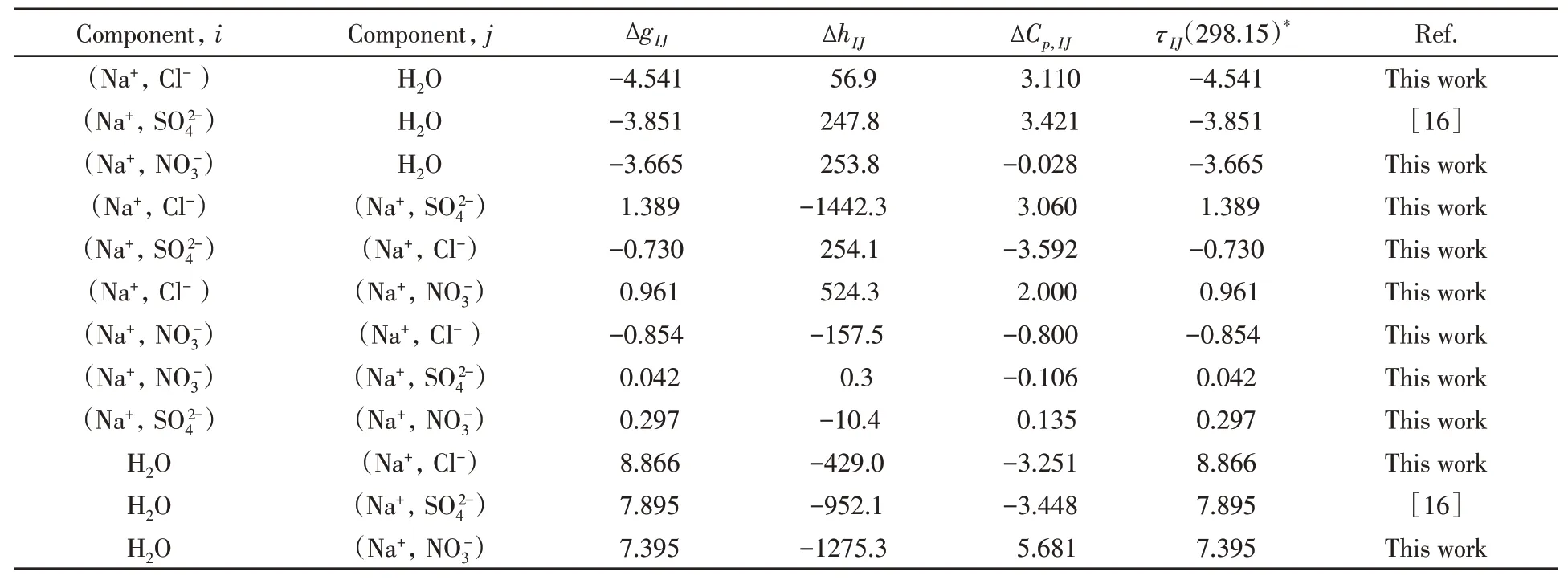
Table 1 Liquid parameters for NaNO3⁃NaCl⁃Na2SO4⁃H2O aqueous system

1.5 多温固液相平衡与固相物种参数

固液相平衡判据是某盐k的离子活度积Asp，k等于活度积常数Ksp，k，即

其中

式中：Asp，k和Ksp，k是给定固体盐k的活度积和活度积常数，k=Mv+Xv−·nH2O；mi，γm，i是液相中离子组分i的摩尔浓度和活度系数；vi，k是固体盐k的化学计量系数；是温度T时的标准生成吉布斯自由能.通过Gibbs-Helmholtz方程计算［4］：

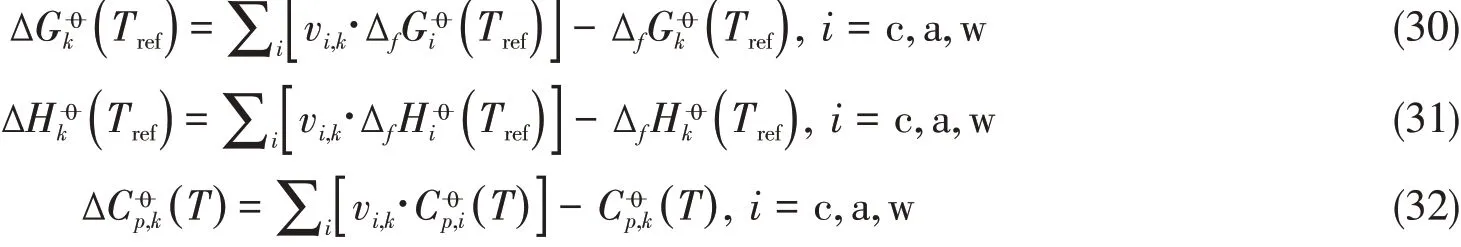
Table 2 Thermodynamic constants of liquid species for Na+-aqueous system

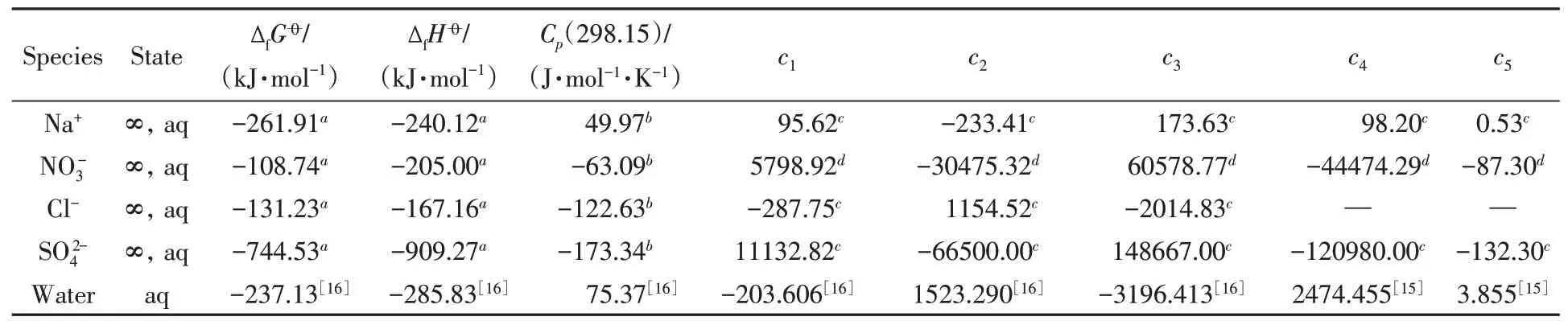
Table 2 Thermodynamic constants of liquid species for Na+-aqueous system

a.Thermodynamic values for ions were taken from NBS table［27］；b.Cp for ions and water adopted in this study was Cp（T）=c1+c2t+c3t2+c4t+c5t−2，t=−T×10−3［28］；c.thermodynamic values were determined from this work along with aqueous NaCl，LiCl，KCl，Na2SO4 binary systems；d.ther⁃modynamic values were determined from this work along with aqueous NaNO3 binary system.

?

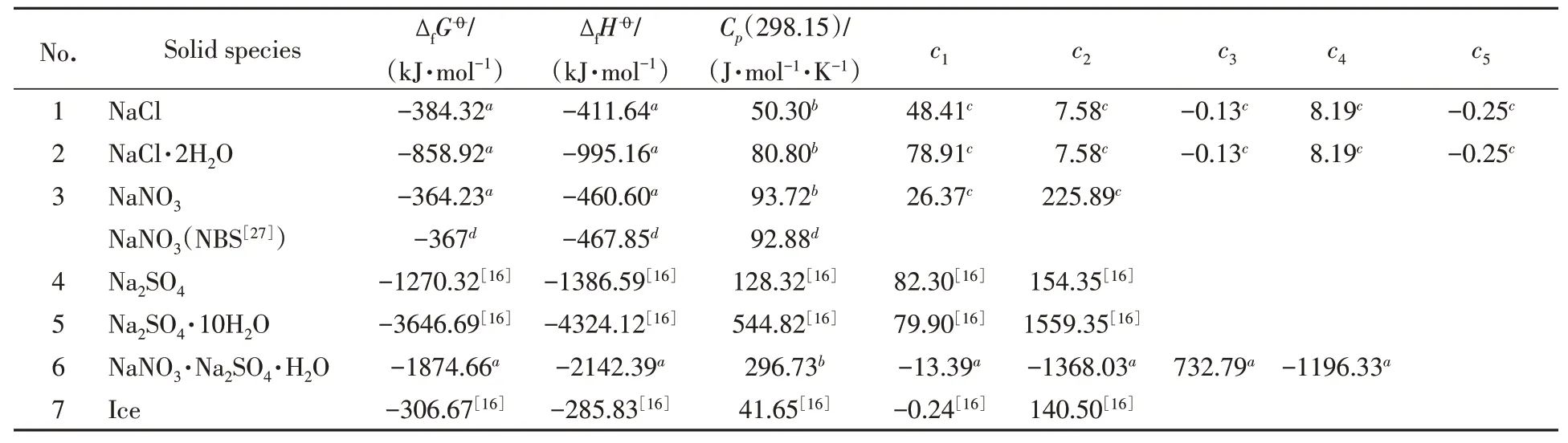
Table 3 Thermodynamic data of solid species in NaNO3⁃NaCl⁃Na2SO4⁃H2O system

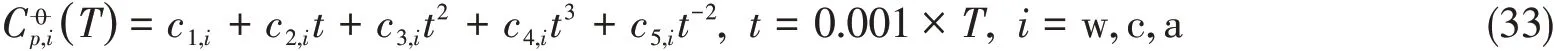
式中：水的参数c1−5，i为NIST数据［28］，数据为本文研究结果，其它离子为已有结果［15，16］，详见表2.对于固相物种采用无机化学手册［29］推荐的三参数表达式，即

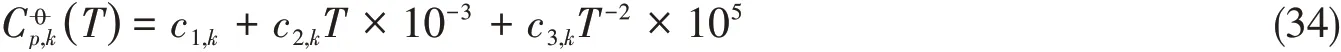
式中：参数c1−3，k以无机化学手册数据［29］为参考并依据固液相平衡进行优化，优化后数据详见表3.

1.6 参数化方案

模型参数包括液相参数和固相参数.其中液相特征参数为盐对与水，或盐对之间的ΔgIJ，ΔhIJ，和ΔCp，IJ；固相参数为待优化的物种热力学常数和固相等压摩尔热容的温度系数.

液相特征参数的盐对-水的作用参数，采用二元体系溶液物性数据：饱和蒸汽压、比热和冰点等作为目标函数进行多目标拟合，盐对-盐对作用参数采用三元体系等温固液相平衡数据的多温拟合得到，其中溶液物性模型见文献［15，16］.二元体系的固相参数通过二元体系多温固液相平衡数据拟合获得.复盐的多元固相参数由相应体系该盐的多温相平衡数据拟合得到.模型参数确定的多目标优化方案为

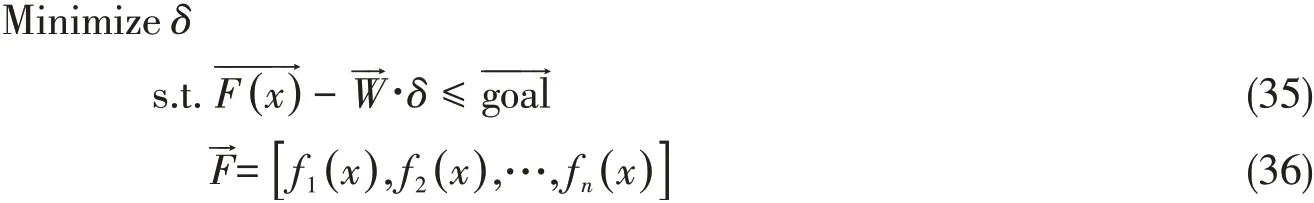
式中：δ是虚拟变量；分别是目标函数计算值和目标值；fn(x)是物性计算函数，参见文献［15，16］；是目标权重，目标函数计算值和目标值之间的平均相对偏差（MRD，%），计算如下：

式中：k是数据的点数；Est表示模型计算值；Exp表示实验值.

2 结果与讨论

2.1 溶液物性与液相特征参数

液相特征参数是盐对-水、盐对-盐对之间作用的温度系数.盐对-水之间的作用参数利用二元体系物性的拟合来获得.重点给出NaNO3-H2O二元体系的物性与液相特征参数，其它两个体系见文献［16，30］.NaNO3-H2O体系的物性数据包括活度系数、渗透系数、饱和蒸汽压、冰点、等压摩尔热容等文献数据，汇总于表S2（本文支持信息）中.

模型及液相参数对物性的表达：离子平均活度系数见图S1（本文支持信息），在298.15 K和浓度从0.001 mol/kg到10.83 mol/kg范围内，模型计算结果与Hamer等［31］的实验数据误差的MRD仅为0.32%.

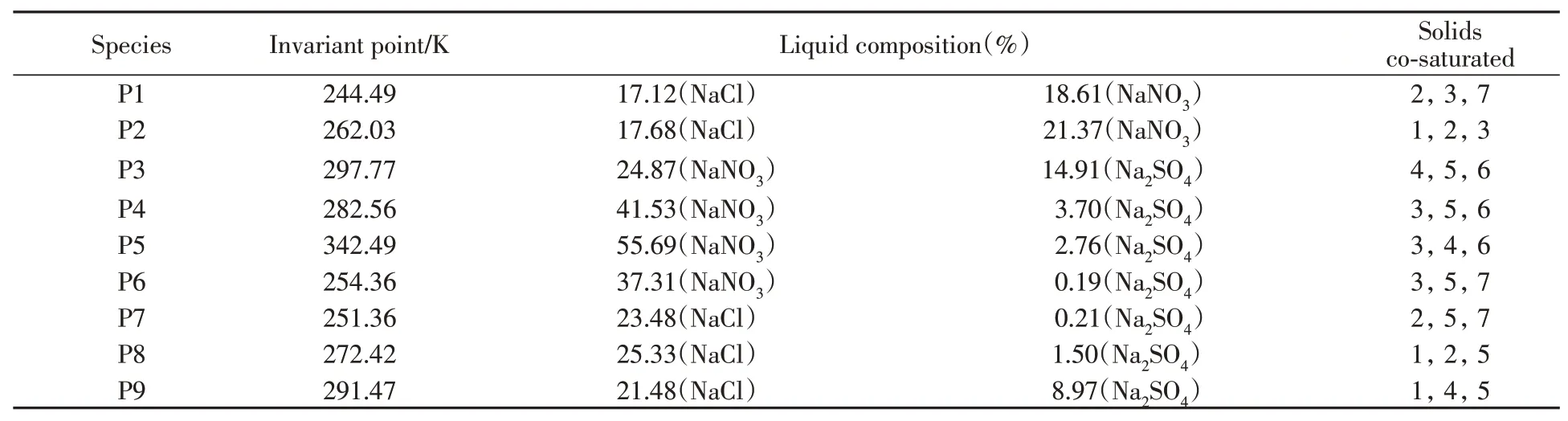
Table 4 Invariant points in the ternary systems of this work*

硝酸钠溶液饱和蒸汽压：由表S2和图S2（本文支持信息）可见，模型计算值与Apelblat等［33］的硝酸钠饱和溶液蒸汽压（温度：277.65~323.15 K）实验值差异的MRD为1.74%；与Zaytsev等［34］的蒸汽压数据（温度：273.15~623.15 K，浓度：0.62~25.00 mol/kg）差异的MRD为2.32%.由此可见，本模型和参数能够很好地表达NaNO3-H2O体系多温及浓度至饱和的蒸汽压.表S2中与Dingemans等［32］的模拟数据比对，表明在高温高浓度范围，Dingemans模型的偏差较大.

溶液的等压摩尔热容：溶液的等压摩尔热容是溶剂、离子等物种的等压摩尔热容的总和，并叠加了组分活度系数的影响.各组分活度系数对溶液等压摩尔热容的影响，取决于作用参数的温度系数ΔhIJ和ΔCp，IJ.等压摩尔热容计算结果与实验值的对比见图S3（本文支持信息）.其中Zaytsev等［34］汇总的等压摩尔热容数据，覆盖了温度从278.15~423.15 K，浓度从0.24~11.77 mol/kg的范围，其总体MRD为0.45%.由此可见，模型和参数能够精确地表达NaNO3-H2O体系在较宽的浓度和温度范围的等压摩尔热容.

冰点是低温范围溶液的重要物性，反映了水在低温条件下的活度特性.图1绘制了3个二元体系冰点数据与计算结果的对比.由图1可见，NaNO3-H2O冰点的模型数据与Deng［35］报道的数据非常吻合，而Jitka等［2］汇总的冰点数据质量不高，是表S2中偏差大的主要原因.

溶液渗透系数：计算值与文献值比较的MRD见表S2和图S4（本文支持信息）.由图S4可知，4组不同来源的数据涉及较宽的温度和浓度，由于不同数据的偏差分布很大，无法用渗透系数的拟合获得液相特征参数.在本文中，渗透系数仅作为计算效果的对比.

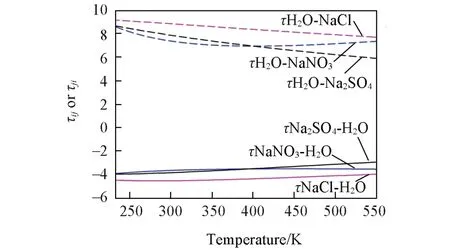
Fig.2 Temperature dependence of eNRTL binary interaction parameters for NaNO3,NaCl,Na2SO4 aqueous binary systems

2.2 二元体系固液相平衡与固相参数

9组NaNO3-H2O体系的溶解度数据汇总于表S3（本文支持信息）中.在254.65~582.65 K区间内，固相只有NaNO3和冰.硝酸钠在水中溶解度很大，尤其在高温范围，溶解度随温度的增加急剧升高（图3）.298.15 K时，NaNO3的饱和浓度为10.79 mol/kg，在543.15 K时，饱和浓度上升到226.88 mol/kg，在582.65 K时，NaNO3达到熔点温度，硝酸钠的摩尔分数达到100%.

当液相特征参数和液相物种参数确定后，表达NaNO3溶解度的可调参数只有固相物种的和等压摩尔热容可以通过溶解度数据确定饱和固相的物种参数.具体拟合过程：固定的温度系数（化工手册数据［29］）.采用Jitka等［2］，Benrath等［36］，Liu等［37］，Niu等［35］，Kracek等［38］和Seidell等［39］在254.65~582.65 K区间内得到的溶解度数据拟合NaNO3的（见表2）.溶解度计算结果见图3，与Jitka等［2］报道的溶解度数据（温度为254.65~543.15 K，浓度为0~226.88 mol/kg），计算MRD仅为1.96%.据此得到NaNO3在298.15 K下标准状态下的热力学常数分别为−364.23和−460.60 kJ/mol，与文献［40］一致，虽然略高于NBS［27］手册数据，但其更适用于宽泛的温度和浓度范围.

冰和NaNO3（s）共饱的二元零变量点计算结果的温度为251.27 K，浓度为8.72 mol/kg.

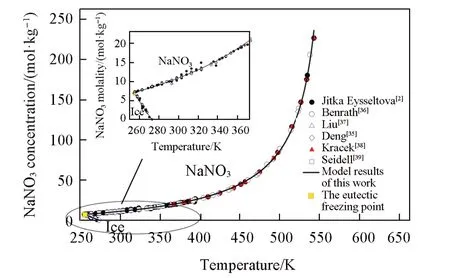
Fig.3 Solubility simulation curve and local enlarged diagram(inset)of NaNO3⁃H2O binary system at the temperature range of 254.65―543.15 K

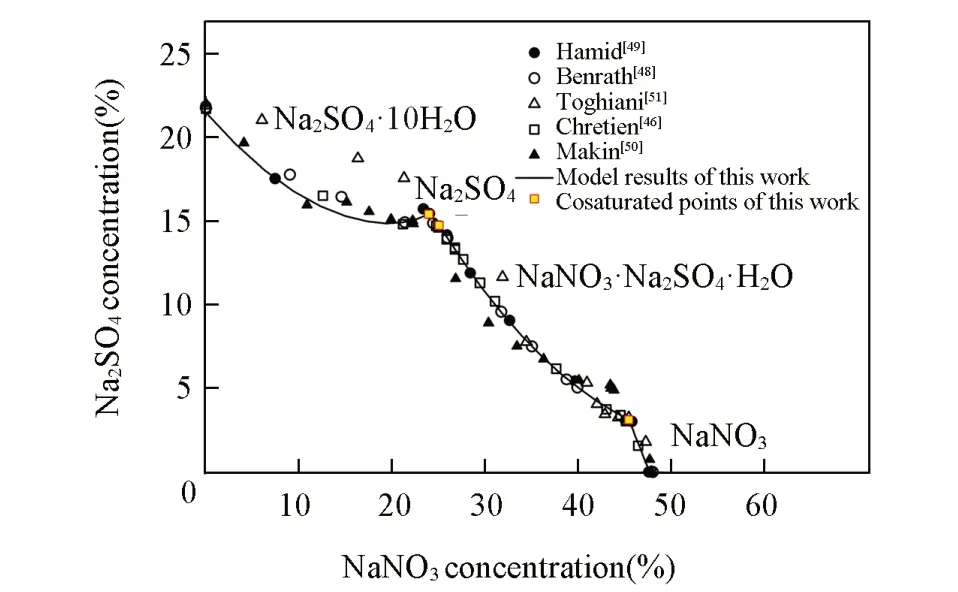
Fig.4 Solubility of NaNO3⁃Na2SO4⁃H2O system at 298.15 K

2.3 三元体系液相与固相参数

Na+//四元体系包含3个三元体系，其中含硝酸盐的NaNO3-NaCl-H2O和NaNO3-Na2SO4-H2O的溶解度数据分别汇总在表S4和表S5（本文支持信息）中.三元体系的液相特征参数（ΔgIJ，ΔhIJ，ΔCp，IJ），即等盐对作用参数，可通过三元体系的固液相平衡数据拟合得到.具体方法：如盐对的交互作用参数，首先用已知298.15 K下的固相Na2SO4⋅10H2O和NaNO3的等温相图数据（图4），拟合τIJ的首参数ΔgIJ；再用多温溶解度数据，拟合多温预测参数ΔhIJ和ΔCp，IJ.

将Hara等［41］，Holzl等［42］，Leather等［43］，曹晶［44］，Cornec等［45］，Chretien［46］报道NaNO3-NaCl-H2O体系的溶解度（表S4，本文支持信息，温度范围为263.15~378.15 K）；Chretien［46］，Massink［47］，Benrath［48］，曹晶［44］，Hamid［49］，Makin［50］，Toghiani等［51］报道的NaNO3-Na2SO4-H2O溶解度（表S5，本文支持信息，温度范围273.15~373.15 K）分别用于拟合这两个体系的液相参数，结果见表1.

两个三元体系不同温度相平衡的表达效果，在此仅给出了298.15和373.15K相图［图4和图S5~图S7（本文支持信息）］.其中，NaNO3-NaCl-H2O体系在298.15~373.15 K区间的等温相图没有复盐，计算与实验数据拟合相对较好.NaNO3-Na2SO4-H2O体系在298.15~373.15 K区间的相图数据比较分散，且出现了复盐NaNO3⋅Na2SO4⋅H2O的相区.计算结果很好地表达了实验结果的总趋势，由此可以判定或评估实验数据的质量，如Toghiani等［51］的数据显然偏差较大.

3 相图预测

3.1 三元体系相图预测

三元体系多温零变量点很难通过实验测定，三元体系完整的相区结构也不能用实验数据准确划分.为此，可利用综合热力学模型，预测两盐共饱的多温曲线及三盐共饱的零变量点，从而确定三元体系相图的完整结构；对于四元体系，没有四元体系新参数，相平衡和相图计算均基于二、三元体系参数来计算.

对三元完整相图的预测，采用了两种方法：（1）利用吉布斯自由能最小法确定三元零变量点，而后在零变量点之间建立单变量曲线；（2）采用推演方法，二元体系或三元体系的零变量点出发，增加另一种盐，直至新盐饱和的计算方法.3个三元体系零变量点的预测结果汇总于表4中.

NaNO3-NaCl-H2O体系从最低共熔点244.49 K到373.15 K下的完整结构相图见图5，可见等温溶解度曲线与实验数据非常吻合；预测所得两盐共饱线和三盐共饱点，给出了4个固体盐（NaNO3，NaCl，NaCl⋅2H2O和冰）对应的饱和曲面.以干基摩尔分数x（%）=［m（NaNO3）］/［m（NaNO3）+m（NaCl）］为横坐标，温度为纵坐标，对单变量曲线和零变量点作图，得到的多温相图见图6.该图给出了每个固体盐所对应的组成和温度范围.其中两盐共饱线和三盐共饱的零变量点的预测结果，表达了4个文献数据的总趋势.预测得到该体系的最低共熔点P1是244.49 K的NaNO3、NaCl⋅2H2O和冰的共饱点.

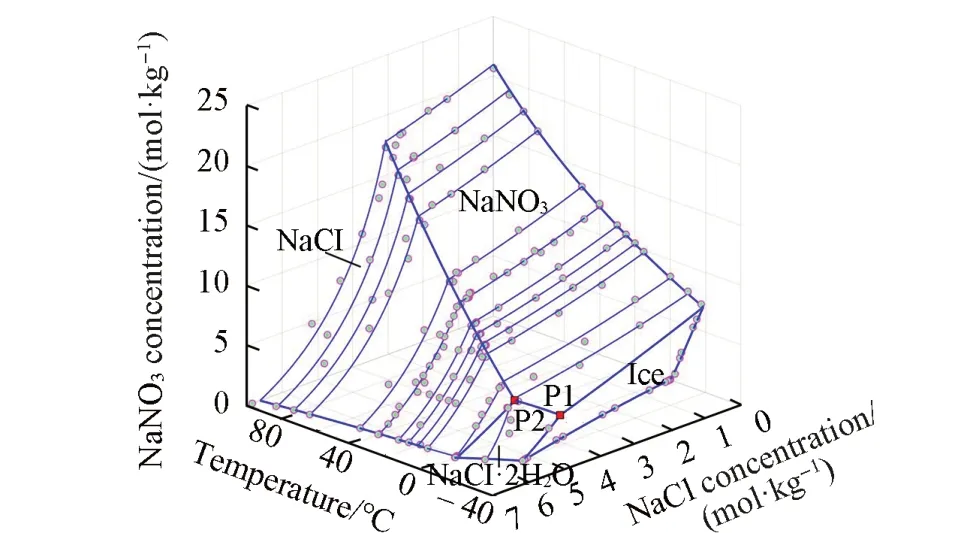
Fig.5 Predicted complete structure 3D phase diagram of NaNO3⁃NaCl⁃H2O system

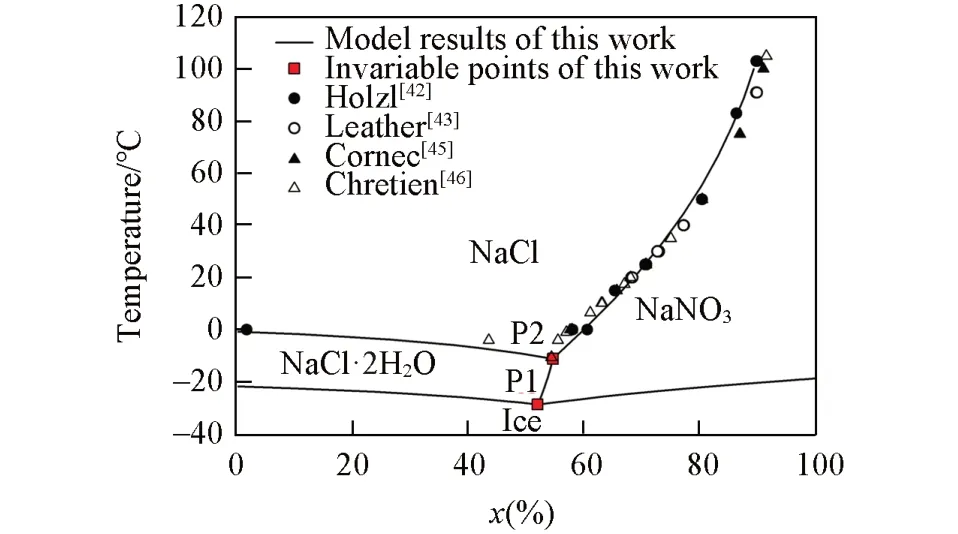
Fig.6 Predicted polythermal phase diagram of NaNO3⁃NaCl⁃H2O system

NaNO3-Na2SO4-H2O体系的完整相图预测及等温相图计算结果见图7，多温相图见图8.该体系5个固相，8条两盐共饱线，4个零变量点.最低共熔点P6计算结果为254.36 K.由图6和图8可见，单变量曲线和三盐共饱的零变量点的预测值，表达了6组文献数据的总趋势；复盐NaNO3⋅Na2SO4⋅H2O相区恰好是NaNO3，Na2SO4和Na2SO4⋅10H2O 3个固相区域交割所产生的区域.

NaCl-Na2SO4-H2O体系在251.36~423.15 K范围内有5个固体盐，完整结构相图和多温相图的预测结果见图S8和图S9（本文支持信息），与实验数据也非常吻合.

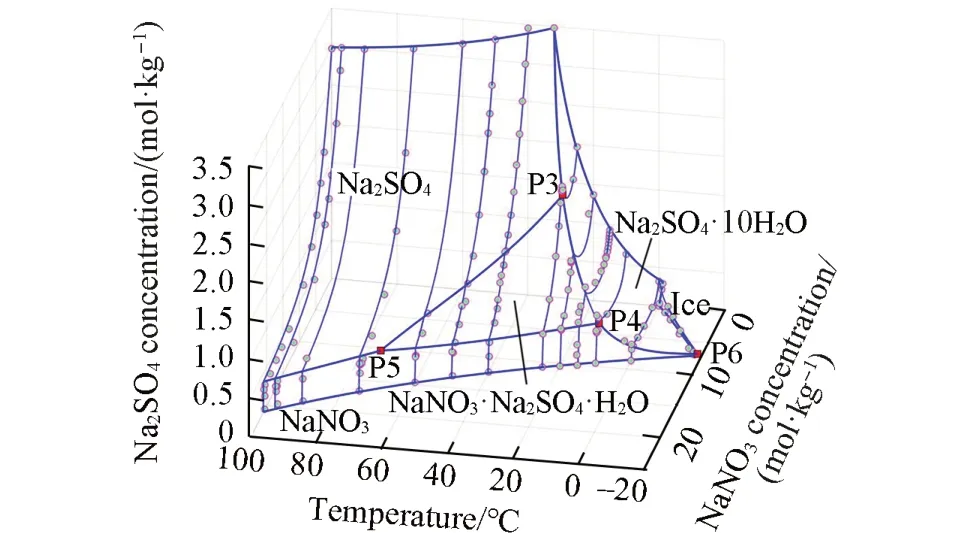
Fig.7 Predicted complete structure 3D phase diagram of NaNO3⁃Na2SO4⁃H2O system

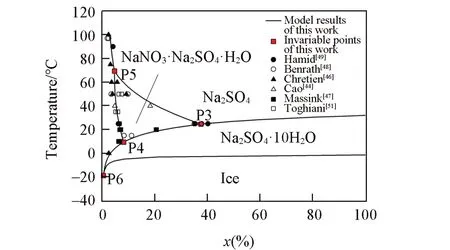
Fig.8 Predicted polythermal phase diagram of NaNO3⁃Na2SO4⁃H2O system

3.2 四元体系相图预测

利用二、三元体系获得液相及固相参数，对NaNO3-NaCl-Na2SO4-H2O体系相图数据（表S6，见本文支持信息）进行对比计算，298.15 K等温相图预测结果与文献数据的比较见图9，水图见图10［横坐标x（%）=m（NaNO3）/［m（NaNO3）+m（NaCl）］，纵坐标为水的百分含量］.其它温度313.15，348.15和373.15 K等温相图和水图的预测结果分别见图S10~图S15（本文支持信息）.可见，在每个温度下，无论是干基图还是水图的预测结果都与文献数据吻合得很好.由此可以判断，图S8中313.15 K的水图数据的计算值与实验值的偏差，可能是实验数据存在误差.

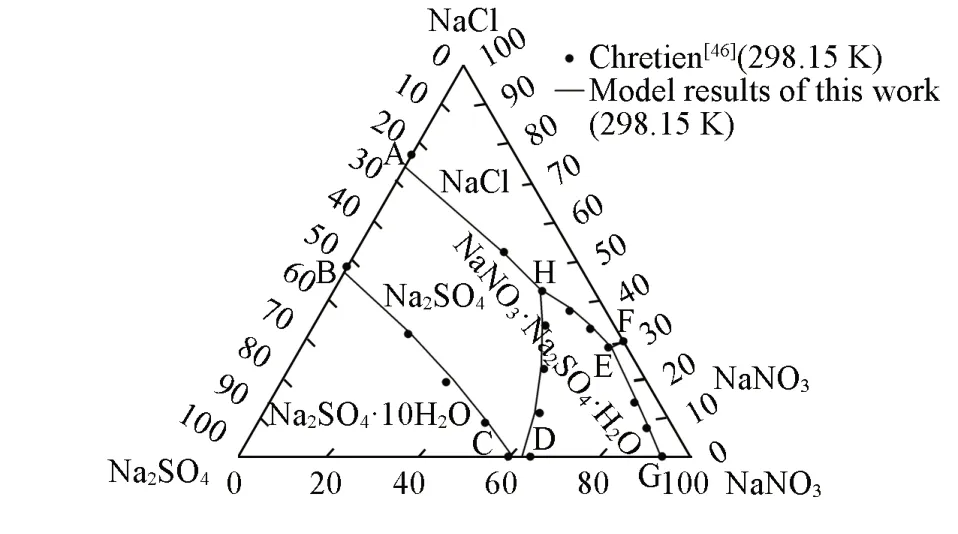
Fig.9 Predicted phase diagram of NaNO3⁃NaCl⁃Na2SO4⁃H2O system at 298.15 K

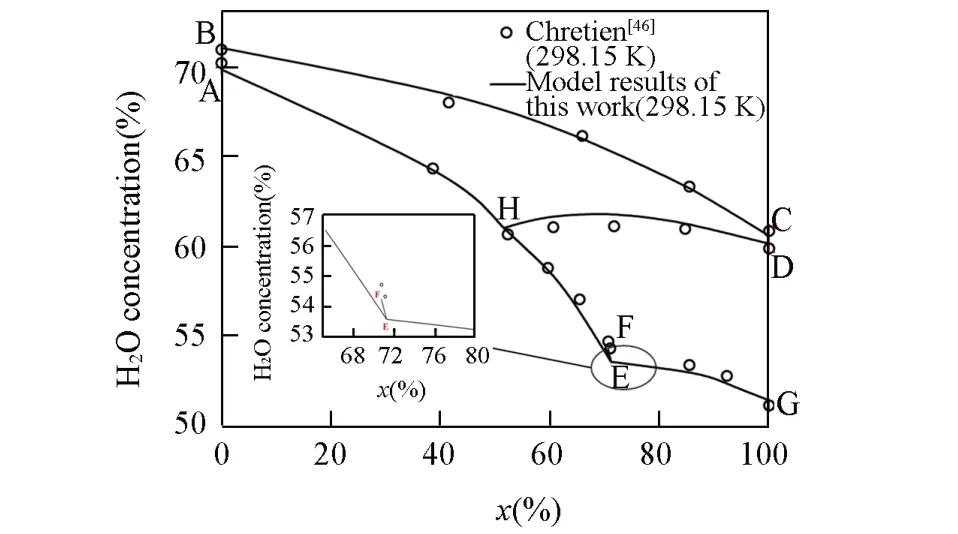
Fig.10 Water diagram of NaNO3⁃NaCl⁃Na2SO4⁃H2O system at 298.15 K

Table 5 Invariant points in system of this work*

Table 5 Invariant points in system of this work*

*1.NaCl；2.NaCl·2H2O；3.NaNO3；4.Na2SO4；5.Na2SO4·10H2O；6.NaNO3·Na2SO4·H2O；7.Ice.

?

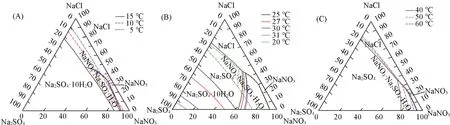
Fig.11 Predicted polythermal phase diagrams of NaNO3⁃NaCl⁃Na2SO4⁃H2O system at different temperatures

综上所述，本文针对硝酸盐型卤水具有溶解度高、工业过程多温和组分浓度变化大的特点，选择体系开展热力学综合模型的构建和复杂体系多温完整相图的预测研究.以eNRTL活度系数模型为基础，建立了活度系数模型、溶液物性模型、物种热力学模型和固液相平衡模型等综合热力学模型；提出了活度系数长程静电项的对称参考态和新表达式；用Gibbs-Helmholtz方程表达局部构成的盐对之间，盐对与水之间作用的温度特性；液相特征参数具有明确物理意义，分别对应吉布斯自由能增量、生成焓增量和等压摩尔热容增量.通过对溶液物性的饱和蒸汽压、冰点和等压摩尔热容等数据的多目标拟合，得到了12组液相特征参数；通过对固液相平衡数据拟合得到了7个固相物种的热力学参数和多温表达式.利用液相特征参数和固相物种参数，对3个二元体系、3个三元体系、1个四元体系物性和多温相图的准确计算，给出了三元和四元体系完整相图的合理预测，适用温度范围为254.65~543.15 K，NaNO3的浓度高达226.88 mol/kg.研究结果拓展了电解质模型在超浓和多温复杂体系的表达能力，模型及参数可用于含硝酸盐体系的化工过程、废水处理和盐湖卤水资源开发等过程.

支持信息见http：//www.cjcu.edu.cn/CN/10.7503/cjcu20210334.