微机械陀螺仪解调相角在线自补偿方法*

丁柏会,贾 佳,李宏生

(1.东南大学 仪器科学与工程学院,江苏 南京 210096； 2.东南大学 微惯性仪表与先进导航技术教育部重点实验室,江苏 南京 210096)

0 引 言

微机械陀螺仪因具有体积小、重量轻、易于批量生产等优点[1,2],在军事和民用领域有着广泛的应用前景。实际应用中为了降低成本,一部分微机械陀螺仪采用常压封装,这类陀螺仪通常具有低品质因数、小频差等特点。

由于加工误差的存在会导致正交刚度误差,此时陀螺仪的输出信号包含正交信号和哥氏信号。大多数解调方法基于相敏解调原理,这要求解调参考信号和预解调信号之间的相位差保持在90°或180°。当微机械陀螺仪具有低品质因数、小频差等特点时,解调参考信号和预解调信号之间会存在较大的相角偏差。若不对解调参考信号进行相位调整,部分正交信号会耦合到哥氏信号路径中[3,4],从而影响陀螺仪性能。针对此问题,文献[5]采用基于幅频和基频曲线的一次性扫频测量陀螺仪测控电路引起的相位延迟。文献[6]介绍了一种基于反向传播(back propogation,BP)神经网络补偿微机械陀螺仪解调相角误差的算法。文献[7]介绍了陀螺仪力再平衡模式下,利用正交回路和哥氏回路输出量与驱动模态相位延迟之间的关系,实现驱动模式下相位延迟补偿。目前解调相角补偿方法补偿效果多依赖于系统输出的重复性,对于输出重复性较差的系统采用该类方法很难对解调相角进行准确补偿。

本文提出了一种基于外部激励信号的解调相角在线自补偿方法,通过在陀螺仪检测模态施加一个远离谐振频率的激励信号在线辨识解调相角,从而对解调参考信号进行相角调整,以减少正交信号对陀螺仪性能的不利影响。

1 解调相角误差对陀螺仪性能影响

微机械陀螺仪分为驱动模态和检测模态,两种模态均可看作“弹簧—质量块—阻尼”二阶系统,考虑模态间耦合,由牛顿第二定律可得微陀螺仪开环检测状态下动力学方程

(1)

x(t)=Axsin(ωdt+φd)

(2)

式中Ax为驱动位移信号幅值；陀螺仪驱动模态一般工作在谐振状态,此时φd=-90°。当陀螺仪有Ωz输入角速度,并考虑模态间耦合,此时哥氏力信号Fc和正交力信号Fq表达式为

(3)

当陀螺仪检测模态工作在开环状态,此时仅考虑Fc与Fq作用,此时检测模态输出位移响应为

y(t)=Acsin(ωdt-φc)+Aqcos(ωdt-φq)

(4)

其中

(5)

检测位移信号经过前端电路,其等效增益为Kequ,此时Y(t)=y(t)Kequ为待解调信号。

数字化陀螺仪测控系统[8,9]应用直接数字频率合成(digital direct synthesis,DDS)技术产生正弦驱动信号,并提供准确的解调基准Vref=sin(ωdt+φ0),其中,φ0为解调信号初相位。陀螺仪检测模态输出信号经过相敏解调和低通滤波环节最终输出为

(6)

理想情况下,φ0=-φc,此时哥氏通道中耦合的正交分量将被完全抑制,这要求解调相角φ0始终跟随φc。由于φc随温度变化而改变,因此很难实现解调相角φ0始终跟随φc,由此产生的解调误差是影响螺仪输出性能的重要因素。

2 解调相角在线自补偿方法

解调相角补偿算法原理如图1所示。

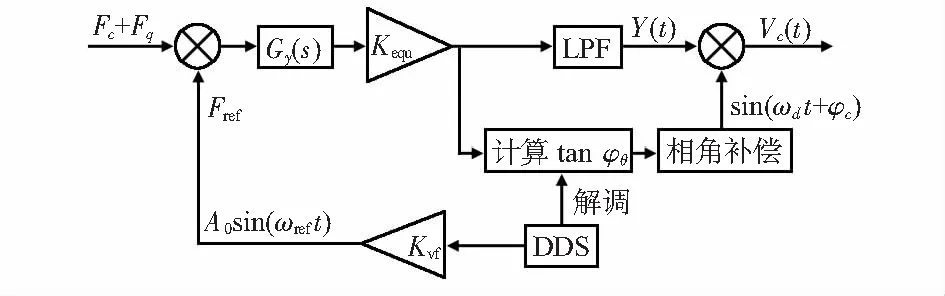
图1 解调相角在线补偿原理

如图,Fref=A0sin(ωreft)为施加在检测力反馈梳齿上的正弦激励信号；其中,ωref=ωd+ωθ为信号角频率,为降低该信号对陀螺仪工作模态的影响,该信号频率应远离陀螺仪谐振频率,设定二者相差500 Hz；Kvf为电压—反馈力转换系数。

相角补偿方法基本思路是通过解调得到激励信号经过陀螺仪检测模态引起的相位延迟φθ,再通过计算得到φc,以下为具体推导过程。

由式(5)可得

(7)

同理,施加在检测模态力反馈梳齿上正弦激励信号Fref=A0sin(ωreft)经过检测模态产生的相位延迟应满足

(8)

结合式(7)和式(8)有

(9)

课题组自研的微机械陀螺仪驱动模态和检测模态谐振频率约为3 500 Hz,两模态间频差Δω≪ωy时式(9)可简化为

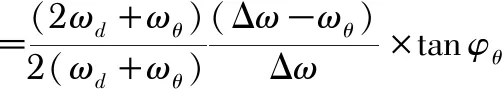
=Ktanφθ

(10)

式中K为补偿系数,是一个与ωd和Δω相关的变量。常温下,#G239表头测量频差以及补偿系数K如图2所示。

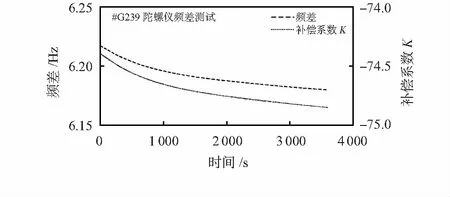
图2 陀螺仪#G239测量频差

如图2可知常温下补偿系数K几乎不变,实际处理时可将K近似为常数,此时可得

φc=arctan(Ktanφθ)

(11)

由上式可得φc，φθ和K三者之间的关系示意图。

如图3所示,解调相角φc与φθ和补偿系数K分别呈非线性关系,当φθ和K小幅度波动,解调相角φc随之变化。

图3 φc，φθ和K关系

基于DDS技术调整正弦信号相位延迟是通过延时若干时钟实现的,陀螺仪数字系统时钟频率为50 MHz,则DDS产生φc相位延迟对应延时时钟数N表达式为

(12)

经过测试,待解调信号与解调参考信号之间相位差由补偿前74°变为补偿后90°,校正了陀螺仪解调相角误差。

3 仿真与实验

3.1 仿真

在MATLAB的SIMULINK仿真工具中建立如图1所示的陀螺仪解调相角在线自补偿模型。设定陀螺仪存在一定的正交耦合误差以及解调相角误差,仿真结果如图4所示。

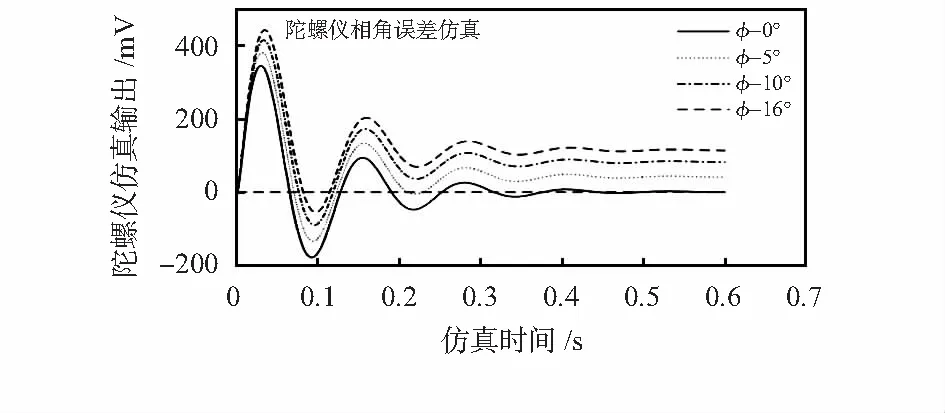
图4 陀螺仪#G239相角误差仿真

从仿真结果可以看出,当陀螺仪存在一定的解调相角误差时,正交信号会“泄露”到哥氏通道,解调相角误差越大,哥氏信号受正交信号影响越大。通过补偿解调相角误差抑制了哥氏信号中的正交信号分量,从而可降低正交信号对哥氏信号的影响。

3.2 实 验

为进一步验证陀螺仪解调相角在线补偿方法的补偿效果,对#G239表头进行试验。陀螺仪及其测控电路如图5所示。

图5 陀螺仪及其测控电路

将微机械陀螺仪固定在测试平台上,常温下测试3 600 s并记录陀螺仪输出,实验重复3次。图6为相角补偿前后实验零偏图。

图6 #G239陀螺仪零偏测试

实验结果可以看出:陀螺仪输出漂移由补偿前的4.9 mV降低到1.3 mV,漂移量下降了73.5 %；同时相角补偿后陀螺仪输出数值明显降低,相角补偿后哥氏信号中的正交信号分量被有效抑制,这与仿真结果一致。表1、表2为相角补偿前后测试结果。

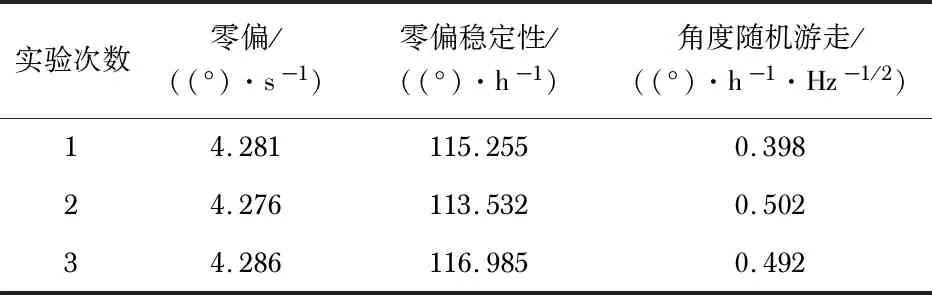
表1 相角未补偿测试

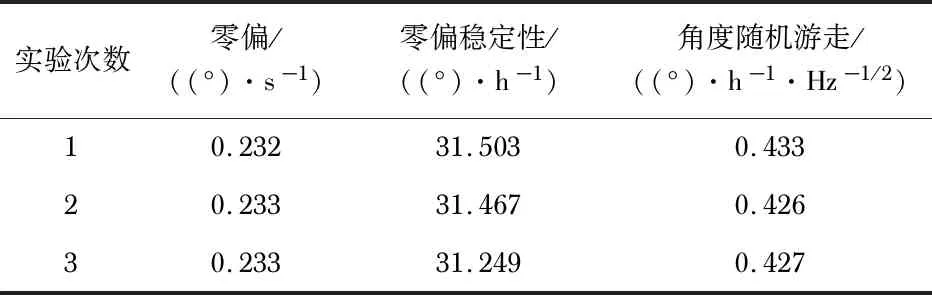
表2 相角补偿测试

陀螺仪#G239零偏稳定性由补偿前115.257°/h降低到补偿后31.406°/h,降幅达到72.7 %。实验结果表明该相角补偿方法可提升具有低品质因数、小频差特点的微机械陀螺仪零偏性能。

4 结 论

本文针对低品质因数、小频差微机械陀螺仪解调相角误差补偿方法进行了研究,提出一种基于外部激励信号的在线自补偿方法。通过理论推导、模型仿真和实验,验证该相角补偿方法可降低正交误差对陀螺仪性能影响,提高常温下陀螺仪的零偏性能。