基于微簇融合的密度峰值聚类算法

2021-10-15宋紫阳刘小康刘传修

传感器与微系统 2021年10期

宋紫阳，张菁，刘小康，刘传修

(上海工程技术大学电子电气工程学院，上海 201620)

0 引言

聚类属于无监督分类，度量根据数据的相似性，将数据划分为不同簇，使得同簇中数据具有较高的相似性，不同簇的数据间具有较大差异性[1]。常见的聚类算法有三种：1)K-means算法属于基于分区的算法，参数设置简单，但该算法存在对聚类中心较为敏感、需要手动设置聚类中心个数和无法辨别噪声点的不足[2,3]；2)BIRCH算法属于层次划分，聚类结果与数据输入顺序有关[4]；3)STING算法作为基于网格划分算法，将空间划分为不同的网格单元[5]，效果取决于网格的最低力度，太大或者太小都无法识别[6]。

基于密度的聚类算法属于典型非参数型算法，其样本点的分布具有某种概率[7]。Rodriguez A和Laio A[8]开发了一种密度峰值聚类(density peak clustering,DPC)算法，该算法可以根据决策图确定聚类中心并检测非球形聚类，而无需指定聚类数。文献[9]认为DPC算法的参数计算过于简单，忽略数据间的相关性，并在高维数据表现结果不佳，对此提出了ADPC-FLD算法，该算法引入皮尔逊相关系数来计算ρi和δi，采用Fisher对数据进行降维处理。文献[10]认为DPC算法过于依赖ρi和δi，存在参数选择的问题，提出了一种基于GSA的混合聚类方法(GSA-DPC)，改进了截止距离的选择机制，提高聚类精度，并基于GSA框架设计了优化聚类中心的方法，采用遗传算法(GA)寻优。文献[11]认为当簇中含有多个密度峰时，DPC算法易将一个簇分为多个簇，提出一种基于支持向量机的新型合并策略(FDPC)，利用支持向量机(SVM)计算每个聚类结果之间的反馈值，并根据反馈值进行微簇合并。

DPC算法在处理稀疏簇和密集簇时无法高效地找到聚类中心，在数据融合方面容错性差。因此,本文提出一种新的聚类方法，即微簇可融合的密度峰值聚类算法。首先,重新定义了局部密度ρi计算公式，其次将融合策略与DPC算法结合，最后引入非负分解(NMF)算法，对高维数据进行降维，提高算法的鲁棒性能。通过不同的数据集进行实验，证明了本文改进算法在处理不同形状簇的有效性。

1 DPC算法

DPC算法2014年发表在《Nature》上[12]，具有不需迭代、参数设置少及等快速找到聚类中心等特点，近年来其衍生的相关算法迅速发展。DPC算法的核心思想为：对于每个采样点，首先计算两个变量，即局部密度ρi和到邻近最大密度δi的距离，然后每个采样点xi∈X，X={x1,x2,…,xn}，局部密度ρi定义为

(1)

(2)

式中dij为数据点xi与数据点xj之间的距离，dc为截止距离。

到邻近最大密度δi的距离定义为

(3)

对于具有高局部或全局密度的样本点，没有高密度的最近邻，并且距离最近的较大密度点的距离简单描述为

(4)

具有ρi和δi，以γ作为选择聚类中心的指标，γ的计算公式为

γ=ρδ

(5)

2 MCF-DPC算法

2.1 改进的局部密度计算公式

K最近邻(KNN)常用于分类、聚类等邻域测量中[13]，给定数据点i，其knn(i)可表示为

knn(i)={j|dij≤di,kth(i)}

(6)

式中dij为i到j之间的欧氏距离，kth(i)为i的第k个邻域。

本文根据KNN算法的思想定义一些MCF-DPC算法使用的概念，如下：

定义1 累计最近邻度βk(i)

(7)

式中knn(i)为数据点i的k邻域集合。

定义2 离心率φi

(8)

定义3 基于k邻域的局部密度ρi

(9)

2.2 融合策略

传统DPC算法对于数据聚合根据ρi和δi决定的决策图选择前几个γ值大的点作为聚类中心，这种方案在处理同时具有密集和稀疏形状的数据集时，算法的容错性差，某一点的分配错误，带来的影响将会被放大，严重影响聚类效果。因此本文提出了一种新的融合策略——微簇融合(micro-cluster fusion,MCF)。

定义4 数据加权内平均距离α

(10)

定义5 簇间密度差CD

(11)

定义6 簇间距离CB

CB=min(d(ri,rj))

(12)

式中n为数据维度，αij为数据点i到j的加权内平均距离。A和B为两个微簇，ri和rj分别为A和B内的点，d(ri,rj)为ri和rj的距离。MCF可表示为

MCF(A,B)=CB·CD2

(13)

MCF(A,B)的值越大，说明微簇间差异性越大;反之，说明簇间相似性很大，可以进行微簇融合。对此需要设置一个阈值作为衡量簇间相似性的标准。通过实验发现当MCF(A,B)小于阈值时，进行微簇融合聚类效果较佳。设阈值为所有数据MCF的平均值的1/5，即0.2×avg(MCF)时。微簇融合策略主要步骤如算法1。

输入：处理后数据及聚类中心

输出：聚类结果

1)按式(10)计算数据加权平均距离

2)按式(11)计算簇间密度差

3)按式(12)计算簇间距离

4)判断MCF(A,B)是否小于阈值，符合则进行簇间融合

由表3可以看出，对于B分量图像：面积在190～250之间的鸡蛋，蛋黄指数大于0.72则判定为双黄鸡蛋；面积小于190的鸡蛋，蛋黄指数的大于0.84则判定为双黄鸡蛋。

5)输出聚类结果

2.3 非负矩阵分解

NMF由Lee和Seung在2000年提出的基于特征变换的数据降维方法[14]。NMF的思想：给定要分解的非负矩阵X(m*n)，计算满足以下表达式的非负矩阵B(m*r)和H(r*n)

X≈B*H

(14)

式中矩阵B称为基矩阵，H称为系数矩阵。参数r表示矩阵分解的秩，且小于m和n

(15)

minE(B,H),B>0,H>0

(16)

用梯度下降法求解目标函数，公式如下

(17)

数据降维主要步骤如算法2。

算法2数据降维算法

输入：高维数据集X={x1,x2,…,xn}，n为样本数

输出：低维数据集Y={y1,y2,…,yn}

1)输入原始矩阵X

2)设置迭代次数k

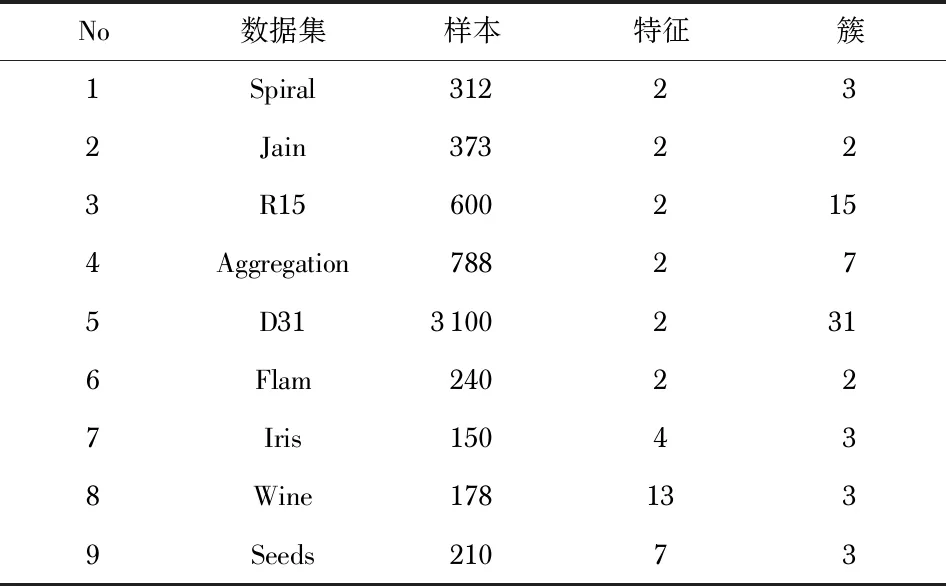
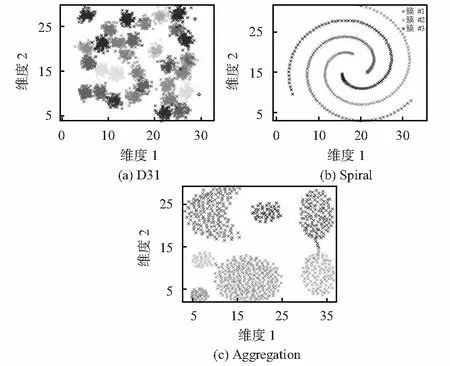
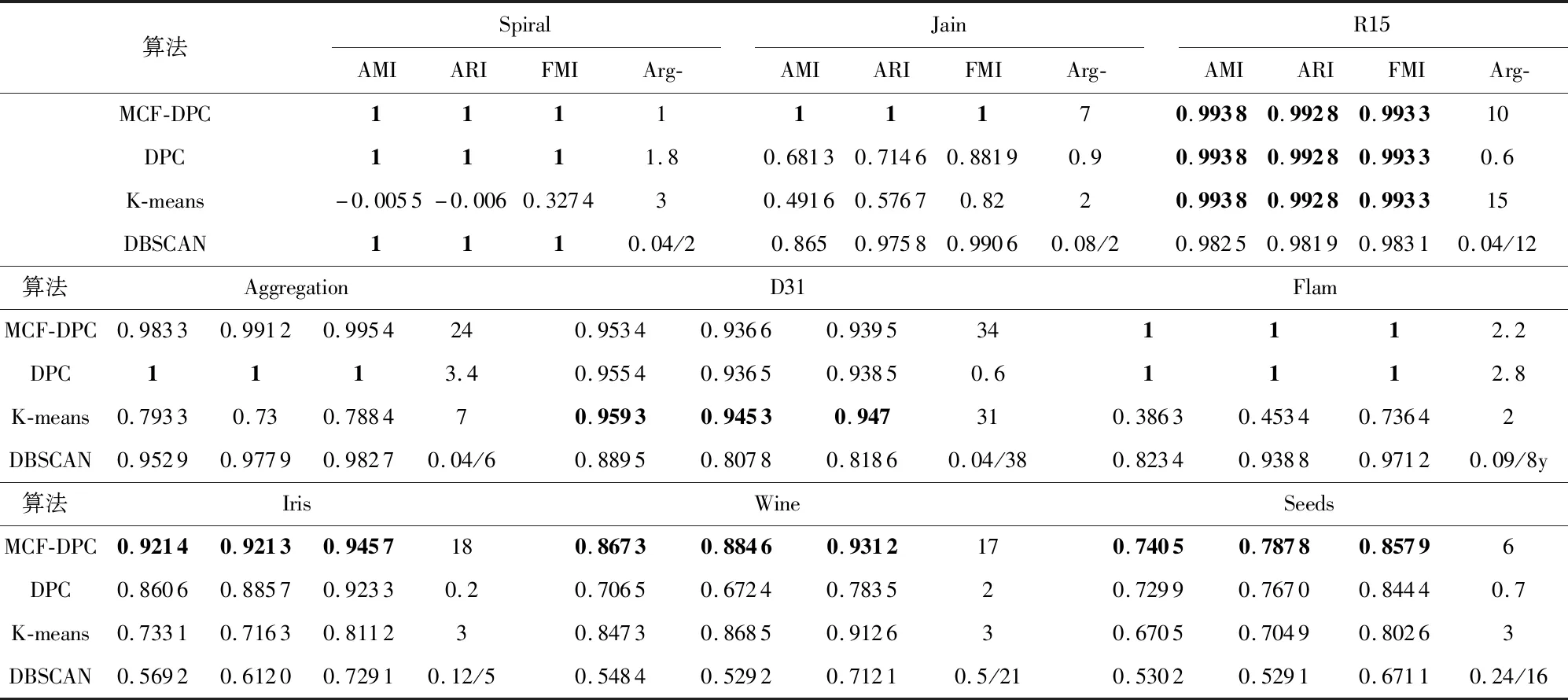
fort

end for

3)输出Y=H

2.4 算法流程

MCF-DPC算法主要步骤如算法3所示。

算法3 MCF-DPC算法

输入：数据集X={x1,x2,…,xn}，n为样本数

输出：聚类结果

1)调用算法2，获得数据的系数矩阵H

2)计算距离矩阵dij

3)根据式(8)计算ρi，根据式(3)和式(4)计算δi

4)由式(5)计算γi，绘制决策图并选择聚类中心

5)将其他数据分配给聚类中心

6)删除噪声数据和异常值

7)按照算法1进行微簇融合

8)输出聚类结果

3 实验结果与分析

选取9个数据集，将本文所提的MCF-DPC算法与传统的DPC算法、K-means以及DBSCAN算法进行比较，9个数据集具体参数如表1所示。

表1 6个合成数据集参数

K-means算法和DBSCAN算法具体参数均根据文献[15]设置。部分MCF-DPC的聚类结果如图1所示，各算法在不同数据集详细的性能指标如表2。

图1 MCF-DPC的聚类结果

表2 各聚类算法在不同数据集上的性能

表2所示的五种算法在所有综合数据集上得分，最佳得分以粗体显示。从表2中，可以看出该算法在大多数综合数据集上的表现很好。MCF-DPC算法在7个数据集上表现最佳，在Jain，Iris，Wine和Seeds数据集上MCF-DPC算法是表现最佳的唯一算法。在Spiral数据集上除K-means算法外均能取得不错的效果，可见对于简单的螺旋状的Spiral算法的参数设置对聚类结果影响不大。本文提出的微簇融合机制对聚类具有良好容错性。