研究生入学考试中行列式的计算一例

刘海峰，李雪莹

(上海海洋大学 信息学院，上海 201306)

线性代数是大学理工科各专业的一门数学基础课，也是全国硕士研究生入学考试中数学(一)、数学(二)和数学(三)试题中必考的内容，其重要性不言而喻。同时，线性代数因其概念的抽象一直是本科生普遍认为比较难学的一门课[1]。怎样才能学好线性代数呢？童增祥教授在文献[2]中强调，大学生“要学好数学，必须做大量的题目”，遇到困难要“多思考，寻求一种或多种解题方法”。文献[3]也指出一题多解是线性代数教学中培养学生创新思维的途径。本文以一道考研题目为例，从不同的观察角度出发，利用线性代数不同部分的知识给出4种解法，希望能给学习线性代数的同学一点启发。

2020年全国硕士研究生入学考试数学(一)试卷的第13题(同时是数学(二)的第14题，数学(三)的第13题)如例1所示。

首先想到的解法就是将行列式按某行(或某列)展开[4]74，而在此之前往往要对行列式作一些初等变换。

解法1降阶法，即按行列式的某一列(或行)展开。

先做行变换。将第4行加至第3行，第4行的-a倍加至第1行，然后按行列式的第1列展开，得

(1)

将式(1)中三阶行列式的第1行减去第2行，并按第1列展开，可得

所以，行列式的值是a×(-2a-a×(2-a2))=a4-4a2。

以上是最直接的做法。然而注意到该行列式的特殊性，还可以得到下面的几种巧妙的解法。这些求解办法体现了行列式与有关概念之间的深刻联系。

解法2利用行列式的定义及偶函数的性质。

由行列式的原初定义不难得知该行列式为a的4次多项式，且首项的系数为1。若记为f(a),可证其为偶函数。为此，先将f(-a)的前两行各乘以-1，再将后两列各乘以-1,立即可知

因此，不妨设f(a)=a4+λa2+μ，再用待定系数法确定λ,μ即可。事实上，由a=0时行列式为0立即可得μ=0,再由a=1时行列式为-3可得λ=-4。所以，f(a)=a4-4a2。

解法3利用分块矩阵的性质。

在此例中，由A,B的定义可知

|C|=|A-BA-1B||A|=a2(a2-4)。

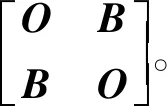
总之，无论a是否为零，均有|C|=a2(a2-4)成立。

注：当a≠0时，还可以用另外一种方法计算该行列式。因为A是数量矩阵，所以它与B的乘积可交换，即BA=AB，于是有

|C|=|A-BA-1B||A|=|(A-BA-1B)A|=|A2-B2|。

由A2=a2E及B2=-2B立即可得

解法4利用特征值和特征多项式的关系。

由于a=0是f(a)的特征根，且不难观察到向量ξ1=(1，1，0，0)T和ξ2=(0，0，1，1)Τ是D的属于特征值0的两个线性无关的特征向量，所以0是二重特征根。又注意到ξ3=(1，-1，1，-1)Τ是D的属于特征值2的一个特征向量，以及矩阵D的迹为零，由实对称方阵的迹等于其特征值之和可知，-2必是f(a)的另一个非零特征根。最后，由特征多项式的首项系数为1即知D的特征多项式为

f(a)=a2(a-2)(a+2)=a4-4a2。

一般来说，解题时观察问题的角度决定了解决问题所使用方法和理论工具，继而决定了解答过程的难易程度和答题步骤的复杂程度。以上4种解法分别涉及了行列式按行(或列)的展开定理、行列式的定义、分块矩阵、方阵的逆、迹、特征多项式和特征值、特征向量以及函数的奇偶性等诸多概念和相关的结论。解法3和解法1看似不同，但本质上都是降阶[7]。

在实际考试答题的过程中，考生不一定能在有限的时间内给出多种解题方法。但是在日常学习过程中应养成用一种方法解答，再尽量用另外一种方法加以验证的习惯，这对理解线性代数概念之间的深刻联系、培养创新思维是非常有益的。虽然文中的各种解法不尽相同，但最终计算的结果相同，这既体现了线性代数各部分内容的统一性，也表明了行列式在线性代数中的基本重要性。