一种改进的中文字符矢量化算法
2021-10-15李新杰江子傲王存睿
李新杰,江子傲,王存睿
(大连民族大学 计算机科学与工程学院,辽宁 大连 116605)
字体作为传递信息的关键载体,在计算机显示中也是必不可少的,字体技术从最开始的点阵字库、矢量字库发展到了曲线字库[1-2]。字体矢量化需要经历样字扫描得到简单的矢量轮廓,然后人工去判断向量轮廓上的每个向量点是曲线还是直线上的点,还需要判断连续的向量段是用一条直线还是用曲线逼近。GBK字库有两万余字,这些字都由人工进行矢量化,是一个工作量十分浩大的系统工程[3]。这种人工修改得到曲线字,生产效率较低,因此研究自动将字体图像转为曲线字形的矢量化方法具有十分重要的现实意义。
1 图像矢量化算法研究现状
曲线字形因为其锚点少,占用空间小,在计算机中加载速度快,例如,Plass和Stone在1983年使用分段参数三次多项式来表示位图点序列[4];Agarwal等人在2005年介绍了一种近似线性时间复杂度下的曲线简化算法;Kolesnikov和Franty在2007年提出了一种求闭合曲线多边形逼近的算法[5]。经典的位图轮廓矢量化算法Potrace[6],它利用多边形逼近的方法,可以高效的完成位图的矢量化工作。但是,只有在位图的分辨率较高的情况下,选取的锚点较为准确,当位图分辨率不高时,矢量化过程中选取的锚点就会出现不准确和冗余的情况。
在进行字体图像矢量化时得到的字形轮廓中含有大量的冗余点,没有对字形轮廓中的点集做筛选。对于算法生成的字形轮廓无法定量的分析其质量地优劣,只能人工大概地去判断关键点选的是否准确、形状是否与原稿吻合。
为了全面地检测和度量本文所提到的矢量化方法的效果,本文从轮廓尖锐度[7]、关键点冗余率、锚点准确度[8]以及形状吻合度[9]等四个方面提出了相关的度量指标,并分别建立了其对应的检测方法。
对于轮廓平滑的正文字体图像,本文在基于经典的Potrace位图矢量化方法的基础上进行改进,增加了消除冗余点的过程,形成了一套针对正文字体的矢量化算法。
2 改进的Potrace字体图像矢量化方法
对于Potrace方法的优化和改进主要集中在对关键点冗余率的降低上,对于选出的最优多边形,对其进行去除冗余点的操作。详细算法流程如图1,算法步骤主要分为如下六步。
Step1: 根据夹角判别法筛选出“可疑”冗余点,得到“可疑”点集;
Step2: 计算每个“可疑”冗余点的“删除代价”(DC)值,剔除小于阈值TDC的点,保留“删除代价”较大的点;
Step3: 检测冗余率是否达标,是则继续下一步,否则调整夹角阈值和删除代价阈值,然后返回Step 1;
Step4: 根据弧弦距判别法判断矢量段的拟合类型,决定保留多边形的直线段还是用贝塞尔曲线插值拟合;
Step5: Bezier曲线插值拟合关键点;
Step6: 合并优化Bezier曲线段。
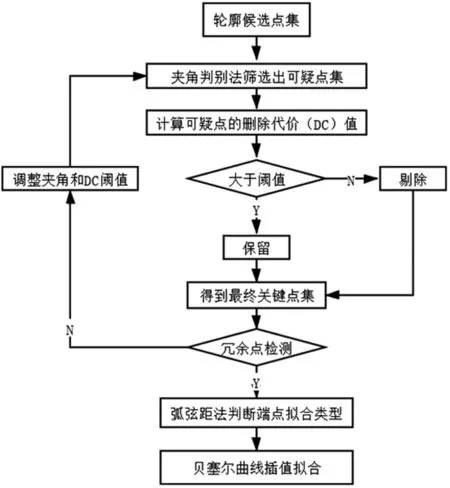
图1 改进部分的算法流程图
2.1 初步筛选“可疑”冗余点集
本文提出了夹角判别法来初步筛选冗余点,基本原理为:首先取环上邻近三点作为一个单元,分析夹角,若夹角小于阈值,则作为规范关键点保留,继续遍历;若夹角大于阈值,则加入到“可疑”冗余点列表。具体的定义和计算步骤如下。
以Potrace算法所得到的多边形顶点集P为初始集合,定义集合D为它的“可疑”点集,遍历初始点集,设Pi为点集中的一点,其相邻点为Pi-1和Pi+1,则由Pi,Pi+1和Pi+1三点可构成一个三角形,由余弦定理可求出以Pi为角心的角度值 α,其中
(1)
某笔画局部轮廓点集如图2。这里取夹角角度阈值 Tang=172,则夹角角度大于172的点将被加入到“可疑”冗余点集;例如B点夹角∠ABC=121,所以 B 点为必然关键点,排除冗余的可能;由于C点夹角∠BCD=175,大于Tang,所以 C 点为可疑冗余点;同理,D、E 和 I 点的角度均小于阈值,为必然关键点,而 F、G、H 和 K 点的角度大于阈值172,故需要加入到“可疑”点集中。
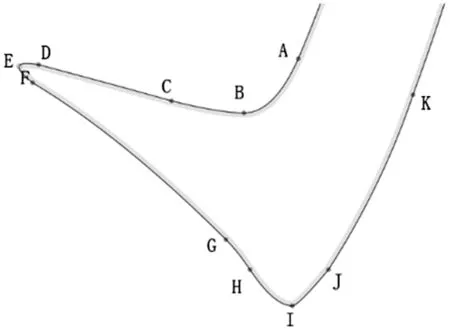
图2 某笔画局部轮廓点集
2.2 确定冗余点集
在得到可疑的冗余点集 D 后,是否能将其从初始点集 P 中删除,还要取决于其删除后对整个轮廓的影响,这里本文定义了一个变量“删除代价”(Delete Cost, DC)来决定该可疑点是否真正的冗余且可被删除。
DC 值用于测量删除每个轮廓点的成本。在本方法中做出规定:移除后对拟合结果影响最小的点将被逐个删除。首先对多边形点集中的所有点进行遍历,然后遇到“可疑”冗余点后,计算其删除代价 DC 值,若大于设定阈值保留该点不予删除;小于阈值则确定为冗余点,并将其删除。

Dk=max{ym-xm│m∈(i,j)。
(2)
即Pk的“删除代价”定义为影响值Vm的最大值,其中Pm是它的两个相邻显著点Pi和Pj之间的轮廓点。最后,调整阈值TDC,如果小于TDC,则认为Pk是冗余的关键点,应该去掉,否则保留。
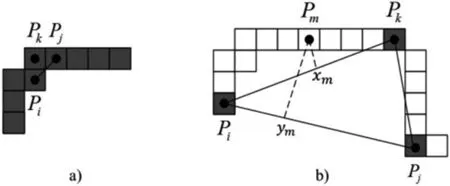
图3 删除代价原理图
2.3 判断拟合类型
至此已经得到了冗余率检测能够达标的关键点集,然而由于Potrace方法在拟合阶段将所有多边形的边线段都用贝塞尔曲线进行拟合,曲线片段过多会导致控制点过多,这里本文加入了弧弦距的方法[10]能够保留一定的直线片段,从而降低贝塞尔曲线的控制点的数量。
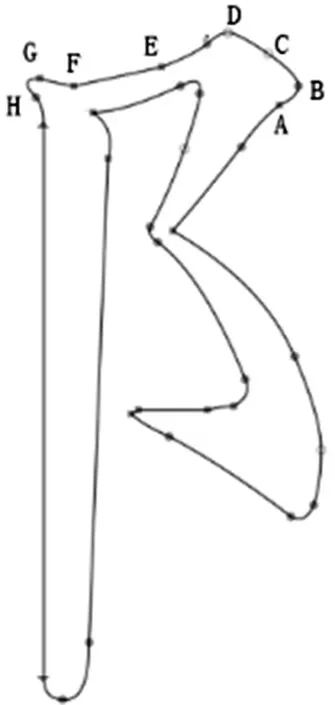
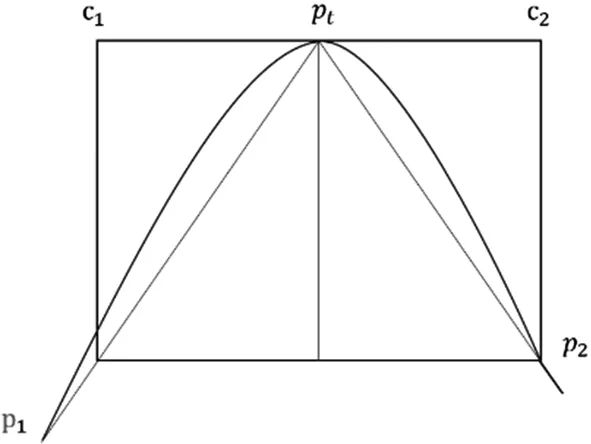
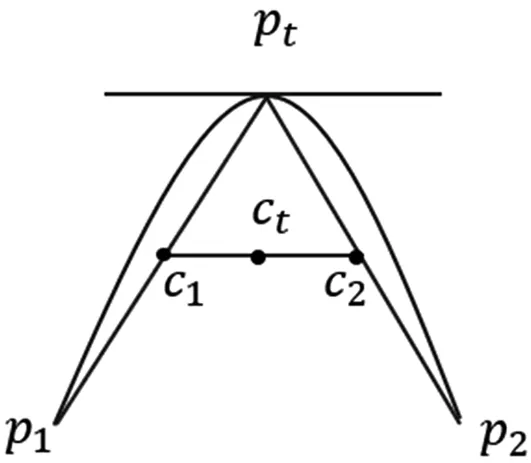
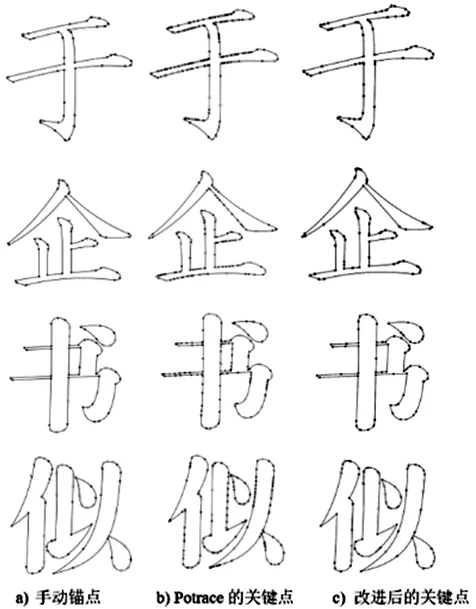
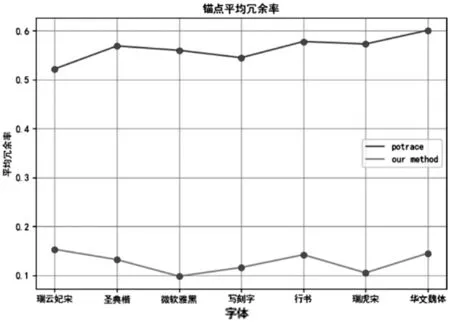
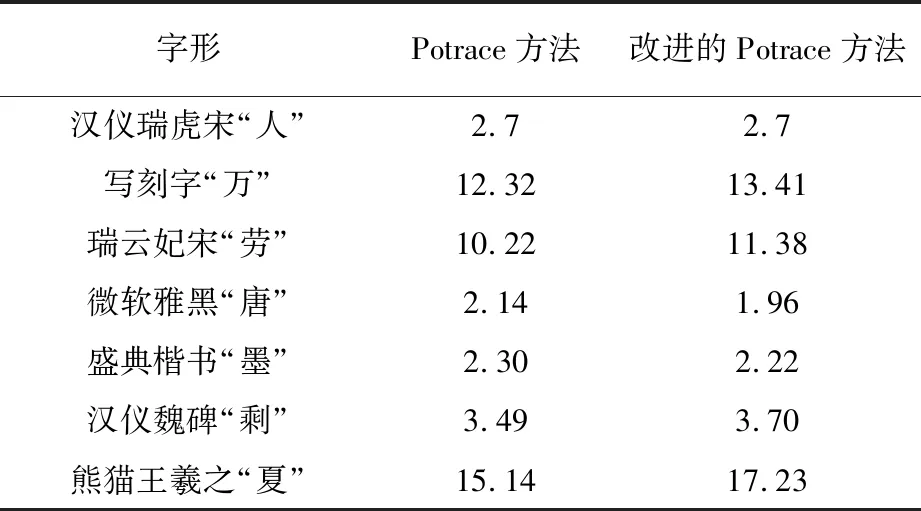
所谓弧弦距,就是矢量段上的点到连接矢量段两端点所成的弦的最大距离;所谓基准弧弦距原则,就是预先给定一个弧弦距值作为基准,来判断某矢量段是用直线段还是用曲线段来替换;对多边形上连续的矢量段,根据基准弧弦距原则进行判断,确定矢量段的替换类型如图4。 由图4可以看出连接矢量段 AB 的两端点的弦为线段 AB,矢量段AB上C点到线段AB的距离最大,记为d,则d就称为矢量段 AB 的弧弦距。根据拟合精度的需要,设定一个数值 T 作为判断矢量段 AB 应该用直线段还是曲线段代替的基准,如果d 图4 弧弦距示意图 应用于处理矢量字形轮廓如图5。使用Potrace方法提取的关键点为 A、B、C、D、E、F、G、H 等,设定基准弧弦距 T 为0.8,根据基准弧弦距原则判定两两关键点间的矢量段的替换类型。矢量段AB的弧弦距为1.2,大于预先设定的基准T,则矢量段 AB 应该用曲线段替换,从而存储矢量段 AB 的线段类型标志为“2”,并存储A点坐标,同理存储 BC、CD、DE;矢量段 EF 的弧弦距为0.5,小于基准 T,则应用直线段替换,从而存储线段类型标志为“1”,并顺次存储 E 点和 F 点坐标;同理处理矢量字形轮廓上的其他矢量段。这样将得到的待插值拟合的直线端点和曲线端点按字形轮廓数据的存储格式保存,最终生成曲线字轮廓数据表示。 图5 根据弧弦距判断向量段拟合类型 字符轮廓线由直线和曲线组成[11],因此,如果在两个相邻的锚点之间的轮廓线是直线,则遍历轮廓中的锚点以逐段拟合轮廓线时,不需要控制点和线性Bezier曲线即可拟合。如果在两个相邻的锚点之间存在曲线,则将出现两种情况, 一种是下一个轮廓仍然是一条曲线(即两条连续的平滑曲线),另一种是下一个轮廓是一条直线。为了简化算法,可以在第二种情况下在曲线段的中间添加锚点,以在第一种情况下对其进行变换。因此,这里只需要将两条连续的平滑轮廓曲线与两条二次贝塞尔曲线拟合即可。 由于字体曲线的轮廓线是平滑的,因此在将长曲线轮廓用多段Bezier曲线拟合时,必须使每个Bezier曲线的连接平滑。可以看出,贝塞尔曲线的控制点和锚点之间的连接与贝塞尔曲线本身相切如图6。假设控制点 c1、c2和两段贝塞尔曲线连接处的锚点 pt共线,可以确定两条Bezier曲线的交点是平滑的。因此,该思想可用于计算贝塞尔曲线的控制点。 图6 角平分线法拟合轮廓 计算控制点的方法如图7。取直线为平分线的垂线,令 c2暂为 p2在上的投影,且与等长,然后,对 c1和 c2缩放,通常实际控制点在原始投影点的0.2到0.6之间。最后,计算由缩放控制点和相应的锚点所绘制的贝塞尔曲线与原曲线所包围的封闭空间的面积[12],并使用面积更小且更接近0的缩放点作为最终检查点。从逻辑上讲,该区域可能不接近0,因此将不接近0的曲线再次划分,并重复先前的计算。鉴于上述方法,当控制点不在相邻锚点的线段等分线的垂直线上时,有必要将曲线分割并添加锚点以达到拟合的目的。下面补充实现轮廓拟合的第二种方法,此方法类似于先前的方法,需要两条连续的平滑曲线。 图7 中点法拟合轮廓 在上一节中已经得到了由多段贝塞尔曲线拟合的矢量字符轮廓线,虽然它己经很好地拟合了字符轮廓线,但其锚点和控制点数一般还是比较多,仍需要对其进行优化,即合并相邻的贝塞尔曲线段。在此,不合并直线段和曲线段,而只合并满足条件的连续曲线段和连续直线段。 这里的条件是由合并的贝塞尔曲线和原始轮廓曲线形成的封闭空间的面积接近于零。连续曲线合并的方法如图8。合并相邻的两段曲线 b0b1和 b1b2,只需延长 b0a1和 b2a2,其相交于一点则为合成后贝塞尔曲线的控制点,否则不能合并。如果验证了此新合并的贝塞尔曲线满足条件,那么就以此段曲线为第一段曲线迭代上面操作,否则此处不能合并。 图8 连续曲线合并原理图 本文抽取了几种常用的商用字库,然后对其图像进行矢量化操作,由于本章节主要讨论的是对正文字体图像的矢量化,正文字体轮廓本身就是平滑的,而Potrace算法对于轮廓本身比较平滑的字体矢量化后轮廓依然可以保持原来的平滑程度,故这里不再对尖锐度这个指标进行检测对比,接下来将就锚点冗余率、关键点的准确度和形状吻合度等三项指标分别进行检测,然后对Potrace方法及其改进后的方法进行对比实验,并对结果进行分析。最后为了进一步说明本改进方法对于曲线字库的重要性和优越性,还展示了一项关于字库的重要检测指标,即字库的空间压缩比。 锚点即关键点如图9。这一项指标是所有检测指标中最为关键的一项,直接决定着矢量字体的质量,想要达到的预期实验结果是用最少的点就能描绘字形,即锚点的冗余率越少,则认为该算法的锚点效果越好。本文从7个商用字库中各选取了9 169个汉字作为实验变量,按照笔画由少到多的字形分别对其用包括手动锚点在内的三种方法进行锚点,部分实验结果见表1。不同字库的锚点平均冗余率如图10。 图9 轮廓关键点对比实验图 表1 轮廓锚点实验部分数据结果 通过实验数据发现,随着检测字体数量的增多,轮廓锚点冗余率逐渐趋于稳定,Potrace算法的冗余率大约在56%左右,而本文的算法则将冗余率降到10%左右。经过分析可知,在本文针对Potrace方法的改进中,根据夹角阈值选出的“可疑点”能够筛选出大量的冗余点,10%的点冗余是由于删除代价的阈值决定的,若该阈值设置得过大,则会导致有些关键点被“误删”,所以10%的冗余率是符合标准的。 图10 不同字体锚点冗余率对比图 这里同样采用上述7×916 9个实验字体,以设计师手动锚点生成的svg矢量图读取的控制点和关键点为参照点集,分别计算其Hausdorff距离[8],为了控制变量,这里统一选择位图像素为512×512,实验结果见表2。不同字体轮廓点集平均偏差值对比图如图11。可以看出,同一分辨率下,轮廓复杂度越高的字体,算法改进前和改进后的Hausdorff距离都很大,即锚点的准确度都会降低,但本文去除冗余点后的方法的偏差值明显要低于Potrace算法,说明本文对于Potrace算法的改进是有效且可行的。 表2 部分字体轮廓点集的Hausdorff距离 图11 不同字体轮廓点集平均偏差值对比图 由于本文改进的算法降低了Potrace算法得到的多边形的冗余率,但是在去除冗余点后字体轮廓的形状是否发生了改变,也是需要检测的一项指标,所以这里用是 dHashValue 值来检测其形状吻合度,dHashValue 越大则形变越大[9],由于Potrace方法对于拟合形状已经很精准,那么这里衡量的一项标准在于改进后的结果的 dHashValue 值是否与Potrace方法接近,接近则说明本文方法可以在去除冗余点后还是能够很精准的拟合字形的轮廓。部分字体的实验数据见表3。不同字体轮廓的平均dHashValue值对比图如图12。虽然在字形轮廓较复杂时 dHashValue 较大,但是基本上可以看出改进后的方法和改进前的差值并不大,即对字形轮廓的拟合形状还原度还是比较高的,图12进一步反应了这一点,也进一步说明改进方法是有效且可行。 表3 两种方法对于部分字形的 dHashValue 图12 不同字体轮廓的平均dHashValue值对比图 单个字形去除冗余点的空间抽稀效果还不明显,真正能反应冗余点去除之后的效果还是要在整体字库的层面上,因为只有整个曲线字库的空间存储量更小,加载速度才能更快,为了进一步证明改进算法的实际作用,这里为字库再定义一个指标,称为字库的空间压缩比。接下来对选取的七种典型字库(每种字体包含9 169个常用汉字)进行矢量化实验,并分别统计其TrueType字库文件的空间大小[13],其中采用的原始字体位图大小为512×512像素,每种字体的9 169张位图所占空间大小均为1536 MB,对应两种方法生成的TTF字库格式文件大小统计结果如图13。由统计结果可看出,本文改进后的方法对于曲线字库文件的空间压缩比是相当低的,即压缩效果达到了预期效果,特别是对于“写刻字”这类轮廓复杂的字体,压缩效果尤其明显。 本文提出了一种根据Potrace改进后的字体图像矢量化方法,并且建立了字体曲线轮廓的度量指标,其中包括轮廓尖锐度、关键点冗余率、锚点准确度和形状吻合度等指标。在使用本文提出的方法进行实验发现得到的字形轮廓质量优于原Potrace算法,也论证了本文方法的有效性和可行性。在矢量化的过程中虽然在关键点和字形上能够达到预期效果,但是针对算法本身来说,由于其对多边形点集进行了多次遍历,时间复杂度较高,降低字体矢量化算法的时间复杂度是一个需要解决的问题,同时根据字体设计的美学原理建立起一套完整的规范体系也是一个值得研究的方向。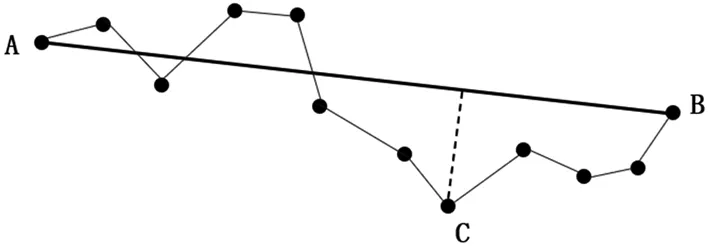
2.4 实现轮廓拟合
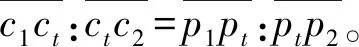
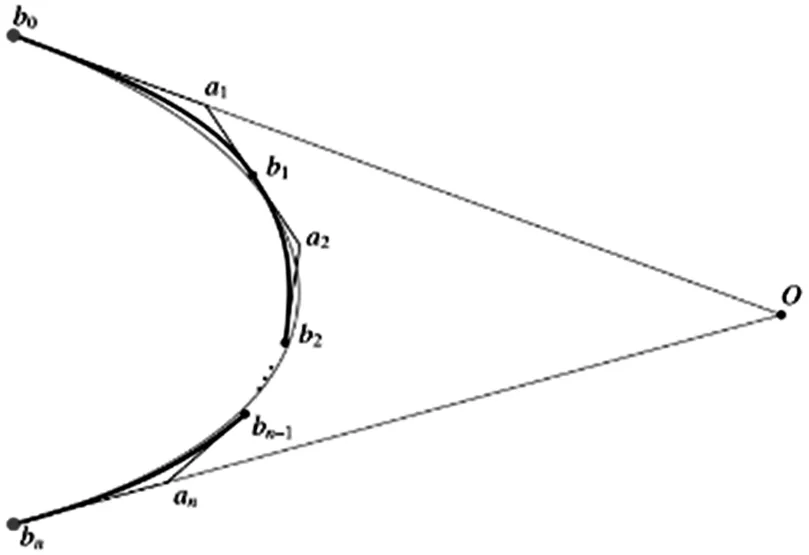
2.5 贝塞尔曲线合并与优化
3 实验结果与分析
3.1 关键点冗余率的对比

3.2 锚点准确度的对比


3.3 形状吻合度的对比

3.4 空间存储压缩比的对比
4 结 语
